Lecture 5: Overdispersion in Logistic Regression
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

An Introduction to Poisson Regression Russ Lavery, K&L Consulting Services, King of Prussia, PA, U.S.A
NESUG 2010 Statistics and Analysis An Animated Guide: An Introduction To Poisson Regression Russ Lavery, K&L Consulting Services, King of Prussia, PA, U.S.A. ABSTRACT: This paper will be a brief introduction to Poisson regression (theory, steps to be followed, complications and interpretation) via a worked example. It is hoped that this will increase motivation towards learning this useful statistical technique. INTRODUCTION: Poisson regression is available in SAS through the GENMOD procedure (generalized modeling). It is appropriate when: 1) the process that generates the conditional Y distributions would, theoretically, be expected to be a Poisson random process and 2) when there is no evidence of overdispersion and 3) when the mean of the marginal distribution is less than ten (preferably less than five and ideally close to one). THE POISSON DISTRIBUTION: The Poison distribution is a discrete Percent of observations where the random variable X is expected distribution and is appropriate for to have the value x, given that the Poisson distribution has a mean modeling counts of observations. of λ= P(X=x, λ ) = (e - λ * λ X) / X! Counts are observed cases, like the 0.4 count of measles cases in cities. You λ can simply model counts if all data 0.35 were collected in the same measuring 0.3 unit (e.g. the same number of days or 0.3 0.5 0.8 same number of square feet). 0.25 λ 1 0.2 3 You can use the Poisson Distribution = 5 for modeling rates (rates are counts 0.15 20 per unit) if the units of collection were 8 different. -

Overdispersion, and How to Deal with It in R and JAGS (Requires R-Packages AER, Coda, Lme4, R2jags, Dharma/Devtools) Carsten F
Overdispersion, and how to deal with it in R and JAGS (requires R-packages AER, coda, lme4, R2jags, DHARMa/devtools) Carsten F. Dormann 07 December, 2016 Contents 1 Introduction: what is overdispersion? 1 2 Recognising (and testing for) overdispersion 1 3 “Fixing” overdispersion 5 3.1 Quasi-families . .5 3.2 Different distribution (here: negative binomial) . .6 3.3 Observation-level random effects (OLRE) . .8 4 Overdispersion in JAGS 12 1 Introduction: what is overdispersion? Overdispersion describes the observation that variation is higher than would be expected. Some distributions do not have a parameter to fit variability of the observation. For example, the normal distribution does that through the parameter σ (i.e. the standard deviation of the model), which is constant in a typical regression. In contrast, the Poisson distribution has no such parameter, and in fact the variance increases with the mean (i.e. the variance and the mean have the same value). In this latter case, for an expected value of E(y) = 5, we also expect that the variance of observed data points is 5. But what if it is not? What if the observed variance is much higher, i.e. if the data are overdispersed? (Note that it could also be lower, underdispersed. This is less often the case, and not all approaches below allow for modelling underdispersion, but some do.) Overdispersion arises in different ways, most commonly through “clumping”. Imagine the number of seedlings in a forest plot. Depending on the distance to the source tree, there may be many (hundreds) or none. The same goes for shooting stars: either the sky is empty, or littered with shooting stars. -

Poisson Versus Negative Binomial Regression
Handling Count Data The Negative Binomial Distribution Other Applications and Analysis in R References Poisson versus Negative Binomial Regression Randall Reese Utah State University [email protected] February 29, 2016 Randall Reese Poisson and Neg. Binom Handling Count Data The Negative Binomial Distribution Other Applications and Analysis in R References Overview 1 Handling Count Data ADEM Overdispersion 2 The Negative Binomial Distribution Foundations of Negative Binomial Distribution Basic Properties of the Negative Binomial Distribution Fitting the Negative Binomial Model 3 Other Applications and Analysis in R 4 References Randall Reese Poisson and Neg. Binom Handling Count Data The Negative Binomial Distribution ADEM Other Applications and Analysis in R Overdispersion References Count Data Randall Reese Poisson and Neg. Binom Handling Count Data The Negative Binomial Distribution ADEM Other Applications and Analysis in R Overdispersion References Count Data Data whose values come from Z≥0, the non-negative integers. Classic example is deaths in the Prussian army per year by horse kick (Bortkiewicz) Example 2 of Notes 5. (Number of successful \attempts"). Randall Reese Poisson and Neg. Binom Handling Count Data The Negative Binomial Distribution ADEM Other Applications and Analysis in R Overdispersion References Poisson Distribution Support is the non-negative integers. (Count data). Described by a single parameter λ > 0. When Y ∼ Poisson(λ), then E(Y ) = Var(Y ) = λ Randall Reese Poisson and Neg. Binom Handling Count Data The Negative Binomial Distribution ADEM Other Applications and Analysis in R Overdispersion References Acute Disseminated Encephalomyelitis Acute Disseminated Encephalomyelitis (ADEM) is a neurological, immune disorder in which widespread inflammation of the brain and spinal cord damages tissue known as white matter. -
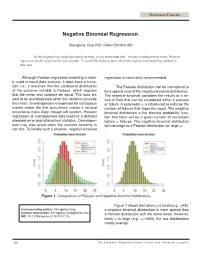
Negative Binomial Regression
STATISTICS COLUMN Negative Binomial Regression Shengping Yang PhD ,Gilbert Berdine MD In the hospital stay study discussed recently, it was mentioned that “in case overdispersion exists, Poisson regression model might not be appropriate.” I would like to know more about the appropriate modeling method in that case. Although Poisson regression modeling is wide- regression is commonly recommended. ly used in count data analysis, it does have a limita- tion, i.e., it assumes that the conditional distribution The Poisson distribution can be considered to of the outcome variable is Poisson, which requires be a special case of the negative binomial distribution. that the mean and variance be equal. The data are The negative binomial considers the results of a se- said to be overdispersed when the variance exceeds ries of trials that can be considered either a success the mean. Overdispersion is expected for contagious or failure. A parameter ψ is introduced to indicate the events where the first occurrence makes a second number of failures that stops the count. The negative occurrence more likely, though still random. Poisson binomial distribution is the discrete probability func- regression of overdispersed data leads to a deflated tion that there will be a given number of successes standard error and inflated test statistics. Overdisper- before ψ failures. The negative binomial distribution sion may also result when the success outcome is will converge to a Poisson distribution for large ψ. not rare. To handle such a situation, negative binomial 0 5 10 15 20 25 0 5 10 15 20 25 Figure 1. Comparison of Poisson and negative binomial distributions. -

Generalized Linear Models
CHAPTER 6 Generalized linear models 6.1 Introduction Generalized linear modeling is a framework for statistical analysis that includes linear and logistic regression as special cases. Linear regression directly predicts continuous data y from a linear predictor Xβ = β0 + X1β1 + + Xkβk.Logistic regression predicts Pr(y =1)forbinarydatafromalinearpredictorwithaninverse-··· logit transformation. A generalized linear model involves: 1. A data vector y =(y1,...,yn) 2. Predictors X and coefficients β,formingalinearpredictorXβ 1 3. A link function g,yieldingavectoroftransformeddataˆy = g− (Xβ)thatare used to model the data 4. A data distribution, p(y yˆ) | 5. Possibly other parameters, such as variances, overdispersions, and cutpoints, involved in the predictors, link function, and data distribution. The options in a generalized linear model are the transformation g and the data distribution p. In linear regression,thetransformationistheidentity(thatis,g(u) u)and • the data distribution is normal, with standard deviation σ estimated from≡ data. 1 1 In logistic regression,thetransformationistheinverse-logit,g− (u)=logit− (u) • (see Figure 5.2a on page 80) and the data distribution is defined by the proba- bility for binary data: Pr(y =1)=y ˆ. This chapter discusses several other classes of generalized linear model, which we list here for convenience: The Poisson model (Section 6.2) is used for count data; that is, where each • data point yi can equal 0, 1, 2, ....Theusualtransformationg used here is the logarithmic, so that g(u)=exp(u)transformsacontinuouslinearpredictorXiβ to a positivey ˆi.ThedatadistributionisPoisson. It is usually a good idea to add a parameter to this model to capture overdis- persion,thatis,variationinthedatabeyondwhatwouldbepredictedfromthe Poisson distribution alone. -

Modeling Overdispersion with the Normalized Tempered Stable Distribution
Modeling overdispersion with the normalized tempered stable distribution M. Kolossiatisa, J.E. Griffinb, M. F. J. Steel∗,c aDepartment of Hotel and Tourism Management, Cyprus University of Technology, P.O. Box 50329, 3603 Limassol, Cyprus. bInstitute of Mathematics, Statistics and Actuarial Science, University of Kent, Canterbury, CT2 7NF, U.K. cDepartment of Statistics, University of Warwick, Coventry, CV4 7AL, U.K. Abstract A multivariate distribution which generalizes the Dirichlet distribution is intro- duced and its use for modeling overdispersion in count data is discussed. The distribution is constructed by normalizing a vector of independent tempered sta- ble random variables. General formulae for all moments and cross-moments of the distribution are derived and they are found to have similar forms to those for the Dirichlet distribution. The univariate version of the distribution can be used as a mixing distribution for the success probability of a binomial distribution to define an alternative to the well-studied beta-binomial distribution. Examples of fitting this model to simulated and real data are presented. Keywords: Distribution on the unit simplex; Mice fetal mortality; Mixed bino- mial; Normalized random measure; Overdispersion 1. Introduction In many experiments we observe data as the number of observations in a sam- ple with some property. The binomial distribution is a natural model for this type of data. However, the data are often found to be overdispersed relative to that ∗Corresponding author. Tel.: +44-2476-523369; fax: +44-2476-524532 Email addresses: [email protected] (M. Kolossiatis), [email protected] (J.E. Griffin), [email protected] (M. -

Variance Partitioning in Multilevel Logistic Models That Exhibit Overdispersion
J. R. Statist. Soc. A (2005) 168, Part 3, pp. 599–613 Variance partitioning in multilevel logistic models that exhibit overdispersion W. J. Browne, University of Nottingham, UK S. V. Subramanian, Harvard School of Public Health, Boston, USA K. Jones University of Bristol, UK and H. Goldstein Institute of Education, London, UK [Received July 2002. Final revision September 2004] Summary. A common application of multilevel models is to apportion the variance in the response according to the different levels of the data.Whereas partitioning variances is straight- forward in models with a continuous response variable with a normal error distribution at each level, the extension of this partitioning to models with binary responses or to proportions or counts is less obvious. We describe methodology due to Goldstein and co-workers for appor- tioning variance that is attributable to higher levels in multilevel binomial logistic models. This partitioning they referred to as the variance partition coefficient. We consider extending the vari- ance partition coefficient concept to data sets when the response is a proportion and where the binomial assumption may not be appropriate owing to overdispersion in the response variable. Using the literacy data from the 1991 Indian census we estimate simple and complex variance partition coefficients at multiple levels of geography in models with significant overdispersion and thereby establish the relative importance of different geographic levels that influence edu- cational disparities in India. Keywords: Contextual variation; Illiteracy; India; Multilevel modelling; Multiple spatial levels; Overdispersion; Variance partition coefficient 1. Introduction Multilevel regression models (Goldstein, 2003; Bryk and Raudenbush, 1992) are increasingly being applied in many areas of quantitative research. -
Meta-Analysis of Count Data What Is Count Data Complicated by What Is
What is count data Meta-analysis of count data • Data that can only take the non-negative integer values 0, 1, 2, 3, ……. • Examples in RCTs – Episodes of exacerbation of asthma – Falls Peter Herbison – Number of incontinence episodes Department of Preventive and • Time scale can vary from the whole study Social Medicine period to the last few (pick your time University of Otago period). Complicated by What is large? • Different exposure times .4 – Withdrawals .3 – Deaths – Different diary periods .2 • Sometimes people only fill out some days of the Probability diary as well as the periods being different .1 • Counts with a large mean can be treated 0 as normally distributed 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 n Mean 1 Mean 2 Mean 3 Mean 4 Mean 5 Analysis as rates Meta-analysis of rate ratios • Count number of events in each arm • Formula for calculation in Handbook • Calculate person years at risk in each arm • Straightforward using generic inverse • Calculate rates in each arm variance • Divide to get a rate ratio • In addition to the one reference in the • Can also be done by poisson regression Handbook: family – Guevara et al. Meta-analytic methods for – Poisson, negative binomial, zero inflated pooling rates when follow up duration varies: poisson a case study. BMC Medical Research – Assumes constant underlying risk Methodology 2004;4:17 Dichotimizing Treat as continuous • Change data so that it is those who have • May not be too bad one or more events versus those who • Handbook says beware of skewness have none • Get a 2x2 table • Good if the purpose of the treatment is to prevent events rather than reduce the number of them • Meta-analyse as usual Time to event Not so helpful • Usually time to first event but repeated • Many people look at the distribution and events can be used think that the only distribution that exists is • Analyse by survival analysis (e.g. -

Generalized Linear Models and Point Count Data: Statistical Considerations for the Design and Analysis of Monitoring Studies
Generalized Linear Models and Point Count Data: Statistical Considerations for the Design and Analysis of Monitoring Studies Nathaniel E. Seavy,1,2,3 Suhel Quader,1,4 John D. Alexander,2 and C. John Ralph5 ________________________________________ Abstract The success of avian monitoring programs to effec- Key words: Generalized linear models, juniper remov- tively guide management decisions requires that stud- al, monitoring, overdispersion, point count, Poisson. ies be efficiently designed and data be properly ana- lyzed. A complicating factor is that point count surveys often generate data with non-normal distributional pro- perties. In this paper we review methods of dealing with deviations from normal assumptions, and we Introduction focus on the application of generalized linear models (GLMs). We also discuss problems associated with Measuring changes in bird abundance over time and in overdispersion (more variation than expected). In order response to habitat management is widely recognized to evaluate the statistical power of these models to as an important aspect of ecological monitoring detect differences in bird abundance, it is necessary for (Greenwood et al. 1993). The use of long-term avian biologists to identify the effect size they believe is monitoring programs (e.g., the Breeding Bird Survey) biologically significant in their system. We illustrate to identify population trends is a powerful tool for bird one solution to this challenge by discussing the design conservation (Sauer and Droege 1990, Sauer and Link of a monitoring program intended to detect changes in 2002). Short-term studies comparing bird abundance in bird abundance as a result of Western juniper (Juniper- treated and untreated areas are also important because us occidentalis) reduction projects in central Oregon. -

Handling Overdispersion with Negative Binomial and Generalized Poisson Regression Models
Handling Overdispersion with Negative Binomial and Generalized Poisson Regression Models Noriszura Ismail and Abdul Aziz Jemain Abstract In actuarial hteramre, researchers suggested various statistical procedures to estimate the parameters in claim count or frequency model. In particular, the Poisson regression model, which is also known as the Generahzed Linear Model (GLM) with Poisson error structure, has been x~adely used in the recent years. However, it is also recognized that the count or frequency data m insurance practice often display overdispersion, i.e., a situation where the variance of the response variable exceeds the mean. Inappropriate imposition of the Poisson may underestimate the standard errors and overstate the sigruficance of the regression parameters, and consequently, giving misleading inference about the regression parameters. This paper suggests the Negative Binomial and Generalized Poisson regression models as ahemafives for handling overdispersion. If the Negative Binomial and Generahzed Poisson regression models are fitted by the maximum likelihood method, the models are considered to be convenient and practical; they handle overdispersion, they allow the likelihood ratio and other standard maximum likelihood tests to be implemented, they have good properties, and they permit the fitting procedure to be carried out by using the herative Weighted I_,east Squares OWLS) regression similar to those of the Poisson. In this paper, two types of regression model will be discussed and applied; multiplicative and additive. The multiplicative and additive regression models for Poisson, Negative Binomial and Generalized Poisson will be fitted, tested and compared on three different sets of claim frequency data; Malaysian private motor third partT property' damage data, ship damage incident data from McCuUagh and Nelder, and data from Bailey and Simon on Canadian private automobile liabili~,. -

Stat 5421 Lecture Notes: Overdispersion
Stat 5421 Lecture Notes: Overdispersion Charles J. Geyer November 20, 2020 Contents 1 License 1 2 R 1 3 Quasilikelihood and Estimating Equations1 3.1 Variance Functions..........................................1 3.2 Modeling without Models......................................2 3.3 Estimating the Dispersion Parameter................................3 4 Example: Agresti Section 4.7.43 4.1 Testing for Overdispersion......................................7 4.2 On Not Testing for Overdispersion.................................8 5 Example: Agresti Section 4.7.28 1 License This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License (http: //creativecommons.org/licenses/by-sa/4.0/). 2 R • The version of R used to make this document is 4.0.3. • The version of the rmarkdown package used to make this document is 2.5. 3 Quasilikelihood and Estimating Equations 3.1 Variance Functions In linear models (fit by R function lm) we assume the components of the response vector are independent, normally distributed, and same variance (homoscedastic). The variance is unrelated to the mean. The mean of each component can be any real number. The common variance of all the components can be any positive real number. In generalized linear models (fit by R function glm) none of these assumptions hold except the components of the response vector are independent. 1 • There are constraints on the means. • There is only one parameter for binomial and Poisson models, so the variance and mean cannot be separately varied. For binomial regression, • components of the response vector are independent Binomial(ni, πi) distributed. • Means µi = niπi satisfy 0 ≤ µi ≤ ni. • Variances are a function of means var(yi) = niV (πi) = niπi(1 − πi) where V (π) = π(1 − π) For Poisson regression, • components of the response vector are independent Poisson(µi) distributed. -

Count Data Models
Count Data Models CIVL 7012/8012 2 In Today’s Class • Count data models • Poisson Models • Overdispersion • Negative binomial distribution models • Comparison • Zero-inflated models • R-implementation 3 Count Data In many a phenomena the regressand is of the count type, such as: The number of patents received by a firm in a year The number of visits to a dentist in a year The number of speeding tickets received in a year The underlying variable is discrete, taking only a finite non- negative number of values. In many cases the count is 0 for several observations Each count example is measured over a certain finite time period. 4 Models for Count Data Poisson Probability Distribution: Regression models based on this probability distribution are known as Poisson Regression Models (PRM). Negative Binomial Probability Distribution: An alternative to PRM is the Negative Binomial Regression Model (NBRM), used to remedy some of the deficiencies of the PRM. 5 Can we apply OLS Patent data from 181firms LR 90: log (R&D Expenditure) Dummy categories • AEROSP: Aerospace • CHEMIST: Chemistry • Computer: Comp Sc. • Machines: Instrumental Engg • Vehicles: Auto Engg. • Reference: Food, fuel others Dummy countries • Japan: • US: • Reference: European countries 6 Inferences from the example (1) • R&D have +ve influence – 1% increase in R&D expenditure increases the likelihood of patent increase by 0.73% ceteris paribus • Chemistry has received 47 more patents compared to the reference category • Similarly vehicles industry has received 191 lower patents