DOCSLIB.ORG

Bayesian Generalized Linear Model for Over and Under Dispersed Counts

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Bayesian Generalized Linear Model for Over and Under Dispersed Counts Bayesian generalized linear model for over and under dispersed counts Alan Huang1, and Andy Sang Il Kim2 1University of Queensland, Nanyang Technological University, and 2University of Technology Sydney Abstract. Bayesian models that can handle both over and under dis- persed counts are rare in the literature, perhaps because full probabil- ity distributions for dispersed counts are rather difficult to construct. This note takes a first look at Bayesian Conway-Maxwell-Poisson gen- eralized linear models that can handle both over and under dispersion yet retain the parsimony and interpretability of classical count regres- sion models. The focus is on providing an explicit demonstration of Bayesian regression inferences for dispersed counts via a Metropolis- Hastings algorithm. We illustrate the approach on two data analysis examples and demonstrate some favourable frequentist properties via a simulation study. Key words and phrases: Bayesian generalized linear model, Count data, Overdispersion, Underdispersion, Conway-Maxwell-Poisson. 1. INTRODUCTION Count data often exhibit dispersion relative to a classical Poisson model. For overdispersed counts, where the conditional variance is larger than the conditional mean, models based on the negative binomial, Poisson inverse-Gaussian and other Poisson rate mixture distributions have been well-covered in the literature from both frequentist and Bayesian points of view (e.g., Wilmot, 1987; McCullagh and Nelder, 1989; Gelman & Hill, 2007). For underdispersed counts, where the conditional variance is smaller than the conditional mean, the options are far more limited due to the difficulty in constructing full probability distributions that can handle underdispersion. A recent survey of a handful of existing models can be found in Sellers & Morris(2017). The lack of options is particularly detrimental from a Bayesian point of view because a full probability distribution for the data is required for the application of Bayes' theorem to determine the posterior distribution and subsequent inferences. arXiv:1910.06008v2 [stat.ME] 25 Oct 2019 This note takes a first step towards filling this gap in the literature by presenting a Bayesian framework for the regression modelling of counts that can (i) handle both over and under dispersion, and (ii) retain the same level of parsimony and interpretability as classical counts models. We do this by building on a recent reparametrisation of the Conway-Maxwell-Poisson distribution (CMP) that allows the mean to be modelled directly (Huang, 2017), so that simple and interpretable models, such as a log-linear model, can be constructed for both over and under dispersed counts. This places underdispersed counts on the same footing as School of Mathematics and Physics, University of Queensland, St Lucia, QLD, Australia 4072 (e-mail: [email protected]). School of Mathematical and Physical Sciences, University of Technology Sydney, Ultimo, NSW, Australia 2007 (e-mail: [email protected]). 1 2 A. HUANG & A. S. I. KIM equidispersed and overdispersed counts which are readily handled by the familiar Poisson and negative binomial models, respectively. More specifically, the mean-parametrized CMP distribution with mean µ > 0 and dispersion ν ≥ 0 is characterized by the probability mass function λ(µ, ν)y 1 (1.1) P (Y = yjµ, ν) = ; y = 0; 1; 2;:::; (y!)ν Z(λ(µ, ν); ν) where the rate λ(µ, ν) is a function of µ and ν given by the solution to 1 X λy 0 = (y − µ) ; (y!)ν y=0 P1 y ν and Z(λ, ν) = y=0 λ =(y!) is a normalizing function. It is easy to show that ν < 1 implies overdispersion and ν > 1 implies underdispersion relative to a Poisson distribution of the same mean. When ν = 1, the distribution coincides with the Poisson distribution. We write CMPµ(µ, ν) for the mean-parametrized CMP distribution (1.1) to distinguish it from the standard CMP distribution of Shmueli et. al. (2005). CMPµ distributions are particularly useful for modelling dispersed counts because they re- tain all the attractive properties of standard CMP distributions whilst being able to model the mean directly (Huang, 2017; Andrianatos, 2017). They form two-parameter exponential families, and for fixed or given values of the dispersion they become one-parameter exponen- tial families, making them immediately adaptable to regression modelling via the generalized linear model (GLM, McCullagh and Nelder, 1989) framework. They also form a continuous bridge between other classical models, passing through the geometric and Poisson distribu- tions as special cases, with the Bernoulli distribution as a limiting case. Moreover, unlike the generalized Poisson (Consul & Famoye, 1992), quasi-Poisson (Wedderburn, 1974), and the recently-proposed Extended Poisson-Tweedie (Bonat et. al., 2018) models, CMPµ distributions always correspond to full probability models for any choice of model parameters, covering both over and under dispersion. This makes them particularly suitable for Bayesian modelling and inferences. From a Bayesian point of view, Kadane et. al. (2006) explored the use of conjugate priors for the standard CMP distribution in the independent and identically distributed case. While this can be easily extended to mean-parametrized CMP distributions (see Online Supplement), there are three practical limitations of using the conjugate prior. First, the subsequent posterior is known only up to a normalizing constant that has no closed-form, so computing it requires either numerical integration, Markov Chain Monte Carlo (MCMC) sampling, or some other approximation method. There is therefore no practical advantage of using the conjugate prior over any other prior. Second, appropriate specification of the hyperparameters can be rather opaque due to the unfamiliar form of the conjugate prior. Kadane et. al. (2006) offer an applet to translate prior information into an appropriate elucidation of hyperparameters, but a simpler and more interpretable prior can mitigate this issue altogether. Finally, the conjugacy property only holds for intercept-only models, and the extension to the regression case in which the mean of each observation may depend on a set of covariates is not at all immediate. This is in fact true of most Bayesian generalized linear models { for example, while the Gamma distribution is conjugate for the Poisson distribution for intercept-only models, there is no extension to the Poisson regression case (Hoff, 2009, page 173). Instead, multivariate normal priors are placed on the regression coefficients for interpretability and parsimony (as implemented in the popular MCMCpack package in R by Martin et. al. (2011), for example). BAYESIAN GLM FOR DISPERSED COUNTS 3 To the best of our knowledge, this note is the first to consider a Bayesian framework for the regression modelling of both over and under dispersed counts that circumvents these lim- itations, yet retains the parsimony and interpretability of familiar count models such as the log-linear Poisson and negative binomial models. This work is part of a larger ongoing project that looks at efficient Bayesian inferences for dispersed counts in hierarchical models. 2. BAYESIAN CMP GENERALIZED LINEAR MODEL FOR DISPERSED COUNTS Suppose we have independent observation pairs (y1; X1); (y2; X2) ::: , where each yi is a p count response and each Xi 2 R is a corresponding set of covariates. A CMPµ generalized linear model for the data that can handle both over and under dispersion can be specified via ind: > (2.1) yijXi ∼ CMPµ µ(Xi β); ν ; i = 1; 2;:::; p where β 2 R is a vector of regression coefficients, ν ≥ 0 is a dispersion parameter, and (in a slight abuse of notation) µ(·) is a user-specified mean-model or inverse-link function. For this note, we focus on the popular log-linear model, E(yjX) = µ(X>β) = exp(X>β); so that each component of β can be interpreted as the expected change in the mean response (on the log scale) for a unit increase in the corresponding component of X. Of course, other link functions can be considered, as with any GLM. Indeed, the key advantage of the CMPµ distribution is that is directly parametrized via the mean so that simple, easily-interpretable mean-models can be considered. In contrast, standard CMP distributions (Shmueli et. al., 2005; Lord et. al., 2008; Sellers & Shmueli, 2010) and its variants (e.g., Guikema & Coffelt, 2008) model either a latent rate parameter or some power transformation of it, which cannot be interpreted as the mean. For a Bayesian model specification, we need a prior distribution on the model parameters β and ν. In this note, we focus on easily interpretable prior specifications, such as 2 (2.2) β ∼ N(µβ; Σβ) and ν ∼ Log-Normal(µν; σν) ; 2 so that the hyperparameters (µβ; Σβ) and (µν; σν) have clear interpretations as prior means and variances. This makes it easy to translate prior beliefs about the data-generating process into sensible specification of hyperparameter values. In contrast, the conjugate prior of Kadane et. al. (2006) has no clear interpretation, making elucidation of hyperparameter values rather opaque. Of course, the prior distribution in (2.2) can be replaced with any user-specified prior, with the proposed method in this note being applicable for any prior specification. Note that taking the prior variances in (2.2) to be arbitrarily large leads to improper flat priors, p(β); p(ν) / 1, which we consider in Section 4.3 and in the Online Supplement. When the normal and log-normal priors (2.2) are used, the joint posterior of the parameters β and ν given the observed data y ≡ (y1; : : : ; yn) has the form, n y −1 Y > i > −ν (2.3) p(β; νjy; X) / λ exp(Xi β); ν Z λ(exp(Xi β); ν); ν yi i=1 1 × exp − (β − µ )>Σ−1(β − µ ) 2 β β β 2 −1 (log ν − µν) ×ν exp − 2 ; 2σν 4 A. HUANG & A. S. I. KIM which is known up to a normalizing constant.
Load more

Recommended publications
  • An Introduction to Poisson Regression Russ Lavery, K&L Consulting Services, King of Prussia, PA, U.S.A
    NESUG 2010 Statistics and Analysis An Animated Guide: An Introduction To Poisson Regression Russ Lavery, K&L Consulting Services, King of Prussia, PA, U.S.A. ABSTRACT: This paper will be a brief introduction to Poisson regression (theory, steps to be followed, complications and interpretation) via a worked example. It is hoped that this will increase motivation towards learning this useful statistical technique. INTRODUCTION: Poisson regression is available in SAS through the GENMOD procedure (generalized modeling). It is appropriate when: 1) the process that generates the conditional Y distributions would, theoretically, be expected to be a Poisson random process and 2) when there is no evidence of overdispersion and 3) when the mean of the marginal distribution is less than ten (preferably less than five and ideally close to one). THE POISSON DISTRIBUTION: The Poison distribution is a discrete Percent of observations where the random variable X is expected distribution and is appropriate for to have the value x, given that the Poisson distribution has a mean modeling counts of observations. of λ= P(X=x, λ ) = (e - λ * λ X) / X! Counts are observed cases, like the 0.4 count of measles cases in cities. You λ can simply model counts if all data 0.35 were collected in the same measuring 0.3 unit (e.g. the same number of days or 0.3 0.5 0.8 same number of square feet). 0.25 λ 1 0.2 3 You can use the Poisson Distribution = 5 for modeling rates (rates are counts 0.15 20 per unit) if the units of collection were 8 different.
    [Show full text]
  • Generalized Linear Models (Glms)
    San Jos´eState University Math 261A: Regression Theory & Methods Generalized Linear Models (GLMs) Dr. Guangliang Chen This lecture is based on the following textbook sections: • Chapter 13: 13.1 – 13.3 Outline of this presentation: • What is a GLM? • Logistic regression • Poisson regression Generalized Linear Models (GLMs) What is a GLM? In ordinary linear regression, we assume that the response is a linear function of the regressors plus Gaussian noise: 0 2 y = β0 + β1x1 + ··· + βkxk + ∼ N(x β, σ ) | {z } |{z} linear form x0β N(0,σ2) noise The model can be reformulate in terms of • distribution of the response: y | x ∼ N(µ, σ2), and • dependence of the mean on the predictors: µ = E(y | x) = x0β Dr. Guangliang Chen | Mathematics & Statistics, San Jos´e State University3/24 Generalized Linear Models (GLMs) beta=(1,2) 5 4 3 β0 + β1x b y 2 y 1 0 −1 0.0 0.2 0.4 0.6 0.8 1.0 x x Dr. Guangliang Chen | Mathematics & Statistics, San Jos´e State University4/24 Generalized Linear Models (GLMs) Generalized linear models (GLM) extend linear regression by allowing the response variable to have • a general distribution (with mean µ = E(y | x)) and • a mean that depends on the predictors through a link function g: That is, g(µ) = β0x or equivalently, µ = g−1(β0x) Dr. Guangliang Chen | Mathematics & Statistics, San Jos´e State University5/24 Generalized Linear Models (GLMs) In GLM, the response is typically assumed to have a distribution in the exponential family, which is a large class of probability distributions that have pdfs of the form f(x | θ) = a(x)b(θ) exp(c(θ) · T (x)), including • Normal - ordinary linear regression • Bernoulli - Logistic regression, modeling binary data • Binomial - Multinomial logistic regression, modeling general cate- gorical data • Poisson - Poisson regression, modeling count data • Exponential, Gamma - survival analysis Dr.
    [Show full text]
  • Generalized Linear Models with Poisson Family: Applications in Ecology
    UNIVERSITY OF ABOMEY- CALAVI *********** FACULTY OF AGRONOMIC SCIENCES *************** **************** Master Program in Statistics, Major Biostatistics 1st batch Generalized linear models with Poisson family: applications in ecology A thesis submitted to the Faculty of Agronomic Sciences in partial fulfillment of the requirements for the degree of the Master of Sciences in Biostatistics Presented by: LOKONON Enagnon Bruno Supervisor: Pr Romain L. GLELE KAKAÏ, Professor of Biostatistics and Forest estimation Academic year: 2014-2015 UNIVERSITE D’ABOMEY- CALAVI *********** FACULTE DES SCIENCES AGRONOMIQUES *************** ************** Programme de Master en Biostatistiques 1ère Promotion Modèles linéaires généralisés de la famille de Poisson : applications en écologie Mémoire soumis à la Faculté des Sciences Agronomiques pour obtenir le Diplôme de Master recherche en Biostatistiques Présenté par: LOKONON Enagnon Bruno Superviseur: Pr Romain L. GLELE KAKAÏ, Professeur titulaire de Biostatistiques et estimation forestière Année académique: 2014-2015 Certification I certify that this work has been achieved by LOKONON E. Bruno under my entire supervision at the University of Abomey-Calavi (Benin) in order to obtain his Master of Science degree in Biostatistics. Pr Romain L. GLELE KAKAÏ Professor of Biostatistics and Forest estimation i Acknowledgements This research was supported by WAAPP/PPAAO-BENIN (West African Agricultural Productivity Program/ Programme de Productivité Agricole en Afrique de l‟Ouest). This dissertation could only have been possible through the generous contributions of many people. First and foremost, I am grateful to my supervisor Pr Romain L. GLELE KAKAÏ, Professor of Biostatistics and Forest estimation who tirelessly played key role in orientation, scientific writing and mentoring during this research. In particular, I thank him for his prompt availability whenever needed.
    [Show full text]
  • Overdispersion, and How to Deal with It in R and JAGS (Requires R-Packages AER, Coda, Lme4, R2jags, Dharma/Devtools) Carsten F
    Overdispersion, and how to deal with it in R and JAGS (requires R-packages AER, coda, lme4, R2jags, DHARMa/devtools) Carsten F. Dormann 07 December, 2016 Contents 1 Introduction: what is overdispersion? 1 2 Recognising (and testing for) overdispersion 1 3 “Fixing” overdispersion 5 3.1 Quasi-families . .5 3.2 Different distribution (here: negative binomial) . .6 3.3 Observation-level random effects (OLRE) . .8 4 Overdispersion in JAGS 12 1 Introduction: what is overdispersion? Overdispersion describes the observation that variation is higher than would be expected. Some distributions do not have a parameter to fit variability of the observation. For example, the normal distribution does that through the parameter σ (i.e. the standard deviation of the model), which is constant in a typical regression. In contrast, the Poisson distribution has no such parameter, and in fact the variance increases with the mean (i.e. the variance and the mean have the same value). In this latter case, for an expected value of E(y) = 5, we also expect that the variance of observed data points is 5. But what if it is not? What if the observed variance is much higher, i.e. if the data are overdispersed? (Note that it could also be lower, underdispersed. This is less often the case, and not all approaches below allow for modelling underdispersion, but some do.) Overdispersion arises in different ways, most commonly through “clumping”. Imagine the number of seedlings in a forest plot. Depending on the distance to the source tree, there may be many (hundreds) or none. The same goes for shooting stars: either the sky is empty, or littered with shooting stars.
    [Show full text]
  • Poisson Versus Negative Binomial Regression
    Handling Count Data The Negative Binomial Distribution Other Applications and Analysis in R References Poisson versus Negative Binomial Regression Randall Reese Utah State University [email protected] February 29, 2016 Randall Reese Poisson and Neg. Binom Handling Count Data The Negative Binomial Distribution Other Applications and Analysis in R References Overview 1 Handling Count Data ADEM Overdispersion 2 The Negative Binomial Distribution Foundations of Negative Binomial Distribution Basic Properties of the Negative Binomial Distribution Fitting the Negative Binomial Model 3 Other Applications and Analysis in R 4 References Randall Reese Poisson and Neg. Binom Handling Count Data The Negative Binomial Distribution ADEM Other Applications and Analysis in R Overdispersion References Count Data Randall Reese Poisson and Neg. Binom Handling Count Data The Negative Binomial Distribution ADEM Other Applications and Analysis in R Overdispersion References Count Data Data whose values come from Z≥0, the non-negative integers. Classic example is deaths in the Prussian army per year by horse kick (Bortkiewicz) Example 2 of Notes 5. (Number of successful \attempts"). Randall Reese Poisson and Neg. Binom Handling Count Data The Negative Binomial Distribution ADEM Other Applications and Analysis in R Overdispersion References Poisson Distribution Support is the non-negative integers. (Count data). Described by a single parameter λ > 0. When Y ∼ Poisson(λ), then E(Y ) = Var(Y ) = λ Randall Reese Poisson and Neg. Binom Handling Count Data The Negative Binomial Distribution ADEM Other Applications and Analysis in R Overdispersion References Acute Disseminated Encephalomyelitis Acute Disseminated Encephalomyelitis (ADEM) is a neurological, immune disorder in which widespread inflammation of the brain and spinal cord damages tissue known as white matter.
    [Show full text]
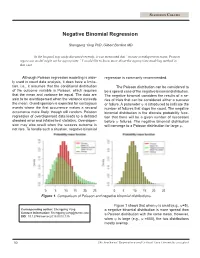
  • Negative Binomial Regression
    STATISTICS COLUMN Negative Binomial Regression Shengping Yang PhD ,Gilbert Berdine MD In the hospital stay study discussed recently, it was mentioned that “in case overdispersion exists, Poisson regression model might not be appropriate.” I would like to know more about the appropriate modeling method in that case. Although Poisson regression modeling is wide- regression is commonly recommended. ly used in count data analysis, it does have a limita- tion, i.e., it assumes that the conditional distribution The Poisson distribution can be considered to of the outcome variable is Poisson, which requires be a special case of the negative binomial distribution. that the mean and variance be equal. The data are The negative binomial considers the results of a se- said to be overdispersed when the variance exceeds ries of trials that can be considered either a success the mean. Overdispersion is expected for contagious or failure. A parameter ψ is introduced to indicate the events where the first occurrence makes a second number of failures that stops the count. The negative occurrence more likely, though still random. Poisson binomial distribution is the discrete probability func- regression of overdispersed data leads to a deflated tion that there will be a given number of successes standard error and inflated test statistics. Overdisper- before ψ failures. The negative binomial distribution sion may also result when the success outcome is will converge to a Poisson distribution for large ψ. not rare. To handle such a situation, negative binomial 0 5 10 15 20 25 0 5 10 15 20 25 Figure 1. Comparison of Poisson and negative binomial distributions.
    [Show full text]
  • Heteroscedastic Errors
    Heteroscedastic Errors ◮ Sometimes plots and/or tests show that the error variances 2 σi = Var(ǫi ) depend on i ◮ Several standard approaches to fixing the problem, depending on the nature of the dependence. ◮ Weighted Least Squares. ◮ Transformation of the response. ◮ Generalized Linear Models. Richard Lockhart STAT 350: Heteroscedastic Errors and GLIM Weighted Least Squares ◮ Suppose variances are known except for a constant factor. 2 2 ◮ That is, σi = σ /wi . ◮ Use weighted least squares. (See Chapter 10 in the text.) ◮ This usually arises realistically in the following situations: ◮ Yi is an average of ni measurements where you know ni . Then wi = ni . 2 ◮ Plots suggest that σi might be proportional to some power of 2 γ γ some covariate: σi = kxi . Then wi = xi− . Richard Lockhart STAT 350: Heteroscedastic Errors and GLIM Variances depending on (mean of) Y ◮ Two standard approaches are available: ◮ Older approach is transformation. ◮ Newer approach is use of generalized linear model; see STAT 402. Richard Lockhart STAT 350: Heteroscedastic Errors and GLIM Transformation ◮ Compute Yi∗ = g(Yi ) for some function g like logarithm or square root. ◮ Then regress Yi∗ on the covariates. ◮ This approach sometimes works for skewed response variables like income; ◮ after transformation we occasionally find the errors are more nearly normal, more homoscedastic and that the model is simpler. ◮ See page 130ff and check under transformations and Box-Cox in the index. Richard Lockhart STAT 350: Heteroscedastic Errors and GLIM Generalized Linear Models ◮ Transformation uses the model T E(g(Yi )) = xi β while generalized linear models use T g(E(Yi )) = xi β ◮ Generally latter approach offers more flexibility.
    [Show full text]
  • Generalized Linear Models
    CHAPTER 6 Generalized linear models 6.1 Introduction Generalized linear modeling is a framework for statistical analysis that includes linear and logistic regression as special cases. Linear regression directly predicts continuous data y from a linear predictor Xβ = β0 + X1β1 + + Xkβk.Logistic regression predicts Pr(y =1)forbinarydatafromalinearpredictorwithaninverse-··· logit transformation. A generalized linear model involves: 1. A data vector y =(y1,...,yn) 2. Predictors X and coefficients β,formingalinearpredictorXβ 1 3. A link function g,yieldingavectoroftransformeddataˆy = g− (Xβ)thatare used to model the data 4. A data distribution, p(y yˆ) | 5. Possibly other parameters, such as variances, overdispersions, and cutpoints, involved in the predictors, link function, and data distribution. The options in a generalized linear model are the transformation g and the data distribution p. In linear regression,thetransformationistheidentity(thatis,g(u) u)and • the data distribution is normal, with standard deviation σ estimated from≡ data. 1 1 In logistic regression,thetransformationistheinverse-logit,g− (u)=logit− (u) • (see Figure 5.2a on page 80) and the data distribution is defined by the proba- bility for binary data: Pr(y =1)=y ˆ. This chapter discusses several other classes of generalized linear model, which we list here for convenience: The Poisson model (Section 6.2) is used for count data; that is, where each • data point yi can equal 0, 1, 2, ....Theusualtransformationg used here is the logarithmic, so that g(u)=exp(u)transformsacontinuouslinearpredictorXiβ to a positivey ˆi.ThedatadistributionisPoisson. It is usually a good idea to add a parameter to this model to capture overdis- persion,thatis,variationinthedatabeyondwhatwouldbepredictedfromthe Poisson distribution alone.
    [Show full text]
  • Modeling Overdispersion with the Normalized Tempered Stable Distribution
    Modeling overdispersion with the normalized tempered stable distribution M. Kolossiatisa, J.E. Griffinb, M. F. J. Steel∗,c aDepartment of Hotel and Tourism Management, Cyprus University of Technology, P.O. Box 50329, 3603 Limassol, Cyprus. bInstitute of Mathematics, Statistics and Actuarial Science, University of Kent, Canterbury, CT2 7NF, U.K. cDepartment of Statistics, University of Warwick, Coventry, CV4 7AL, U.K. Abstract A multivariate distribution which generalizes the Dirichlet distribution is intro- duced and its use for modeling overdispersion in count data is discussed. The distribution is constructed by normalizing a vector of independent tempered sta- ble random variables. General formulae for all moments and cross-moments of the distribution are derived and they are found to have similar forms to those for the Dirichlet distribution. The univariate version of the distribution can be used as a mixing distribution for the success probability of a binomial distribution to define an alternative to the well-studied beta-binomial distribution. Examples of fitting this model to simulated and real data are presented. Keywords: Distribution on the unit simplex; Mice fetal mortality; Mixed bino- mial; Normalized random measure; Overdispersion 1. Introduction In many experiments we observe data as the number of observations in a sam- ple with some property. The binomial distribution is a natural model for this type of data. However, the data are often found to be overdispersed relative to that ∗Corresponding author. Tel.: +44-2476-523369; fax: +44-2476-524532 Email addresses: [email protected] (M. Kolossiatis), [email protected] (J.E. Griffin), [email protected] (M.
    [Show full text]
  • Bayesian Hierarchical Poisson Regression Model for Overdispersed Count Data
    Bayesian Hierarchical Poisson Regression Model for Overdispersed Count Data Overview This example uses the RANDOM statement in MCMC procedure to fit a Bayesian hierarchical Poisson regression model to overdispersed count data. The RANDOM statement, available in SAS/STAT 9.3 and later, provides a convenient way to specify random effects with substantionally improved performance. Overdispersion occurs when count data appear more dispersed than expected under a reference model. Overdispersion can be caused by positive correlation among the observations, an incorrect model, an in- correct distributional specification, or incorrect variance functions. The example displays how Bayesian hierarchical Poisson regression models are effective in capturing overdispersion and providing a better fit. The SAS source code for this example is available as a text file attachment. In Adobe Acrobat, right-click the icon in the margin and select Save Embedded File to Disk. You can also double-click the icon to open the file immediately. Analysis Count data frequently display overdispersion (more variation than expected from a standard parametric model). Breslow(1984) discusses these types of models and suggests several different ways to model them. Hierarchical Poisson models have been found effective in capturing the overdispersion in data sets with extra Poisson variation. Hierarchical Poisson regression models are expressed as Poisson models with a log link and a normal vari- ance on the mean parameter. More formally, a hierarchical Poisson regression model is written as Yij ij Poisson.ij / j log.ij / Xi ˇ ij D C 2 ij normal.0; / for i 1; :::; n, j 1; :::; J , and y 0; 1; 2; ::: .
    [Show full text]
  • Variance Partitioning in Multilevel Logistic Models That Exhibit Overdispersion
    J. R. Statist. Soc. A (2005) 168, Part 3, pp. 599–613 Variance partitioning in multilevel logistic models that exhibit overdispersion W. J. Browne, University of Nottingham, UK S. V. Subramanian, Harvard School of Public Health, Boston, USA K. Jones University of Bristol, UK and H. Goldstein Institute of Education, London, UK [Received July 2002. Final revision September 2004] Summary. A common application of multilevel models is to apportion the variance in the response according to the different levels of the data.Whereas partitioning variances is straight- forward in models with a continuous response variable with a normal error distribution at each level, the extension of this partitioning to models with binary responses or to proportions or counts is less obvious. We describe methodology due to Goldstein and co-workers for appor- tioning variance that is attributable to higher levels in multilevel binomial logistic models. This partitioning they referred to as the variance partition coefficient. We consider extending the vari- ance partition coefficient concept to data sets when the response is a proportion and where the binomial assumption may not be appropriate owing to overdispersion in the response variable. Using the literacy data from the 1991 Indian census we estimate simple and complex variance partition coefficients at multiple levels of geography in models with significant overdispersion and thereby establish the relative importance of different geographic levels that influence edu- cational disparities in India. Keywords: Contextual variation; Illiteracy; India; Multilevel modelling; Multiple spatial levels; Overdispersion; Variance partition coefficient 1. Introduction Multilevel regression models (Goldstein, 2003; Bryk and Raudenbush, 1992) are increasingly being applied in many areas of quantitative research.
    [Show full text]
  • Using Geographically Weighted Poisson Regression for County-Level Crash Modeling in California ⇑ Zhibin Li A,B, , Wei Wang A,1, Pan Liu A,2, John M
    Safety Science 58 (2013) 89–97 Contents lists available at SciVerse ScienceDirect Safety Science journal homepage: www.elsevier.com/locate/ssci Using Geographically Weighted Poisson Regression for county-level crash modeling in California ⇑ Zhibin Li a,b, , Wei Wang a,1, Pan Liu a,2, John M. Bigham b,3, David R. Ragland b,3 a School of Transportation, Southeast University, Si Pai Lou #2, Nanjing 210096, China b Safe Transportation Research and Education Center, Institute of Transportation Studies, University of California, Berkeley, 2614 Dwight Way #7374, Berkeley, CA 94720-7374, United States article info abstract Article history: Development of crash prediction models at the county-level has drawn the interests of state agencies for Received 25 December 2012 forecasting the normal level of traffic safety according to a series of countywide characteristics. A com- Received in revised form 11 March 2013 mon technique for the county-level crash modeling is the generalized linear modeling (GLM) procedure. Accepted 13 April 2013 However, the GLM fails to capture the spatial heterogeneity that exists in the relationship between crash counts and explanatory variables over counties. This study aims to evaluate the use of a Geographically Weighted Poisson Regression (GWPR) to capture these spatially varying relationships in the county-level Keywords: crash data. The performance of a GWPR was compared to a traditional GLM. Fatal crashes and countywide Safety factors including traffic patterns, road network attributes, and socio-demographic characteristics were Crash County-level collected from the 58 counties in California. Results showed that the GWPR was useful in capturing Geographically Weighted Regression the spatially non-stationary relationships between crashes and predicting factors at the county level.
    [Show full text]