IX.2. a Semiconductor Device Primer
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

An Integrated Semiconductor Device Enabling Non-Optical Genome Sequencing
ARTICLE doi:10.1038/nature10242 An integrated semiconductor device enabling non-optical genome sequencing Jonathan M. Rothberg1, Wolfgang Hinz1, Todd M. Rearick1, Jonathan Schultz1, William Mileski1, Mel Davey1, John H. Leamon1, Kim Johnson1, Mark J. Milgrew1, Matthew Edwards1, Jeremy Hoon1, Jan F. Simons1, David Marran1, Jason W. Myers1, John F. Davidson1, Annika Branting1, John R. Nobile1, Bernard P. Puc1, David Light1, Travis A. Clark1, Martin Huber1, Jeffrey T. Branciforte1, Isaac B. Stoner1, Simon E. Cawley1, Michael Lyons1, Yutao Fu1, Nils Homer1, Marina Sedova1, Xin Miao1, Brian Reed1, Jeffrey Sabina1, Erika Feierstein1, Michelle Schorn1, Mohammad Alanjary1, Eileen Dimalanta1, Devin Dressman1, Rachel Kasinskas1, Tanya Sokolsky1, Jacqueline A. Fidanza1, Eugeni Namsaraev1, Kevin J. McKernan1, Alan Williams1, G. Thomas Roth1 & James Bustillo1 The seminal importance of DNA sequencing to the life sciences, biotechnology and medicine has driven the search for more scalable and lower-cost solutions. Here we describe a DNA sequencing technology in which scalable, low-cost semiconductor manufacturing techniques are used to make an integrated circuit able to directly perform non-optical DNA sequencing of genomes. Sequence data are obtained by directly sensing the ions produced by template-directed DNA polymerase synthesis using all-natural nucleotides on this massively parallel semiconductor-sensing device or ion chip. The ion chip contains ion-sensitive, field-effect transistor-based sensors in perfect register with 1.2 million wells, which provide confinement and allow parallel, simultaneous detection of independent sequencing reactions. Use of the most widely used technology for constructing integrated circuits, the complementary metal-oxide semiconductor (CMOS) process, allows for low-cost, large-scale production and scaling of the device to higher densities and larger array sizes. -

Vlsi Design Lecture Notes B.Tech (Iv Year – I Sem) (2018-19)
VLSI DESIGN LECTURE NOTES B.TECH (IV YEAR – I SEM) (2018-19) Prepared by Dr. V.M. Senthilkumar, Professor/ECE & Ms.M.Anusha, AP/ECE Department of Electronics and Communication Engineering MALLA REDDY COLLEGE OF ENGINEERING & TECHNOLOGY (Autonomous Institution – UGC, Govt. of India) Recognized under 2(f) and 12 (B) of UGC ACT 1956 (Affiliated to JNTUH, Hyderabad, Approved by AICTE - Accredited by NBA & NAAC – ‘A’ Grade - ISO 9001:2015 Certified) Maisammaguda, Dhulapally (Post Via. Kompally), Secunderabad – 500100, Telangana State, India Unit -1 IC Technologies, MOS & Bi CMOS Circuits Unit -1 IC Technologies, MOS & Bi CMOS Circuits UNIT-I IC Technologies Introduction Basic Electrical Properties of MOS and BiCMOS Circuits MOS I - V relationships DS DS PMOS MOS transistor Threshold Voltage - VT figure of NMOS merit-ω0 Transconductance-g , g ; CMOS m ds Pass transistor & NMOS Inverter, Various BiCMOS pull ups, CMOS Inverter Technologies analysis and design Bi-CMOS Inverters Unit -1 IC Technologies, MOS & Bi CMOS Circuits INTRODUCTION TO IC TECHNOLOGY The development of electronics endless with invention of vaccum tubes and associated electronic circuits. This activity termed as vaccum tube electronics, afterward the evolution of solid state devices and consequent development of integrated circuits are responsible for the present status of communication, computing and instrumentation. • The first vaccum tube diode was invented by john ambrase Fleming in 1904. • The vaccum triode was invented by lee de forest in 1906. Early developments of the Integrated Circuit (IC) go back to 1949. German engineer Werner Jacobi filed a patent for an IC like semiconductor amplifying device showing five transistors on a common substrate in a 2-stage amplifier arrangement. -
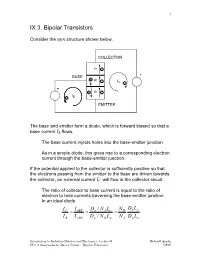
IX.3. a Semiconductor Device Primer – Bipolar Transistors LBNL 2
1 IX.3. Bipolar Transistors Consider the npn structure shown below. COLLECTOR n- BASE + +p -IC- + +n- I -B EMITTER The base and emitter form a diode, which is forward biased so that a base current IB flows. The base current injects holes into the base-emitter junction. As in a simple diode, this gives rise to a corresponding electron current through the base-emitter junction. If the potential applied to the collector is sufficiently positive so that the electrons passing from the emitter to the base are driven towards the collector, an external current IC will flow in the collector circuit. The ratio of collector to base current is equal to the ratio of electron to hole currents traversing the base-emitter junction. In an ideal diode IC I nBE Dn / N ALn N D Dn Lp = = = I B I pBE Dp / N D Lp N A Dp Ln Introduction to Radiation Detctors and Electronics, 13-Apr-99 Helmuth Spieler IX.3. A Semiconductor Device Primer – Bipolar Transistors LBNL 2 If the ratio of doping concentrations in the emitter and base regions ND /NA is sufficiently large, the collector current will be greater than the base current. ⇒ DC current gain Furthermore, we expect the collector current to saturate when the collector voltage becomes large enough to capture all of the minority carrier electrons injected into the base. Since the current inside the transistor comprises both electrons and holes, the device is called a bipolar transistor. Dimensions and doping levels of a modern high-frequency transistor (5 – 10 GHz bandwidth) 0 0.5 1.0 1.5 Distance [µm] (adapted from Sze) Introduction to Radiation Detctors and Electronics, 13-Apr-99 Helmuth Spieler IX.3. -

Laboratory Exercise 2 DC Characteristics of Bipolar Junction
DEPARTMENT OF SEMICONDUCTOR AND OPTOELECTRONIC DEVICES Semiconductor Device Laboratory Laboratory Exercise 2 DC characteristics of Bipolar Junction Transistors (BJT) The aim of the exercise The main aim of this laboratory exercise is to understand principles of operation of Bipolar Junction Transistors (BJT). It covers the measurements of static and small signal parameters. Backgrounds Physical structure of the BJT BJT is a semiconductor device having a three-layer structure with three external electrodes, the emitter (E), the base (B), and the collector (C). As shown in Fig. 1, the structure may be p-n-p or n-p-n type. Despite of the transistor type the emitter layer has always more acceptor or donor impurities added than the base or the collector layer. This asymmetry results from different roles the emitter and the collector layers play in the BJT. In normal operation of the BJT (as an amplifier), the base-emitter junction is forward biased and the base-collector junction is reverse biased. Transistor amplification is controlled by changing the current flow through the base-emitter junction. C N C . C P C . P B. N B. B . B . E . N . E P . E E (a) (b) Fig. 1. The n-p-n BJT (a) and the p-n-p BJT (b) along with their symbols There are three operating configurations of the BJT. These are the common-emitter (OE) configuration, the common-base configuration (OB), and the common-collector (OC) configuration. These configurations are shown in Fig. 2. (a) (b) (c) Fig. 2 The n-p-n transistor operating configurations: (a) common-emitter, (b) common-base, (c) common-collector DC characteristics Four types of characteristics can be defined for each of the transistor operating configurations. -

Field Effect Transistor (FET) Types and Features
Field Effect Transistor (FET) Types and Features Here I’m discussing about the topic FET. FET is another semiconductor device like BJT which can be used as switch, amplifier, resistor etc. FET consists of 3 terminals. Drain(D) Source(S) Gate(G) In these 3 terminals, Gate terminal acts as a controlling terminal. We know that a BJT acts as a current controlling device. Like that, FET also acts as a voltage controlling device. Here, the voltage between gate and source controls the drain current. So, it is called as voltage controlled device. FET Features: FET is more temperature stable compared to BJT It requires less space compared to BJT. So it is used heavily in circuits. FET has higher input impedance. So, it is more useful in amplifiers. Types of FETs: 1. Junction FET 2. MESFET 3. MOSFET Here I am discussing about the topic JFET. Junction FET (JFET): Basically the JFET is classified into 2 types. N-Channel JFET P-Channel JFET N-Channel JFET: When we consider a silicon bar and fabricated n-type at its two ends and heavily doped p-type materials at each side of the bar, the thin region will be remained as observed in figure is channel. Since this channel is in n-type bar this is called as n-channel FET. Here the current is carried by electrons. P-Channel FET: When we consider a silicon bar and fabricated p-type at its two ends and heavily doped n-type materials at each side of the bar, here the thin region remained as observed in figure is channel. -

Csd25301w1015
P-Channel CICLON NexFET™ Power MOSFETs CSD25301W1015 Features Product Summary D D • Ultra Low Qg & Qgd VDS -20 V Q 2.0 nC • Small Footprint g S S Qgd 0.32 nC • Low Profile 0.65mm height VGS= -1.5V 175 mΩ • Pb Free S G RDS(on) VGS=-2.5V 80 mΩ VGS=-4.5V 62 mΩ RoHS Compliant • CSP 1.0 x 1.5 mm Wafer Vth -0.75 V • Halogen Free Level Package Top View o Maximum Values (TA=25 C unless otherwise stated) Symbol Parameter Value Units VDS Drain to Source Voltage -20 V VGS Gate to Source Voltage ±8 V 1 ID Continuous Drain Current, TJ = 25°C -2.2 A IDM Pulsed Drain Current, TJ = 25°C1,2 -8.8 A 1 PD Power Dissipation 1.5 W TJ, TSTG Operating Junction and Storage Temperature Range -55 to 150 °C 0 1. RthJA = 85 C/W on max Cu (2 oz.) on 0.060” thick FR4 PCB 2. Pulse width ≤300 µs, duty cycle ≤ 2% RDS(ON) vs. VGS Gate Charge 300 6 ID = -1A V DS = -10V ) 250 5 ID = -1A Ω T = 125ºC 200 J 4 TJ = 25ºC 150 3 100 (V) Voltage - Gate 2 - On Resistance (m GS -V DS(on) 50 R 1 0 0 0123456 0 0.25 0.5 0.75 1 1.25 1.5 1.75 2 2.25 2.5 -V - Gate to Source Voltage (V) Qg - Gate Charge (nC) GS Ordering Information Type Package Package Media Qty Ship CSD25301W1015 1.0 X 1.5 Wafer Level Package 7 inch reel 3000 Tape and Reel © 2008 CICLON Semiconductor Device Corp., rev 2.3 www.ciclonsemi.com All rights reserved. -

A Review of MOS Device Physics
T. H. Lee Handout #2: EE214 Fall 2003 A Review of MOS Device Physics 1.0 Introduction This chapter focuses attention on those aspects of transistor behavior that are of immediate relevance to the RF circuit designer. Separation of first-order from higher-order phenom- ena is emphasized, so there are many instances when crude approximations are presented in the interest of developing insight. As a consequence, this review is intended as a supple- ment to, rather than a replacement for, traditional rigorous treatments of the subject. In particular, we have to acknowledge that today’s deep-submicron MOSFET is so complex a device that simple equations cannot possibly provide anything other than first-order (maybe even zeroth-order) approximations to the truth. The philosophy underlying this chapter is to convey a simple story to enable first-pass designs, which are then verified by simulators using much more sophisticated models. Qualitative insights developed with the aid of the zeroth-order models enable the designer to react appropriately to bad news from the simulator. We design with a simpler set of models than we use for verification. With that declaration out of the way, we now turn to a little history before launching into a series of derivations. 2.0 A Little History Attempts to create field-effect transistors (FETs) actually predate the development of bipolar devices by over twenty years. In fact, the first patent application for a FET-like transistor was filed in 1926 by Julius Lilienfeld, but he never constructed a working device.1 Before co-inventing the bipolar transistor, William Shockley also tried to modu- late the conductivity of a semiconductor to create a field-effect transistor. -

Bipolar Junction Transistor As a Switch
IOSR Journal of Electrical and Electronics Engineering (IOSR-JEEE) e-ISSN: 2278-1676,p-ISSN: 2320-3331, Volume 13, Issue 1 Ver. I (Jan. – Feb. 2018), PP 52-57 www.iosrjournals.org Bipolar Junction Transistor as a Switch Ali Habeb Aseeri1, Fouzeyah Rajab Ali2 1(Switching Dep, High institute of telecommunication and navigation/PAAET, Kuwait,[email protected]) 2(Switching Dep, High institute of telecommunication and navigation/PAAET, Kuwait,[email protected]) Abstract: Understanding the application of a bipolar Junction transistor or BJT as a switch requiers understanding the general working principles behind a transistor and the specific working principles behind a BJT. A transistor is essentially a semiconductor device with physical properties that make it ideal for amplifying or switching electric current and other signal. At the heart of this device is a doped semiconductor with engineered properties to alter its conductivity for a particular use. A BJT is a type of transistor with two major semiconductor materials that constitute three major areas or regions, each doped according to requirements. This architectural characteristics of a BJT brings forth effective applications in implications or on-off switching operations. Nonetheless, understanding BJT as a switch requires understanding the working principles underneath the device, the functions of each of the three major regions within this transistor, and the role of electron movement or current flow in the switching mechanism Keywords: BJT-collector-emitter-base-collector voltage -

Power Devices and Integrated Circuits Based on 4H-Sic Lateral Jfets
ABSTRACT OF THE DISSERTATION Power Devices and Integrated Circuits Based on 4H-SiC Lateral JFETs By MING SU Dissertation Director Professor Kuang Sheng Dissertation Co-director Professor Jian H. Zhao Silicon carbide (SiC) is a wide-bandgap semiconductor that has drawn significant research interest for the next-generation power electronics due to its superior electrical properties. Excellent device performance has been repeatedly demonstrated by SiC vertical power devices. However, for lateral power devices that offer the unique advantage of possible monolithic integration of a power electronics system-on-chip, the progress has been limited. This dissertation describes the 4H-SiC vertical-channel lateral JFET (VC-LJFET) technology that provides a suitable solution for power integration applications. Power devices based on this structure have a trenched-and-implanted vertical channel and a carefully designed lateral drift region, enabling normally-off operation with a high-voltage blocking capability. Low-voltage (LV) versions of VC-LJFET feature ii nearly identical device structures with a reduced drift length, and can be readily fabricated on the same wafer with the power devices. Essential components for a power integrated circuit, such as gate drive buffers, can be thus implemented monolithically on the VC-LJFET technology platform. This dissertation research starts with the process improvement investigation for the TI-JFET structure. Particularly, a novel ohmic contact scheme is developed using Ni to replace the troubling process in TI-VJFETs. The entire process flow of VC-LJFET is then designed and demonstrated in experiments, leading to the world’s first demonstration of a normally-off lateral power JFET in SiC. -

Sixteen Years After the Passage of the US Semiconductor Chip Protection
SIXTEEN YEARS AFTER THE PASSAGE OF THE U.S. SEMICONDUCTOR CHIP PROTECTION ACT: Is INTERNATIONAL PROTECTION WORKING? By Leon Radomsky ABSTRACT Sixteen years ago, the U.S. Congress passed the Semiconductor Chip Protection Act ("SCPA") in an attempt to provide national protec- tion from chip piracy to U.S. chip manufacturers and encourage interna- tional efforts to reduce chip piracy worldwide. In this Article, the author evaluates the SCPA's effectiveness. The author concludes that the Act has influenced foreign legislation and international treaty provisions, but has provided virtually no real chip protection. Instead, technological ad- vances, market changes, and improvements in industry practice have pro- tected chip manufacturers from chip piracy. Before reaching his conclu- sion, the author describes the origins of the SCPA and gives an overview of the Act, including general provisions and a criticism of the protected subject matter's scope. The author then compares foreign chip protection acts and international chip provisions with the SCPA, arguing that worldwide chip piracy has declined mostly for reasons unrelated to for- eign chip legislation. While changes in technology and the market have mostly rendered chip protection laws obsolete in technologically ad- vanced nations, the author concludes by hinting that such laws might be helpful in less technologically developed nations. TABLE OF CONTENTS I. IN TRODUCTION ..................................................................................................... 1050 II. Sui GENERIS PROTECTION OF SEMICONDUCTOR CHIPS: WHY CONGRESS DEEMED CHIP PROTECTION NECESSARY AND WHY PATENT, COPYRIGHT, AND TRADE SECRET LAWS W ERE INSUFFICIENT .......................................................... 1053 © 2000 Leon Radomsky. t Member, Intellectual Property Group, Foley & Lardner, Washington D.C., spe- cializing in patent law relating to semiconductor processing and materials science tech- nologies. -

Study on Integrated Circuit
STUDY ON INTEGRATED CIRCUIT In electronics, an integrated circuit (also known as IC, microcircuit, microchip, silicon chip, or chip) is a miniaturized electronic circuit (consisting mainly of semiconductor devices, as well as passive components) that has been manufactured in the surface of a thin substrate of semiconductor material. Integrated circuits are used in almost all electronic equipment in use today and have revolutionized the world of electronics. A hybrid integrated circuit is a miniaturized electronic circuit constructed of individual semiconductor devices, as well as passive components, bonded to a substrate or circuit board. This article is about monolithic integrated circuits. Integrated circuits were made possible by experimental discoveries which showed that semiconductor devices could perform the functions of vacuum tubes, and by mid-20th-century technology advancements in semiconductor device fabrication. The integration of large numbers of tiny transistors into a small chip was an enormous improvement over the manual assembly of circuits using discrete electronic components. The integrated circuit's mass production capability, reliability, and building-block approach to circuit design ensured the rapid adoption of standardized ICs in place of designs using discrete transistors. There are two main advantages of ICs over discrete circuits: cost and performance. Cost is low because the chips, with all their components, are printed as a unit by photolithography and not constructed one transistor at a time. Furthermore, much less material is used to construct a circuit as a packaged IC die than as a discrete circuit. Performance is high since the components switch quickly and consume little power (compared to their discrete counterparts), because the components are small and close together. -

Introduction to Solid State Semi- Conductors
Introduction to Solid State Semi- Conductors Course No: E04-009 Credit: 4 PDH A. Bhatia Continuing Education and Development, Inc. 9 Greyridge Farm Court Stony Point, NY 10980 P: (877) 322-5800 F: (877) 322-4774 [email protected] CHAPTER 1 SEMICONDUCTOR DIODES LEARNING OBJECTIVES Learning objectives are stated at the beginning of each chapter. These learning objectives serve as a preview of the information you are expected to learn in the chapter. The comprehensive check questions are based on the objectives. By successfully completing the NRTC, you indicate that you have met the objectives and have learned the information. The learning objective are listed below. Upon completion of this chapter, you should be able to do the following: 1. State, in terms of energy bands, the differences between a conductor, an insulator, and a semiconductor. 2. Explain the electron and the hole flow theory in semiconductors and how the semiconductor is affected by doping. 3. Define the term "diode" and give a brief description of its construction and operation. 4. Explain how the diode can be used as a half-wave rectifier and as a switch. 5. Identify the diode by its symbology, alphanumerical designation, and color code. 6. List the precautions that must be taken when working with diodes and describe the different ways to test them. INTRODUCTION TO SOLID-STATE DEVICES As you recall from previous studies in this series, semiconductors have electrical properties somewhere between those of insulators and conductors. The use of semiconductor materials in electronic components is not new; some devices are as old as the electron tube.