DOCSLIB.ORG

Bipolar Junction Transistor

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Bipolar Junction Transistor EEE 531: Semiconductor Device Theory I Instructor: Dragica Vasileska Department of Electrical Engineering Arizona State University Bipolar Junction Transistor EEE 531: Semiconductor Device Theory I Outline 1. Introduction 2. IV Characteristics of a BJT 3. Breakdown in BJT 4. Geometry Effects in BJT EEE 531: Semiconductor Device Theory I 1. Introduction Original point-contact transistor Inventors of the transistor: (1947) William Shockley, John Bardeen and Walter Brattain First grown transistor (1950) EEE 531: Semiconductor Device Theory I (A) Terminology and symbols PNP - transistor NPN - transistor E C E C B B E p+ n p C E n+ p n C + + V V V V EB CB BE + + BC B B • Both, pnp and npn transistors can be thought as two very closely spaced pn-junctions. • The base must be small to allow interaction between the two pn-junctions. EEE 531: Semiconductor Device Theory I • There are four regions of operation of a BJT transistor (example for a pnp BJT): V EB Forward active region Saturation region (emitter-base FB, collector-base RB) (both junctions forward biased) V CB Cutoff region Inverted active region (both junctions reverse biased) (emitter-base RB, collector-base FB) • Since it has three leads, there are three possible amplifier types: C E p p+ B B E C n V n V p+ n p EC EC V p+ V p V EB CB EB V B CB E C (a) Common-base (b) Common-emitter (c) Common-collector EEE 531: Semiconductor Device Theory I (B) Qualitative description of transistor operation p+ n p • Emitter doping is much larger than I { I Ep Cp base doping • Base doping larger than collector I I En Cn doping • Current components: I I B1 B3 I E I Ep I En I I B2 cn I I I I C Cp Cn E En C I B I E IC I B1 I B2 I B3 • I = current from electrons being bBa1ck injected into the forward-biased E emiter-base junction F E V • I = current due to electrons that reBp2lace the recombined electrons in the base • I = collector current due to I B3 I Cp thermally-generated electrons in the Ep collector that go in the base EEE 531: Semiconductor Device Theory I (C) Circuit definitions Base transport factor : T T ICp / I Ep Ideally it would be equal to unity (recombination in the base reduces its value) Emitter injection efficiency : I I Ep Ep Approaches unity if emitter doping is ICp I Ep I E much larger than base doping Alpha-dc: I I I IC Cp Cn Cp dc T I E I Ep I En I Ep I En Beta-dc: I I C C dc Current gain is large when dc I I I 1 dc B E C dc approaches unity EEE 531: Semiconductor Device Theory I Collector-reverse saturation current: I BC0 ICn IC ICp ICn dc I E I BC0 Collector current in common-emitter configuration: I dc BC0 IC dc IC I B I BC0 IC I B 1 dc 1 dc IC dc I B I EC0 I EC0 1 dc I BC0 Large current gain capability: Small base current I forces the E-B junction to be forward B biased and inject large number of holes which travel through the base to the collector. EEE 531: Semiconductor Device Theory I (D) Types of transistors Base • Discrete (double-diffused) Emitter p+np transistor 5 m 200 m Collector • Integrated-circuit n+pn transistor 6 m 200 m EEE 531: Semiconductor Device Theory I 2. IV-Characteristics of a BJT (A) General Considerations • Approximations made for derivation of the ideal IV-characteristics of a BJT: (1) no recombination in the base quasi-neutral region (2) no generation-recombination in the E-B and C-B depletion regions (3) one-dimensional current flow (4) no external sources • Notation: p+ n p N = N N = N N = N AE E DB B AC C L = L L = L L = L n E p B n C D = D D = D D = D n E p B n C n = n p = p n = n p0 E0 n0 B0 p0 C0 = = = n E p B n C EEE 531: Semiconductor Device Theory I • The carrier concentration variation for various regions of operation is shown below: E-B C-B p (0) B saturation n (0’) C n (0”) E p (W) B Forward p (x) n (x’) B C n (x”) active n E p C0 n B0 E0 p (W) x” B x’ 0” 0 Cut-off W 0’ • Assuming long emitter and collector regions, the solutions of the minority electrons continuity equation in the emitter and collector are of the form: VEB /VT x"/ LE nE (x") nE0 e 1 e VCB /VT x'/ LC nC (x') nC0 e 1 e EEE 531: Semiconductor Device Theory I • For the base region, the steady-state solution of the continuity equation for minority holes, of the form: d 2p p B B 0 2 2 dx LB using the boundary conditions: VEB /VT VCB /VT pB (0) pB0 e 1, pB (W ) pB0 e 1 is given by: sinh(W x) / L V /V p (x) p B e EB T 1 B B0 sinh W / LB sinhx / L V /V p B e CB T 1 B0 sinh W / LB Note: The presence of the sinh() terms means that recombination in the base quasi-neutral region is allowed. EEE 531: Semiconductor Device Theory I • Once we have the variation of n (x”), p (x) and n (x’), we can E B C calculate the corresponding diffusion current components: E-B C-B I =I (0”)+I (0) I =I (0’)+I (W) E nE pB I (0) C nC pB pB I (W) I (0”) pB I (x”) nE I (x) nE pB I (0’) I (x’) nC nC I =I (0)-I (W) x” B2 pB pB x’ 0” 0 W 0’ Base recombination current • Expressions for various diffusion current components: dnE dnC InE (0") AqDE , InC (0') AqDC dx" x"0" dx' x'0' dpB dpB I pB (0) AqDB , I pB (W ) AqDB dx x0 dx xW EEE 531: Semiconductor Device Theory I • Final results for the emitter, base and collector currents: D D 2 E B VEB /VT I E Aqni coth(W / LB ) e 1 LE N E LB N B D 1 2 B VCB /VT Aqni e 1 LB N B sinh(W / LB ) D 1 2 B VEB /VT IC Aqni e 1 LB N B sinh(W / LB ) D D 2 C B VCB /VT Aqni coth(W / LB ) e 1 LC NC LB N B D D 1 2 E B VEB /VT I B Aqni coth(W / LB ) e 1 LE N E LB N B sinh(W / LB ) D D 1 2 C B VCB /VT Aqni coth(W / LB ) e 1 LC NC LB N B sinh(W / LB ) EEE 531: Semiconductor Device Theory I • For short-base diodes, for which W/L <<1, we have: B x2 1 x cosh(x) 1 ; sinh(x) x; coth(x) 2 sinh(x) 2 • Therefore, for short-base diodes, the base current simplifies to: I I B1 B2 D DW 2 E B VEB /VT I B Aqni e 1 LE N E LB N B 2LB D D W 2 C B VCB /VT Aqni e 1 LC NC LB N B 2LB -I I B3 B2 • As W/L 0 (or ), the recombination base current I 0 . B B B2 EEE 531: Semiconductor Device Theory I (B) Current expressions for different biasing regimes Forward-active region: • E-B junction is forward biased, C-B junction is reverse- biased: D D 2 E B VEB /VT I E Aqni coth(W / LB )e I En I Ep LE N E LB N B D 1 2 B VEB /VT IC Aqni e ICp LB N B sinh(W / LB ) D D cosh(W / L ) 1 2 E B B VEB /VT I B Aqni e LE N E LB N B sinh(W / LB ) 2 DC DB cosh(W / LB ) 1 Aqni L N L N sinh(W / L ) C C B B B These terms vanish if there is no recombi- EEE 531: Semiconductor Device Theory I nation in the base • Graphical description of various current components: p+ n p I { }I I Ep Cp I E C I { I En Cn I I Recombination in the base B1 B3 I is ignored in this diagram. B • The emitter injection efficiency is given by: L N D L N D E E B coth(W / L ) E E B I L N D B WN D Ep B B E B E L N D short L N D I Ep I En E E B E E B 1 coth(W / LB ) base 1 LB N B DE WN B DE EEE 531: Semiconductor Device Theory I • The base transport factor is given by: I 1 W 2 Cp 1 T I cosh(W /L ) short 2L2 Ep B base B • Common-emitter current gain: L N D E E B coth(W / L ) L N D B L N D B B E E E B dc L N D short E E B 2 WNBDE 1 2 coth(W / LB )sinh (W /2LB ) base LBNBDE G = WN (Gummel number) B B • For a more general case of a non-uniform doping in the base, the Gummel number is given by: W G N (x)dx Typical values of G : B B B 0 EEE 531: Semiconductor Device Theory I Saturation region: • E-B and C-B junctions are both forward biased: D D 2 E B VEB /VT I E Aqni coth(W / LB )e LE N E LB N B D 2 B VCB /VT Aqni coth(W / LB )e I En I Ep - I Ep' LB N B D 1 2 B VEB /VT IC Aqni e LB N B sinh(W / LB ) D D 2 C B VCB /VT Aqni coth(W / LB )e ICp ICn ICp' LC NC LB N B I B I E IC Base current much larger than in forward-active regime ICn I B3 EEE 531: Semiconductor Device Theory I • Graphical description of various current components: p+ n p I { }I I Ep Cp I E C I ’{ } I ’ Ep Cp I I En { Cn I I Recombination in the base B1 B3 I is ignored in this diagram.
Load more

Recommended publications
  • Chapter 7: AC Transistor Amplifiers
    Chapter 7: Transistors, part 2 Chapter 7: AC Transistor Amplifiers The transistor amplifiers that we studied in the last chapter have some serious problems for use in AC signals. Their most serious shortcoming is that there is a “dead region” where small signals do not turn on the transistor. So, if your signal is smaller than 0.6 V, or if it is negative, the transistor does not conduct and the amplifier does not work. Design goals for an AC amplifier Before moving on to making a better AC amplifier, let’s define some useful terms. We define the output range to be the range of possible output voltages. We refer to the maximum and minimum output voltages as the rail voltages and the output swing is the difference between the rail voltages. The input range is the range of input voltages that produce outputs which are not at either rail voltage. Our goal in designing an AC amplifier is to get an input range and output range which is symmetric around zero and ensure that there is not a dead region. To do this we need make sure that the transistor is in conduction for all of our input range. How does this work? We do it by adding an offset voltage to the input to make sure the voltage presented to the transistor’s base with no input signal, the resting or quiescent voltage , is well above ground. In lab 6, the function generator provided the offset, in this chapter we will show how to design an amplifier which provides its own offset.
    [Show full text]
  • Basic DC Motor Circuits
    Basic DC Motor Circuits Living with the Lab Gerald Recktenwald Portland State University [email protected] DC Motor Learning Objectives • Explain the role of a snubber diode • Describe how PWM controls DC motor speed • Implement a transistor circuit and Arduino program for PWM control of the DC motor • Use a potentiometer as input to a program that controls fan speed LWTL: DC Motor 2 What is a snubber diode and why should I care? Simplest DC Motor Circuit Connect the motor to a DC power supply Switch open Switch closed +5V +5V I LWTL: DC Motor 4 Current continues after switch is opened Opening the switch does not immediately stop current in the motor windings. +5V – Inductive behavior of the I motor causes current to + continue to flow when the switch is opened suddenly. Charge builds up on what was the negative terminal of the motor. LWTL: DC Motor 5 Reverse current Charge build-up can cause damage +5V Reverse current surge – through the voltage supply I + Arc across the switch and discharge to ground LWTL: DC Motor 6 Motor Model Simple model of a DC motor: ❖ Windings have inductance and resistance ❖ Inductor stores electrical energy in the windings ❖ We need to provide a way to safely dissipate electrical energy when the switch is opened +5V +5V I LWTL: DC Motor 7 Flyback diode or snubber diode Adding a diode in parallel with the motor provides a path for dissipation of stored energy when the switch is opened +5V – The flyback diode allows charge to dissipate + without arcing across the switch, or without flowing back to ground through the +5V voltage supply.
    [Show full text]
  • An Integrated Semiconductor Device Enabling Non-Optical Genome Sequencing
    ARTICLE doi:10.1038/nature10242 An integrated semiconductor device enabling non-optical genome sequencing Jonathan M. Rothberg1, Wolfgang Hinz1, Todd M. Rearick1, Jonathan Schultz1, William Mileski1, Mel Davey1, John H. Leamon1, Kim Johnson1, Mark J. Milgrew1, Matthew Edwards1, Jeremy Hoon1, Jan F. Simons1, David Marran1, Jason W. Myers1, John F. Davidson1, Annika Branting1, John R. Nobile1, Bernard P. Puc1, David Light1, Travis A. Clark1, Martin Huber1, Jeffrey T. Branciforte1, Isaac B. Stoner1, Simon E. Cawley1, Michael Lyons1, Yutao Fu1, Nils Homer1, Marina Sedova1, Xin Miao1, Brian Reed1, Jeffrey Sabina1, Erika Feierstein1, Michelle Schorn1, Mohammad Alanjary1, Eileen Dimalanta1, Devin Dressman1, Rachel Kasinskas1, Tanya Sokolsky1, Jacqueline A. Fidanza1, Eugeni Namsaraev1, Kevin J. McKernan1, Alan Williams1, G. Thomas Roth1 & James Bustillo1 The seminal importance of DNA sequencing to the life sciences, biotechnology and medicine has driven the search for more scalable and lower-cost solutions. Here we describe a DNA sequencing technology in which scalable, low-cost semiconductor manufacturing techniques are used to make an integrated circuit able to directly perform non-optical DNA sequencing of genomes. Sequence data are obtained by directly sensing the ions produced by template-directed DNA polymerase synthesis using all-natural nucleotides on this massively parallel semiconductor-sensing device or ion chip. The ion chip contains ion-sensitive, field-effect transistor-based sensors in perfect register with 1.2 million wells, which provide confinement and allow parallel, simultaneous detection of independent sequencing reactions. Use of the most widely used technology for constructing integrated circuits, the complementary metal-oxide semiconductor (CMOS) process, allows for low-cost, large-scale production and scaling of the device to higher densities and larger array sizes.
    [Show full text]
  • Chapter Iii Power Bipolar Junction Transistor (Bjt)
    50 CHAPTER III POWER BIPOLAR JUNCTION TRANSISTOR (BJT) 3.1 INTRODUCTION Switching time and switching losses are primary concerns in high power applications. These two factors can significantly influence the frequency of operation and the efficiency of the circuit. Ideally, a high power switch should be able to turn-on and turn-off controllably and with minimum switching loss. The Bipolar junction transistor is an important power semiconductor device used as a switch in a wide variety of applications. The switching speed of a BJT is often limited by the excess minority charge storage in the base and collector regions of the transistor during the saturation state. The conventional methods for improving the switching frequency by reducing the lifetime of the lightly doped collector region through incorporation of impurities such as Au, Pt or by introducing radiation-induced defects have been found unsuitable for high voltage devices due to increased leakage, soft breakdown and high ‘ON’ state voltage [27]. Among the techniques proposed to overcome these problems, use of universal contact (UC) [2, 14] is particularly promising. The present work looks in detail at the various aspects arising out of incorporation of UC in BJTs. The UC is incorporated in the transistor by creating additional diffused regions in an otherwise conventional transistor. These diffused regions influence the minority carrier distribution, nature of minority current flow and also some other parameter such as VCE(sat). To study these phenomena, 51 an analytical model is developed and is utilized to understand the effect of universal contact on reverse recovery, VCE(sat) and other related issues.
    [Show full text]
  • Vlsi Design Lecture Notes B.Tech (Iv Year – I Sem) (2018-19)
    VLSI DESIGN LECTURE NOTES B.TECH (IV YEAR – I SEM) (2018-19) Prepared by Dr. V.M. Senthilkumar, Professor/ECE & Ms.M.Anusha, AP/ECE Department of Electronics and Communication Engineering MALLA REDDY COLLEGE OF ENGINEERING & TECHNOLOGY (Autonomous Institution – UGC, Govt. of India) Recognized under 2(f) and 12 (B) of UGC ACT 1956 (Affiliated to JNTUH, Hyderabad, Approved by AICTE - Accredited by NBA & NAAC – ‘A’ Grade - ISO 9001:2015 Certified) Maisammaguda, Dhulapally (Post Via. Kompally), Secunderabad – 500100, Telangana State, India Unit -1 IC Technologies, MOS & Bi CMOS Circuits Unit -1 IC Technologies, MOS & Bi CMOS Circuits UNIT-I IC Technologies Introduction Basic Electrical Properties of MOS and BiCMOS Circuits MOS I - V relationships DS DS PMOS MOS transistor Threshold Voltage - VT figure of NMOS merit-ω0 Transconductance-g , g ; CMOS m ds Pass transistor & NMOS Inverter, Various BiCMOS pull ups, CMOS Inverter Technologies analysis and design Bi-CMOS Inverters Unit -1 IC Technologies, MOS & Bi CMOS Circuits INTRODUCTION TO IC TECHNOLOGY The development of electronics endless with invention of vaccum tubes and associated electronic circuits. This activity termed as vaccum tube electronics, afterward the evolution of solid state devices and consequent development of integrated circuits are responsible for the present status of communication, computing and instrumentation. • The first vaccum tube diode was invented by john ambrase Fleming in 1904. • The vaccum triode was invented by lee de forest in 1906. Early developments of the Integrated Circuit (IC) go back to 1949. German engineer Werner Jacobi filed a patent for an IC like semiconductor amplifying device showing five transistors on a common substrate in a 2-stage amplifier arrangement.
    [Show full text]
  • Download Technical Paper
    TECHNICAL PAPER Thermal and Electrical Breakdown Versus Reliability of Ta2O5 under Both – Bipolar Biasing Conditions P. Vašina, T. Zedníček, Z. Sita AVX Czech Republic, s.r.o., Dvorakova 328, 563 01 Lanskroun, Czech Republic J. Sikula and J. Pavelka CNRL TU Brno, Technicka 8, 602 00 Brno, Czech Republic Abstract: Our investigation of breakdown is mainly oriented to find a basic parameters describing the phenomena as well as its impact on reliability and quality of the final product that is “GOOD” tantalum capacitor. Basically, breakdown can be produced by a number of successive processes: thermal breakdown because of increasing conductance by Joule heating, avalanche and field emission break, an electromechanical collapse due to the attractive forces between electrodes electrochemical deterioration, dendrite formation and so on. Breakdown causes destruction in the insulator and across the electrodes mainly by melting and evaporation, sometimes followed by ignition. An identification of breakdown nature can be achieved from VA characteristics. Therefore, we have investigated the operating parameters both in the normal mode, Ta is a positive electrode, as well as in the reverse mode with Ta as a negative one. In the reverse mode we have reported that the thermal breakdown is initiated by an increase of the electrical conductance by Joule heating. Consequently followed in a feedback cycle consisting of temperature - conductivity - current - Joule heat - temperature. In normal mode an electrical breakdown can be stimulated by an increase of the electrical conductance in a channel by an electrical pulse and stored charge leads to the sample destruction. Both of these breakdowns have got a stochastic behaviour and could be hardly localized in advance.
    [Show full text]
  • ECE 255, Diodes and Rectifiers
    ECE 255, Diodes and Rectifiers 23 January 2018 In this lecture, we will discuss the use of Zener diode as voltage regulators, diode as rectifiers, and as clamping circuits. 1 Zener Diodes In the reverse biased operation, a Zener diode displays a voltage breakdown where the current rapidly increases within a small range of voltage change. This property can be used to limit the voltage within a small range for a large range of current. The symbol for a Zener diode is shown in Figure 1. Figure 1: The symbol for a Zener diode under reverse biased (Courtesy of Sedra and Smith). Figure 2 shows the i-v relation of a Zener diode near its operating point where the diode is in the breakdown regime. The beginning of the breakdown point is labeled by the current IZK also called the knee current. The oper- ating point can be approximated by an incremental resistance, or dynamic resistance described by the reciprocal of the slope of the point. Since the slope, dI proportional to dV , is large, the incremental resistance is small, generally on the order of a few ohms to a few tens of ohms. The spec sheet usually gives the voltage of the diode at a specified test current IZT . Printed on March 14, 2018 at 10 : 29: W.C. Chew and S.K. Gupta. 1 Figure 2: The i-v characteristic of a Zener diode at its operating point Q (Cour- tesy of Sedra and Smith). The diode can be fabricated to have breakdown voltage of a few volts to a few hundred volts.
    [Show full text]
  • IX.3. a Semiconductor Device Primer – Bipolar Transistors LBNL 2
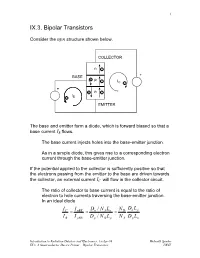
    1 IX.3. Bipolar Transistors Consider the npn structure shown below. COLLECTOR n- BASE + +p -IC- + +n- I -B EMITTER The base and emitter form a diode, which is forward biased so that a base current IB flows. The base current injects holes into the base-emitter junction. As in a simple diode, this gives rise to a corresponding electron current through the base-emitter junction. If the potential applied to the collector is sufficiently positive so that the electrons passing from the emitter to the base are driven towards the collector, an external current IC will flow in the collector circuit. The ratio of collector to base current is equal to the ratio of electron to hole currents traversing the base-emitter junction. In an ideal diode IC I nBE Dn / N ALn N D Dn Lp = = = I B I pBE Dp / N D Lp N A Dp Ln Introduction to Radiation Detctors and Electronics, 13-Apr-99 Helmuth Spieler IX.3. A Semiconductor Device Primer – Bipolar Transistors LBNL 2 If the ratio of doping concentrations in the emitter and base regions ND /NA is sufficiently large, the collector current will be greater than the base current. ⇒ DC current gain Furthermore, we expect the collector current to saturate when the collector voltage becomes large enough to capture all of the minority carrier electrons injected into the base. Since the current inside the transistor comprises both electrons and holes, the device is called a bipolar transistor. Dimensions and doping levels of a modern high-frequency transistor (5 – 10 GHz bandwidth) 0 0.5 1.0 1.5 Distance [µm] (adapted from Sze) Introduction to Radiation Detctors and Electronics, 13-Apr-99 Helmuth Spieler IX.3.
    [Show full text]
  • Laboratory Exercise 2 DC Characteristics of Bipolar Junction
    DEPARTMENT OF SEMICONDUCTOR AND OPTOELECTRONIC DEVICES Semiconductor Device Laboratory Laboratory Exercise 2 DC characteristics of Bipolar Junction Transistors (BJT) The aim of the exercise The main aim of this laboratory exercise is to understand principles of operation of Bipolar Junction Transistors (BJT). It covers the measurements of static and small signal parameters. Backgrounds Physical structure of the BJT BJT is a semiconductor device having a three-layer structure with three external electrodes, the emitter (E), the base (B), and the collector (C). As shown in Fig. 1, the structure may be p-n-p or n-p-n type. Despite of the transistor type the emitter layer has always more acceptor or donor impurities added than the base or the collector layer. This asymmetry results from different roles the emitter and the collector layers play in the BJT. In normal operation of the BJT (as an amplifier), the base-emitter junction is forward biased and the base-collector junction is reverse biased. Transistor amplification is controlled by changing the current flow through the base-emitter junction. C N C . C P C . P B. N B. B . B . E . N . E P . E E (a) (b) Fig. 1. The n-p-n BJT (a) and the p-n-p BJT (b) along with their symbols There are three operating configurations of the BJT. These are the common-emitter (OE) configuration, the common-base configuration (OB), and the common-collector (OC) configuration. These configurations are shown in Fig. 2. (a) (b) (c) Fig. 2 The n-p-n transistor operating configurations: (a) common-emitter, (b) common-base, (c) common-collector DC characteristics Four types of characteristics can be defined for each of the transistor operating configurations.
    [Show full text]
  • The Transistor, Fundamental Component of Integrated Circuits
    D The transistor, fundamental component of integrated circuits he first transistor was made in (SiO2), which serves as an insulator. The transistor, a name derived from Tgermanium by John Bardeen and In 1958, Jack Kilby invented the inte- transfer and resistor, is a fundamen- Walter H. Brattain, in December 1947. grated circuit by manufacturing 5 com- tal component of microelectronic inte- The year after, along with William B. ponents on the same substrate. The grated circuits, and is set to remain Shockley at Bell Laboratories, they 1970s saw the advent of the first micro- so with the necessary changes at the developed the bipolar transistor and processor, produced by Intel and incor- nanoelectronics scale: also well-sui- the associated theory. During the porating 2,250 transistors, and the first ted to amplification, among other func- 1950s, transistors were made with sili- memory. The complexity of integrated tions, it performs one essential basic con (Si), which to this day remains the circuits has grown exponentially (dou- function which is to open or close a most widely-used semiconductor due bling every 2 to 3 years according to current as required, like a switching to the exceptional quality of the inter- “Moore's law”) as transistors continue device (Figure). Its basic working prin- face created by silicon and silicon oxide to become increasingly miniaturized. ciple therefore applies directly to pro- cessing binary code (0, the current is blocked, 1 it goes through) in logic cir- control gate cuits (inverters, gates, adders, and memory cells). The transistor, which is based on the switch source drain transport of electrons in a solid and not in a vacuum, as in the electron gate tubes of the old triodes, comprises three electrodes (anode, cathode and gate), two of which serve as an elec- transistor source drain tron reservoir: the source, which acts as the emitter filament of an electron gate insulator tube, the drain, which acts as the col- source lector plate, with the gate as “control- gate drain ler”.
    [Show full text]
  • Fundamentals of MOSFET and IGBT Gate Driver Circuits
    Application Report SLUA618A–March 2017–Revised October 2018 Fundamentals of MOSFET and IGBT Gate Driver Circuits Laszlo Balogh ABSTRACT The main purpose of this application report is to demonstrate a systematic approach to design high performance gate drive circuits for high speed switching applications. It is an informative collection of topics offering a “one-stop-shopping” to solve the most common design challenges. Therefore, it should be of interest to power electronics engineers at all levels of experience. The most popular circuit solutions and their performance are analyzed, including the effect of parasitic components, transient and extreme operating conditions. The discussion builds from simple to more complex problems starting with an overview of MOSFET technology and switching operation. Design procedure for ground referenced and high side gate drive circuits, AC coupled and transformer isolated solutions are described in great details. A special section deals with the gate drive requirements of the MOSFETs in synchronous rectifier applications. For more information, see the Overview for MOSFET and IGBT Gate Drivers product page. Several, step-by-step numerical design examples complement the application report. This document is also available in Chinese: MOSFET 和 IGBT 栅极驱动器电路的基本原理 Contents 1 Introduction ................................................................................................................... 2 2 MOSFET Technology ......................................................................................................
    [Show full text]
  • Capacitors and Dielectrics Dielectric - a Non-Conducting Material (Glass, Paper, Rubber….)
    Capacitors and Dielectrics Dielectric - A non-conducting material (glass, paper, rubber….) Placing a dielectric material between the plates of a capacitor serves three functions: 1. Maintains a small separation between the plates 2. Increases the maximum operating voltage between the plates. 3. Increases the capacitance In order to prove why the maximum operating voltage and capacitance increases we must look at an atomic description of the dielectric. For now we will show that the capacitance increases by looking at an experimental result: Experiment Since VVCCoo, then Since Q is the same: Coo V CV C V o K CVo C K Dielectric Constant Co Since C > Co , then K > 1 C kCo V V o k kvacuum = 1 (vacuum) k = 1.00059 (air) kglass = 5-10 Material Dielectric Constant k Dielectric Strength (V/m) Air 1.00054 3 Paper 3.5 16 Pyrex glass 4.7 14 A real dielectric is not a perfect insulator and thus you will always have some leakage current between the plates of the capacitor. For a parallel-plate capacitor: C kCo kA C o d From this equation it appears that C can be made as large as possible by decreasing d and thus be able to store a very large amount of charge or equivalently a very large amount of energy. Is there a limit on how much charge (energy) a capacitor can store? YES!! +q K e- - F =qE E e e- E dielectric -q As charge ‘q’ is added to the capacitor plates, the E-field will increase until the dielectric becomes a conductor (dielectric breakdown).
    [Show full text]