THE DIFFERENT DIMENSIONS of WHERE Anupama
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Pidilite Industries Limited Investment Ka Majboot Jod Viewpoint
Pidilite Industries Limited Investment ka majboot jod Viewpoint Pidilite Industries Limited (Pidilite) is India’s market leader in adhesives and Sector: Consumer Goods sealants, construction chemicals, hobby colours and polymer emulsions New Idea in India. Its flagship brands - Fevicol and M-Seal have a market share of ~70% each in the domestic market. With a slew of new launches under Change existing brands and entry into consumer-based categories well supported by adequate media activities, Pidilite has transitioned its target markets View: Positive from industrial users to consumers through effective communication, which has helped the company to register itself in the minds of all its customers. CMP: Rs. 1,476 Revenues grew at a CAGR of 10% over FY2015-19. Though FY2021 is Upside potential: 18-20% expected to be lull affected by Covid-19 pandemic, the growth is expected to come back on track in FY2022 driven by recovery in refurbishment of house/ á Upgrade No change â Downgrade construction activities. Further, expected increase in demand for adhesive products in global markets such as South East Asia, Europe, North America and Latin America post the normalisation of business environment would Company details add to overall revenues in FY2022 and FY2023. A fall in prices of key inputs such as Vinyl Acetate Monomer (VAM) by ~30% in last three quarters will Market cap: Rs. 74,982 cr be a blessing in disguise amid the pandemic. Gross margins have improved by 377 bps in 9MFY2020 to 52.8% and if VAM prices continue to correct in 52-week high/low: Rs. -

PIDILITE INDUSTRIES Adhesive Growth: Ties That Bind
INITIATING COVERAGE PIDILITE INDUSTRIES Adhesive growth: Ties that bind India Equity Research| Consumer Goods Pidilite (PIDI ) is a high quality niche consumption play imbued with strong EDELWEISS 4D RATINGS brand equity in under penetrated and high growth categories. The Absolute Rating BUY company has sustained its dominant position (Fevicol, M-seal have ~70% Rating Relative to Sector Performer market share) by virtue of direct reach to influencers/end users, Risk Rating Relative to Sector Medium successful brand extensions, innovation spurred by robust R&D, out-of- Sector Relative to Market Overweight the-box and catchy ads, acquisitions (ROFF, Mseal, Sargent Art, Hobby Ideas), limited competition and widespread distribution. Key risk/concerns are performance of its international portfolio (especially MARKET DATA (R: PIDI.BO, B: PIDI IN) Brazil) and the Elastomer project. We expect 17% revenue CAGR with CMP : INR 294 Target Price : INR 357 robust 20% PAT CAGR over FY14-16E. We initiate coverage with ‘BUY’. 52-week range (INR) : 304 / 206 Share in issue (mn) : 509.8 Consumer business will continue to sizzle M cap (INR bn/USD mn) : 151 / 2,425 Robust growth across segments spurred PIDI’s consumer & bazaar products (CBP) and Avg. Daily Vol.BSE/NSE(‘000) : 280.0 industrial chemicals segments to post 19% and 14% CAGR, respectively, over FY08-13. Though we expect the CBP business to maintain growth momentum, the industrial SHARE HOLDING PATTER N (%) chemicals business may grow at a slower pace (11.5% CAGR) over FY14-16E due to the Current Q1FY14 Q4FY13 economic slowdown. Overseas business (has been a drag) margins are likely to improve Promoters * 70.1 70.1 70.1 riding sales pick up (Bangladesh, Thailand fastest growth engines), effective MF's, FI's & BK’s 5.3 5.4 5.6 management changes, price hikes and mix improvement. -

India Construction Materials Database of Embodied Energy and Global
DRAFTIndia Construction Materials Database of Embodied Energy and Global Environmental Indicators for Materials Warming Potential Methodology & Results VersionMETHODOLOGY 1.0 REPORT NOVEMBER 30, 2017 Strictly Not for Public Distribution In partnership with European Union European Union Page intentionally left blank Co-Funded by the European Union 2 ABOUT IFC IFC, a member of the World Bank Group, is the largest global development institution focused on the private sector in emerging markets. Working with more than 2,000 businesses worldwide, we use our capital, expertise, and influence to create markets and opportunities in the toughest areas of the world. In FY17, we delivered a record $19.3 billion in long-term financing for developing countries, leveraging the power of the private sector to help end poverty and boost shared prosperity. For more information, visit www.ifc.org DISCLAIMER The material in this work is copyrighted. Copying and/or transmitting portions or all of this work without permission may be a violation of applicable law. IFC encourages dissemination of its work and will normally grant permission to reproduce portions of the work promptly, and when the reproduction is for educational and non-commercial purposes, without a fee, subject to such attributions and notices as we may reasonably require. This database was developed by thinkstep on behalf of IFC for the Eco-cities in India program. This multi-year climate-change focused program is supported by the European Union. IFC does not guarantee the accuracy, reliability, or completeness of the content included in this work, or for the conclusions or judgments described herein, and accepts no responsibility or liability for any omissions or errors (including, without limitation, typographical errors and technical errors) in the content whatsoever or for reliance thereon. -

2016 White Page Consulting Pvt
MOST ADMIRED BRANDS & LEADERS Volume II www.admiredbrand.com Chief Patron Prof. Malcolm McDonald Editor-in-Chief Dhruv Bhatia Chief Operating Officer Sarmad Zargar Regional Head - Asia Asif Var Director - Research M.Y. Makky Director - Corporate Communications Kriti Nagia Head - Digital Media Shahid Bhat General Manager - Strategic Alliances & Partnerships White Page International Anubha Garg Editorial Advisors White Page International is a global consulting firm with a diverse What drives their business is the zeal to make clients successful by portfolio that includes brand consulting, print advertising, creative making the most informed decisions possible. The research conducted Sadiq Zafar - India & South East Asia advertorial promotions, PR and research. The goal is to create a by White Page, is supported by R&D on the latest industry trends and Yasir Yousuf - GCC substantial and lasting improvement in the performance of its clients leading analytical techniques. The expertise lies in performing complex and strengthening their brand value. We serve to accomplish the studies analyzing data and interpreting results leading to most goals of the brand for their products and services in the form business informed decisions through tools like Brand & Consumer Research- Client Servicing journalism and PR. With more and more brands turning to marketing Industry Research- Trade Researches Case Studies & White Papers. Indian Sub-Continent: Prasoon Jha, Danish Malik content, we leverage paid channels like advertorials and social media Southeast Asia: Taye Bayewood, Charlie Zeng, Sonia Khat- coverage for optimum coverage. • Brand and Consumer Research: wani White Page aims to be the world’s leading consulting firm, this is what Provide strategic insight into market entry strategy development, GCC Nations: Muneeb Hussain, Abdullah Al Zaim drives its focus and efforts to be the ideal partner for its clients. -

Simi Sabhaney Kirthiga Reddy Doing the Rex Why Indian Football Should
May 1-15, 2014 Volume 2, Issue 23 `100 Why Indian football should take heart from the launch of the Indian Super League. 20 Subscriber copy not for resale 29 14 31 PLUS VODAFONE ZOOZOOS At it Again 6 AMBUJA CEMENT Shattering Walls 12 MIRCHI KAAN AWARDS DEFINING MOMENTS DUREX INTERVIEW Scarecrow Rules 28 Simi Sabhaney Doing the Rex Kirthiga Reddy FLIPKART Dentsu’s CEO is ready to This digital film is a big hit Facebook India’s head on explore the unknown. on social media. advertisers and India. Shopping Outdoors 30 EDITORIAL This fortnight... Volume 2, Issue 23 e got an insight into the plight of Indian football in the most unexpected way EDITOR Wlast week. A colleague wanted to buy a photograph of Indian players from one Sreekant Khandekar May 1-15, 2014 Volume 2, Issue 23 `100 of the stock image libraries. They couldn’t find one. And when they did find pictures PUBLISHER Prasanna Singh of Indian players playing football it wasn’t what they had in mind: these were images DEPUTY EDITOR of cricketer Mahendra Singh Dhoni and others relaxing with football! But pictures of Ashwini Gangal the Indian football team at play? None that we could find. SENIOR LAYOUT ARTIST Vinay Dominic India’s international performance in football is a bit of a joke. It reached its peak PRODUCTION EXECUTIVE in the 1950s and 1960s and the Indian team even emerged at No 4 in the 1956 Andrias Kisku Olympics. There has been embarrassingly little to say since. In a number of states, ADVERTISING ENQUIRIES among them West Bengal, Kerala, Goa and the North East, football is hugely Naveen Arora, (0120) 4077803, 4077866 Why Indian football should take heart from the Noida launch of the Indian Super League. -

Fevicol Membrane Adhesive Lc
OFFICIAL PUBLICATION ► 80000+ Volume No 17 Issue No 3 Nov 2016 - Jan 2017 20.00 Quarterly Magazine - Pages 76 We Provide Consultancy to Make Beautiful Furniture WE PROVIDE GUIDANCE & EXPERTISE to CONVERT LOGS & LUMBER to SOLID WOOD FURNITURE, PANELS to MODULAR FURNITURE WOOD WASTE to GIFTS & NOVELTIES MODERN WOODWORK AUGUST 2015 MODERN WOODWORK JANUARY - FEBRUARY 2015 - FEBRUARY MODERN WOODWORK JANUARY [email protected] / www.woodconconsultants.com 1 v LT15 Sawmill upgrade for less! The LT15 is now available for only 12,999 USD! more productivity This price includes Setworks, Power feed, 20 blades, a full blade maintenance package, more power plus shipment from Europe to a India seaport! It has NEVER been a better time economical to upgrade your sawmill! SPECIFICATIONS: - 11 kW electric motor - SW Setworks - Power feed - 3 log clamps + 6 side supports - Cuts logs up to 5.4 metres long & 70 cm in diameter 20 bmst50 wood-mizer blade sharpener/setter blades & cbn grinding wheel intro usd price: 12999 / - cif india seaport The Wood-Mizer advantage: TO ORDER: Bobby Ruban Joseph, • Thin-kerf blades cheaper to buy & maintain and more yield from every log Wood-Mizer India Country Manager • Powerful, but less energy consumption lowers your energy bill Phone: +91-98471 69999 • Better timber timber sizes are consistent, and the surface nish is smooth Email: [email protected] • Higher quality sawmills are made in Europe to the highest standards MODERN WOODWORK JANUARY - FEBRUARY 2015 - FEBRUARY MODERN WOODWORK JANUARY for more great quotes on economical sawmills, industrial resaws, and wide band sawmills, visit our new website 2 www.woodmizerasia.com MODERN WOODWORK JANUARY - FEBRUARY 2015 - FEBRUARY MODERN WOODWORK JANUARY 3 CONTENTS NOVEMBER- 2016 - JANUARY 2017 Vol. -
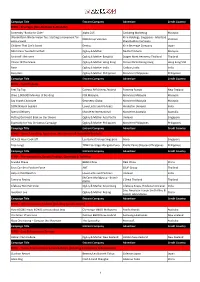
Untitled Spreadsheet
Campaign Title Entrant Company Advertiser Credit Country EFP01 - Beverages (Non-Alcoholic & Alcoholic) Somersby "Books for Cider" Alpha 245 Carlsberg Marketing Malaysia Wonderfarm Wintermelon Tea: Starting a movement for Kirin Holdings, Singapore - Interfood DDB Group Vietnam Vietnam sales growth Shareholding Company Children That Can’t Sweat Dentsu Kirin Beverage Company Japan MILO Cans Twisted Football Ogilvy & Mather Nestle Products Malaysia Smirnoff : Reinvent Ogilvy & Mather Bangkok Diageo Moet Hennessy Thailand Thailand Chivas 18 The Scene Ogilvy & Mather Hong Kong Pernod Ricard Hong Kong Hong Kong SAR Race Ogilvy & Mather India Cadbury India India Recyclass Ogilvy & Mather Philippines Mondelez Philippines Philippines Campaign Title Entrant Company Advertiser Credit Country EFP02 - Food Products Feel Tip Top Colenso BBDO New Zealand Fonterra Brands New Zealand Oreo 1,000,000 Minutes of Bonding FCB Malaysia Mondelez Malaysia Malaysia Say It with Chocolate Geometry Global Mondelez Malaysia Malaysia 100% Natural Seeded Lowe Lintas and Partners Hindustan Unilever India Special Delivery Mondelez International Mondelez Australia Australia Putting Our Heart Back on Our Sleeve Ogilvy & Mather Asia Pacific Unilever Singapore Especially for You Christmas Campaign Ogilvy & Mather Philippines Mondelez Philippines Philippines Campaign Title Entrant Company Advertiser Credit Country EFP03 - Home Furnishing, Appliances, Maintenance & Household Products IKEA 25 Hour Cook Off Leo Burnett Group Singapore Ikano Singapore Tree Lungs TBWA Santiago Mangada -

Coconut Craft
Coconut Craft Contents 1. Introduction 2. Regions of Production 3. Producer Communities 4. Raw Materials 4.1. Coconut shell craft 4.2. Coconut wood craft 5. Tools 6. Process 6.1. Coconut shell craft 6.2. Coconut Wood Craft 7. Uses of the Product 8. Miscellaneous 8.1. Primary market 8.2. Changes in the craft 9. References 1. Introduction The craft of making decorative and utility products out of coconut shell and wood is mostly practiced in parts of India where coconut is grown in abundance. However in most of these areas coconut wood was or is still used as firewood and/or building material. Coconut shell has always been used as a cooking fuel and to make small multiple-utility bowls or serving spoons with simple bamboo joinery. However with the passage of time and the improvement in tools, people started making various other small utility and decorative articles by cutting coconut shell or by carving coconut wood. 2. Regions of Production Coconut shell and wood craft is primarily prevalent in Kerala: in and around Calicut, Trivandrum, Attingal, Neyyatinkara and Quilandy in Kozhikode. Other states where this craft is practiced are Goa, the Andaman and Nicobar Islands and a few parts of Bengal, Pondicherry and Tamil Nadu. Another instance of availability of coconut shell craft is in the tribal belt of Bastar where intricately designed patterns in white metal are inlayed in the shell and cut to make bangles This craft is also prevalent in other countries such as Cambodia, Thailand, the Philippines, Java, Maldives and Sri Lanka. -
Annual Report 2018-19
18 ANNUAL REPORT 19 www.pidilite.com Floor th Jamnalal Bajaj Marg 208 Nariman Point Mumbai 400 021 DESIGN Pidilite Design Studio + Design Orb | PRINT Parksons Graphics Pidilite Industries Limited Office Registered Regent Chambers, 7 Please check spine before printing check spine before Please Sixty years is a good time to pause, look back and look ahead. In the last six decades, Fevicol has grown as a brand, touched lives in so many ways, and helped build bonds with our employees, dealers, distributors, carpenters, consumers and more. Tracing the journey of Fevicol gives us invaluable insights into how it became one of the most trusted and loved brands in India. These insights will continue to guide us as we travel further on this journey. M B Parekh Chairman ell, the Bond has lasted beyond the chair and now helps bond 1,60,000+ carpenters through the Fevicol Champions’ Club. ell, the Bond has lasted beyond the chair and now helps bond 1,60,000+ carpenters through the Fevicol Champions’ Club. PIDILITE ANNUAL REPORT 2018-19 3 years hence and with 29 Abbys and more, we are still counting. years hence and with 29 Abbys and more, we are still counting. PIDILITE ANNUAL REPORT 2018-19 5 evicol still stands tall as India’s most trusted brand in the adhesive category, and touches over 50 lakh households every year. Fevicol was ranked 38 in The Economic Times - Brand Equity’s survey of the 100 most trusted brands for the year 2018 and was 1st in the adhesive category. evicol still stands tall as India’s most trusted brand in the adhesive category, and touches over 50 lakh households every year. -

Business Ideas for Manufacturing of Adhesive (Fevicol Type). Profit
Y-1760 www.entrepreneurindia.co www.niir.org INTRODUCTION Adhesives are a broad term that refers to any substance that can be used to keep, fasten, or bind two or more materials or objects (i.e. substrates) together when placed between their surfaces. The adhesion (i.e., bond strength) created between substrates by the adhesive is largely determined by the adhesive's properties- specifically, its adhesion and cohesion. www.entrepreneurindia.co www.niir.org Due to the fact that these properties are the primary mechanisms underlying adhesives, measuring the failure point of both properties for each adhesive available aids in determining the best adhesive for use in a given application based on the technical requirements and specifications. www.entrepreneurindia.co www.niir.org Adhesives are commonly used in a number of residential, commercial, and industrial applications for permanent, semi- permanent, and temporary attachment purposes. Load carrying ability, chemical composition, reactivity or inertness, and shape are some of the characteristics that can be used to classify and categorise the wide variety of adhesives available. www.entrepreneurindia.co www.niir.org Each of these adhesives has unique properties and benefits, however, as with adhesive and cohesive strengths, the suitability of each property or feature (and the corresponding adhesive) is determined by the application. www.entrepreneurindia.co www.niir.org COMMON TYPES OF ADHESIVES Anaerobic Adhesives: Acrylic-based adhesives that cure in the absence of air are known as anaerobic adhesives. The curing process is accelerated when metal is present. This type of adhesive usually has a low viscosity, comes in liquid and paste forms, and is used to secure, seal, and preserve close-fitting and structural parts. -

Asia Pacific Leaders Sustainability Strategy Investment Rationales Q 31 March 2021 1 Investment Terms
Asia Pacific Leaders Sustainability Strategy Investment rationales Q 31 March 2021 1 Investment terms View our list of investment terms to help you understand the terminology within this document. 01 Advantech Founder owns approximately a third of the company Company profile: Advantech is a global leader in industrial computing. Industrial PCs are a small market compared to PCs or smartphones but they are a key element of the infrastructure in the Internet of Things (IoT) ecosystem which bridges across multiple applications and industries. What we like: Relevant Sustainable Development Goals: > Advantech’s strong brand name, broad product portfolio and Advantech have been at the forefront of moving leading market share mean they are likely to benefit from from ‘industrial specialised’ to ‘intelligent the structural growth in smart manufacturing and the IoT. specialised’. > This is underpinned by the rising number of connected devices and the expansion of big data which together Advantech is a highly desirable employer in drives efficiency gains across multiple industries and Taiwan, paying above average wages to around sectors. 10,000 employees and offering good prospects > The net cash balance sheet and strong free cash flow for career advancement. generation provide resilience and funds for future expansion. Risk: Areas for engagement: We believe that risks to the company include weak demand > Gender diversity. driven by a slower economy and increasing competition. > Supply chain due diligence. 02 Bank Central Asia Hartono family owns 59% Company profile: Bank Central Asia is one of the leading banks in Indonesia with a leading deposit base and strong track record of high quality lending. -

Annual Report 2004-05 1 Cyan Magenta Yellow Black Goodwin Multimedia Page-2
Cyan Magenta Yellow Black Goodwin Multimedia_Page-1 Contents Company Information .............................................. 2 Management Discussion and Analysis ....................... 3 Some Facts on Pidilite .............................................. 6 Financial Charts ........................................................ 7 10 Years Financial Performance ................................. 8 Economic Value Added (EVA) ................................. 10 Directors Report .................................................... 11 Auditors Report ...................................................... 18 Balance Sheet ........................................................ 20 Profit & Loss Account ............................................. 21 Schedules .............................................................. 22 Cash Flow Statement ............................................. 39 Statement Pursuant to Section 212 ......................... 41 Corporate Governance Report ................................ 42 Auditors Certificate on Corporate Governance ........ 45 Information for Shareholders .................................. 46 Consolidated Financial Statements .......................... 48 Pidilite Annual Report 2004-05 1 Cyan Magenta Yellow Black Goodwin Multimedia_Page-2 Company Information Board of Directors* B.K. Parekh Chairman S.K. Parekh Vice Chairman M.B. Parekh Managing Director N.K. Parekh Joint Managing Director H.K. Parekh Director R.M. Gandhi Director N.J. Jhaveri Director Bansi S. Mehta Director Ranjan Kapur