Determine the Partial Molal Volumes of Sodium Chloride and Water in a Series of Solutions from 0.3 to 3.0 M
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Thermodynamics Notes
Thermodynamics Notes Steven K. Krueger Department of Atmospheric Sciences, University of Utah August 2020 Contents 1 Introduction 1 1.1 What is thermodynamics? . .1 1.2 The atmosphere . .1 2 The Equation of State 1 2.1 State variables . .1 2.2 Charles' Law and absolute temperature . .2 2.3 Boyle's Law . .3 2.4 Equation of state of an ideal gas . .3 2.5 Mixtures of gases . .4 2.6 Ideal gas law: molecular viewpoint . .6 3 Conservation of Energy 8 3.1 Conservation of energy in mechanics . .8 3.2 Conservation of energy: A system of point masses . .8 3.3 Kinetic energy exchange in molecular collisions . .9 3.4 Working and Heating . .9 4 The Principles of Thermodynamics 11 4.1 Conservation of energy and the first law of thermodynamics . 11 4.1.1 Conservation of energy . 11 4.1.2 The first law of thermodynamics . 11 4.1.3 Work . 12 4.1.4 Energy transferred by heating . 13 4.2 Quantity of energy transferred by heating . 14 4.3 The first law of thermodynamics for an ideal gas . 15 4.4 Applications of the first law . 16 4.4.1 Isothermal process . 16 4.4.2 Isobaric process . 17 4.4.3 Isosteric process . 18 4.5 Adiabatic processes . 18 5 The Thermodynamics of Water Vapor and Moist Air 21 5.1 Thermal properties of water substance . 21 5.2 Equation of state of moist air . 21 5.3 Mixing ratio . 22 5.4 Moisture variables . 22 5.5 Changes of phase and latent heats . -

Molar Volume of a Gas
Science Enhanced Scope and Sequence – Chemistry Molar Volume of a Gas Strand Molar Relationships Topic Investigating molar volume of a gas Primary SOL CH.4 The student will investigate and understand that chemical quantities are based on molar relationships. Key concepts include a) Avogadro’s principle and molar volume; b) stoichiometric relationships. Related SOL CH.1 The student will investigate and understand that experiments in which variables are measured, analyzed, and evaluated produce observations and verifiable data. Key concepts include a) designated laboratory techniques; b) safe use of chemicals and equipment; f) mathematical and procedural error analysis; g) mathematical manipulations including SI units, scientific notation, linear equations, graphing, ratio and proportion, significant digits, and dimensional analysis. CH.2 The student will investigate and understand that the placement of elements on the periodic table is a function of their atomic structure. The periodic table is a tool used for the investigations of h) chemical and physical properties. CH.3 The student will investigate and understand how conservation of energy and matter is expressed in chemical formulas and balanced equations. Key concepts include b) balancing chemical equations. CH.5 The student will investigate and understand that the phases of matter are explained by kinetic theory and forces of attraction between particles. Key concepts include a) pressure, temperature, and volume; b) partial pressure and gas laws; c) vapor pressure. Background Information Avogadro’s law says that the volume of one mole of any gas at standard temperature and pressure is 22.4 liters. This is a necessary concept for the completion of stoichiometric problems that involve the use of gases as reactants or products. -
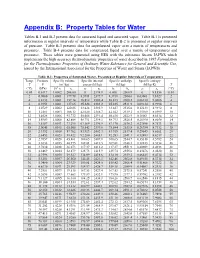
Appendix B: Property Tables for Water
Appendix B: Property Tables for Water Tables B-1 and B-2 present data for saturated liquid and saturated vapor. Table B-1 is presented information at regular intervals of temperature while Table B-2 is presented at regular intervals of pressure. Table B-3 presents data for superheated vapor over a matrix of temperatures and pressures. Table B-4 presents data for compressed liquid over a matrix of temperatures and pressures. These tables were generated using EES with the substance Steam_IAPWS which implements the high accuracy thermodynamic properties of water described in 1995 Formulation for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use, issued by the International Associated for the Properties of Water and Steam (IAPWS). Table B-1: Properties of Saturated Water, Presented at Regular Intervals of Temperature Temp. Pressure Specific volume Specific internal Specific enthalpy Specific entropy T P (m3/kg) energy (kJ/kg) (kJ/kg) (kJ/kg-K) T 3 (°C) (kPa) 10 vf vg uf ug hf hg sf sg (°C) 0.01 0.6117 1.0002 206.00 0 2374.9 0.000 2500.9 0 9.1556 0.01 2 0.7060 1.0001 179.78 8.3911 2377.7 8.3918 2504.6 0.03061 9.1027 2 4 0.8135 1.0001 157.14 16.812 2380.4 16.813 2508.2 0.06110 9.0506 4 6 0.9353 1.0001 137.65 25.224 2383.2 25.225 2511.9 0.09134 8.9994 6 8 1.0729 1.0002 120.85 33.626 2385.9 33.627 2515.6 0.12133 8.9492 8 10 1.2281 1.0003 106.32 42.020 2388.7 42.022 2519.2 0.15109 8.8999 10 12 1.4028 1.0006 93.732 50.408 2391.4 50.410 2522.9 0.18061 8.8514 12 14 1.5989 1.0008 82.804 58.791 2394.1 58.793 2526.5 -

Equation of State of an Ideal Gas
ASME231 Atmospheric Thermodynamics NC A&T State U Department of Physics Dr. Yuh-Lang Lin http://mesolab.org [email protected] Lecture 3: Equation of State of an Ideal Gas As mentioned earlier, the state of a system is the condition of the system (or part of the system) at an instant of time measured by its properties. Those properties are called state variables, such as T, p, and V. The equation which relates T, p, and V is called equation of state. Since they are related by the equation of state, only two of them are independent. Thus, all the other thermodynamic properties will depend on the state defined by two independent variables by state functions. PVT system: The simplest thermodynamic system consists of a fixed mass of a fluid uninfluenced by chemical reactions or external fields. Such a system can be described by the pressure, volume and temperature, which are related by an equation of state f (p, V, T) = 0, (2.1) 1 where only two of them are independent. From physical experiments, the equation of state for an ideal gas, which is defined as a hypothetical gas whose molecules occupy negligible space and have no interactions, may be written as p = RT, (2.2) or p = RT, (2.3) where -3 : density (=m/V) in kg m , 3 -1 : specific volume (=V/m=1/) in m kg . R: specific gas constant (R=R*/M), -1 -1 -1 -1 [R=287 J kg K for dry air (Rd), 461 J kg K for water vapor for water vapor (Rv)]. -

Research Article Densities, Apparent Molar Volume, Expansivities, Hepler's Constant, and Isobaric Thermal Expansion Coefficien
Hindawi International Journal of Chemical Engineering Volume 2018, Article ID 8689534, 10 pages https://doi.org/10.1155/2018/8689534 Research Article Densities, Apparent Molar Volume, Expansivities, Hepler’s Constant, and Isobaric Thermal Expansion Coefficients of the Binary Mixtures of Piperazine with Water, Methanol, and Acetone at T = 293.15 to 328.15 K Qazi Mohammed Omar ,1 Jean-Noe¨l Jaubert ,2 and Javeed A. Awan 1 1Institute of Chemical Engineering and Technology, Faculty of Engineering and Technology, University of the Punjab, Lahore, Pakistan 2Universit´e de Lorraine, Ecole Nationale Sup´erieure des Industries Chimiques, Laboratoire R´eactions et G´enie des Proc´ed´es (UMR CNRS 7274), 1 rue Grandville, 54000 Nancy, France Correspondence should be addressed to Jean-Noe¨l Jaubert; [email protected] and Javeed A. Awan; javeedawan@ yahoo.com Received 11 May 2018; Revised 26 July 2018; Accepted 2 September 2018; Published 14 November 2018 Academic Editor: Gianluca Di Profio Copyright © 2018 Qazi Mohammed Omar et al. 2is is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. 2e properties of 3 binary mixtures containing piperazine were investigated in this work. In a first step, the densities for the two binary mixtures (piperazine + methanol) and (piperazine + acetone) were measured in the temperature range of 293.15 to 328.15 K and 293.15 to 323.15 K, respectively, at atmospheric pressure by using a Rudolph research analytical density meter (DDM 2911). 2e concentration of piperazine in the (piperazine + methanol) mixture was varied from 0.6978 to 14.007 mol/kg, and the concentration of piperazine in the (piperazine + acetone) mixture was varied from 0.3478 to 1.8834 mol/kg. -

Solution Is a Homogeneous Mixture of Two Or More Substances in Same Or Different Physical Phases. the Substances Forming The
CLASS NOTES Class:12 Topic: Solutions Subject: Chemistry Solution is a homogeneous mixture of two or more substances in same or different physical phases. The substances forming the solution are called components of the solution. On the basis of number of components a solution of two components is called binary solution. Solute and Solvent In a binary solution, solvent is the component which is present in large quantity while the other component is known as solute. Classification of Solutions Solubility The maximum amount of a solute that can be dissolved in a given amount of solvent (generally 100 g) at a given temperature is termed as its solubility at that temperature. The solubility of a solute in a liquid depends upon the following factors: (i) Nature of the solute (ii) Nature of the solvent (iii) Temperature of the solution (iv) Pressure (in case of gases) Henry’s Law The most commonly used form of Henry’s law states “the partial pressure (P) of the gas in vapour phase is proportional to the mole fraction (x) of the gas in the solution” and is expressed as p = KH . x Greater the value of KH, higher the solubility of the gas. The value of KH decreases with increase in the temperature. Thus, aquatic species are more comfortable in cold water [more dissolved O2] rather than Warm water. Applications 1. In manufacture of soft drinks and soda water, CO2 is passed at high pressure to increase its solubility. 2. To minimise the painful effects (bends) accompanying the decompression of deep sea divers. O2 diluted with less soluble. -
![[5] Magnetic Densimetry: Partial Specific Volume and Other Applications](https://docslib.b-cdn.net/cover/6742/5-magnetic-densimetry-partial-specific-volume-and-other-applications-566742.webp)
[5] Magnetic Densimetry: Partial Specific Volume and Other Applications
74 MOLECULAR WEIGHT DETERMINATIONS [5] [5] Magnetic Densimetry: Partial Specific Volume and Other Applications By D. W. KUPKE and J. W. BEAMS This chapter consists of three parts. Part I is a summary of the principles and current development of the magnetic densimeter, with which density values may be obtained conveniently on small volumes of solution with the speed and accuracy required for present-day ap- plications in protein chemistry. In Part II, the applications, including definitions, are outlined whereby the density property may be utilized for the study of protein solutions. Finally, in Part III, some practical aspects on the routine determination of densities of protein solutions by magnetic densimetry are listed. Part I. Magnetic Densimeter The magnetic densimeter measures by electromagnetic methods the vertical (up or down) force on a totally immersed buoy. From these measured forces together with the known mass and volume of the buoy, the density of the solution can be obtained by employing Archimedes' principle. In practice, it is convenient to eliminate evaluation of the mass and volume of the buoy and to determine the relation of the mag- netic to the mechanical forces on the buoy by direct calibration of the latter when it is immersed in liquids of known density. Several workers have devised magnetic float methods for determin- ing densities, but the method first described by Lamb and Lee I and later improved by MacInnes, Dayhoff, and Ray: is perhaps the most accurate means (~1 part in 106) devised up to that time for determining the densities of solutions. The magnetic method was not widely used, first because it was tedious and required considerable manipulative skill; second, the buoy or float was never stationary for periods long enough to allow ruling out of wall effects, viscosity perturbations, etc.; third, the technique required comparatively large volumes of the solution (350 ml) for accurate measurements. -

Chapter 3 3.4-2 the Compressibility Factor Equation of State
Chapter 3 3.4-2 The Compressibility Factor Equation of State The dimensionless compressibility factor, Z, for a gaseous species is defined as the ratio pv Z = (3.4-1) RT If the gas behaves ideally Z = 1. The extent to which Z differs from 1 is a measure of the extent to which the gas is behaving nonideally. The compressibility can be determined from experimental data where Z is plotted versus a dimensionless reduced pressure pR and reduced temperature TR, defined as pR = p/pc and TR = T/Tc In these expressions, pc and Tc denote the critical pressure and temperature, respectively. A generalized compressibility chart of the form Z = f(pR, TR) is shown in Figure 3.4-1 for 10 different gases. The solid lines represent the best curves fitted to the data. Figure 3.4-1 Generalized compressibility chart for various gases10. It can be seen from Figure 3.4-1 that the value of Z tends to unity for all temperatures as pressure approach zero and Z also approaches unity for all pressure at very high temperature. If the p, v, and T data are available in table format or computer software then you should not use the generalized compressibility chart to evaluate p, v, and T since using Z is just another approximation to the real data. 10 Moran, M. J. and Shapiro H. N., Fundamentals of Engineering Thermodynamics, Wiley, 2008, pg. 112 3-19 Example 3.4-2 ---------------------------------------------------------------------------------- A closed, rigid tank filled with water vapor, initially at 20 MPa, 520oC, is cooled until its temperature reaches 400oC. -

The Molar Volume of a Gas
THE MOLAR VOLUME OF A GAS OBJECTIVE: To calculate the standard molar volume of a gas from accumulated data INTRODUCTION Solids, liquids and gases are called the three states of matter. In this experiment, we will examine the gaseous state. The "condition" or state of a gaseous substance is determined by four properties: volume (V), pressure (P), temperature (T), and the number of moles of the substance present (n). A change in one variable causes a change in one or more of the other variables. If any 3 of the variables are known, the fourth can be calculated using the ideal gas law: PV = nRT (1) where R is a constant determined from experiment. It is called the universal gas constant. One mole of any gas at 0.00EC (273 K) and 1.00 atm (760 torr) occupies a volume of 22.4 L. These conditions are called standard temperature and pressure, or STP, and 22.4 L is called the standard molar volume. Using this data, R can be calculated: R = PV = (1.00 atm)(22.4 L) = 0.0821 L@atm (2) nT (1.00 mol) (273 K) mol@K If the number of moles of gas is constant, another useful relationship is the combined gas law: P1V1 = P2V2 (3) T1 T2 If P, V and T are known under an initial set of conditions and 2 of the conditions change, the change in the third can be calculated. For example, if a sample of 0.0500 moles of a gas occupies a 1.42 L container at 298 K and 654 torr, the volume it will occupy at 323 K and 985 torr is: (654 torr)(1.42 L) = (985 torr)(V2) (4) 298 K 323 K V2 = (654 torr)(1.42 L)(323 K) = 1.02 (5) (985 torr)(298 K) The volume occupied by 1 mole of gas under these nonstandard conditions would be: (1.02 L) = 20.4 L/mol (6) (0.050 mol) Note: Pressure units do not have to be changed to atm, as long as the units cancel out. -

Ideal Gasses Is Known As the Ideal Gas Law
ESCI 341 – Atmospheric Thermodynamics Lesson 4 –Ideal Gases References: An Introduction to Atmospheric Thermodynamics, Tsonis Introduction to Theoretical Meteorology, Hess Physical Chemistry (4th edition), Levine Thermodynamics and an Introduction to Thermostatistics, Callen IDEAL GASES An ideal gas is a gas with the following properties: There are no intermolecular forces, except during collisions. All collisions are elastic. The individual gas molecules have no volume (they behave like point masses). The equation of state for ideal gasses is known as the ideal gas law. The ideal gas law was discovered empirically, but can also be derived theoretically. The form we are most familiar with, pV nRT . Ideal Gas Law (1) R has a value of 8.3145 J-mol1-K1, and n is the number of moles (not molecules). A true ideal gas would be monatomic, meaning each molecule is comprised of a single atom. Real gasses in the atmosphere, such as O2 and N2, are diatomic, and some gasses such as CO2 and O3 are triatomic. Real atmospheric gasses have rotational and vibrational kinetic energy, in addition to translational kinetic energy. Even though the gasses that make up the atmosphere aren’t monatomic, they still closely obey the ideal gas law at the pressures and temperatures encountered in the atmosphere, so we can still use the ideal gas law. FORM OF IDEAL GAS LAW MOST USED BY METEOROLOGISTS In meteorology we use a modified form of the ideal gas law. We first divide (1) by volume to get n p RT . V we then multiply the RHS top and bottom by the molecular weight of the gas, M, to get Mn R p T . -

Physical Chemistry
Subject Chemistry Paper No and Title 10, Physical Chemistry- III (Classical Thermodynamics, Non-Equilibrium Thermodynamics, Surface chemistry, Fast kinetics) Module No and Title 10, Free energy functions and Partial molar properties Module Tag CHE_P10_M10 CHEMISTRY Paper No. 10: Physical Chemistry- III (Classical Thermodynamics, Non-Equilibrium Thermodynamics, Surface chemistry, Fast kinetics) Module No. 10: Free energy functions and Partial molar properties TABLE OF CONTENTS 1. Learning outcomes 2. Introduction 3. Free energy functions 4. The effect of temperature and pressure on free energy 5. Maxwell’s Relations 6. Gibbs-Helmholtz equation 7. Partial molar properties 7.1 Partial molar volume 7.2 Partial molar Gibb’s free energy 8. Question 9. Summary CHEMISTRY Paper No. 10: Physical Chemistry- III (Classical Thermodynamics, Non-Equilibrium Thermodynamics, Surface chemistry, Fast kinetics) Module No. 10: Free energy functions and Partial molar properties 1. Learning outcomes After studying this module you shall be able to: Know about free energy functions i.e. Gibb’s free energy and work function Know the dependence of Gibbs free energy on temperature and pressure Learn about Gibb’s Helmholtz equation Learn different Maxwell relations Derive Gibb’s Duhem equation Determine partial molar volume through intercept method 2. Introduction Thermodynamics is used to determine the feasibility of the reaction, that is , whether the process is spontaneous or not. It is used to predict the direction in which the process will be spontaneous. Sign of internal energy alone cannot determine the spontaneity of a reaction. The concept of entropy was introduced in second law of thermodynamics. Whenever a process occurs spontaneously, then it is considered as an irreversible process. -

TABLE A-2 Properties of Saturated Water (Liquid–Vapor): Temperature Table Specific Volume Internal Energy Enthalpy Entropy # M3/Kg Kj/Kg Kj/Kg Kj/Kg K Sat
720 Tables in SI Units TABLE A-2 Properties of Saturated Water (Liquid–Vapor): Temperature Table Specific Volume Internal Energy Enthalpy Entropy # m3/kg kJ/kg kJ/kg kJ/kg K Sat. Sat. Sat. Sat. Sat. Sat. Sat. Sat. Temp. Press. Liquid Vapor Liquid Vapor Liquid Evap. Vapor Liquid Vapor Temp. Њ v ϫ 3 v Њ C bar f 10 g uf ug hf hfg hg sf sg C O 2 .01 0.00611 1.0002 206.136 0.00 2375.3 0.01 2501.3 2501.4 0.0000 9.1562 .01 H 4 0.00813 1.0001 157.232 16.77 2380.9 16.78 2491.9 2508.7 0.0610 9.0514 4 5 0.00872 1.0001 147.120 20.97 2382.3 20.98 2489.6 2510.6 0.0761 9.0257 5 6 0.00935 1.0001 137.734 25.19 2383.6 25.20 2487.2 2512.4 0.0912 9.0003 6 8 0.01072 1.0002 120.917 33.59 2386.4 33.60 2482.5 2516.1 0.1212 8.9501 8 10 0.01228 1.0004 106.379 42.00 2389.2 42.01 2477.7 2519.8 0.1510 8.9008 10 11 0.01312 1.0004 99.857 46.20 2390.5 46.20 2475.4 2521.6 0.1658 8.8765 11 12 0.01402 1.0005 93.784 50.41 2391.9 50.41 2473.0 2523.4 0.1806 8.8524 12 13 0.01497 1.0007 88.124 54.60 2393.3 54.60 2470.7 2525.3 0.1953 8.8285 13 14 0.01598 1.0008 82.848 58.79 2394.7 58.80 2468.3 2527.1 0.2099 8.8048 14 15 0.01705 1.0009 77.926 62.99 2396.1 62.99 2465.9 2528.9 0.2245 8.7814 15 16 0.01818 1.0011 73.333 67.18 2397.4 67.19 2463.6 2530.8 0.2390 8.7582 16 17 0.01938 1.0012 69.044 71.38 2398.8 71.38 2461.2 2532.6 0.2535 8.7351 17 18 0.02064 1.0014 65.038 75.57 2400.2 75.58 2458.8 2534.4 0.2679 8.7123 18 19 0.02198 1.0016 61.293 79.76 2401.6 79.77 2456.5 2536.2 0.2823 8.6897 19 20 0.02339 1.0018 57.791 83.95 2402.9 83.96 2454.1 2538.1 0.2966 8.6672 20 21 0.02487 1.0020