DOCSLIB.ORG

Cross-Sections of 14 Mev Neutron Induced Reactions on Some Isotopes of Chromium, Zirconium and Tin

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Cross-Sections of 14 Mev Neutron Induced Reactions on Some Isotopes of Chromium, Zirconium and Tin Indian Journal of Pure & Applied Physics Vol. 44, March 2006, pp. 216-219 Cross-sections of 14 MeV neutron induced reactions on some isotopes of chromium, zirconium and tin Sneh Lata Goyal* & R K Mohindra *Department of Applied Physics, Guru Jambheshwar University, Hisar 125 001 Department of Physics, Kurukshetra University, Kurukshetra 132 119 Received 30 May 2005; revised 23 November 2005; accepted 6 January 2006 Neutron induced reaction cross-sections of the isotopes 52Cr, 53Cr, 90Zr, 91Zr, 92Zr, 94Zr, 116Sn, 118Sn and 120Sn for (n,p), (n,n’), (n,α) and (n, 2n) reactions have been evaluated at 14 MeV. The computations are based on the evaporation model considering the pre-equilibrium emission mechanism under some approximations. The computer codes ALICE-91, NX-1 and SC2N3N have been used. These cross-sections were also computed using the level density formula of Lang and Le Couteur with and without applying pairing energy correction. The compound nucleus theory based on Fermi gas and evaporation model with optical model potential parameters has been used. The neutron, proton and alpha penetrabilities and inverse reaction cross-sections have been computed using the computer code SCAT-2. The computed cross-sections have been compared with the available experimental values and the results are in fairly good agreement. Keywords: Neutron induced reactions, Nuclear physics, Neutron energy, Neutron multiplication, Nuclear heating, Nuclear transmutation, Radiation damage IPC Code: G01T3/00 1 Introduction the computation of (n,p), (n,n’), (n,α) and (n, 2n) Activation cross-sections for production of long- reaction cross-sections induced by 14 MeV neutrons. lived isotopes at around 14 MeV neutron energy are The computations of (n,p), (n, α) and (n, 2n) reaction of interest for testing nuclear reaction models. cross-sections have been carried out using the Furthermore, in the case of structural materials of a computer codes ALICE-91 given by Blann4-6, NX-1 fusion reactor, the data are important for the given by Zhao Zhixiang and Zhou Delin7,8 and estimation of neutron multiplication, nuclear heating, SC2N3N developed by Zhang Zin et al.9,10. These nuclear transmutation and radiation damage effects. codes are based on the pre-equilibrium emission Zircalloy-2 (composition1 – Zr = 98.2%, Sn = 1.5%, mechanism. Also, the statistical model of nuclear Cr = 0.1%, Fe = 0.15%, Ni = 0.05%) is used as reactions has been extended for the computation of 1,2 cladding material in Pressurized Water Reactors such cross-sections. The compound nucleus theory (PWR), Pressurized Heavy Water Reactors (PHWR) based on Fermi gas and evaporation model with and Boiling Water Reactors (BWR). In PWR, the core optical model potential parameters has been used. The of the plate type seed elements is zirconium– uranium Lang and Le Couteur level density formula11,12 has alloy clad with zirconium alloy (zircalloy–2). been used for these computations. Zirconium was selected because of its small absorption cross-section. In BWR, the core contains 2 Calculations 15.4% of zircalloy -2 by volume percentage. The computer code ALICE-91 (Refs 4-6) has been 3 Various nuclear reaction models are currently used for the computation of (n,p), (n,α) and (n, 2n) being applied to evaluate the neutron induced reaction reaction cross-sections induced by 14 MeV neutrons cross-sections. The success of optical model in of the isotopes 52Cr, 53Cr, 90Zr, 91Zr, 92Zr, 94Zr, 116Sn, explaining large number of features in elastic and 118Sn and 120Sn. This code is based on the hybrid and inelastic scattering of nucleons with nuclei has created geometry dependent hybrid (GDH) model for the pre- a need for the computation of neutron cross-sections; equilibrium process and the Weisskopf–Ewing obtained from a detailed optical model potential with evaporation model for the equilibrium process. These real and imaginary parts. The present work deals with cross-sections were also computed after applying GOYAL & MOHINDRA: CROSS-SECTIONS OF 14 MeV NEUTRON INDUCED REACTIONS ON SOME ISOTOPES 217 pairing energy correction and shell correction with Table 1 ⎯ Optical model parameters for neutrons by Wilmore 13 backshifted pairing6 simultaneously. The Fermi gas and Hodgson Parameter Neutrons level density used is of the form: Real Potential Vr(MeV) 48 (Woods-Saxon) Imaginary W (MeV) 9.0 -5/4 s ρ (U) ∝ (U-δ) exp2 a(U − δ) …(1) Spin Orbit Vso (MeV) 7.0 -4 -6 2 Radius Rv(fm) =(1.322-7.6x10 A+ 4x10 A The level density parameter a = A/9 and the pairing – 8x10-9A3)xA1/3 -4 -6 2 correction is defined by δ = 11/A1/2, where A is mass Rw(fm) =(1.266-3.7x10 A+ 2x10 A – 4x10-9A3)xA1/3 number of the residual nucleus. Rso(fm) =Rw 1/3 The optical model potential is defined as follows: Rcoulomb =1.25 A Diffusivity 2 a′ (f ) 0.66 ⎛ h ⎞ v v m U(r) = V − V f (r) − i − iota[−4W g(r) + W f (r)] + ⎜ ⎟ (1.sr)v50h(r) c r s v ⎜ ⎟ a′w(fm) 0.48 ⎝ mπc ⎠ a′so(fm) 0.48 …(2) The binding energies and Q-values used in the present where work were all based on experimental masses. The ALICE code includes experimental masses in block 2 ⎧ zz' e / r, data, so that a simple input parameter results in all Q- ⎪ 2 2 ifr ≥ R c Vc = ⎨zz' e ⎛ r ⎞, … (3) values and binding energies being internally ⎜3 − ⎟ ifr〈R ⎪ 2R ⎜ R 2 ⎟ c generated from experimental mass tables. ⎩ c ⎝ c ⎠ In another computation, the cross-sections for (n,p) and (n, α) reactions at 14 MeV neutron energy have where z and z’ are the charges of the incident particle been computed using the computer code NX-1 given and the target nucleus. The imaginary absorptive by Zhao Zhixiang and Zhou Delin7,8 and (n, 2n) potential is pure surface so Ws ≠ 0 and Wv = 0, which reaction cross-sections have been computed using the have a derivative Woods-Saxon shape and computer code SC2N3N given by Zhang Zin et al.9,10. These codes contain analytical formulae with f(r) = [1 + exp(r − R)/a′ ]−1 …(4) v parameters based on experimental data and derived by using a constant temperature evaporation model for ′ ′ −2 …(5) g(r) = exp[(r − R)/a w ][1 + exp(r − R)/a w ] statistical phenomena and the exciton model for the and pre-compound part. 1d The detailed formulae for the computation of these h(r) = f(r) …(6) rdr cross-sections have been described by Bansal and Mohindra14. Here the pre-equilibrium emission is are the Woods-Saxon, derivative Woods-Saxon considered to occur only at the state of exciton (surface peaked) and spin-orbit form factors with number n = 3. The energy level density of the appropriate radius and diffusivity parameters. R = compound nucleus is taken in the form of constant 1/3 r0A is the nuclear radius and a′ is the surface temperature. diffuseness parameter. ρ (A, E) ∝ exp [E/T(A)] … (8) 2 ⎛ h ⎞ 2 ⎜ ⎟ = 2.0()fermi where E is excitation energy of the compound nucleus ⎜ m c ⎟ ⎝ π ⎠ and the nuclear temperature T(A) is taken as T(A) = and 13A-1/2. For these computations, the Q-values and r separation energies have been taken from the 1.sr = j()()()i + 1 −11 + 1 − s s +1 /2 … (7) tabulation of Audi et al.15. The computations of (n,p), (n,n’), (n, α) and (n, 2n) where s is spin angular momentum, l is orbital angular reaction cross-sections at 14 MeV have also been momentum and j is total angular momentum. carried out using the compound nucleus theory based For neutrons, the optical model parameter set due on the Fermi gas and evaporation model. The level to Wilmore and Hodgson13 listed in Table 1 is used. density formula of Lang and Le Couteur11,12 with and 218 INDIAN J PURE & APPL PHYS, VOL 44, MARCH 2006 without applying pairing energy correction16 has been Table 2 ⎯ Optical model parameters for neutrons by Becchetti 20 used. The neutron and proton penetrabilities listed by and Greenless 17 Mani et al . and alpha induced inverse reaction cross- Parameter Neutrons 18 sections given by Huizenga and Igo have been used. Real Potential Vr (MeV) 56.3 – 0.32E – 24 (N-Z)/A The neutron, proton and alpha penetrabilities and Imaginary Ws (MeV) 13-0.25E -12 (N-Z)/A or zero, whichever inverse reaction cross-sections have been computed is greater using the computer code SCAT-2 developed by Wv (MeV) 0.22E – 1.56 or zero, whichever is greater Bersillon19. The optical model potential parameter set Spin Orbit Vso (MeV) 6.2 20 1/3 for neutrons given by Becchetti and Greenless listed Radius Rv(fm) 1.17 A 1/3 in Table 2 is used. These computed values of inverse Rw(fm) 1.26 A 1/3 reaction cross-sections have also been used for the Rso(fm) 1.01 A Diffusivity computation of (n,p), (n,n’) and (n, α) reaction cross- a′v (fm) 0.75 sections at 14 MeV neutron energy using Lang and Le a′w (fm) 0.58 Couteur level density formula with and without the a′so (fm) 0.75 Table 3⎯ Computed reaction cross-sections at 14 MeV Isotope Reaction Computed Cross-sections (mbs) using Experimental Pre-equilibrium Emission Lang & Le Couteur Level Density Formula With Cross-sections Computed Inverse Cross-sections of (mbs) NX- 1/ ALICE-91 SCAT-2 Earlier Codes SC2N3N Without With Pairing With Shell Without With Pairing Without With Pairing Code Correction Energy Correction Correction Energy Correction Energy (n, n’) - - - - 1412.7 1307.5 1266.7 1127.9 1304 52Cr (n, 2n) 252.1 423.0 63.9 0.0 - - 126.1 - 278±20 (n, p) 77.3 40.2 32.0 66.8 25.3 129.9 33.8 171.9 78±10 (n, α) 32.2 4.7 3.5 14.1 10.4 12.8 14.6 17.6 35±3 (n, n’) - - - - 1405.5 1427.4 1251.2 1282.0 1366 53Cr (n, 2n) 895.2 1020.0 1020.0 600.0 - - - - 700 (n, p) 46.2 28.7 28.9 49.9 18.4 16.6 27.2 24.0 45±6 (n, α) 26.0 16.5 17.0 9.4 26.2 5.9 31.1 9.0 45±4 (n, n’) - - - - 1823.4 1806.9 1640.2
Load more

Recommended publications
  • Unit 1Moles and Equations
    Cambridge University Press 978-1-107-61665-3 – Cambridge International AS and A Level Chemistry Judith Potter Peter Cann Excerpt More information Moles and equations Unit 1 Learning outcomes You should be able to: defi ne and use the terms empirical and molecular formulae and use experimental data defi ne and use relative masses based on the to fi nd them, 12C scale write and construct equations and use them in defi ne and use the mole and Avogadro’s performing mole calculations constant perform mole calculations involving solutions analyse simple mass spectra and use the data in and gases, relative atomic mass calculations This unit gathers together the basic chemistry relative isotopic mass = calculations. You may need to refer to it as you revise mass of one atom of the isotope other topics in later units. (1/12) of the mass of one atom of 12C Relative masses are a ratio of two masses and have 1.01 Relative masses no units. An atom is the smallest part of an element that can exist and still retain the identity of the element. A 1.02 The mole and the molecule is a group of atoms bonded together and the smallest portion of an element or compound that can Avogadro constant exist alone. A simple ion is an atom which has lost or To give an easy measurement of mass, a number of gained one or more electrons. Atoms, molecules and atoms is chosen so that their combined mass is equal to ions are so small that their masses are far too small the relative atomic mass in grams.
    [Show full text]
  • Chromium Isotopes Detection in Their Ores with Minimal Errors
    Open Access Annals of Advances in Chemistry Research Article Chromium Isotopes Detection in their Ores with Minimal Errors ISSN 2576-3768 Loai Aljerf1* and Nuha AlMasri2 1Department of Basic Sciences, Faculty of Dental Medicine, Damascus University, Mazzeh Highway, Almazzeh, Damascus, Syria 2Department of Chemistry, Faculty of Medicine, Syrian Private University, Damascus, Syria *Address for Correspondence: Loai Aljerf, De- Abstract partment of Basic Sciences, Faculty of Dental Medicine, Damascus University, Mazzeh High- The industrial production and use of chromium have grown considerably during the past way, Almazzeh, Damascus, Syria, Tel: +963-93 fi ve decades. Abundances of the chromium isotopes in terrestrial samples are identical to 34 46 993; Email: [email protected]; 0.01%. Among the dominant species of chromium, the trivalent form widely occurs in nature in [email protected] chromite ores which is extremely immobilized especially in water bodies. Samples were mixtures Submitted: 21 July 2018 of separated chromium isotopes and the calibration was made with the same species as those Approved: 03 September 2018 used in the measurements. The method had simplifi ed the conversion of the ores to chromyl Published: 04 September 2018 fl uoride since the element could be readily separated as lead chromate from the leaching of Copyright: 2018 Aljerf L, et al. This is an open chromite-sodium peroxide fusions. Isotope assay of chromyl fl uoride under certain conditions access article distributed under the Creative was measured and the measurements of chromium isotopic anomalies ratios and isotope Commons Attribution License, which permits abundance of the chromite ores have been assessed. These provided suffi cient quantitative mass unrestricted use, distribution, and reproduction spectrometric data, which were analyzed to calculate the abundance and the mean atomic mass in any medium, provided the original work is of the questioned isotopes.
    [Show full text]
  • Determination of Picogram Quantities of Vanadium in Calcite And
    + + Anal. Chem. 1996, 68, 371-377 Determination of Picogram Quantities of Vanadium in Calcite and Seawater by Isotope Dilution Inductively Coupled Plasma Mass Spectrometry with Electrothermal Vaporization David W. Hastings* and Steven R. Emerson School of Oceanography, WB-10, University of Washington, Seattle, Washington 98195 Bruce K. Nelson Department of Geological Sciences, AJ-20, University of Washington, Seattle, Washington 98195 We developed a method to measure picogram quantities Recent interest in the geochemistry of vanadium has arisen of vanadium in calcite and seawater by isotope dilution from its unique redox behavior 9,10 and the observation of enriched (ID) inductively coupled plasma mass spectrometry using concentrations in anoxic sediments, black shale, and crude oil.11,12 electrothermal vaporization (ETV) to introduce the sample Because V deposition is redox sensitive, its concentration in into the plasma. A 50V isotope spike enriched to 44 atom seawater is most likely sensitive to the oxidation state of sedi- % was equilibrated with samples, followed by chemical ments. The calcitic shells of foraminifera accurately record purification by cation exchange chromatography. Samples seawater concentrations of V,13 so the V content of the fossil shells were introduced into the ETV unit with a Pd modifier and of these microscopic oceanic organisms potentially can serve as heated to 1000 °C. This quantitatively eliminates the an indicator of changes in past ocean anoxia.14 ClO+ isobaric interference with V at m/z 51 for solutions A typical 5 mg hand-picked sample of these microscopic shells up to 0.5 N HCl. The procedural blank was 0.27 pg of yields only 50-200 pg of vanadium.
    [Show full text]
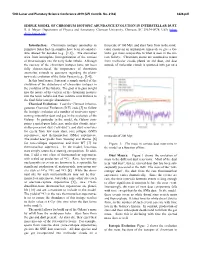
  • Simple Model of Chromium Isotopic Abundance Evolution in Interstellar Dust
    50th Lunar and Planetary Science Conference 2019 (LPI Contrib. No. 2132) 3226.pdf SIMPLE MODEL OF CHROMIUM ISOTOPIC ABUNDANCE EVOLUTION IN INTERSTELLAR DUST. B. S. Meyer,. Department of Physics and Astronomy, Clemson University, Clemson, SC 29634-0978, USA (mbra- [email protected]). Introduction: Chromium isotopic anomalies in timescale of 100 Myr, and stars form from in the mole- primitive Solar System samples have been of consider- cular clouds on an appropriate timescale to give a Ga- able interest for decades (e.g., [1,2]). The anomalies lactic gas mass comparable to what is seen in the cur- arise from incomplete homogenization of the carriers rent Galaxy. Chromium atoms are assumed to return of these isotopes into the early Solar nebula. Although from molecular clouds plated on old dust, and dust the carriers of the chromium isotopes have not been outside of molecular clouds is sputtered into gas on a fully characterized, the importance of chromium anomalies extends to questions regarding the plane- tary-scale evolution of the Solar System (e.g., [3,4]). In this brief paper, I present a simple model of the evolution of the abundances of chromium isotopes in the evolution of the Galaxy. The goal is to gain insight into the nature of the carriers of the chromium isotopes into the Solar nebula and their relative contributions to the final Solar isotopic abundances. Chemical Evolution: I use the Clemson Inhomo- geneous Chemical Evolution (ICE) code [5] to follow the isotopic evolution of a number of reservoirs repre- senting interstellar dust and gas in the evolution of the Galaxy.
    [Show full text]
  • Chromium Isotope Behaviour in Natural Waters
    UNIVERSITY OF SOUTHAMPTON FACULTY OF NATURAL AND ENVIRONMENTAL SCIENCES Ocean and Earth Sciences Chromium Isotope Behaviour in Natural Waters by Heather Jane Goring-Harford Thesis for the degree of Doctor of Philosophy June 2017 UNIVERSITY OF SOUTHAMPTON ABSTRACT FACULTY OF NATURAL AND ENVIRONMENTAL SCIENCES Ocean and Earth Sciences Doctor of Philosophy CHROMIUM ISOTOPE BEHAVIOUR IN NATURAL WATERS By Heather Jane Goring-Harford The isotopes of chromium (Cr) fractionate during terrestrial oxidation reactions that require the presence of oxygen. The main source of Cr to the oceans is via rivers, and thus Cr isotopic signatures (expressed as δ53Cr) preserved in authigenic sediments are increasingly being used to reconstruct the oxygen levels of ancient environments. However, Cr can undergo various reactions in natural waters that may fractionate Cr isotopes. The contribution of these reactions to authigenic sediment δ53Cr values is not well understood, and this limits the interpretation of δ53Cr values measured in ancient archives. This thesis describes the development of a method to accurately and precisely measure Cr isotopic signatures in natural waters with extremely low Cr concentrations, and evaluates the behaviour of Cr isotopes in water samples from a range of environmental settings. Seawater samples from the Atlantic Ocean Oxygen Minimum Zone (OMZ) were analysed to evaluate whether Cr isotopic fractionation was enhanced under depleted oxygen conditions. Results indicate that the Atlantic OMZ is not sufficiently depleted in oxygen to reduce and remove Cr from seawater, although δ53Cr values (1.08 – 1.72‰) were variable due to adsorption of Cr(III) to particles on the shelf, and hydrological mixing. Black Sea seawater samples that had dissolved oxygen concentrations close to zero were enriched in 52Cr, resulting in a δ53Cr that was 0.38‰ lower than the overlying fully oxygenated waters.
    [Show full text]
  • ILPAC Unit S2: Atomic Structure
    UNIT INDEPENDENT LEARNING PROJECT FOR ADVANCED CHEMISTRY Periodic Table of the Elements o 2 I He II ill] III IV V VI VIII 4.0 3 4 5 6 7 8 9 10 Li Be B C N 0 F Ne 6.9 9.0 10.8 12.0 14.0 16.0 19.0 20.2 11 12 13 14 15 16 17 18 Na Mg Al Si P S CI Ar 23.0 24.3 27.0 28.1 31.0 32.1 35.5 39.9 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 3! 36 K Ca Sc Ti V Cr Mn Fe Co Ni eu Zn Ga Ge As Se BrlKr 39.1 40.1 45.0 47.9 50.9 52.0 54.9 55.9 58.9 58.7 63.5 65.4 69.7 72.6 74.9 79.0 79 83.8 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 S4 Rb Sr Y Zr Nb Mo Tc Ru Rh Pd Ag Cd In Sn Sb Te I Xe 85.5 87.6 88.9 91.2 92.9 95.9 99.0 101.1 102.9 106.4 107.9 112.4 114.8 118.7 121.8 127.6 126.91 ' 3 ' . 3 55 56 57 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 Cs Ba La 4 Hf Ta W Re Os If Pt Au Hg Tl Pb Bi Po AtlRn 132.9 137.3 138.9 178.5 181.0 183.9 186.2 190.2 192.2 195.1 197.0 200.6 204.4 207.2 209.0 210.0 210.01222.0 87 88 89 Fr Ra Ac~ 223.0 226.0 227.0 58 59 60 61 62 63 64 65 66 67 68 69 70 71 Ce Pr Nd Pm Sm Eu Gd Tb Dy Ho Er Tm Yb Lu 140.1 140.9 144.2 (147) 150.4 152.0 157.3 158.9 162.5 164.9 167.3 168.9 173.0 175.0 90 91 92 93 94 95 96 97 98 99 100 101 102 103 "--- Th Pa U Np Pu Am Cm Bk Cf Es Fm Md No Lw 232.0 231.0 238.1 (237) 239.1 (243) (241) (247) (251 ) (254) (253) (256) ( 254) (257) A value in brackets denotes the mass number of the most stable isotope.
    [Show full text]
  • 45024017.Pdf
    Ain Shams University Faculty of Science Radiochemical Study on the Separation of Chromium-51 from the Irradiated Target by Using Commercial and/or Synthesized Ion Exchanger A thesis Submitted by Mohamed Ismail Mohamed Mohamed Aydia (M. Sc. Inorganic and Physical Chemistry 2007) Chemist\ Radioisotopes Production Facility Egyptian Second Research Reactor Atomic Energy Authority For the Degree of Doctor of Philosophy in Science (Chemistry). Department of Chemistry Faculty of Science Ain Shams University (2012) Ain Shams University Faculty of Science Approval Sheet The Thesis entitled Radiochemical Study on the Separation of Chromium-51 from the Irradiated Target by Using Commercial and/or Synthesized Ion Exchanger Submitted by/ Mohamed Ismail Mohamed Aydia (M. Sc. Inorganic and Physical Chemistry 2007) For the Degree of Doctor of Philosophy in Science (Chemistry). This thesis has been approved by supervisor committee SUPERVISORS • Prof. Dr. M.S. Abdel-Mottaleb ….……………… Professor of Inorganic Chemistry Faculty of Science-Ain Shams University • Prof. Dr. Salah Soliman ….……………… Ex-Chairman of Hot Labs Center Supervisor of Radioisotopes Production Facility Atomic Energy Authority • Prof. Dr. A. A. El-Mohty ….……………… Professor of Radiochemistry Radioactive Isotopes and Generator Dep. Atomic Energy Authority • Prof. K.M. El-Azony ….……………… Associate Professor of Radiochemistry Radioactive Isotopes and Generator Dep. Atomic Energy Authority. Prof. Dr. Maged Shafik Antonious Head of Chemistry Department Faculty of Science - Ain Shams University CHAPTER (I) INTRODUCTION CHAPTER (II) EXPERIMENTAL CHAPTER (III) RESULTS AND DISCUSSION REFERENCES ] SUMMARY ARABIC SUMMARY ACKNOWLEDGEMENT I would like to express my gratitude to Prof. Dr. Mohamed Sabry Abdel-Mottaleb, Professor of Inorganic Chemistry, Faculty of Science, Ain Shams University for his supervision and his sponsorship for this work.
    [Show full text]
  • The Radiochemistry of Chromium COMMITTEE on NUCLEAR SCIENCE
    546.7 P634v C95 National Academy of Sciences 1 National Research Council B I I NUCLEAR SCIENCE SERIES I 1 I I The Radiochemistry of Chromium COMMITTEE ON NUCLEAR SCIENCE L. F. CURTISS, Chairman ROBLEY D. EVANS, Vice Chairman NationalBureau ofStandards MassachusettsInstituteofTechnology J.A, DeJUREN, Secretary WestinghouseElectricCorporation H, J.CURTIS G. G. MANOV BrookhavenNationalLaboratory Tracerlab,Inc. SAMUEL EPSTEIN W. WAYNE MEINKE CaliforniaInstituteofTechnology UniversityofMichigan HERBERT GOLDSTEIN A. H. SNELL NuclearDevelopmentCorporationof Oak RidgeNationalLaboratory America E. A. UEHLING H. J.GOMBERG UniversityofWashington UniversityofMichigan D. M. VAN PATTER E. D. KLEMA BartolResearch Foundation NorthwesternUniversity ROBERT L. PLATZMAN Argonne NationalLaboratory LIAISON MEMBERS PAUL C .AEBERSOLD W. D. URRY Atomic Energy Commission U. S.Air Force J. HOWARD McMILLEN WILLIAM E. WRIGHT NationalScienceFoundation OfficeofNavalResearch SUBCOMMITTEE ON RADIOCHEMISTRY W. WAYNE MEINKE, Chairman EARL HYDE UniversityofMichigan UniversityofCalifornia(Berkeley) NATHAN BALLOU HAROLD KIRBY Navy RadiologicalDefenseLaboratory Mound Laboratory GREGORY R. CHOPPIN GEORGE LEDDICOTTE FloridaStateUniversity Oak RidgeNationalLaboratory GEORGE A. COWAN ELLIS P. STEINBERG Los AlarnosScientificLaboratory Argonne NationalLaboratory ARTHUR W. FAIRHALL PETER C. STEVENSON UniversityofWashington UniversityofCalifornia(Livermore) HARMON FINSTON LEO YAFFE BrookhavenNationalLaboratory McGillUniversity The Radiochemistry of Chromium By J.PIJCK Laboratory for
    [Show full text]
  • The Origin of the Nitrate Ore Fields from the Atacama Desert Revisited: New Insights from the Iodine129 and Stable Chromium Isotopic Systems
    The origin of the nitrate ore fields from the Atacama Desert revisited: New insights from the iodine-129 and stable chromium isotopic systems Alida Pérez Fodich (1,2) , Fernanda Álvarez (1,2) , Martin Reich (1,2) , Glen Snyder (3) , Ronny Schönberg (4) , Gabriel Vargas (1,2) , Carlos Palacios (1) (1) Departamento de Geología, Facultad de Ciencias Físicas y Matemáticas, Universidad de Chile, Santiago, Chile (2) Centro de Excelencia en Geotermia de los Andes, Universidad de Chile, Santiago, Chile (3) Department of Earth Science, Rice University, Houston, Texas, USA (4) Fachbereich Geowissenschaften, Eberhard Karls Universität Tübingen, Tübingen, Germany *E-mail: [email protected] Abstract. Iodine is strongly depleted in the continental the nitrates and soils are the result of the prevalent crust, and due to its large ionic radius it is not incorporated hyperarid climate conditions of the Atacama Desert, with into minerals remaining in the aqueous phase much longer average rainfall rates of less than 10 mm/yr in the last ~3 than other halogens. In the nitrate ore fields of the Atacama Ma (Vargas et al., 2006; Garreaud et al., 2010). Desert of northern Chile, iodine is highly enriched forming The nitrate deposits have been studied in detail for one of the largest reservoirs of iodine in the Earth’s continental crust. However, its occurrence in these deposits decades, and several hypotheses have been proposed for is poorly understood and remains unconstrained. their origin (marine, atmospheric, organic, hydrothermal, In this study, we couple iodine-129 ( 129 I) isotopic with stable etc), (Ericksen, 1981; 1983 and references therein). chromium isotopic ratios ( 53 Cr/ 52 Cr) in chromate-bearing, However the occurrence of iodine and chromium in these iodine-rich nitrate samples.
    [Show full text]
  • Time-Of-Flight Mass Measurements of Neutron-Rich Chromium Isotopes Up
    Time-of-flight mass measurements of neutron-rich chromium isotopes up to N = 40 and implications for the accreted neutron star crust Z. Meisel,1, 2, ∗ S. George,2, 3 S. Ahn,2, 4 D. Bazin,4 B.A. Brown,4, 5 J. Browne,2, 4, 5 J.F. Carpino,6 H. Chung,6 R.H. Cyburt,2, 4 A. Estrad´e,2, 7 M. Famiano,6 A. Gade,4, 5 C. Langer,8 M. Matoˇs,9 W. Mittig,4, 5 F. Montes,2, 4 D.J. Morrissey,4, 10 J. Pereira,2, 4 H. Schatz,2, 4, 5 J. Schatz,4 M. Scott,4, 5 D. Shapira,11 K. Sieja,12 K. Smith,13 J. Stevens,2, 4, 5 W. Tan,1 O. Tarasov,4 S. Towers,6 K. Wimmer,14 J.R. Winkelbauer,4, 5 J. Yurkon,4 and R.G.T. Zegers2, 4, 5 1Department of Physics, University of Notre Dame, Notre Dame, Indiana 46556, USA 2Joint Institute for Nuclear Astrophysics, Michigan State University, East Lansing, Michigan 48824, USA 3Max-Planck-Institut f¨urKernphysik, Heidelberg 69117, Germany 4National Superconducting Cyclotron Laboratory, Michigan State University, East Lansing, Michigan 48824, USA 5Department of Physics and Astronomy, Michigan State University, East Lansing, Michigan 48824, USA 6Department of Physics, Western Michigan University, Kalamazoo, Michigan 49008, USA 7Department of Physics, Central Michigan University, Mount Pleasant, Michigan 48859, USA 8Institute for Applied Physics, Goethe University Frankfurt a. M., Frankfurt a. M. 60438, Germany 9Physics Section, International Atomic Energy Agency, Vienna 1400, Austria 10Department of Chemistry, Michigan State University, East Lansing, Michigan 48824, USA 11Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA 12Universit´ede Strasbourg, IPHC, CNRS, UMR7178, Strasbourg 67037, France 13Department of Physics and Astronomy, University of Tennessee, Knoxville, Tennessee 37996, USA 14Department of Physics, University of Tokyo, Hongo 7-3-1, Bunkyo-ku, Tokyo 113-0033, Japan (Dated: October 21, 2018) We present the mass excesses of 59−64Cr, obtained from recent time-of-flight nuclear mass mea- surements at the National Superconducting Cyclotron Laboratory at Michigan State University.
    [Show full text]
  • Chapter 18 Nuclear Chemistry
    CHAPTER 18 NUCLEAR CHEMISTRY tan is going to visit his son Fred at the radiology department of a local research 18.1 The Nucleus and hospital, where Fred has been recording the brain activity of kids with learning Radioactivity differences and comparing it to the brain activity of kids who excel in normal 18.2 Uses of school environments. To pursue this research, Fred uses imaging technology Radioactive developed through the science of nuclear chemistry, the study of changes that occur Substances within the nuclei of atoms. But even before getting into his car to go see Fred, Stan 18.3 Nuclear Energy is already surrounded by substances undergoing nuclear reactions. In fact, nuclear reactions accompany Stan wherever he goes. He has strontium-90 in his bones and iodine-131 in his thyroid, and both substances are constantly undergoing nuclear reactions of a type known as beta emission. Stan is not unique in this respect. All of our bodies contain these substances and others like them. Stan is surrounded by nuclear changes that take place outside his body, as well. The soil under his house contains a small amount of uranium-238, which undergoes a type of nuclear reaction called alpha emission. A series of changes in the nucleus of the uranium-238 leads to an even smaller amount of radon-222, which is a gas that he inhales in every breath he takes at home. Subsequently, radon-222 undergoes a nuclear reaction very similar to the reaction for uranium-238. On Stan’s way to the hospital, he passes a nuclear power plant that generates electricity for the homes and businesses in his city by means of yet another kind of nuclear reaction.
    [Show full text]
  • Determination of the Relative Thermodynamic Properties of the Iron-Chromium-Nickel System at Temperatures Near 1600° C
    This dissertation has been microfilmed exactly as received 67-2446 GILBY, Stephen Warner, 1939- DETERMINATION OF THE RELATIVE THERMODYNAMIC PROPERTIES OF THE IRON-CHROMIUM-NICKEL SYSTEM AT TEMPERATURES NEAR 1600° C. The Ohio State University, Ph.D., 1966 Engineering, metallurgy University Microfilms, Inc., Ann Arbor, Michigan DETERMINATION OF THE RELATIVE THERMODYNAMIC PROPERTIES OF THE IRON-CHROMIUM-NICKEL SYSTEM AT TEMPERATURES NEAR l6 0 0 °C , DISSERTATION Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio S ta te U n iv e rsity By Stephen Warner Gilby, B.S. The Ohio S ta te U n iv e rsity 1966 Approved by Department of M etallurgical Engineering ACKNOWLEDGMENTS The author gratefully acknowledges the assistance of Dr. George R. St.Pierre whose guidance and thoughtful comments aided greatly in the completion of this thesis. The experimental assistance of Dr. Rudolph Speiser is also greatly appreciated. The author would especially like to thank Mr. Richard Reese for his able assistance in collecting and analyzing the mass spectrometer data reported in this thesis. The valuable assistance of Dr. Karl Svank is also acknowledged. The financial support of the American Iron and Steel Institute and the International Nickel Company made this thesis p ossib le. i i CONTENTS Page ACKNOWLEDGMENTS i i TABLES iv FIGURES v i INTRODUCTION AND UTERATURE REVIEW 1 EXPERIMENTAL EQUIPMENT 25 THEORETICAL BASIS ia EXPERIMENTAL PROCEDURE 5o RESULTS AND DISCUSSION 77 APPENDIXES 1UU BIBLIOGRAPHY 171 i i i TABLES Table Page 1. The Relative Isotopic Abundances of the Isotopes of .
    [Show full text]