DOCSLIB.ORG

Units and Dimensions

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Units and Dimensions Appendix A Units and Dimensions It is essential to distinguish between units and dimensions. Broadly speaking, physical parameters have the separate properties of size and dimension. A unit is a, more or less arbitrarily defined, amount or quantity in terms of which a parameter is defined. A dimension represents the definition of an inherent property, independent of the system of units in which it is expressed. For example, the dimension mass expresses the amount of material of which a body is constructed, the distance between the wing tips (wingspan) of an aeroplane has the dimension length. The mass of a body can be expressed in kilograms or in pounds, the wingspan can be expressed in metres or in feet. Many systems of units exist, each of which with their own advantages and drawbacks. Throughout this book the internationally accepted dynamical system SI is used, except in a few places as specially noted. The Imperial set of units still plays an important roll in aviation, in particular in the United States. Fundamental dimensions and units Dimensions can be written in symbolic form by placing them between square brackets. There are four fundamental units in terms of which the dimensions of all other physical quantities may be expressed. Purely mechanical rela- tionships are derived in terms of mass [M], length [L], and time [T]; thermo- dynamical relationships contain the temperature [θ] as well. A fundamental equation governing dynamical systems is derived from Newton’s second law of motion. This states that an external force F acting on a body is proportional to the product of its mass m and the acceleration a produced by the force: F = kF ma. The constant of proportionality kF is de- 511 512 A Units and Dimensions Table A.1 Dimensions and SI units used for dynamical systems. Quantity Dimension Unit name Symbol Explanation length [L] metre m fundamental unit mass [M] kilogram kg fundamental unit time [T] second s fundamental unit area [L2]– m2 length×length volume [L3]– m3 area×length velocity [LT−1]– ms−1 length/time acceleration [LT−2]– ms−2 velocity/time moment of inertia [ML2]– kgm2 mass×area density [ML−3]– kgm−3 mass/volume mass flow rate [MT−1]– kgs−1 mass/time force [MLT−2]NewtonN,kgms−2 mass×acceleration moment [ML2T−2] – N m force×length pressure, stress [ML−1T−2] Pascal Pa, N m−2 force/area momentum [MLT−1]– Ns,kgms−1 mass×velocity momentum flow [MLT−2]– N,kgms−2 mass×velocity/time work or energy [ML2T−2] Joule J, N m force×length power [ML2T−3]Watt W,Nms−1 work or energy/time angle 1 radian rad length/length angular velocity [T−1]– rads−1 angle/time angular acceleration [T−2]– rads−2 angular velocity/time frequency [T−1] Hertz Hz 1/time termined by the definition of the units of force, mass and acceleration used in the equation. In general, if the system of units is changed, so also is the constant kF . It is useful, of course, to select the units so that the equation becomes F = ma.Inaconsistent system of units, the force, mass, and time are defined so that kF = 1. For this to be true, the unit of force has to be that force which, when acting upon a unit mass, produces a unit acceleration. International System of Units In most parts of the world the Système International d’Unités, commonly abbreviated to SI units, is accepted for most branches of science and engi- neering. The SI system uses the following fundamental units: Flight Physics 513 • Mass: the kilogram (symbol kg) is equivalent to the international stan- dard held in Sèvres near Paris. • Length: the metre (symbol m), preserved in the past as a prototype, is presently defined as the distance (m) travelled by light in a vacuum in 299,792,458−1 seconds. • Time: the second (symbol s) is the fundamental unit of time, defined in terms of the natural periodicity of the radiation of a cesium-133 atom. • Temperature: the unit Kelvin (symbol K) is identical in size with the degree Celsius (symbol ◦C), but it denotes the absolute (or thermody- namical) temperature, measured from the absolute zero. The degree Cel- sius is one hundredth part of the temperature rise involved when pure water is heated from the triple point (273.15 K) to boiling temperature at standard pressure. The temperature in degrees Celsius is therefore T (C) = T (K) − 273.15. Having defined the four fundamental dimensions and their units, all other physical quantities can be established, as in Table A.1. Velocity, for exam- ple, is defined as the distance travelled in unit time. It has the dimension [LT−1] and is measured in metres per second (m s−1, or m/s). The following additional remarks are made in relation to Table A.1: • The SI system defines the Newton (symbol N) as the fundamental unit for force, imparting an acceleration of 1 m s−2 to one kilogram of mass. From Newton’s equation, its dimension is derived as [MLT−2]. By con- trast to some other systems of units, the definition of a newton is com- pletely unrelated to the acceleration due to gravity. Clearly, the SI system forms a consistent system. • The fundamental unit of (gas) pressure or (material) stress is denoted pascal (symbol Pa). The bar is defined as 105 Pa, the millibar1 (mb) amounts to 102 Pa. A frequently used alternative unit of gas pressure is the physical atmosphere (symbol atm), which is equal to the pressure un- der a 760 mm high column of mercury: 1.01325 × 105 Pa. The standard atmosphere is set at an air pressure of 1 atm at sea level. The techni- cal atmosphere (symbol at) is equal to the pressure under a 10 m high column of water, g × 104 Pa. This requires a definition of the accelera- tion due to gravity, which is taken as the value at 45◦ northern latitude: g = 9.80665 m s−2. • The (dimensionless) radian is defined as the angle subtended at the centre of a circle by an arc equal in length to the radius. One radian is equal to 180/π = 57.296◦. 1 The preferred symbol is the hectopascal, hPa. 514 A Units and Dimensions Fractions and multiples Sometimes, the fundamental units defined above are inconveniently large or small for a particular case. In such cases, the quantity can be expressed in terms of some fraction or multiple of the fundamental unit. A prefix attached to a unit makes a new unit. The following prefixes may be used to indicate decimal fractions or multiples of SI units. Fraction Prefix Symbol Multiple Prefix Symbol 10−1 deci d 10 deca da 10−2 centi c 102 hecto h 10−3 milli m 103 kilo k 10−6 micro µ 106 mega M Imperial units Until about 1968, the Imperial (or British Engineering) set of units was in use in some parts of the world, the United Kingdom in particular. It uses the fundamental units foot (symbol ft) for length and pound (symbol lbm) for mass, the unit for time is the second. The corresponding unit for force, the poundal, produces an acceleration of 1 ft s−2 to 1 lbm. The Imperial System is therefore a consistent one. Since the poundal is considered as an unpracti- cally small force, it is often replaced by the pound force (symbol lbf), which is defined as the weight of one pound mass. The pound force is therefore g times as large as the poundal. However, used with 1 pound mass and 1 ft s−2, it does not constitute a consistent set of units. Therefore, the slug has been defined as a mass equal to g times the pound mass, dictating that a standard value is used for the acceleration due to gravity (32.174 ft s−2). The Imperial system uses the Kelvin or the degree Celsius (“centigrade”) as the standard unit of temperature. Although the SI system constitutes the generally accepted international standard, many Imperial units are still in use, especially in the practice of aircraft operation and in the US engineering world. For example, use is still made of the temperature scales Fahrenheit (F) and Rankine (R). The Rankine is an absolute temperature coupled to the Fahrenheit scale and is not to be confused with the former Réaumur temperature unit. The conversion from degrees Fahrenheit to Kelvin is as follows: T (K) = 273.15 + 5/9{T (F) − 32}. The system of units based on the foot, pound, second and rankine is Flight Physics 515 Table A.2 Table for converting British FPSR units into SI units. Quantity Symbol Multiply by to obtain SI units length inch (in) 2.54 × 10−2 m foot (ft = 12 in) 3.048 × 10−1 m mile 1.6093 km nautical mile (nm) 1.8532 km volume cubic ft 2.8317 × 10−2 m3 UK gallon 4.5461 × 10−3 m3 US gallon 3.7854 × 10−3 m3 velocity ft/s 3.048 × 10−1 m/s mile/h 1.609 km/h UK knot = nm/h 1.853 km/h mass slug 1.4594 × 10 kg pound mass (lbm) 4.5359 × 10−1 kg UK ton 1.0165 × 103 kg US short ton 9.0718 × 102 kg force pound force (lbf) 4.4482 N poundal 1.3826 × 10−1 N pressure lbf/in2 (psi) 6.8948 × 103 Pa lbf/ft2 (psf) 4.7880 × 10 Pa temperature Rankine (R) 5/9 K work ft lbf 1.355 Nm energy BTU 1.055 × 103 J specific energy BTU/slug 7.2290 × 10 Nm/kg power slug ft2/s3 1.356 Nm/s horsepower∗ (hp) 7.457 × 102 W viscosity coefficient slug/ft/s 4.788 × 10 kg/m/s kinematic viscosity ft2/s 9.290 × 10−2 m2/s ∗The unit of power in the (former) Technical System of Units is also known as the (metric) horsepower.
Load more

Recommended publications
  • Che 253M Experiment No. 2 COMPRESSIBLE GAS FLOW
    Rev. 8/15 AD/GW ChE 253M Experiment No. 2 COMPRESSIBLE GAS FLOW The objective of this experiment is to familiarize the student with methods for measurement of compressible gas flow and to study gas flow under subsonic and supersonic flow conditions. The experiment is divided into three distinct parts: (1) Calibration and determination of the critical pressure ratio for a critical flow nozzle under supersonic flow conditions (2) Calculation of the discharge coefficient and Reynolds number for an orifice under subsonic (non- choked) flow conditions and (3) Determination of the orifice constants and mass discharge from a pressurized tank in a dynamic bleed down experiment under (choked) flow conditions. The experimental set up consists of a 100 psig air source branched into two manifolds: the first used for parts (1) and (2) and the second for part (3). The first manifold contains a critical flow nozzle, a NIST-calibrated in-line digital mass flow meter, and an orifice meter, all connected in series with copper piping. The second manifold contains a strain-gauge pressure transducer and a stainless steel tank, which can be pressurized and subsequently bled via a number of attached orifices. A number of NIST-calibrated digital hand held manometers are also used for measuring pressure in all 3 parts of this experiment. Assorted pressure regulators, manual valves, and pressure gauges are present on both manifolds and you are expected to familiarize yourself with the process flow, and know how to operate them to carry out the experiment. A process flow diagram plus handouts outlining the theory of operation of these devices are attached.
    [Show full text]
  • Appendix A: Symbols and Prefixes
    Appendix A: Symbols and Prefixes (Appendix A last revised November 2020) This appendix of the Author's Kit provides recommendations on prefixes, unit symbols and abbreviations, and factors for conversion into units of the International System. Prefixes Recommended prefixes indicating decimal multiples or submultiples of units and their symbols are as follows: Multiple Prefix Abbreviation 1024 yotta Y 1021 zetta Z 1018 exa E 1015 peta P 1012 tera T 109 giga G 106 mega M 103 kilo k 102 hecto h 10 deka da 10-1 deci d 10-2 centi c 10-3 milli m 10-6 micro μ 10-9 nano n 10-12 pico p 10-15 femto f 10-18 atto a 10-21 zepto z 10-24 yocto y Avoid using compound prefixes, such as micromicro for pico and kilomega for giga. The abbreviation of a prefix is considered to be combined with the abbreviation/symbol to which it is directly attached, forming with it a new unit symbol, which can be raised to a positive or negative power and which can be combined with other unit abbreviations/symbols to form abbreviations/symbols for compound units. For example: 1 cm3 = (10-2 m)3 = 10-6 m3 1 μs-1 = (10-6 s)-1 = 106 s-1 1 mm2/s = (10-3 m)2/s = 10-6 m2/s Abbreviations and Symbols Whenever possible, avoid using abbreviations and symbols in paragraph text; however, when it is deemed necessary to use such, define all but the most common at first use. The following is a recommended list of abbreviations/symbols for some important units.
    [Show full text]
  • American and BRITISH UNITS of Measurement to SI UNITS
    AMERICAN AND BRITISH UNITS OF MEASUREMENT TO SI UNITS UNIT & ABBREVIATION SI UNITS CONVERSION* UNIT & ABBREVIATION SI UNITS CONVERSION* UNITS OF LENGTH UNITS OF MASS 1 inch = 40 lines in 2.54 cm 0.393701 1 grain gr 64.7989 mg 0.0154324 1 mil 25.4 µm 0.03937 1 dram dr 1.77185 g 0.564383 1 line 0.635 mm 1.57480 1 ounce = 16 drams oz 28.3495 g 0.0352739 1 foot = 12 in = 3 hands ft 30.48 cm 0.0328084 1 pound = 16 oz lb 0.453592 kg 2.204622 1 yard = 3 feet = 4 spans yd 0.9144 m 1.09361 1 quarter = 28 lb 12.7006 kg 0.078737 1 fathom = 2 yd fath 1.8288 m 0.546807 1 hundredweight = 112 lb cwt 50.8024 kg 0.0196841 1 rod (perch, pole) rd 5.0292 m 0.198839 1 long hundredweight l cwt 50.8024 kg 0.0196841 1 chain = 100 links ch 20.1168 m 0.0497097 1 short hundredweight sh cwt 45.3592 kg 0.0220462 1 furlong = 220 yd fur 0.201168 km 4.97097 1 ton = 1 long ton tn, l tn 1.016047 t 0.984206 1 mile (Land Mile) mi 1.60934 km 0.62137 1 short ton = 2000 lb sh tn 0.907185 t 1.102311 1 nautical mile (intl.) n mi, NM 1.852 km 0.539957 1 knot (Knoten) kn 1.852 km/h 0.539957 UNITS OF FORCE 1 pound-weight lb wt 4.448221 N 0.2248089 UNITS OF AREA 1 pound-force LB, lbf 4.448221 N 0.2248089 1 square inch sq in 6.4516 cm2 0.155000 1 poundal pdl 0.138255 N 7.23301 1 circular inch 5.0671 cm2 0.197352 1 kilogram-force kgf, kgp 9.80665 N 0.1019716 1 square foot = 144 sq in sq ft 929.03 cm2 1.0764 x 10-4 1 short ton-weight sh tn wt 8.896444 kN 0.1124045 1 square yard = 9 sq ft sq yd 0.83613 m2 1.19599 1 long ton-weight l tn wt 9.964015 kN 0.1003611 1 acre = 4 roods 4046.8
    [Show full text]
  • Having Regard to the Opinion of the European Chapter 1 of the Annex Binding Within Five Years of Parliament1 ; the Date of Entry Into Force of This Directive
    878 Official Journal of the European Communities 29.10.71 Official Journal of the European Communities No L 243/29 COUNCIL DIRECTIVE of 18 October 1971 on the approximation of the laws of the Member States relating to units of measurement (71/354/EEC ) THE COUNCIL OF THE EUROPEAN COMMUNITIES, particular their names, symbols and use are not identical in the Member countries ; Having regard to the Treaty establishing the European Economic Community, and in particular HAS ADOPTED THIS DIRECTIVE : Article 100 thereof; Article 1 Having regard to the proposal from the Commission ; 1 . Member States shall make the provisions of Having regard to the Opinion of the European Chapter 1 of the Annex binding within five years of Parliament1 ; the date of entry into force of this Directive. 2 . Member States shall, with effect from 31 Having regard to the Opinion of the Economic and December 1977 at the latest, prohibit the use of the Social Committee2; units of measurement listed in Chapter III of the Annex. Whereas - the laws which regulate the use of units of measurement in the Member States differ from one 3 . The units of measurement temporarily" retained Member State to another and therefore hinder trade ; in accordance with the provisions of Chapter II or whereas application of the rules relating to measuring Chapter III of the Annex may not be brought into instruments is closely linked to the use of units of compulsory use by the Member States where they ' are measurement in the metrological system ; whereas, in not authorised at the date when this Directive enters into force .
    [Show full text]
  • Aspects of Flow for Current, Flow Rate Is Directly Proportional to Potential
    Vacuum technology Aspects of flow For current, flow rate is directly proportional to potential difference and inversely proportional to resistance. I = V/R or I = V/R For a fluid flow, Q = (P1-P2)/R or P/R Using reciprocal of resistance, called conductance, we have, Q = C (P1-P2) There are two kinds of flow, volumetric flow and mass flow Volume flow rate, S = vA v – the average bulk velocity, A the cross sectional area S = V/t, V is the volume and t is the time. Mass flow rate is S x density. G = vA or V/t Mass flow rate is measured in units of throughput, such as torr.L/s Throughput = volume flow rate x pressure Throughput is equivalent to power. Torr.L/s (g/cm2)cm3/s g.cm/s J/s W It works out that, 1W = 7.5 torr.L/s Types of low 1. Laminar: Occurs when the ratio of mass flow to viscosity (Reynolds number) is low for a given diameter. This happens when Reynolds number is approximately below 2000. Q ~ P12-P22 2. Above 3000, flow becomes turbulent Q ~ (P12-P22)0.5 3. Choked flow occurs when there is a flow restriction between two pressure regions. Assume an orifice and the pressure difference between the two sections, such as 2:1. Assume that the pressure in the inlet chamber is constant. The flow relation is, Q ~ P1 4. Molecular flow: When pressure reduces, MFP becomes larger than the dimensions of the duct, collisions occur between the walls of the vessel.
    [Show full text]
  • Guide for the Use of the International System of Units (SI)
    Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S.
    [Show full text]
  • 4.1 – Radian and Degree Measure
    4.1 { Radian and Degree Measure Accelerated Pre-Calculus Mr. Niedert Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 1 / 27 2 Radian Measure 3 Degree Measure 4 Applications 4.1 { Radian and Degree Measure 1 Angles Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 2 / 27 3 Degree Measure 4 Applications 4.1 { Radian and Degree Measure 1 Angles 2 Radian Measure Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 2 / 27 4 Applications 4.1 { Radian and Degree Measure 1 Angles 2 Radian Measure 3 Degree Measure Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 2 / 27 4.1 { Radian and Degree Measure 1 Angles 2 Radian Measure 3 Degree Measure 4 Applications Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 2 / 27 The starting position of the ray is the initial side of the angle. The position after the rotation is the terminal side of the angle. The vertex of the angle is the endpoint of the ray. Angles An angle is determine by rotating a ray about it endpoint. Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 3 / 27 The position after the rotation is the terminal side of the angle. The vertex of the angle is the endpoint of the ray. Angles An angle is determine by rotating a ray about it endpoint. The starting position of the ray is the initial side of the angle. Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 3 / 27 The vertex of the angle is the endpoint of the ray.
    [Show full text]
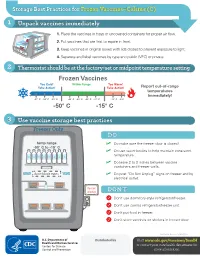
  • Storage Best Practices for Frozen Vaccines-Celsius
    Storage Best Practices for Frozen Vaccines–Celsius (C) 1 Unpack vaccines immediately 1. Place the vaccines in trays or uncovered containers for proper air flow. 2. Put vaccines that are first to expire in front. HEP A - VFC 3. Keep vaccines in original boxes with lids closed to prevent exposure to light. 4. Separate and label vaccines by type and public (VFC) or private. 2 Thermostat should be at the factory-set or midpoint temperature setting Frozen Vaccines Too Cold! Within Range Too Warm! Take Action! Take Action! Report out-of-range temperatures immediately! -57° C -54° C -51° C -46° C -43° C -40° C -37° C -12° C -9°C -50° C -15° C 3 Use vaccine storage best practices Freezer Only DO temp range ✓ Do make sure the freezer door is closed! -50° C to -15° C ✓ Do use water bottles to help maintain consistent temperature. ✓ Do leave 2 to 3 inches between vaccine containers and freezer walls. don’t block vents ✓ Do post “Do Not Unplug” signs on freezer and by electrical outlet. do not unplug DON’T Don’t use dormitory-style refrigerator/freezer. Don’t use combo refrigerator/freezer unit. Don’t put food in freezer. Don’t store vaccines on shelves in freezer door. CS243541-D Revision %FDFNCFS 20 Distributed by Visit www.cdc.gov/vaccines/SandH or contact your state health department for more information. Test Your Knowledge 1 Which of the following units is the best for storing frozen vaccines? Freezer Freezer Freezer Freezer A. Full-size B. Full-size C.
    [Show full text]
  • Relationships of the SI Derived Units with Special Names and Symbols and the SI Base Units
    Relationships of the SI derived units with special names and symbols and the SI base units Derived units SI BASE UNITS without special SI DERIVED UNITS WITH SPECIAL NAMES AND SYMBOLS names Solid lines indicate multiplication, broken lines indicate division kilogram kg newton (kg·m/s2) pascal (N/m2) gray (J/kg) sievert (J/kg) 3 N Pa Gy Sv MASS m FORCE PRESSURE, ABSORBED DOSE VOLUME STRESS DOSE EQUIVALENT meter m 2 m joule (N·m) watt (J/s) becquerel (1/s) hertz (1/s) LENGTH J W Bq Hz AREA ENERGY, WORK, POWER, ACTIVITY FREQUENCY second QUANTITY OF HEAT HEAT FLOW RATE (OF A RADIONUCLIDE) s m/s TIME VELOCITY katal (mol/s) weber (V·s) henry (Wb/A) tesla (Wb/m2) kat Wb H T 2 mole m/s CATALYTIC MAGNETIC INDUCTANCE MAGNETIC mol ACTIVITY FLUX FLUX DENSITY ACCELERATION AMOUNT OF SUBSTANCE coulomb (A·s) volt (W/A) C V ampere A ELECTRIC POTENTIAL, CHARGE ELECTROMOTIVE ELECTRIC CURRENT FORCE degree (K) farad (C/V) ohm (V/A) siemens (1/W) kelvin Celsius °C F W S K CELSIUS CAPACITANCE RESISTANCE CONDUCTANCE THERMODYNAMIC TEMPERATURE TEMPERATURE t/°C = T /K – 273.15 candela 2 steradian radian cd lux (lm/m ) lumen (cd·sr) 2 2 (m/m = 1) lx lm sr (m /m = 1) rad LUMINOUS INTENSITY ILLUMINANCE LUMINOUS SOLID ANGLE PLANE ANGLE FLUX The diagram above shows graphically how the 22 SI derived units with special names and symbols are related to the seven SI base units. In the first column, the symbols of the SI base units are shown in rectangles, with the name of the unit shown toward the upper left of the rectangle and the name of the associated base quantity shown in italic type below the rectangle.
    [Show full text]
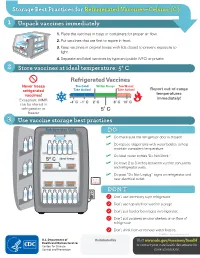
  • Storage Best Practices for Refrigerated Vaccines–Celsius (C)
    Storage Best Practices for Refrigerated Vaccines–Celsius (C) 1 Unpack vaccines immediately 1. Place the vaccines in trays or containers for proper air flow. 2. Put vaccines that are first to expire in front. HEP A - VFC 3. Keep vaccines in original boxes with lids closed to prevent exposure to light. 4. Separate and label vaccines by type and public (VFC) or private. 2 Store vaccines at ideal temperature: 5° C Refrigerated Vaccines Never freeze Too Cold! Within Range Too Warm! refrigerated Take Action! Take Action! Report out-of-range vaccines! temperatures Exception: MMR immediately! -4˚ C -1˚ C 2˚ C 8˚ C 10˚ C can be stored in refrigerator or 5˚ C freezer 3 Use vaccine storage best practices Refrigerator Only DO ✓ Do make sure the refrigerator door is closed! ✓ Do replace crisper bins with water bottles to help maintain consistent temperature. ✓ Do label water bottles "Do Not Drink." 5° C ideal temp ✓ Do leave 2 to 3 inches between vaccine containers and refrigerator walls. ✓ Do post “Do Not Unplug” signs on refrigerator and do not near electrical outlet. unplug DON’T ; Don’t use dormitory-style refrigerator. ; Don’t use top shelf for vaccine storage. ; Don’t put food or beverages in refrigerator. ; Don’t put vaccines on door shelves or on floor of refrigerator. Don’t drink from or remove water bottles. ; CS243541-C Revision February 2018 Distributed by Visit www.cdc.gov/vaccines/SandH or contact your state health department for more information. Test Your Knowledge 1 Can you find at least 8 things that are wrong with vaccine storage in this refrigerator? 5° C ideal temp 2 When unpacking vaccines, why is it important to put the first-to-expire in the front? A.
    [Show full text]
  • Mass Flow Rate and Isolation Characteristics of Injectors for Use with Self-Pressurizing Oxidizers in Hybrid Rockets
    49th AIAA/ASME/SAE/ASEE Joint PropulsionConference AIAA 2013-3636 July 14 - 17, 2013, San Jose, CA Mass Flow Rate and Isolation Characteristics of Injectors for Use with Self-Pressurizing Oxidizers in Hybrid Rockets Benjamin S. Waxman*, Jonah E. Zimmerman†, Brian J. Cantwell‡ Stanford University, Stanford, CA 94305 and Gregory G. Zilliac§ NASA Ames Research Center, Moffet Field, CA 94035 Self-pressurizing rocket propellants are currently gaining popularity in the propulsion community, partic- ularly in hybrid rocket applications. Due to their high vapor pressure, these propellants can be driven out of a storage tank without the need for complicated pressurization systems or turbopumps, greatly minimizing the overall system complexity and mass. Nitrous oxide (N2O) is the most commonly used self pressurizing oxidizer in hybrid rockets because it has a vapor pressure of approximately 730 psi (5.03 MPa) at room temperature and is highly storable. However, it can be difficult to model the feed system with these propellants due to the presence of two-phase flow, especially in the injector. An experimental test apparatus was developed in order to study the performance of nitrous oxide injectors over a wide range of operating conditions. Mass flow rate characterization has been performed to determine the effects of injector geometry and propellant sub-cooling (pressurization). It has been shown that rounded and chamfered inlets provide nearly identical mass flow rate improvement in comparison to square edged orifices. A particular emphasis has been placed on identifying the critical flow regime, where the flow rate is independent of backpressure (similar to choking). For a simple orifice style injector, it has been demonstrated that critical flow occurs when the downstream pressure falls sufficiently below the vapor pressure, ensuring bulk vapor formation within the injector element.
    [Show full text]
  • Whose- U&XD0(4 Rr ? S. Pei^ Usow
    whose- U&XD 0(4 rr ? ¿ 5 S. p e i^ usow OST of us have invented a country, oerhaps a philosoph­ ically constructed "Republic" or "Utopia", perhaps just a fictional world of our own. The country we invent will reflect our thoughts, just as the 'Lord or the Rings' and 'The Silmarillion' reveal Tolkien's ideas and ideals. Inventing a country - or what is equivalent - writing a fantasy or science-fiction story, creates certain problems. In writing a fantasy story we need to invent a certain amount. A few 'alien' versions of everyday necessities - such as currency or weights and measures - are sufficient to tell the reader that the story is not an everyday one; but invent too many words or new ideas and we risk pushing our story too far away from our audience for them to treat it as anything more than 'just' fiction. In this article I wish to look at one aspect of the fantasy world (or secondary world, if you prefer): the metrology, and its role in the 'Lord of the Rings' in particular. Why metrology? Perhaps for no better reason than that metrication is upon us. For better or for worse our world is being changed, like it or not; it is not simply another necessary change; it creates a barrier between the past and the future. Fantasy writers sometimes mention metrology; Burroughs., on Barsoom, provided footnotes on the measure used on Mars, on the time-units, and also on the measures on Venus. Not all writers go to this extreme; some mention time-units to make the point that a non-decimal system is being used, others may say nothing at all, taking it for granted that the metric system is in uni­ versal use.
    [Show full text]