Heuristics for Delay Management with Re-Routing
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Amsterdam City Doughnut
THE AMSTERDAM CITY DOUGHNUT A TOOL FOR TRANSFORMATIVE ACTION TABLE OF CONTENTS Amsterdam becoming a thriving city 3 The Doughnut: a 21st century compass 4 Creating a Thriving City Portrait 5 Amsterdam’s City Portrait 6 Lens 1: Local Social 6 What would it mean for the people of Amsterdam to thrive? Lens 2: Local Ecological 8 What would it mean for Amsterdam to thrive within its natural habitat? Lens 3: Global Ecological 10 What would it mean for Amsterdam to respect the health of the whole planet? Lens 4: Global Social 12 What would it mean for Amsterdam to respect the wellbeing of people worldwide? The City Portrait as a tool for transformative action 14 1. From public portrait to city selfie 16 2. New perspectives on policy analysis 17 Principles for putting the Doughnut into practice 18 References 20 8 WAYS TO TURN THE CITY PORTRAIT How can Amsterdam be a home to thriving people, INTO TRANSFORMATIVE ACTION AMSTERDAM BECOMING in a thriving place, while respecting the wellbeing A THRIVING CITY of all people, and the health of the whole planet? MIRROR Reflect on the current Cities have a unique role and opportunity to shape humanity’s The Amsterdam City Doughnut is intended as a stimulus for state of the city through chances of thriving in balance with the living planet this cross-departmental collaboration within the City, and for the portrait’s holistic century. As home to 55% of the world’s population, cities connecting a wide network of city actors in an iterative process perspective account for over 60% of global energy use, and more than of change, as set out in the eight ‘M’s on the right. -

The German Occupation and the Persecution of the Jews in Diemen
The German occupation and the persecution of the Jews in Diemen The role of the municipal administration, collaboration and labour camp Betlem Roos Smit 5957249 MA thesis in History - Holocaust and Genocide Studies, University of Amsterdam Supervisor: Dr. K. Berkhoff Second reader: Prof. Dr. Johannes ten Cate June 2018 2 Content 1. Introduction 2 2. The Municipality Diemen: the mayor 7 2.1 Mayors 8 2.2 Mayor de Geer van Oudegein before the occupation 10 2.3 In charge of mayors: secretary-General K.J. Frederiks 12 2.4 Mayor de Geer van Oudegein during the occupation 14 2.5 The destruction of the Diemerkade 17 2.6 Mayors of Diemen after de Geer van Oudegein 19 3. The Municipality Diemen: the municipal secretary 21 3.1 The diary of Mr. van Silfhout 21 3.2 Other acts by Mr. van Silfhout 25 4. Mr. F.B. Schröder 28 4.1 Mr. Schröder 1879-1940 28 4.2 Mr. Schröder 1940-1945 29 4.3 Mr. Schröder 1945-1949 35 5. Betlem 42 5.1 Labour camps 42 5.2 Labour camp Betlem 48 6. Conclusion 55 7. Bibliography 58 7.1 Resources 58 7.2 Literature 59 1 2 1. Introduction Diemen, a small municipality under Amsterdam, believes that they have always had a special relationship with the Dutch Royal House of Orange. Queen Wilhelmina loved to meander in Diemen and Prince Bernhard crashed his car there. From 1899 onwards Diemen held the Oranjefeesten: multiple days of festivities mostly for the Diemer children.1 In this thesis, we will see that many protagonists from Diemen share that loyalty to the house of Orange. -

Convenant Verduurzaming Stadsverwarmingscentrale Diemen
CONVENANT VERDUURZAMING STADSVERWARMINGSCENTRALE DIEMEN. De gemeente Diemen, De gemeente Almere, De gemeente Amsterdam, De gemeente Weesp, De gemeente Gooise Meren, De provincie Noord Holland, Vattenfall Power Generation BV, verder te noemen Vattenfall, verder te noemen “Partijen” komen ten aanzien van de verduurzaming van de warmtelevering vanuit de Stadsverwarmingscentrale te Diemen en daarmee samenhangende aspecten het volgende overeen. Preambule Vattenfall heeft de ambitie om binnen één generatie fossielvrij leven mogelijk te maken en betrekt daar haar klanten, haar toeleveranciers en overheden in. Deze ambitie is onder meer vertaald in een strategie ter verduurzaming van de Diemense Stadsverwarmingscentrale en het daaraan gekoppelde stadsverwarmingsnet in Amsterdam, Diemen en Almere. Momenteel reduceert dit stadverwarmingssysteem de CO2 emissies met ca 50% in vergelijking tot individuele gasketels bij de mensen thuis. Voor 2040 is het uitganspunt dat geheel fossielvrij warmte wordt geproduceerd, onder gelijktijdig forse groei van het aantal aansluitingen. Daarbij wordt ingezet op grootschalige toepassing van een mix van duurzame energiebronnen, zoals Geothermie, Aquathermie, Restwarmte uit Datacenters, groene waterstof en elektriciteit voor warmteopwekking (“power to heat”), Daarnaast wordt op korte termijn ingezet op het gebruik van Houtpellets, te stoken in een daarvoor te realiseren Biomassainstallatie. Deze biomassa wordt benut als transitiebrandstof. Na de eerste 12 jaar wordt het gebruik van biomassa geleidelijk weer afgebouwd, waarbij de andere genoemde bronnen de rol geleidelijk overnemen van zowel het nog resterende gasverbruik als de biomassa. Over het gebruik van biomassa voor energielevering bestaat een, soms felle, maatschappelijke discussie. Daarbij willen wij opmerken dat de oorsprong van deze discussie ligt bij het grootschalig gebruik van biomassa voor elektriciteitsproductie, waarvoor het overgrote deel van de in Nederland geïmporteerde biomassa wordt gebruikt. -

Amsterdam Metro
AMSTERDAM METRO CONNECT TO AMS-IX, NL-IX, VANCIS AND NIKHEF THROUGH AWARD-WINNING, GREEN, ENERGY-EFFICIENT DATA CENTERS AT-A-GLANCE Our Amsterdam data centers are business AM8 For enterprises Westpoort hubs for 1,130+ companies. Equinix’s Amsterdam-Noord A5 • Ability to reach 80% of Europe within Amsterdam customers can choose from A10 50 ms makes this location ideal for a broad range of network services from A10 enterprises. 180+ providers. They can also interconnect Amsterdam AM3/AM4 ® to customers and partners in their digital Amsterdam • Performance Hub enables next- Nieuw-West supply chain. Amsterdam-Oost generation Wide Area Network (WAN) AM6 A1 architecture for secure and highly Our Amsterdam data centers offer state- A4 A10 Diemen reliable connectivity to 180+ network Amsterdam-Zuid Equinix AM3 IBX data center exterior of-the-art colocation services providing service providers and 440+ cloud and plenty of available capacity for now and IT services providers. A2 Amsterdam-Zuidoost in the future. We host connectivity to Amstelveen AM11 AM1 • On-demand and direct access to multiple cloud providers via Equinix Cloud major cloud service providers that include AM7 AM2 AM5 Exchange Fabric™ (ECX Fabric™). AWS, Microsoft Azure, IBM Softlayer A9 and Google Cloud. Customers at our For cloud and IT services providers Amsterdam colocation facilities can take advantage of peering opportunities with • Ideal entry point for cloud providers establishing presence in Europe with direct our own Equinix Internet Exchange™, as well as the Amsterdam Internet Exchange access to hundreds of carriers and diverse ecosystems. (AMS-IX) and the Neutral Internet Exchange (NL-ix), where approximately 1000 ISPs, telecommunications carriers, content providers and hosting services from all over the • Powered by ECX Fabric for direct, cost-effective, secure consumption and delivery world interconnect. -

1 Inholland University of Applied Sciences Amsterdam/Diemen Date: See Postmark Contact: Angelique Schipper Subject: IT/IBMS/LM/T
INHolland University of Applied Sciences Amsterdam/Diemen Date: See postmark Contact: Angelique Schipper Subject: IT/IBMS/LM/TRM 2010/2011 Telephone: +31 (0)20 495 1543 Reference: IT/IBMS/LM/TRM -info pack letter Fax: +31 (0)20 495 1947 E-mail: [email protected] To: Applicants of the English stream programs Dear Madam / Sir, Thank you for your enquiry about our English stream programs at INHolland University of Applied Sciences. The following courses are offered as English stream programs: Information Technology (IT) International Business and Management Studies (IBMS) (Full Time, Part Time and Fast Track) Leisure Management (LM) Tourism and Recreation Management (TRM) For more detailed information on admission requirements we have included our enrolment procedure. All programs will start late August/beginning of September 2010. If there are sufficient numbers of applicants, a spring semester of the IBMS FT/ PT course (beginning of February 2011), will also be held. We hope that this information helps you to plan your further education. Yours faithfully, Angelique Schipper International Recruitment Office IT/IBMS/LM/TRM Enclosed: 1) Admission Requirements 2) Enrolment Procedure 3) Check list 1 Admission Requirements All Students will have to complete the following steps in order to successfully enroll to one of the English stream programs: 1. Registration with INHolland and CBAP (IBG) In order to enroll into higher education in The Netherlands, every student has to enroll with “Studielink”. You can register to Studielink through the following link: http://www.inholland.nl/INHOLLANDCOM/Studying+at+INHOLLAND/Application+in+Studielin k/Application.htm In order to register with Studielink, you will need one of the following course codes: . -

Van Concept RES Naar RES 1.0 Achtergrondnotitie Bij De Herziening Van De Diemense Zoekgebieden Voor Wind En Zon
Van Concept RES naar RES 1.0 Achtergrondnotitie bij de herziening van de Diemense zoekgebieden voor wind en zon Gemeente Diemen, 15 februari 2021 Inhoudsopgave 1. Inleiding ................................................................................................................................... 3 2. Toelichting afwegingskaders en opgehaalde informatie en perspectieven .................................. 3 2.1 Kwantiteit elektriciteit ................................................................................................................... 3 2.2 Ruimtegebruik ............................................................................................................................... 4 2.3 Bestuurlijk en maatschappelijk draagvlak ..................................................................................... 5 2.4 Energiesysteemefficiëntie ............................................................................................................. 7 2.5 Effectenmatrix voor integrale afweging ........................................................................................ 7 3. Inzichten en bijzonderheden per zoekgebied ............................................................................. 8 3.1 Diemer Vijfhoek (zoekgebied wind) .............................................................................................. 8 3.2 Vattenfall-gebied (zoekgebied wind) ............................................................................................ 9 3.3 Tussen Amsterdam-Rijnkanaal en A1 (zoekgebied -
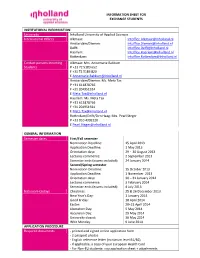
Information Sheet for Exchange Students Institutional Information
INFORMATION SHEET FOR EXCHANGE STUDENTS INSTITUTIONAL INFORMATION University Inholland University of Applied Sciences International Offices Alkmaar: [email protected] Amsterdam/Diemen: [email protected] Delft: [email protected] Haarlem: [email protected] Rotterdam: [email protected] Contact persons Incoming Alkmaar: Mrs. Annemarie Bakkum Students P +31 72 5183 652 F +31 72 5183 820 E [email protected] Amsterdam/Diemen: Ms. Meta Tax P +31 611878766 F +31 204951924 E [email protected] Haarlem: Ms. Meta Tax P +31 611878766 F +31 204951924 E [email protected] Rotterdam/Delft/Den Haag: Mrs. Pearl Steger P +31 010 4392220 E [email protected] GENERAL INFORMATION Semester dates First/Fall semester Nomination Deadline: 15 April 2013 Application Deadline: 1 May 2013 Orientation days: 29 - 30 August 2013 Lectures commence: 2 September 2013 Semester ends (exams included): 24 January 2014 Second/Spring semester Nomination Deadline: 15 October 2013 Application Deadline: 1 November 2013 Orientation days: 30 – 31 January 2014 Lectures commence: 3 February 2014 Semester ends (exams included): 4 July 2013 National Holidays Christmas: 25 & 26 December 2013 New Year’s Day: 1 January 2014 Good Friday: 18 April 2014 Easter: 20+21 April 2014 Liberation Day: 5 May 2014 Ascension Day: 29 May 2014 University closed: 30 May 2014 Whit Monday: 9 June 2014 APPLICATION PROCEDURE Required documents - printed and signed online application form - 2 passport photos - English reference letter (minimum level B1/B2) - if applicable, a copy of your European Health Card - For Non-EU students: visa application sheet + attachments For Non-EU students Please click here to see if you need a visa to enter the Netherlands. -

Megalithic Research in the Netherlands, 1547-1911
J.A. B A KKER Megalithic Research in the Netherlands The impressive megalithic tombs in the northeastern Netherlands are called ‘hunebedden’, meaning ‘Giants’ graves’. These enigmatic Neolithic structures date to around 3000 BC and were built by the Funnelbeaker, or TRB, people. The current interpretation of these monuments, however, is the result of over 400 years of megalithic research, the history of which is recorded in this book. The medieval idea that only giants could have put the huge boulders of which they were made into position was still defended in 1660. Others did not venture to MEG explain how hunebeds could have been constructed, but ascribed them to the most I ancient, normally sized inhabitants. 16th-century writings speculated that Tacitus was N THE NETHE referring to hunebeds when he wrote about the ‘Pillars of Hercules’ in Germania. A Titia Brongersma is the first person recorded to do excavations in a hunebed, in LITHIC RESE 1685. The human bones she excavated were from normally sized men and suggested that such men, not giants, had constructed the hunebeds. Other haphazard diggings followed, but much worse was the invention of stone covered dikes which required large amounts of stone. This launched a widespread collection of erratic boulders, which included the hunebeds. Boundary stones were stolen and several hunebeds R were seriously damaged or they vanished completely. Such actions were forbidden in L an 1734, by one of the earliest laws protecting prehistoric monuments in the world. ar DS From the mid 18th century onwards a variety of eminent but relatively unknown CH researchers studied the hunebeds, including Van Lier (1760), Camper and son (1768- 1808), Westendorp (1815), Lukis and Dryden (1878) and Pleyte (1877-1902). -

Het Dagelijks Bestuur Van Het Waterschap Amstel, Gooi En Vecht
Nr. 2760 13 maart WATERSCHAPSBLAD 2019 Officiële uitgave van het dagelijks bestuur van het Waterschap Amstel, Gooi en Vecht HET DAGELIJKS BESTUUR VAN HET WATERSCHAP AMSTEL, GOOI EN VECHT Dat per 1 januari 1997 het waterschap Amstel, Gooi en Vecht (verder: het waterschap) als nautisch beheerder is aangewezen van alle scheepvaartwegen binnen zijn beheersgebied, behoudens het Amsterdam-Rijnkanaal, de Amstel, de Loosdrechtse - en Vinkeveensche-Plassen, het Hilversums-Kanaal; Dat de gemeente Gooise Meren bij brief van 25 september 2018, met zaaknummer 974575, het waterschap heeft gevraagd om voor de bouw van drie nieuwe bruggen over de Muidertrekvaart tijdelijk de BRTN DM doorvaarthoogte van 2,40 naar 1,50 meter aan te passen; Dat vanaf maart 2019 tot 1 april 2020 drie nieuwe bruggen over de Muidertrekvaart worden gerealiseerd en één oude brug wordt verwijderd; Dat het om (veiligheids-)technische redenen noodzakelijk is dat er ter hoogte van de bouwlocaties, tijdens de uitvoering, een hoogtebeperking wordt ingesteld; Dat er om die reden van 1 maart 2019 tot 1 april 2020 tussen de Penbrug te Diemen en de Amsterdamse - Poortbrug te Muiden een tijdelijk doorvaarthoogte beperking van 1,50 meter moet worden ingesteld; Dat dit besluit plaatsvindt in het belang van het verzekeren van een veilig verloop van het scheepvaartverkeer; Dat het waterschap op grond van artikel 6 van het Besluit administratieve bepalingen scheepvaartverkeer over dit besluit bij brief van 20 november 2018 de BLN/Schuttevaer (18.055639), gemeente Diemen (18.055694), gemeente -

Grens Gemeente Gooise Meren En Weesp
2015 90 Besluit van gedeputeerde staten van Noord-Holland van 30 juni 2015, nr. 305888/610701, tot vaststelling van de grensbeschrijving van de nieuwe gemeente Gooise Meren en de grensbeschrijving van de gemeente Weesp Gedeputeerde Staten van Noord-Holland; gelet op publicatie van de wet tot samenvoeging van de gemeenten Bussum, Muiden en Naarden en wijziging van de grens met de gemeente Weesp in Staatsblad 216, jaargang 2015; gelet op publicatie van het besluit van houdende het tijdstip van inwerkingtreding van deze wet in Staatsblad 217, jaargang 2015; gelet op artikel 2, tweede lid, van de Wet algemene regels herindeling; Besluiten: Artikel 1 Gedeputeerde staten stellen de navolgende beschrijving van de grens vast van de nieuwe gemeente Gooise Meren, die zijn aangegeven op de bij dit besluit behorende twee kaarten: A. Grens met Amsterdam Vanaf het snijpunt van de grens tussen de op te heffen gemeente Muiden en de gemeenten Weesp en Amsterdam volgt de nieuwe grens de huidige grens tussen de op te heffen gemeente Muiden en de gemeente Amsterdam tot aan het snijpunt van de huidige grens van de op te heffen gemeente Muiden en de gemeenten Amsterdam en Diemen. B. Grens met Diemen Vanaf het onder A. laatstgenoemde snijpunt volgt de nieuwe grens de huidige grens tussen de op te heffen gemeente Muiden en de gemeente Diemen tot aan het snijpunt van de huidige grens van de op te heffen gemeente Muiden en de gemeenten Diemen en Amsterdam. C. Grens met Amsterdam Vanaf het onder B laatstgenoemde snijpunt volgt de nieuwe grens de huidige grens tussen de op te heffen gemeente Muiden en de gemeente Amsterdam tot aan het snijpunt van de huidige grens van de op te heffen gemeenten Muiden en Amsterdam en de gemeente Waterland en de gemeente Almere. -

6. RV Regionale Detailhandelsvisie Amstelland-Meerlanden
gemeente Haarlemmermeer raadsvoorstel Onderwerp Regionale detailhandelsvisie Amstelland-Meerlanden Portefeuillehoudersdrs. Marja Ruigrok, Johan Rip Steller Caroline Rindertsma Collegevergadering 1 juni 2021 Raadsvergadering Raadsvoorstelnummer 2021.0001238 1. Voorstel Collegebesluit(en) Het college besluit de raad voor te stellen om: 1. de regionale detailhandelsvisie Amstelland-Meerlanden met ingangsdatum 1 september 2021 vast te stellen met daarin afspraken om te voldoen aan het provinciale detailhandelsbeleid en een leidraad voor regionale samenwerking voor detailhandelsontwikkeling. 2. Samenvatting In het 'Detailhandelsbeleid Noord-Holland 2015-2020' verplicht de provincie Noord-Hollandse regio's om een regionale detailhandelsvisie te hebben. De regionale detailhandelsvisie Amstelland-Meerlanden (AM) is een afsprakenkader voor de gemeenten in de AM-regio en bevat afspraken om te voldoen aan het provinciale detailhandelsbeleid. De regionale detailhandelsvisie is een leidraad voor regionale samenwerking op het gebied van detailhandel. De regionale visie en deze afspraken sluiten aan op de lokale detailhandelsvisies van de zes gemeenten in de AM-regio. Voor Haarlemmermeer is dit het beleid voor commerciële voorzieningen, regels en ruimte (2019.0057889). 3. Uitwerking 3.1 Wat willen we bereiken? In het 'Detailhandelsbeleid Noord-Holland 2015-2020' verplicht de provincie Noord-Hollandse regio's om een regionale detailhandelsvisie te hebben. Het 'Regionaal detailhandelsbeleid Stadsregio Amsterdam 2016-2020' loopt dit jaar af. De Stadsregio Amsterdam bestaat inmiddels niet meer en is opgevolgd door de Metropoolregio Amsterdam (MRA). De MRA bestrijkt een groter gebied. Gezien de reikwijdte van de regionale effecten bij dynamiek in de detailhandelssector en koopstromen is een visie op het niveau van de deelregio Amstelland- Meerlanden (AM-regio) ook passender dan op het niveau van de MRA. -

Uva-DARE (Digital Academic Repository)
UvA-DARE (Digital Academic Repository) Corals through the light : phylogenetics, functional diversity and adaptive strategies of coral-symbiont associations over a large depth range Rodrigues Frade, P. Publication date 2009 Document Version Final published version Link to publication Citation for published version (APA): Rodrigues Frade, P. (2009). Corals through the light : phylogenetics, functional diversity and adaptive strategies of coral-symbiont associations over a large depth range. General rights It is not permitted to download or to forward/distribute the text or part of it without the consent of the author(s) and/or copyright holder(s), other than for strictly personal, individual use, unless the work is under an open content license (like Creative Commons). Disclaimer/Complaints regulations If you believe that digital publication of certain material infringes any of your rights or (privacy) interests, please let the Library know, stating your reasons. In case of a legitimate complaint, the Library will make the material inaccessible and/or remove it from the website. Please Ask the Library: https://uba.uva.nl/en/contact, or a letter to: Library of the University of Amsterdam, Secretariat, Singel 425, 1012 WP Amsterdam, The Netherlands. You will be contacted as soon as possible. UvA-DARE is a service provided by the library of the University of Amsterdam (https://dare.uva.nl) Download date:30 Sep 2021 AC KNOWLEDGE M ENTS Finally here I am, writing this long-waited last bit of my thesis. Surely it is the most difficult part to accomplish as I owe the fact of being here now to the help and contribution of many.