DOCSLIB.ORG

The Effect of Loading, Plantar Ligament Disruption and Surgical

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Effect of Loading, Plantar Ligament Disruption and Surgical The Effect of Loading, Plantar Ligament Disruption and Surgical Repair on Canine Tarsal Bone Kinematics Presented by Christopher John Tan Sydney School of Veterinary Science Faculty of Science, The University of Sydney February 2018 A thesis submitted to fulfil requirements for the degree of Doctor of Philosophy i To my wonderful family i This is to certify that to the best of my knowledge, the content of this thesis is my own work. This thesis has not been submitted for any degree or other purposes. I certify that the intellectual content of this thesis is the product of my own work and that all the assistance received in preparing this thesis and sources have been acknowledged. Signature Name: Christopher John Tan ii Table of contents Statement of originality……………………………………………………………………………………………………………………ii Table of figures……………………………………………………………………………………………………………………………….vii Table of tables………………………………………………………………………………………………………………………………..xiii Table of equations………………………………………………………………………………………………………………………….xvi Abbreviations…………………………………………………………………………………………………………………………………xvii Author Attribution Statement and published works…………………………………………………………………….xviii Summary…………………………………………………………………………………………………………………………………………xix Preface…………………………………………………………………………………………………………………………………………….xx Chapter 1 Introduction ........................................................................................................................... 1 1.1 Overview ....................................................................................................................................... 4 Chapter 2 Literature review .................................................................................................................... 6 Section 2.1: Kinematics ....................................................................................................................... 8 2.1.1 Introduction ........................................................................................................................... 8 2.1.2 Modern techniques in kinematic investigations .................................................................. 11 2.1.3 Presentation and application of kinematic data .................................................................. 22 Section 2.2: Biological springs ........................................................................................................... 24 2.2.1 Introduction ......................................................................................................................... 24 2.2.2 The components of biological springs ................................................................................. 25 2.2.3 The importance of the pes in canine locomotion ................................................................ 30 Section 2.3: Pathological disruption of the canine pes ..................................................................... 36 2.3.1 Stress fractures and remodelling of the bones of the pes ................................................... 37 2.3.2 Ligamentous injuries of the canine pes ............................................................................... 41 Section 2.4: Stabilisation techniques following disruption to the pes ............................................. 46 2.4.1 Repair following fracture ..................................................................................................... 46 2.4.2 Repair following ligamentous injury or degeneration ......................................................... 48 Section 2.5 Purpose .......................................................................................................................... 56 Chapter 3 A computed tomography-based technique for the measurement of canine tarsal bone kinematics ............................................................................................................................................. 57 3.1 Introduction ................................................................................................................................ 59 3.2. Materials and methods .............................................................................................................. 60 iii 3.2.1 Specimens ............................................................................................................................ 60 3.2.2 Image acquisition ................................................................................................................. 60 3.2.3 Segmentation and 3D surface model generation ................................................................ 63 3.2.4 Initial alignment to a global co-ordinate system ................................................................. 63 3.2.5 Calculation of kinematics ..................................................................................................... 64 3.2.6 Statistical analysis ................................................................................................................ 66 3.3. Results ........................................................................................................................................ 67 3.3.1 Measurements of the Lego® brick and calculation of ‘known’ bone motions .................... 67 3.3.2 Influence of scan resolution, thresholding and smoothing on 3D surface model parameters ...................................................................................................................................................... 67 3.3.3 Magnitude of error in calculated kinematics ....................................................................... 67 3.3.4 Influence of scan resolution, thresholding and reconstruction algorithm on kinematic accuracy ........................................................................................................................................ 69 3.4 Discussion .................................................................................................................................... 70 3.5 Conclusions ................................................................................................................................. 74 Chapter 4 Development of an ex vivo limb loading device .................................................................. 75 4.1 Chapter Introduction .................................................................................................................. 76 4.2 Experiment 1: Initial concepts and jig design: phase 1 ............................................................... 78 4.2.1 Introduction ......................................................................................................................... 78 4.2.2 Materials and methods ........................................................................................................ 80 4.2.3 Results .................................................................................................................................. 84 4.2.4 Discussion ............................................................................................................................. 86 4.3 Experiment 2: Jig design phase 2 ................................................................................................ 88 4.3.1 Introduction ......................................................................................................................... 88 4.3.2 Materials and methods ........................................................................................................ 89 4.3.3 Results .................................................................................................................................. 97 4.3.4 Discussion ............................................................................................................................. 98 4.4 Experiment 3: Replicating in vivo joint angles .......................................................................... 107 4.4.1 Introduction ....................................................................................................................... 107 4.4.2 Materials and Methods ...................................................................................................... 107 4.4.3 Results ................................................................................................................................ 111 4.4.4 Discussion ........................................................................................................................... 114 4.5 Experiment 4: Replication of joint forces ................................................................................. 116 4.5.1 Introduction ....................................................................................................................... 116 4.5.2 Materials and Methods ...................................................................................................... 116 4.5.3 Results ................................................................................................................................ 119 iv 4.5.4 Discussion ........................................................................................................................... 120 4. 6 Chapter discussion ................................................................................................................... 123 Chapter 5 : Characterisation of canine tarsal bone kinematics identifies the functional units of the canine foot .........................................................................................................................................
Load more

Recommended publications
  • Effect of Starting Distance on Vertical Ground Reaction
    EFFECT OF STARTING DISTANCE ON VERTICAL GROUND REACTION FORCES IN THE DOG by DAVID BURNETT DULANEY (Under Direction the of Hugh Dookwah) ABSTRACT Kinetic gait analysis is used extensively in both human and veterinary medicine, both to detect pathological gait abnormalities and to quantify the efficacy of surgical and pharmacological protocols. This study evaluates the effect of three different staring distances from the kinetic data collection device (2m, 4m, and 6m) on the peak vertical and associated impulse ground reaction forces generated by the test subjects at a trot. Five dogs weighing between 20 and 30kg were trotted over two force plates at between 1.6 and 2.1 m/s until 5 right first contacts and 5 left first contacts were collected. Data collection was repeated approximately a week apart for a total of 5 collections. Vertical impulse values were found to be significantly different (p<0.05) between 2m and 6m, but neither were different from 4m. Peak vertical force was not found to be significantly effected by distance. INDEX WORDS: Gait analysis, force plate, starting distance, steady state gait, peak vertical force, vertical impulse EFFECT OF STARTING DISTANCE ON VERICAL GROUND REACTION FORCES IN THE DOG by DAVID BURNETT DULANEY B.S., Lander University, 1997 A Thesis Submitted to the Graduate Faculty of The University of Georgia in Partial Fulfillment of the Requirements for the Degree MASTERS OF SCIENCE ATHENS, GEORGIA 2003 © 2003 David Burnett DuLaney All Rights Reserved EFFECT OF STARTING DISTANCE ON VERTICAL GROUND REACTION FORCES IN THE DOG by DAVID BURNETT DULANEY Major Professor: Hugh Doowah Committee: Steven Budsberg Paul T.
    [Show full text]
  • Normal and Abnormal Gaits in Dogs
    Pagina 1 di 12 Normal And Abnormal Gait Chapter 91 David M. Nunamaker, Peter D. Blauner z Methods of Gait Analysis z The Normal Gaits of the Dog z Effects of Conformation on Locomotion z Clinical Examination of the Locomotor System z Neurologic Conditions Associated With Abnormal Gait z Gait Abnormalities Associated With Joint Problems z References Methods of Gait Analysis Normal locomotion of the dog involves proper functioning of every organ system in the body, up to 99% of the skeletal muscles, and most of the bony structures.(1-75) Coordination of these functioning parts represents the poorly understood phenomenon referred to as gait. The veterinary literature is interspersed with only a few reports addressing primarily this system. Although gait relates closely to orthopaedics, it is often not included in orthopaedic training programs or orthopaedic textbooks. The current problem of gait analysis in humans and dogs is the inability of the study of gait to relate significantly to clinical situations. Hundreds of papers are included in the literature describing gait in humans, but up to this point there has been little success in organizing the reams of data into a useful diagnostic or therapeutic regime. Studies on human and animal locomotion commonly involve the measurement and analysis of the following: Temporal characteristics Electromyographic signals Kinematics of limb segments Kinetics of the foot-floor and joint resultants The analyses of the latter two types of measurements require the collection and reduction of voluminous amounts of data, but the lack of a rapid method of processing this data in real time has precluded the use of gait analysis as a routine clinical tool, particularly in animals.
    [Show full text]
  • The Role of Joint Biomechanics in the Development of Tarsocrural Osteochondrosis in Dogs
    FACULTY OF VETERINARY MEDICINE approved by EAEVE The Role of Joint Biomechanics in the Development of Tarsocrural Osteochondrosis in Dogs WALTER BENJAMIN DINGEMANSE Thesis submitted in fulfilment of the requirements for the degree of Doctor of Philosophy (PhD) in Veterinary Sciences, Faculty of Veterinary Medicine, Ghent University 2017 Promoters: Dr. Ingrid Gielen Prof. Dr. Ilse Jonkers Prof. Dr. Bernadette Van Ryssen Prof. Dr. Magdalena Müller-Gerbl Department of Veterinary Medical Imaging and Small Animal Orthopaedics Faculty of Veterinary Medicine Ghent University The Role of Joint Biomechanics in the Development of Osteochondrosis in Dogs Walter Benjamin Dingemanse Vakgroep Medische Beeldvorming van de Huisdieren en Orthopedie van de Kleine Huisdieren Faculteit Diergeneeskunde Universiteit Gent Cover design by Michael Edmond Nico Van Waegevelde © Walter Benjamin Dingemanse 2017. No part of this work may be reproduced or transmitted in any form or by any means without permission from the author. PhD supported by a grant from IWT I MAY NOT HAVE GONE WHERE I INTENDED TO GO BUT I THINK I HAVE ENDED UP WHERE I NEEDED TO BE - DOUGLAS ADAMS - EXAMINATION BOARD Chair: Prof. dr. Hilde de Rooster Faculty of Veterinary Medicine, Ghent University, BE Secretary: Prof. dr. Wim Van den Broeck Faculty of Veterinary Medicine, Ghent University, BE Members: Prof. dr. Robert Colborne Institute of Veterinary, Animal & Biomedical Sciences, Massey University, NZ Dr. Evelien de Bakker Faculty of Veterinary Medicine, Ghent University, BE Dr. Maarten Oosterlinck
    [Show full text]
  • Thesis Kinematic and Kinetic Analysis of Canine Thoracic
    THESIS KINEMATIC AND KINETIC ANALYSIS OF CANINE THORACIC LIMB AMPUTEES AT A TROT Submitted by Sarah Jarvis Graduate Degree Program in Bioengineering In partial fulfillment of the requirements For the Degree of Master of Science Colorado State University Fort Collins, Colorado Fall 2011 Master’s Committee: Advisor: Raoul Reiser Deanna Worley Kevin Haussler ABSTRACT KINEMATIC AND KINETIC ANALYSIS OF CANINE THORACIC LIMB AMPUTEES AT A TROT Most dogs appear to adapt well to the removal of a thoracic limb, but clinically there is a particular subset of dogs that still have problems with gait that seem to be unrelated to age, weight, or breed. The purpose of this study was to objectively characterize biomechanical changes in gait associated with amputation of a thoracic limb. Sixteen amputees and 24 control dogs of various breeds with similar stature and mass greater than 14 kg were recruited and participated in the study. Dogs were trotted across three in-series force platforms as spatial kinematic and ground reaction force data were recorded during the stance phase. Ground reaction forces, impulses, and stance durations were computed as well as stance widths, stride lengths, limb and spinal joint angles. Kinetic results show that thoracic limb amputees have increased stance times and vertical impulses. The remaining thoracic limb and pelvic limb ipsilateral to the side of amputation compensate for the loss of braking, and the ipsilateral pelvic limb also compensates the most for the loss of propulsion. The carpus, and ipsilateral hip and stifle joints are more flexed during stance, and the T1, T13, and L7 joints experience significant differences in spinal motion in both the sagittal and horizontal planes throughout the gait cycle stance phases.
    [Show full text]
  • Use of a Collar-Mounted Triaxial Accelerometer to Predict Speed and Gait in Dogs
    animals Article Use of a Collar-Mounted Triaxial Accelerometer to Predict Speed and Gait in Dogs Samantha Bolton, Nick Cave *, Naomi Cogger and G. R. Colborne School of Veterinary Science, Massey University, Palmerston North 4442, New Zealand; [email protected] (S.B.); [email protected] (N.C.); [email protected] (G.R.C.) * Correspondence: [email protected]; Tel.: +64-6-3505329 Simple Summary: Accelerometers have been used for several years to monitor activity in free- moving dogs. The technique has particular utility for measuring the efficacy of treatments for osteoarthritis when changes to movement need to be monitored over extended periods. While collar- mounted accelerometer measures are precise, they are difficult to express in widely understood terms, such as gait or speed. This study aimed to determine whether measurements from a collar-mounted accelerometer made while a dog was on a treadmill could be converted to an estimate of speed or gait. We found that gait could be separated into two categories—walking and faster than walking (i.e., trot or canter)—but we could not further separate the non-walking gaits. Speed could be estimated but was inaccurate when speed exceeded 3 m/s. We conclude that collar-mounted accelerometers only allowing limited categorisation of activity are still of value for monitoring activity in dogs. Abstract: Accelerometry has been used to measure treatment efficacy in dogs with osteoarthritis, although interpretation is difficult. Simplification of the output into speed or gait categories could simplify interpretation. We aimed to determine whether collar-mounted accelerometry could estimate the speed and categorise dogs’ gait on a treadmill.
    [Show full text]
  • Foot and Ankle Pain
    Foot and Ankle Pain Pain in the ankle and foot may arise from the bones and joints, periarticular soft tissues, nerve roots and peripheral nerves, or vascular structures or referred from the lumbar spine or knee joint. Precise diagnosis of ankle and foot pain rests on a careful history, a thorough examination and a few rationally selected diagnostic tests. The foot can be divided into three sections: hindfoot, midfoot, and forefoot. The hindfoot consists of the calcaneus and talus. The anterior two thirds of the calcaneus articulates with the talus, and the posterior third forms the heel. Medially the sustentaculum tali supports the talus and is joined to the navicular bone by the spring ligament. The talus articulates with the tibia and fibula above at the ankle joint, with the calcaneus below at the subtalar joint, and with the navicular in front at the talonavicular joint. Five tarsal bones make up the midfoot: navicular medially, cuboid laterally and the three cuneiforms distally. The midfoot is separated from the hindfoot by the mid- or transverse tarsal joint (talonavicular and calcaneocuboid articulations), and from the forefoot by the tarsometarsal joints. The forefoot comprises the metatarsals and phalanges. The great toe has two phalanges and two sesamoids embedded in the plantar ligament under the metatarsal head. Each of the other toes has three phalanges. The distal tibiofibular joint is a fibrous joint or syndesmosis between the distal ends of the tibia and fibula. The joint only allows slight malleolar separation on full dorsiflexion of the ankle. Section 21 Page 1 The ankle or talocrural joint is a hinge joint between the distal ends of the tibia and fibula and the trochlea of the talus.
    [Show full text]
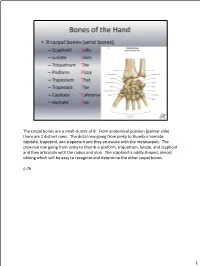
  • The Carpal Bones Are a Small Cluster of 8. from Anatomical Position (Palmar Side) There Are 2 Distinct Rows
    The carpal bones are a small cluster of 8. From anatomical position (palmar side) there are 2 distinct rows. The distal row going from pinky to thumb is hamate, capitate, trapezoid, and trapezium and they articulate with the metacarpals. The proximal row going from pinky to thumb is pisiform, triquetrum, lunate, and scaphoid and they articulate with the radius and ulna. The scaphoid is oddly shaped, almost oblong which will be easy to recognize and determine the other carpal bones. p.76 1 Radiocarpal ligaments (palmar and dorsal)--Connects radius to carpal bones Intercarpal ligaments (palmar and dorsal)--Connects carpal bones to each other Collateral ligaments (ulnar and radial)--Ulnar collateral ligament and radial collateral ligament connect the forearm to the wrist and help support the sides of the wrist as well There are radiocarpal ligaments and intercarpal ligaments on both the dorsal and palmar sides of the hand. p.78 2 So for the middle phalanges there are only #2-5 since the thumb does not have a middle phalange. The proximal phalange and middle phalange articulation is called the proximal interphalangeal joint and the middle phalange articulating with the distal phalange is called the distal interphalangeal joint. With the thumb there is only 1 interphalangeal joint since it’s just the proximal and distal phalange. p.77 3 p.77 4 The radiocarpal joint is where the carpals articulate with the radius (condyloid joint). The intercarpal joints are the gliding joints between the carpals. The 1st carpometacarpal joint is the thumb, which is a saddle joint, but the 2nd-5th carpometacarpal joints are gliding.
    [Show full text]
  • A Three Dimensional Multiplane Kinematic Model for Bilateral Hind Limb Gait Analysis In
    bioRxiv preprint doi: https://doi.org/10.1101/320812; this version posted May 11, 2018. The copyright holder for this preprint (which was not certified by peer review) is the author/funder. This article is a US Government work. It is not subject to copyright under 17 USC 105 and is also made available for use under a CC0 license. 1 A three dimensional multiplane kinematic model for bilateral hind limb gait analysis in 2 cats 3 4 Nathan P. Brown1,2,3, Gina E. Bertocci1,2, Kimberly A. Cheffer2,3,4, Dena R. Howland2,3,5* 5 6 1 Department of Bioengineering, J.B. Speed School of Engineering, University of Louisville, 7 Louisville, Kentucky, United States of America 8 2 Kentucky Spinal Cord Injury Research Center, University of Louisville, Louisville, Kentucky, 9 United States of America 10 3 Research Service, Robley Rex VA Medical Center, Louisville, Kentucky, United States of 11 America 12 4 Department of Anatomical Sciences and Neurobiology, School of Medicine, University of 13 Louisville, Louisville, Kentucky, United States of America 14 5 Department of Neurological Surgery, School of Medicine, University of Louisville, Louisville, 15 Kentucky, United States of America 16 17 *Corresponding author 18 E-mail: [email protected] (DH) 1 bioRxiv preprint doi: https://doi.org/10.1101/320812; this version posted May 11, 2018. The copyright holder for this preprint (which was not certified by peer review) is the author/funder. This article is a US Government work. It is not subject to copyright under 17 USC 105 and is also made available for use under a CC0 license.
    [Show full text]
  • Evaluation of Pacing As an Indicator of Musculoskeletal Pathology in Dogs
    Vol. 8(12), pp. 207-213, December 2016 DOI: 10.5897/JVMAH2016.0512 Article Number: 62D6B3B61551 Journal of Veterinary Medicine and ISSN 2141-2529 Copyright © 2016 Animal Health Author(s) retain the copyright of this article http://www.academicjournals.org/JVMAH Full Length Research Paper Evaluation of pacing as an indicator of musculoskeletal pathology in dogs Theresa M. Wendland, Kyle W. Martin, Colleen G. Duncan, Angela J. Marolf and Felix M. Duerr* Department of Clinical Sciences, Colorado State University, United States. Received 4 August, 2016: Accepted 13 October, 2016 Little is currently known about the pacing gait in dogs and it has been speculated that pacing may be utilized by dogs with musculoskeletal pathology. The goals of the present study were to determine if pacing in dogs is associated with musculoskeletal disease and to establish if controlled speed impacts pacing. Dogs underwent orthopedic and lameness assessments. Musculoskeletal pathology, when identified, was further defined with radiography of the affected area. Dogs were considered musculoskeletally normal (MSN) if no pathology was detected and they had no history of musculoskeletal disease. All others were considered musculoskeletally abnormal (MSA). Animals were then evaluated for pacing using digital-video-imaging under three conditions: Off-lead, lead-controlled, and on a treadmill. Thirty-nine dogs were enrolled (MSN: n = 20; MSA: n = 19). Overall, pacing was observed more frequently in dogs under lead-controlled than off-lead conditions (P < 0.001). Lead- controlled MSN dogs were observed to pace significantly more frequently (n = 17/20) than lead- controlled MSA dogs (n = 10/19; P = 0.029).
    [Show full text]
  • Articulations
    9 Articulations PowerPoint® Lecture Presentations prepared by Jason LaPres Lone Star College—North Harris © 2012 Pearson Education, Inc. 9-1 Classification of Joints • Functional Classifications • Synarthrosis (immovable joint) • Amphiarthrosis (slightly movable joint) • Diarthrosis (freely movable joint) © 2012 Pearson Education, Inc. 9-1 Classification of Joints • Synovial Joints (Diarthroses) • Also called movable joints • At ends of long bones • Within articular capsules • Lined with synovial membrane © 2012 Pearson Education, Inc. 9-2 Synovial Joints • Articular Cartilages • Pad articulating surfaces within articular capsules • Prevent bones from touching • Smooth surfaces lubricated by synovial fluid • Reduce friction © 2012 Pearson Education, Inc. 9-2 Synovial Joints • Synovial Fluid • Contains slippery proteoglycans secreted by fibroblasts • Functions of synovial fluid 1. Lubrication 2. Nutrient distribution 3. Shock absorption © 2012 Pearson Education, Inc. 9-2 Synovial Joints • Accessory Structures • Cartilages • Fat pads • Ligaments • Tendons • Bursae © 2012 Pearson Education, Inc. 9-2 Synovial Joints • Cartilages • Cushion the joint • Fibrocartilage pad called a meniscus (or articular disc; plural, menisci) • Fat Pads • Superficial to the joint capsule • Protect articular cartilages • Ligaments • Support, strengthen joints • Sprain – ligaments with torn collagen fibers © 2012 Pearson Education, Inc. 9-2 Synovial Joints • Tendons • Attach to muscles around joint • Help support joint • Bursae • Singular, bursa, a pouch • Pockets
    [Show full text]
  • Canine Locomotion: Similarities and Differences to Horses M. Christine
    Canine Locomotion: Similarities and Differences to Horses M. Christine Zink, DVM, PhD, DACVP, DACVSMR, CVSMT With increasing numbers of dogs competing in sports competitions, it is critical for veterinarians to thoroughly understand canine locomotion and gait. While equine gait is taught in veterinary school, few curricula include information about canine gait, which has both similarities and differences to horses. Dogs are built very differently from horses and that is reflected in their use of different gaits. In fact, dogs use some gaits that would be considered completely abnormal in horses. There are three structural features that make dogs different from horses: Dogs have a much more flexible spine. Horses have 17 (Arabians) or 18 ribs and a large intestine full of hay in various stages of digestion. As a result they have minimal ability to bend their vertebral column. In contrast, a dog has only 13 ribs and a low-volume intestine. In addition, dogs have a comparatively longer lumbar area (7 lumbar vertebrae as compared to 6 in the horse). Further, horses have joints between the transverse processes of L4 to L6, reducing the flexibility of that part of the spine. Thus the dog is able to flex and extend its spine to a much greater degree than the horse. This produces a great deal of power for forward drive. Picture the image of a greyhound that can be seen on the side of buses. You would never see a horse with its legs extended so far forward and backward. That is the incredible power of the canine spine.
    [Show full text]
  • Gross Anatomy of the Lower Limb. Knee and Ankle Joint. Walking
    Gross anatomy of the lower limb. Knee and ankle joint. Walking. Sándor Katz M.D.,Ph.D. Knee joint type: trochoginglimus (hinge and pivot) Intracapsular ligaments: • Anterior cruciate lig. • Posterior cruciate lig. • Transverse lig. • Posterior meniscofemoral .lig. Medial meniscus: C- shaped. Lateral meniscus: almost a complete ring. Knee joint Extracapsular ligaments. Tibial collateral lig. is broader and fuses with the articular capsule and medial meniscus. Fibular collateral lig. is cord-like and separates from the articular capsule. Knee joint - extracapsular ligaments Knee joint - bursae Knee joint - movements • Flexion: 120-130° • Hyperextension: 5° • Voluntary rotation: 50-60° • Terminal rotation: 10° Ankle (talocrural) joint type: hinge Talocrural joint - medial collateral ligament Medial collateral = deltoid ligament Tibionavicular part (1) (partly covers the anterior tibiotalar part) Tibiocalcaneal part (2-3) Posterior tibiotalar part (4) Medial process (6) Sustentaculum tali (7) Tendon of tibialis posterior muscles (9) Talocrural joint - lateral collateral ligament Lateral collateral ligament Anterior talofibular ligament (5, 6) Calcaneofibular ligament (10) Lateral malleolus (1) Tibia (2) Syndesmosis tibiofibularis (3, 4) Talus (7) Collum tali (8) Caput tali (9) Interosseous talocalcaneal ligament (11) Cervical ligament (12) Talonavicular ligament (13) Navicular bone (14) Lateral collateral ligament Posterior talofibular ligament (5) Fibula (1) Tibia (2) Proc. tali, tuberculum laterale (3) Proc. tali, tuberculum mediale (11) Tendo, musculus felxor hallucis longus (8) Lig. calcaneofibulare (12) Tendo, musculus peroneus brevis (13) Tendo, musculus peroneus longus (14) Art. subtalaris (15) Talocrural joint - movements Dorsiflexion: 15° Plantarfelxion: 40° Talotarsal joint (lower ankle joint): talocalcaneonavicular joint and subtalar joint Bony surfaces: anterior and middle talar articular surfaces and head of the talus + anterior and middle calcaneal articular surfaces, navicular.
    [Show full text]