DOCSLIB.ORG

Downloads:3127

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Downloads:3127 Flat Jack Method for Measuring Design Parameters for Hydraulic Structures of the Koyna Hydro Electric Project in India Keshav Ral Dhawan, Chief Research Officer, Central Water & Power Research Station, Khadakwasla, Pune– 411 024; [email protected] ABSTRACT: The paper presents two different projects: The first involves a case with limited rock cover on a side of an excavated surge shaft located near a steep slope. The second involves the assessment of design parameters of an existing masonry dam for use as input in dynamic analysis. The induced stresses in the surge shaft of Koyna Hydro Electric Project (K.H.E.P.) stage-IV were measured with flat jack. These tests were first performed in a 4 m diameter pilot shaft and after the shaft was excavated to its full diameter of 22.70 m. The stresses increased from 3.96 MPa to 5.09 MPa, when the 4m- diameter surge shaft was expanded to its full diameter of 22.70 m, in the case where significant rock mass cover existed at EL 651.00 m. However stress reduction or no variation in the induced stress was measured in the portion of insufficient rock cover. In the second case, to determine the design parameters of Kolkewadi masonry dam of K.H.E.P stage-III, flat jack tests were conducted at the upstream side of Kolkewadi masonry dam in masonry of 1:4 and 1:3 and at downstream sloping side in masonry of 1:5. It is impractical and difficult to obtain mechanical properties of masonry in laboratory from the extracted core samples, due to intrinsic nonhomogeneity of the material. The brick/stone and mortar layers caused anisotropic behavior of masonry. Average deformation modulus for 1:3 masonry was 32.8 GPa. Similarly, the average deformation modulus for the 1:4 and 1:5 masonry was 19.0 and 13.7 GPa respectively and were adopted for the dynamic analysis. Induced stresses in the masonry dam were found to be nearly equal to the overburden. KEYWORDS: flat jack, masonry dam, surge shaft, deformation modulus, induced stresses SITE LOCATION: IJGCH-database.kmz INTRODUCTION The surge shaft is an important component of the Koyna Hydro Electric Project (K. H. E. P), Stage-IV. Fig.1 shows the location of different stages of the K. H. E. P. The surge shaft is located in a narrow hill with low rock cover i.e. less than 4 times the surge shaft diameter. The lower rock cover is present around North-East-South (N-E-S) side of the surge shaft due to very complex topography. Fig.2 shows the location of the surge shaft in the hill slope. The effect of lower rock cover was required to be investigated (Dhawan and Singh, 2002). The rock cover effect was investigated around the 121 m deep; 22.70 m diameter surge shaft of K. H. E. P, Stage-IV, by flat jack tests around the surge shaft (Fig.3). The local geology indicates presence of alternate layers of volcanic breccia and amygdaloidal basalt. Volcanic breccia is located between EL 682 to 692 m, 647 to 655 m and 610 to 619 m and the rest comprises of amygdaloidal basalt. As the upsurge in the surge shaft may reach up to EL 651.00 m, in-situ studies to determine the stresses near that level were required to be carried out. To determine the induced stresses and effect of lower rock cover, flat jack tests were conducted at two elevations: at EL 637.60 m in basalt and 651.0 m in volcanic breccia in the 4 m diameter pilot shaft (Fig.3) and at EL 651.0 m in the fully expanded surge shaft of 22.70 m diameter. Another application of flat jack test is presented for the Kolkewadi uncoursed rubble (UCR) masonry dam located at Alore village, District Chiplun, Maharashtra and part of K.H.E.P. Fig.1 shows the location of Kolkewadi dam which is Stage-III of K.H.E.P. The length and height of Kolkewadi dam is 497.0m and 56.80m with gross storage of 36.22 Mm3.The dam was constructed in 1975, when the seismic activity was considered low in Koyna region. The Government of Maharashtra formed an Experts’ Committee after the Killari earthquake (magnitude 6.4 Richter scale) on 30th September 1993 near the Submitted: 11 March 2011; Published: 21 May 2012 Reference: Dhawan, K.R. (2012). Flat Jack Method for Measuring Design Parameters for Hydraulic Structures of the Koyna Hydro Electric Project in India. International Journal of Geoengineering Case histories, http://casehistories.geoengineer.org, Vol.2, Issue 3, p.182-195. doi: 10.4417/IJGCH-02-03-01 International Journal of Geoengineering Case Histories ©, Vol. 2, Issue 3, p. 182 http://casehistories.geoengineer.org dam. The Committee recommended carrying out dynamic analysis of Kolkewadi dam by adopting realistic design parameters for the different parts of the dam. These parameters needed to be determined. Major portions of the dam have been constructed with UCR masonry with different proportions of cement sand to mortar ratios of 1:3, 1:4, and 1:5. Cores of different sizes (100 and 150 mm diameter) were extracted from masonry parts of the dam body and were tested in the laboratory to assess the design parameters. Laboratory test results of masonry cores indicated large variation of properties due to variations in percentage of mortar, as well as orientation and size of stones in the extracted cores. Thus, in-situ testing of the masonry portion of the dam was required to be conducted using the flat jack method in an effort to assess the deformation modulus, Poisson’s ratio and induced stresses. The technology of the flat jack test has been modified and adopted for the purpose of evaluation of brick and stone masonry structures in Italy by Rossi (1982, 1985). Rossi developed initial specifications for the optimum size and placement of flat jacks, techniques for measuring deformations, the proper calibration of flat jacks, and post-test analysis of data. Analytical studies have been performed in support of the experimental results. Sachhi et al. (1986) conducted extensive nonlinear finite element analyses of both the single and double flat jack tests in masonry materials. They found their numerical models to be generally in support of experimental evidence, and offered some insight regarding the effect of certain assumptions on the accuracy of the results. Based on their analytical work, the authors recommend that if the flat jack test is carried out to failure on masonry, the failure stress should be reduced by 20% to estimate the unrestrained compressive strength. Similarly, the in-situ stress test may overestimate the actual state of stress by as much as 10% according to their models. It is explained that the Flat jack test provides a direct measure of the vertical stress at a point in the structure. Thus, the test provides an indication of the factor of safety in terms of compression failure in masonry. The test also yields deformation modulus and Poison’s ratio of the tested material. Figure 1. Koyna H.E. Project (Stage I-II-III-IV) schematic layout. CASE STUDY I: IN-SITU STRESSES IN ROCK MASS AT SURGE SHAFT OF KOYNA H.E. PROJECT In order to account for the lower rock cover available around the surge shaft, flat jack studies were performed to measure the induced stresses and deformability of the rock mass in the surge shaft at two stages of excavation (Dhawan and Singh, 2004). At the first stage the measurements were carried out in the 4 m diameter pilot shaft at two levels: at EL 637.60 m in amygdaloidal basalt and at EL. 651.0 m in breccia (Fig. 4), to allow for a comparison of the state of stress and deformability at these levels. In the second stage, measurements of induced stresses and deformability of the rock mass were made for the fully excavated surge shaft of 22.70 m diameter at EL. 651.0 m only (Fig.4), as adequate rock cover was available at EL. 637.00 m. The flat jack test locations are shown in Fig.4. International Journal of Geoengineering Case Histories ©, Vol. 2, Issue 3, p. 183 http://casehistories.geoengineer.org Figure 2. Schematic layout of Koyna H.E.Project stage-IV. Figure 3. Location of flat jack test platforms in pilot shaft and other major constituents of the surge shaft. International Journal of Geoengineering Case Histories ©, Vol. 2, Issue 3, p. 184 http://casehistories.geoengineer.org Figure 4. Location of flat Jack tests at EL 637.60 m. and 651.0 m. in pilot shaft and at EL 651.0 m. in fully excavated shaft (radii not in scale) Evaluation of In-situ Stresses When stresses are to be determined near the surface, as in this case, the flat jack method represents probably the most suitable method. The flat jack tests were carried out in the surge shaft, as per I.S.13946, Part IV, (1994). Equation 1 is used to evaluate the stresses: PK1=PθK2+Ph K3 (1) Where P is the cancellation pressure, P and Ph are the yielding stress in the horizontal and vertical slot directions respectively (Owen and Hinton, 1980). Constants K1, K2, K3 are determined to account for the size of slot effects, expressed by equations 2, 3 and 4: Y 1 (2) KC1 o 1 ao Co ao 1 Y K C Yo a C1 2 Yo (3) 2 a C Y 1 (4) K3 Yo 2 a C a where: Y 2 Y 2 a and a o 1 2 1 2 Co C The length of flat jack is 2Co, Poisson’s ratio,, length of slot is 2C, distance between two reference pins is 2Y and width of slot is 2Yo.The slot axis is passing through the center of slot section and parallel to the plane of slot width (Fig.5).
Load more

Recommended publications
  • Dams-In-India-Cover.Pdf
    List of Dams in India List of Dams in India ANDHRA PRADESH Nizam Sagar Dam Manjira Somasila Dam Pennar Srisailam Dam Krishna Singur Dam Manjira Ramagundam Dam Godavari Dummaguden Dam Godavari ARUNACHAL PRADESH Nagi Dam Nagi BIHAR Nagi Dam Nagi CHHATTISGARH Minimata (Hasdeo) Bango Dam Hasdeo GUJARAT Ukai Dam Tapti Dharoi Sabarmati river Kadana Mahi Dantiwada West Banas River HIMACHAL PRADESH Pandoh Beas Bhakra Nangal Sutlej Nathpa Jhakri Dam Sutlej Chamera Dam Ravi Pong Dam Beas https://www.bankexamstoday.com/ Page 1 List of Dams in India J & K Bagihar Dam Chenab Dumkhar Dam Indus Uri Dam Jhelam Pakal Dul Dam Marusudar JHARKHAND Maithon Dam Maithon Chandil Dam Subarnarekha River Konar Dam Konar Panchet Dam Damodar Tenughat Dam Damodar Tilaiya Dam Barakar River KARNATAKA Linganamakki Dam Sharavathi river Kadra Dam Kalinadi River Supa Dam Kalinadi Krishna Raja Sagara Dam Kaveri Harangi Dam Harangi Narayanpur Dam Krishna River Kodasalli Dam Kali River Basava Sagara Krishna River Tunga Bhadra Dam Tungabhadra River, Alamatti Dam Krishna River KERALA Malampuzha Dam Malampuzha River Peechi Dam Manali River Idukki Dam Periyar River Kundala Dam Parambikulam Dam Parambikulam River Walayar Dam Walayar River https://www.bankexamstoday.com/ Page 2 List of Dams in India Mullaperiyar Dam Periyar River Neyyar Dam Neyyar River MADHYA PRADESH Rajghat Dam Betwa River Barna Dam Barna River Bargi Dam Narmada River Bansagar Dam Sone River Gandhi Sagar Dam Chambal River . Indira Sagar Narmada River MAHARASHTRA Yeldari Dam Purna river Ujjani Dam Bhima River Mulshi
    [Show full text]
  • Annexure-V State/Circle Wise List of Post Offices Modernised/Upgraded
    State/Circle wise list of Post Offices modernised/upgraded for Automatic Teller Machine (ATM) Annexure-V Sl No. State/UT Circle Office Regional Office Divisional Office Name of Operational Post Office ATMs Pin 1 Andhra Pradesh ANDHRA PRADESH VIJAYAWADA PRAKASAM Addanki SO 523201 2 Andhra Pradesh ANDHRA PRADESH KURNOOL KURNOOL Adoni H.O 518301 3 Andhra Pradesh ANDHRA PRADESH VISAKHAPATNAM AMALAPURAM Amalapuram H.O 533201 4 Andhra Pradesh ANDHRA PRADESH KURNOOL ANANTAPUR Anantapur H.O 515001 5 Andhra Pradesh ANDHRA PRADESH Vijayawada Machilipatnam Avanigadda H.O 521121 6 Andhra Pradesh ANDHRA PRADESH VIJAYAWADA TENALI Bapatla H.O 522101 7 Andhra Pradesh ANDHRA PRADESH Vijayawada Bhimavaram Bhimavaram H.O 534201 8 Andhra Pradesh ANDHRA PRADESH VIJAYAWADA VIJAYAWADA Buckinghampet H.O 520002 9 Andhra Pradesh ANDHRA PRADESH KURNOOL TIRUPATI Chandragiri H.O 517101 10 Andhra Pradesh ANDHRA PRADESH Vijayawada Prakasam Chirala H.O 523155 11 Andhra Pradesh ANDHRA PRADESH KURNOOL CHITTOOR Chittoor H.O 517001 12 Andhra Pradesh ANDHRA PRADESH KURNOOL CUDDAPAH Cuddapah H.O 516001 13 Andhra Pradesh ANDHRA PRADESH VISAKHAPATNAM VISAKHAPATNAM Dabagardens S.O 530020 14 Andhra Pradesh ANDHRA PRADESH KURNOOL HINDUPUR Dharmavaram H.O 515671 15 Andhra Pradesh ANDHRA PRADESH VIJAYAWADA ELURU Eluru H.O 534001 16 Andhra Pradesh ANDHRA PRADESH Vijayawada Gudivada Gudivada H.O 521301 17 Andhra Pradesh ANDHRA PRADESH Vijayawada Gudur Gudur H.O 524101 18 Andhra Pradesh ANDHRA PRADESH KURNOOL ANANTAPUR Guntakal H.O 515801 19 Andhra Pradesh ANDHRA PRADESH VIJAYAWADA
    [Show full text]
  • Indian Society of Engineering Geology
    Indian Society of Engineering Geology Indian National Group of International Association of Engineering Geology and the Environment www.isegindia.org List of all Titles of Papers, Abstracts, Speeches, etc. (Published since the Society’s inception in 1965) November 2012 NOIDA Inaugural Edition (All Publications till November 2012) November 2012 For Reprints, write to: [email protected] (Handling Charges may apply) Compiled and Published By: Yogendra Deva Secretary, ISEG With assistance from: Dr Sushant Paikarai, Former Geologist, GSI Mugdha Patwardhan, ICCS Ltd. Ravi Kumar, ICCS Ltd. CONTENTS S.No. Theme Journal of ISEG Proceedings Engineering Special 4th IAEG Geology Publication Congress Page No. 1. Buildings 1 46 - 2. Construction Material 1 46 72 3. Dams 3 46 72 4. Drilling 9 52 73 5. Geophysics 9 52 73 6. Landslide 10 53 73 7. Mapping/ Logging 15 56 74 8. Miscellaneous 16 57 75 9. Powerhouse 28 64 85 10. Seismicity 30 66 85 11. Slopes 31 68 87 12. Speech/ Address 34 68 - 13. Testing 35 69 87 14. Tunnel 37 69 88 15. Underground Space 41 - - 16. Water Resources 42 71 - Notes: 1. Paper Titles under Themes have been arranged by Paper ID. 2. Search for Paper by Project Name, Author, Location, etc. is possible using standard PDF tools (Visit www.isegindia.org for PDF version). Journal of Engineering Geology BUILDINGS S.No.1/ Paper ID.JEGN.1: “Excessive settlement of a building founded on piles on a River bank”. ISEG Jour. Engg. Geol. Vol.1, No.1, Year 1966. Author(s): Brahma, S.P. S.No.2/ Paper ID.JEGN.209: “Geotechnical and ecologial parameters in the selection of buildings sites in hilly region”.
    [Show full text]
  • Shivajirao Jondhale College Ofengineering (Dombivali)
    Shivajirao Jondhale College OfEngineering (Dombivali) BE Mechanical VII Semester Power Plant Engineering Case Study title: Hydroelectric Power Generation Group members: Name Roll No. 1. Nishikant V. Kulkarni 25 2. Rahul A. Mane 30 What is hydroelectric power generation? Hydroelectric power generation is the term referring to generation of electricityby hydropower i.e. the production of electrical power through the use of the gravitational force of falling or flowing water.Most hydroelectric stations use either the natural drop of a river, such as a waterfall or rapids, or a dam is built across a river to raise the water level, and provide the drop needed to create a driving force. It is the most widely used form of renewable energy, accounting for 16 percent of global electricity generation – 3,427 terawatt-hours of electricity production in 2010 and is expected to increase about 3.1% each year for the next 25 years. Hydropower is produced in 150 countries, with the Asia-Pacific region generating 32 percent of global hydropower in 2010. China is the largest hydroelectricity producer, with 721 terawatt-hours of production in 2010, representing around 17 percent of domestic electricity use. History of hydroelectric power generation: Hydropower has been used since ancient times to grind flour and perform other tasks. In 1878 the world's first hydroelectric power scheme was developed at Cragside in Northumberland, England by William George Armstrong. It was used to power a single arc lamp in his art gallery. The old Schoelkopf Power Station No. 1 near Niagara Falls in the U.S. side began to produce electricity in 1881.
    [Show full text]
  • An Innovative Technique As Lake Tapping for Dam Structure: a Case Study
    International Journal on Recent and Innovation Trends in Computing and Communication ISSN: 2321-8169 Volume: 4 Issue: 4 498 - 501 ______________________________________________________________________________________________ An Innovative Technique as Lake Tapping for Dam Structure: A Case Study Prof. Aakash Suresh Pawar Prof. Lomesh S. Mahajan Prof. Mahesh N. Patil Department of Civil Engineering Department of Civil Engineering Department of Civil Engineering North Maharashtra University, Jalgaon North Maharashtra University, Jalgaon North Maharashtra University, Jalgaon Maharashtra, India Maharashtra, India Maharashtra, India [email protected] [email protected] [email protected] Abstract – From the last three decades water resource management becomes very special issue due to uncertain pattern of rainfall all over globe and mainly its drastically affects in south Asian parts. Hydroelectricity uses the energy of running water, without minimizing its quantity, to generate electricity. Therefore, all hydroelectric developments, of small or huge size, whether run of the river accumulated storage, fit the concept of renewable energy. Hydroelectric power plants reservoirs offer incomparable operational flexibility, since they can fast respond to fluctuations in the demand for electricity. The free to adjustment, flexibility and storage capacity of hydroelectric power plants becomes efficient and considerably economical in supplement the use of irregular sources of renewable energy. The operation of electricity systems depends on rapid and flexible generation sources to meet peak demands, maintain the system voltage levels, and quickly re-establish supply after a blackout. Energy generated by hydroelectric installations can be injected into the electricity system faster than that of any other energy source. So providing ancillary services to the electricity system, thus maintaining the balance of water supply availability and fulfill that demand by using a new technique as an additional arrangement for continuous power generation via lake tapping.
    [Show full text]
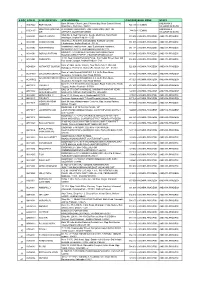
  • S No Atm Id Atm Location Atm Address Pincode Bank
    S NO ATM ID ATM LOCATION ATM ADDRESS PINCODE BANK ZONE STATE Bank Of India, Church Lane, Phoenix Bay, Near Carmel School, ANDAMAN & ACE9022 PORT BLAIR 744 101 CHENNAI 1 Ward No.6, Port Blair - 744101 NICOBAR ISLANDS DOLYGUNJ,PORTBL ATR ROAD, PHARGOAN, DOLYGUNJ POST,OPP TO ANDAMAN & CCE8137 744103 CHENNAI 2 AIR AIRPORT, SOUTH ANDAMAN NICOBAR ISLANDS Shop No :2, Near Sai Xerox, Beside Medinova, Rajiv Road, AAX8001 ANANTHAPURA 515 001 ANDHRA PRADESH ANDHRA PRADESH 3 Anathapur, Andhra Pradesh - 5155 Shop No 2, Ammanna Setty Building, Kothavur Junction, ACV8001 CHODAVARAM 531 036 ANDHRA PRADESH ANDHRA PRADESH 4 Chodavaram, Andhra Pradesh - 53136 kiranashop 5 road junction ,opp. Sudarshana mandiram, ACV8002 NARSIPATNAM 531 116 ANDHRA PRADESH ANDHRA PRADESH 5 Narsipatnam 531116 visakhapatnam (dist)-531116 DO.NO 11-183,GOPALA PATNAM, MAIN ROAD NEAR ACV8003 GOPALA PATNAM 530 047 ANDHRA PRADESH ANDHRA PRADESH 6 NOOKALAMMA TEMPLE, VISAKHAPATNAM-530047 4-493, Near Bharat Petroliam Pump, Koti Reddy Street, Near Old ACY8001 CUDDAPPA 516 001 ANDHRA PRADESH ANDHRA PRADESH 7 Bus stand Cudappa, Andhra Pradesh- 5161 Bank of India, Guntur Branch, Door No.5-25-521, Main Rd, AGN9001 KOTHAPET GUNTUR 522 001 ANDHRA PRADESH ANDHRA PRADESH Kothapeta, P.B.No.66, Guntur (P), Dist.Guntur, AP - 522001. 8 Bank of India Branch,DOOR NO. 9-8-64,Sri Ram Nivas, AGW8001 GAJUWAKA BRANCH 530 026 ANDHRA PRADESH ANDHRA PRADESH 9 Gajuwaka, Anakapalle Main Road-530026 GAJUWAKA BRANCH Bank of India Branch,DOOR NO. 9-8-64,Sri Ram Nivas, AGW9002 530 026 ANDHRA PRADESH ANDHRA PRADESH
    [Show full text]
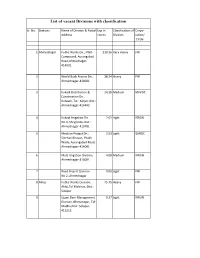
  • List of Vacant Divisions with Classification
    List of vacant Divisions with classification Sr. No. Stations Name of Division & Postal Exp in Classification of Corpo- Address crores Division ration/ Circle 1 Ahmednagar Public Works Dn., PWD 210.36 Very Heavy PW Compound, Aurangabad Road,Ahmednagar- 414001 2 World Bank Project Dn., 38.24 Heavy PW Ahmednagar-414001 3 Kukadi Distribution & 24.38 Medium MKVDC Construction Dn., Kolwadi, Tal : Karjat, Dist : Ahmednagar-414402 4 Kukadi Irrigation Dn. 2.61 Light IRRGN No.II, Shrigonda, Dist : Ahmednagar-413701 5 Medium Project Dn., 2.53 Light GMIDC Sinchan Bhavan, Phakir Wada, Aurangabad Road, Ahmednagar-414001 6 Mula Irrigation Division, 4.08 Medium IRRGN Ahmednagar-414001 7 Road Project Division 0.06 Light PW No.2, Ahmednagar 8 Akluj Public Works Division, 75.75 Heavy PW Akluj,Tal-Malsirus, Dist : Solapur 9 Ujjani Dam Management 0.37 Light IRRGN Division, Bhimanagar, Tal- Madha,Dist : Solapur- 413212 10 Chiplun Irrigation Project 33.25 Medium KIDC Construction Division,Kapsal Vasahat, Chiplun,Dist-Ratnagiri- 415605. 11 Mechanical Dn. for 12.69 Medium IRRGN Konkan Region, Alore, Tal : Chiplun, Dist : Ratnagiri- 415603 12 Construction Dn. (E&M) 6.93 Medium IRRGN No. I, Alore, Tal : Chiplun, Dist : Ratnagiri-415603 13 Quality Control Division, 0.64 Light IRRGN Alore, Chiplun,Dist- Ratnagiri -415603 14 Dhule Sulwade Jamphal Kanoli 136.98 Heavy GMIDC Lift Irrigation Division,Nakane Resorvior Colony,Sakri Road, Dhule- 424002 15 Dhule Medium Project 41.42 Heavy TIDC Dn. ,Sinchan Bhavan, Sakri Road, Dhule-424001 16 Dhule Irrigation Dn., 1.71 Light IRRGN Sinchan Bhavan,Sakri Road, Dhule-424001 17 Quality Control Dn., 0.12 Light IRRGN Sinchan Bhavan, Sakri Road, Dhule-424002 18 Dhule Electrical 0 Light PW Division,Dhule.
    [Show full text]
  • Types of Banks in India and Their Functions
    IBPS PO 2014 BANKING AWARENESS NOTES Bank Rate : 9.0% Repo Rate : 8.0% Reverse Repo Rate : 7.0% Marginal Standing Facility Rate : 9.0% CRR : 4% SLR : 22% Base Rate : 10.00% - 10.25% Savings Deposit Rate : 4.00% Term Deposit Rate : 8.00% - 9.05% 91 day T-bills : 8.5201 % 182 day T-bills : 8.6613% 364 day T-bills : 8.6485 % 364 day T-bills : 8.6485 % Call Rates : 4.00% - 8.70% (ONE BANK FROM ANOTHER BANK) AS ON 02ND OCT.2014 Types of Banks in India and their functions Reserve Bank of India: RBI is the Central Bank of India, which acts as a banker to the government It is also called as ―Bankers bank‖, because all banks will have accounts with RBI. It provides funds to all banks hence it is called as BANKERS BANK RBI was established by an act of Parliament in 1934 It has four zonal offices at Mumbai, Kolkata, Chennai and Delhi and 19 regional offices Current Governor: Dr. Raghuram Rajan Deputy Governors: H R Khan, Dr Urjit Patel, R Gandhi and S S Mundra Head office: Mumbai Functions: Issues currency notes Acts as bankers bank Maintain foreign exchange reserves Maintains CRR and SLR Its affairs are regulated by 21-member central board of directors: Governor (Dr. Raghuram Rajan), 4 deputy Governors, 2 Finance Ministry representatives, 10 Government-nominates directors,4 directors to represent local boards Scheduled Commercial Banks: Scheduled Commercial banks are State Bank of India and its associates (State bank of India has got 7 subsidiaries they are State bank of Hyderabad, State bank of Mysore, State bank of Travancore, State bank of Indore,
    [Show full text]
  • Major Dams in India
    Major Dams in India 1. Bhavani Sagar dam – Tamil Nadu It came into being in 1955 and is built on the Bhavani River. This is the largest earthen dam in India and South Asia and the second-largest in the world. It is in Sathyamangalam district of Tamil Nadu and comes under the Tamil Nadu government. It is 130 ft tall and 8.4 km long with a capacity of 8 megawatts. 2. Tehri Dam – Uttarakhand It is the highest dam in India and comes under the top 10 highest dams in the world. This came into being in 2006 and stands tall on the Bhagirathi river. It is in the Tehri district of Uttarakhand and comes under National Thermal Power Corporation Limited. It is an embankment dam with a height of 855 ft and a length of 1,886 ft. 3. Hirakud dam – Odisha It came into being in 1957 and stands tall on the Mahanadi river. It is one of the first major multipurpose river valley projects in India. This is a composite dam and reservoir and is in the city of Sambalpur in Odisha. It comes under the government of Odisha. It is 200 ft tall and 55 km long and is the longest Dam in India. 4. Bhakra Nangal Dam – Himachal Pradesh It came into being in 1963 and stands tall on the Sutlej river. This is the third-largest reservoir in India and is in Bilaspur district of Himachal Pradesh. It is a concrete gravity dam and comes under the state government of Himachal Pradesh.
    [Show full text]
  • Widening and Strengthening of Existing Pophali -Kondaphansvane Bridge To
    Government of Maharashtra Water Resources Department CHIEF ENGINEER (CIVIL), HYDRO PROJECTS, PUNE BID CAPACITY DOCUMENTS FOR WIDENING AND STRENGTHENING OF EXISTING POPHALI -KONDAPHANSVANE BRIDGE TO SINGLE LANE FOR VEHICULAR TRAFFIC TAL - CHIPLUN DIST - RATNAGIRI Estimate cost put to tender Rs - 2,03,25,044/- KOYNA CONSTRUCTION CIRCLE, SATARA Executive Engineer Kolkewadi Dam Maintenance Division, Alore Tal-Chiplun, Dist, Ratnagiri PIN : 415603 YEAR - 2013-2014 1 Name of Work : - Widening and strengthening of existing Pophali – kondaphansvane Bridge to single lane for vehicular traffic. Class of Registration of the Bidder : Class- III & Above. Limit of tendering : Rs. 203.25 Lakhs . Validity period of registration : Issued to ____________________________________________________________ ____________________________________________________________ D.R. No. : DATE:- Sr.No: Divisional Accounts Officer (Gr-I) Kolkewadi Dam Maintenance Division, Alore, Taluka:- Chiplun, Dist. Ratnagiri CONTRACTOR NO OF CORECTION DY ENGR. EXE.ENGR. 2 INDEX Name of Work:- Widening and strengthening of existing Pophali – kondaphansvane Bridge to single lane for vehicular traffic. , Page No Sr.No. Particulars From To 1.0 SECTION -1 INFORMATION AND INSTRUCTION TO 4 4 APPLICANTS 1.1 General 5 5 1.2 Definition 5 6 1.3 Final Decision Making Authority 6 6 1.4 Clarification 6 6 1.5 Particulars Provisional 6 6 1.6 Site Visit 6 6 1.7 Minimum Eligibility Criteria for bid-capacity 6 7 1.8 Evaluation criteria for bid-capacity 7 8 ANNEX-A 1.9 A. Description of the project 9 9 B. Status of the project 9 9 C. Climatic condition 9 9 D. Scope of the work 9 9 E.1. Details of the work 9 10 2.
    [Show full text]
  • List of Dams and Reservoirs in India 1 List of Dams and Reservoirs in India
    List of dams and reservoirs in India 1 List of dams and reservoirs in India This page shows the state-wise list of dams and reservoirs in India.[1] It also includes lakes. Nearly 3200 major / medium dams and barrages are constructed in India by the year 2012.[2] This list is incomplete. Andaman and Nicobar • Dhanikhari • Kalpong Andhra Pradesh • Dowleswaram Barrage on the Godavari River in the East Godavari district Map of the major rivers, lakes and reservoirs in • Penna Reservoir on the Penna River in Nellore Dist India • Joorala Reservoir on the Krishna River in Mahbubnagar district[3] • Nagarjuna Sagar Dam on the Krishna River in the Nalgonda and Guntur district • Osman Sagar Reservoir on the Musi River in Hyderabad • Nizam Sagar Reservoir on the Manjira River in the Nizamabad district • Prakasham Barrage on the Krishna River • Sriram Sagar Reservoir on the Godavari River between Adilabad and Nizamabad districts • Srisailam Dam on the Krishna River in Kurnool district • Rajolibanda Dam • Telugu Ganga • Polavaram Project on Godavari River • Koil Sagar, a Dam in Mahbubnagar district on Godavari river • Lower Manair Reservoir on the canal of Sriram Sagar Project (SRSP) in Karimnagar district • Himayath Sagar, reservoir in Hyderabad • Dindi Reservoir • Somasila in Mahbubnagar district • Kandaleru Dam • Gandipalem Reservoir • Tatipudi Reservoir • Icchampally Project on the river Godavari and an inter state project Andhra pradesh, Maharastra, Chattisghad • Pulichintala on the river Krishna in Nalgonda district • Ellammpalli • Singur Dam
    [Show full text]
  • Ga Booster Capsule – 2019
    GA BOOSTER CAPSULE – 2019 GA BOOSTER CAPSULE – 2019 Table of Contents 1. Banks in NEWS ............................................................................................................................................. 4 2. Digital Initiatives by Banks .......................................................................................................................... 11 3. Mergers in Indian Banking Industry ............................................................................................................. 12 4. Indian Currency Notes ................................................................................................................................ 14 5. Currency Printing & Coin Minting in India.................................................................................................... 15 6. Types of Banking......................................................................................................................................... 16 7. Digital Banking ............................................................................................................................................ 18 9. Monetary Policies ....................................................................................................................................... 20 10. Important Acts ......................................................................................................................................... 21 11. Important Financial Institutions ..............................................................................................................
    [Show full text]