DOCSLIB.ORG

Göttinger Straßennamen

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

Gerd Tamke / Rainer Driever Göttinger Straßennamen Stadt Göttingen 2012 zum Inhaltsverzeichnis Gerd Tamke / Rainer Driever Göttinger Straßennamen (Veröffentlichung des Stadtarchivs Göttingen 2) herausgegeben von der Stadt Göttingen - Der Oberbürgermeister- Stadtarchiv 3. neu überarbeitete, wesentlich erweiterte Auflage, Göttingen 2012 Gesetzlicher Hinweis Mit Urteil vom 12. Mai 1998 hat das Landgericht Hamburg entschieden, dass der Betreiber einer Internetseite durch die Anbringung eines Links (Verweis im Internet) die Inhalte der gelinkten Seite ggf. mit zu verantworten hat. Dies kann - so das Landgericht Hamburg - nur dadurch verhindert werden, dass der Betreiber sich ausdrücklich von diesen Inhalten distanziert. In diesem Buch sind Verweise zu Seiten im Internet gelegt. Für alle diese Verweise gilt, dass die Verfasser hiermit ausdrücklich erklären, dass sie keinerlei Einfluss auf die Gestaltung und die Inhal- te der gelinkten Seiten haben und sich deshalb von allen Inhalten der gelinkten Seiten distanzieren, sofern diese gegen Menschenrechte, Menschenwürde, gute Sitten oder geltende Gesetze verstoßen. Diese Erklärung gilt für alle in diesem Buch angezeigten Verweise und für alle Inhalte der Seiten, zu denen verlinkt worden ist. Titelbild: Blick aus dem Dienstzimmer des Verfassers am 15.07.2005 © Gerd Tamke Inhaltsverzeichnis Zur Titelseite Göttinger Straßennamen Vorwort - Dr. Dagmar Schlapeit-Beck, Dezernentin für Kultur und Soziales - Zum Gebrauch von Straßennamen Hartmut Kompart, Leiter Fachdienst Bodenordnung, Vermessung und Geoinformation Entstehungsgeschichte des Buches und Danksagung Gerd Tamke Einführung Entwicklung der Straßenbenennung und der Hausnummerierung in Göttingen Das Stadtgebiet bis 1864 Das Stadtgebiet von 1864 bis 1964 In den Jahren 1964 und 1965 eingemeindete Ortsteile Zu den durch Gebietsreform 1973 eingemeindeten Orten Daten auswertungen Statistik der Benennungen Vorbemerkung Namensgruppen bei Göttinger Straßennamen Straßennamen mit Bezug zu Belegenheiten Straßennamen nach Bergen und Höhenzügen Straßennamen aus Flora und Fauna Straßennamen nach Gewässern Straßennamen mit historischem Bezug Straßenbenennungen nach Personen Benennungen nach Städten Andere Benennungen Tabellarische Übersicht der Gruppen Lokale Gruppenbildungen bei Straßennamen Personennamen in der Straßenbenennung Statistische Auswertung Straßenumbenennungen Die politische Straßenbenennung Die Benennungspraxis der Nationalsozialisten Entnazifizierung – Entmilitarisierung Die Bundesrepublik Sonstige Umbenennungen Umbenennungen bei Eingemeindungen Umbenennungen auf Antrag der Bürger Umbenennungen durch Formveränderungen: Zusammenlegungen oder Trennung Umbenennungen zu Ehren von Personen Benennungen zu Lebzeiten Zeitraum 1864 bis 1932 Zeitraum 1933 bis 1945 Erläuterungen zu den Straßennamen Hinweise zur Zwangsarbeit während des Dritten Reiches Erläuterung zu den heutigen Straßennamen Erläuterung zu den untergegangenen Straßennamen Göttinger Straßennamen tabellarisch mit Beschlussdaten und Ortsteilzugehörigkeit Literaturhinweise Die Verfasser Zurück zum Inhaltsverzeichnis Hinweis: Über die Suchfunktion (STRG+F) kann das Dokument auch nach individuellen Stichwor- ten durchsucht werden. Zurück zum Inhaltsverzeichnis Vorwort Straßennamen, d. h. die Benennung von Straßen, Plätzen und Wegen, gibt es wahrscheinlich schon so lange, wie es menschliche Siedlungen gibt. Historisch greifbar werden solche Namen wohl erstmals für die Städte der griechisch-römischen Antike, wobei sich die damaligen Bezeichnungen auf die religiöse, politische, wirtschaftliche und militärische Funktion oder auf die topografischen Besonderheiten der Straßen bezogen. Daran änderte sich auch im europäischen Mittelalter wenig. Die Straßen des mittelalterlichen Göttingens sind dafür ein gutes Beispiel. Da gibt es den Markt und die Jüdenstraße, die Burgstraße und die Barfüßerstraße, die Weender und die Lange Geismarstraße. Die Beispiele Karspüle und Masch verweisen auf die Nähe der Straßenbezeichnungen zu den Flurnamen. Wer sich im übrigen spätestens jetzt verwundert fragt, was diese Namen denn bedeuten mögen, dem geben „Die Göttinger Straßennamen“ erschöpfende Auskunft. Zwar haben einzelne Straßen im Laufe der Zeit ihre Bezeichnung gewechselt, vereinzelt kamen auch neue Straßen oder Plätze mit jeweils eigenen Namen hinzu. Eine grundlegende Veränderung setzte jedoch erst im Zuge der Industrialisierung seit der 2. Hälfte des 19. Jahrhunderts ein. Wie die meisten Städte in Deutschland sprengte jetzt auch Göttingen seine durch den Wall markierte mittelalterliche Grenze und breitete sich rasch in das Umland aus. Neue Stadtviertel wurden angelegt, neue Straßen vermessen und gebaut. Erstmals in der Geschichte ergab sich jetzt die Notwendigkeit, innerhalb kurzer Zeit viele Straßen und Plätze neu zu benennen. Die Entscheidungshoheit darüber fiel wie selbstverständlich der Stadtobrigkeit zu. Als Fundus, aus dem diese die Namen schöpfte, setzten sich schnell die Flurbezeichnungen und die Namen bedeutender oder prominenter Persönlichkeiten durch. Vor allem durch die Benennung nach Personen luden die Straßennamen sich nun plötzlich mit einer ganz neuen kulturellen und im engeren Sinne politischen Bedeutung auf. Zwei der frühesten Benennungen dieser Art können als Beispiel dienen: die Bürgerstraße, benannt 1864 nach dem Dichter Gottfried August Bürger, und die Bertheaustraße, benannt 1883 nach Ernst Bertheau, Theologieprofessor und enger Vertrauter von Oberbürgermeister Georg Merkel. Die Benennung von Straßen und Plätzen bot jetzt die Möglichkeit, ein kulturelles oder politisches Zeichen zu setzen. Vor dem Hintergrund der tiefgreifenden politischen und kulturellen Umbrüche im 20. Jahrhundert verwundert es nicht, dass sich nun ein weiteres neues Phänomen beobachten lässt: die Umbenennung von Straßen. Besonders radikal bedienten sich die Nationalsozialisten dieses Instruments: Unter ihrer Herrschaft wurde aus dem Theaterplatz der Adolf-Hitler-Platz und aus der Weender Straße die Straße der SA. Nach 1945 wurden diese Umbenennungen wieder rückgängig gemacht. Die Benennung von Straßen nach Persönlichkeiten steht jedoch auch für eine Bewertung aus Sicht der jeweiligen Zeit, die im Nachhinein zuweilen Zweifel aufwirft. Auch mit diesem Thema setzt sich der vorliegende Band aktiv auseinander und leistet einen qualifizierten Diskussionsbeitrag. Auch heute noch sind Straßennamen ein wichtiges Mittel, gesellschaftlich anerkannte Personen zu ehren und so zugleich das Gesicht einer Stadt zu prägen. In der Benennung von Straßen findet das Selbstverständnis einer Bürgerschaft seinen Ausdruck. Umso größer ist der Dank, den wir Herrn Gerd Tamke und Herrn Rainer Driever schulden, die die vorliegende Publikation „Die Göttinger Straßennamen“ erarbeitet haben. Sie haben damit nicht nur ein unverzichtbares Nachschlagewerk für jeden an der Göttinger Geschichte Interessierten geschaffen. Die „Göttinger Straßennamen“ eröffnen darüber hinaus faszinierende Einblicke in kulturelle Prozesse und politische Umbrüche seit dem ausgehenden 19.Jahrundert. Dr. Dagmar Schlapeit-Beck Dezernentin für Kultur und Soziales zurück zum Inhaltsverzeichnis Zum Gebrauch von Straßennamen Straßennamen dienen auch heute noch in erster Linie als Adressenbestandteil der Navigation. Eine neue Straße erhält einen Namen und wird damit zu einem auffindbaren geografischen Objekt. Dort, wo die Grundrisse der Ortschaften neu geplant wurden, wie in den heutigen Großstädten der USA, begnügte man sich oftmals mit einer einfachen Straßennummerierung. Doch auch hier entstand eine Individualisierung, wie die namhafte „5th Avenue“ in New York zeigt. So bildet sich überall schnell aus einem Straßennamen eine „gute Adresse“, eine eigene Identität. Vielfach lässt sich jedoch nur noch erahnen, woher so mancher Straßenname stammt. Fehldeutun- gen sind sehr häufig und oft auch durch die Veränderungen der Sprache entstanden. Anfragen nach dem Ursprung von Straßennamen gehören daher für die städtische Vermessungsbehörde, als Ver- walter der Straßendatenbank, zum Alltag. Ich danke daher Herrn Gerd Tamke, dass er seine während seiner dreißigjährigen Dienstzeit bei der Stadt Göttingen erworbenen Kenntnisse genutzt hat, zusammen mit Herrn Dr. Rainer Driever, einen umfassenden Gesamtkatalog über die Göttinger Straßennamen und ihre Geschichte aufzustellen und diesen für eine zukünftige Weiterführung dem Fachdienst Bodenordnung, Vermessung und Geoin- formation zur Verfügung stellt. Von unschätzbarem Wert sind dabei jedoch auch die zahlreichen Querverweise und Bezüge zu Umbenennungen, da sie die Rückverfolgung alter Adressbestände dauerhaft erleichtern werden. Hartmut Kompart Leiter Fachdienst Bodenordnung, Vermessung und Geoinformation zurück zum Inhaltsverzeichnis Entstehungsgeschichte des Buches und Danksagung zurück zum Inhaltsverzeichnis Vor über dreißig Jahren kam mir der Gedanke, über alle Straßennamen Göttingens ein Buch zu schreiben, um den Auskunftswünschen der Göttinger Bürger nach zu kommen, welche mich als da- mals zuständigen Amtsleiter bei der Stadt Göttingen anriefen und nach den Gründen der jeweiligen Straßenbenennung fragten. Dieses Bedürfnis war verständlich, zu mal die Literatur über Straßenbe- nennungen sich im bereits 1953 erschienenen Buch Das Tausendjährige Göttingen von Jäger, Dep- pe und Troe erschöpfte, welches überdies vergriffen war und auch nicht mehr aufgelegt worden ist. Zudem waren die in den Jahren um 1960 in der Presse erschienenen Artikel meines Vorvorgängers im Amt, Horst Michling, in der Regel auch nicht mehr bekannt. In der Zwischenzeit
Recommended publications
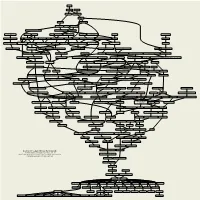
  • Academic Genealogy of George Em Karniadakis

    Academic Genealogy of George Em Karniadakis

    Nilos Kabasilas Demetrios Kydones Elissaeus Judaeus Manuel Chrysoloras Georgios Plethon Gemistos 1380, 1393 Basilios Bessarion 1436 Mystras Guarino da Verona Johannes Argyropoulos 1408 1444 Università di Padova Vittorino da Feltre Cristoforo Landino Marsilio Ficino 1416 Università di Padova 1462 Università di Firenze Ognibene (Omnibonus Leonicenus) Bonisoli da Lonigo Theodoros Gazes Angelo Poliziano Università di Mantova 1433 Constantinople / Università di Mantova 1477 Università di Firenze Leo Outers Alessandro Sermoneta Gaetano da Thiene Moses Perez Scipione Fortiguerra Demetrios Chalcocondyles Jacob ben Jehiel Loans Rudolf Agricola Thomas à Kempis Heinrich von Langenstein 1485 Université Catholique de Louvain 1493 Università di Firenze 1452 Mystras / Accademia Romana 1478 Università degli Studi di Ferrara 1363, 1375 Université de Paris Maarten (Martinus Dorpius) van Dorp Pelope Pietro Roccabonella Nicoletto Vernia François Dubois Jean Tagault Girolamo (Hieronymus Aleander) Aleandro Janus Lascaris Matthaeus Adrianus Johann (Johannes Kapnion) Reuchlin Jan Standonck Alexander Hegius Johannes von Gmunden 1504, 1515 Université Catholique de Louvain Università di Padova Università di Padova 1516 Université de Paris 1499, 1508 Università di Padova 1472 Università di Padova 1477, 1481 Universität Basel / Université de Poitiers 1474, 1490 Collège Sainte-Barbe / Collège de Montaigu 1474 1406 Universität Wien Niccolò Leoniceno Jacobus (Jacques Masson) Latomus Desiderius Erasmus Petrus (Pieter de Corte) Curtius Pietro Pomponazzi Jacobus (Jacques
  • Classics in Mathematics Richard Courant· Fritz John Introduction To

    Classics in Mathematics Richard Courant· Fritz John Introduction To

    Classics in Mathematics Richard Courant· Fritz John Introduction to Calculus and Analysis Volume I Springer-V erlag Berlin Heidelberg GmbH Richard Courant • Fritz John Introd uction to Calculus and Analysis Volume I Reprint of the 1989 Edition Springer Originally published in 1965 by Interscience Publishers, a division of John Wiley and Sons, Inc. Reprinted in 1989 by Springer-Verlag New York, Inc. Mathematics Subject Classification (1991): 26-XX, 26-01 Cataloging in Publication Data applied for Die Deutsche Bibliothek - CIP-Einheitsaufnahme Courant, Richard: Introduction to calcu1us and analysis / Richard Courant; Fritz John.- Reprint of the 1989 ed.- Berlin; Heidelberg; New York; Barcelona; Hong Kong; London; Milan; Paris; Singapore; Tokyo: Springer (Classics in mathematics) VoL 1 (1999) ISBN 978-3-540-65058-4 ISBN 978-3-642-58604-0 (eBook) DOI 10.1007/978-3-642-58604-0 Photograph of Richard Courant from: C. Reid, Courant in Gottingen and New York. The Story of an Improbable Mathematician, Springer New York, 1976 Photograph of Fritz John by kind permission of The Courant Institute of Mathematical Sciences, New York ISSN 1431-0821 This work is subject to copyright. All rights are reserved. whether the whole or part of the material is concemed. specifically the rights of trans1ation. reprinting. reuse of illustrations. recitation. broadcasting. reproduction on microfilm or in any other way. and storage in data banks. Duplication of this publication or parts thereof is permitted onlyunder the provisions of the German Copyright Law of September 9.1965. in its current version. and permission for use must always be obtained from Springer-Verlag. Violations are Iiable for prosecution under the German Copyright Law.
  • Kunstinstitutionen Zur Entstehung Und Etablierung Des Modernen Kunstbetriebs

    Kunstinstitutionen Zur Entstehung Und Etablierung Des Modernen Kunstbetriebs

    BIRGIT JOOSS KUNSTINSTITUTIONEN ZUR ENTSTEHUNG UND ETABLIERUNG DES MODERNEN KUNSTBETRIEBS Allgemein gilt das 19. Jh. als das Jahrhundert der Institu­ aufstellten und einen enormen Zulauf erfuhren. Sie alle tionalisierung von Kunst: Zum einen erlangten Akademien trugen zur Expansion einer medialen und zunehmend und Kunstschulen eine Vorrangstellung in der Ausbildung kommerzialisierten Kunstwelt bei.l und Produktion von Kunst, zum anderen sorgten Museen Allgemein betrachtet dient eine Institution der Fest­ und Ausstellungshäuser für ihre Publizität und Vermark­ schreibung von Handlungs- und Beziehungsmustern, der tung. Auch die sich formierenden Universitätsinstitute, an Aufstellung und Kontrolle von Regeln sowie der Qualitäts• denen sich das Fach Kunstgeschichte allmählich als wissen­ sicherung. Da sie gemeinhin die Lebensspanne ihrer Mit­ schaftliche Disziplin etablierte, sowie die Instanzen Kunst­ glieder übertrifft, steht sie - positiv formuliert - für die kritik und Kunstmarkt bestimmten zunehmend den Kreis­ generationsübergreifende Dauerhaftigkeit und Verlässlich• lauf des Kunstbetriebs und damit auch die Ausbildung eines keit ihrer Regeln, im negativen Sinne dagegen für Starrheit gültigen Kanons der Kunst. Die Institutionen setzten die und Reformresistenz. Bestimmend sind stets Individuen Unterschiede zwischen Kunst und Nicht-Kunst, zwischen und Institutionen gleichermaßen, die in enger Beziehung Professionalität und Dilettantismus. zueinander stehen und im Idealfall die fachliche Kompe­ Hatte am Ende des 18. Jhs. die Französische
  • Wie Die Kunstlerkolonie Worpswede Entstand

    Wie Die Kunstlerkolonie Worpswede Entstand

    !"#$!%#$!&'()*+$,-.+.(#$!".,/)0$%$ $(*)*1(%! ! !! !"#$%&#'%()*+$ ,-.)/%0#/#%1)$&#%2345%6'%78$*9:;.<#$'%=#"+$#'>%?$%6/*%@$>%A96->%)'&%1.$%.-/% B)'/*96/*+$6C#$%8"#$%D./*%&$#6%E.9$F#9'*#%.G%H#$G.'6/I9#'%J.*6+'.-G)/#)G%6'%J8$'"#$=% *K*6=> ,-.)/%0#/#%6/*%()*+$%F.9-$#6I9#$%0)"-6C.*6+'#'%F)$%&#)*/I9#'%B)'/*L%)'&%B)-*)$=#/I96I9*#% G6*%&#'%MI91#$A)'C*#'%E)=#'&/*6-%)'&%B8'/*-#$C+-+'6#'>% Wie die Künstlerkolonie Worpswede entstand von Claus Pese Die Literatur über die Künstlerkolonie Worpswede ist Legion. Dieser Artikel widmet sich der Frühzeit ihrer Entstehung. Er schließt mit einer Charakteristik der örtlichen Situation, wie sie sich heute darstellt. Einführung Bisher ist dieser Artikel nur in dem Katalog zur Ausstellung „Paula Modersohn-Becker och konstnärskolonin i Worpswede“ auf den Seiten 41 bis 62 in schwedischer Sprache erschienen. Die Ausstellung wurde vom 15. September 2018 bis zum 27. Januar 2019 in dem Stockholmer Kulturinstitut „Prins Eugens Waldemarsudde“ gezeigt. Künstlerkolonien – ein europäisches Phänomen Künstlerkolonien, im Wesentlichen während der 2. Hälfte des 19. Jahrhunderts entstanden, sind ein kunst- und kulturgeschichtliches Phänomen von gesamteuropäischer Dimension. Das Schaffen in Künstlerkolonien beschränkte sich keineswegs auf Malerei und Grafik, sondern konnte neben der bildenden Kunst gesellschaftspolitische Utopien, Literatur, Musik und darstellende Künste umfassen. Worpswede ist ein herausragendes Beispiel für eine Künstlerkolonie. In den Künstlerkolonien waren hauptsächlich akademisch ausgebildete Maler tätig, die sich vom Akademiebetrieb ebenso wie von der Zivilisation der technisierten Gesellschaft abgewandt hatten und den Großstädten den Rücken kehrten. In ihrem Glauben an die ewigen Gesetze der Natur gingen diese Künstler auf das Land, um sich dort dem Studium der Natur sowie der unverfälschten Sitten und Gebräuche der Bevölkerung zu widmen und dem Leben eine neue Natürlichkeit zu geben.
  • Mathematisches Forschungsinstitut Oberwolfach Emigration Of

    Mathematisches Forschungsinstitut Oberwolfach Emigration Of

    Mathematisches Forschungsinstitut Oberwolfach Report No. 51/2011 DOI: 10.4171/OWR/2011/51 Emigration of Mathematicians and Transmission of Mathematics: Historical Lessons and Consequences of the Third Reich Organised by June Barrow-Green, Milton-Keynes Della Fenster, Richmond Joachim Schwermer, Wien Reinhard Siegmund-Schultze, Kristiansand October 30th – November 5th, 2011 Abstract. This conference provided a focused venue to explore the intellec- tual migration of mathematicians and mathematics spurred by the Nazis and still influential today. The week of talks and discussions (both formal and informal) created a rich opportunity for the cross-fertilization of ideas among almost 50 mathematicians, historians of mathematics, general historians, and curators. Mathematics Subject Classification (2000): 01A60. Introduction by the Organisers The talks at this conference tended to fall into the two categories of lists of sources and historical arguments built from collections of sources. This combi- nation yielded an unexpected richness as new archival materials and new angles of investigation of those archival materials came together to forge a deeper un- derstanding of the migration of mathematicians and mathematics during the Nazi era. The idea of measurement, for example, emerged as a critical idea of the confer- ence. The conference called attention to and, in fact, relied on, the seemingly stan- dard approach to measuring emigration and immigration by counting emigrants and/or immigrants and their host or departing countries. Looking further than this numerical approach, however, the conference participants learned the value of measuring emigration/immigration via other less obvious forms of measurement. 2892 Oberwolfach Report 51/2011 Forms completed by individuals on religious beliefs and other personal attributes provided an interesting cartography of Italian society in the 1930s and early 1940s.
  • Implications for Understanding the Role of Affect in Mathematical Thinking

    Implications for Understanding the Role of Affect in Mathematical Thinking

    Mathematicians and music: Implications for understanding the role of affect in mathematical thinking Rena E. Gelb Submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy under the Executive Committee of the Graduate School of Arts and Sciences COLUMBIA UNIVERSITY 2021 © 2021 Rena E. Gelb All Rights Reserved Abstract Mathematicians and music: Implications for understanding the role of affect in mathematical thinking Rena E. Gelb The study examines the role of music in the lives and work of 20th century mathematicians within the framework of understanding the contribution of affect to mathematical thinking. The current study focuses on understanding affect and mathematical identity in the contexts of the personal, familial, communal and artistic domains, with a particular focus on musical communities. The study draws on published and archival documents and uses a multiple case study approach in analyzing six mathematicians. The study applies the constant comparative method to identify common themes across cases. The study finds that the ways the subjects are involved in music is personal, familial, communal and social, connecting them to communities of other mathematicians. The results further show that the subjects connect their involvement in music with their mathematical practices through 1) characterizing the mathematician as an artist and mathematics as an art, in particular the art of music; 2) prioritizing aesthetic criteria in their practices of mathematics; and 3) comparing themselves and other mathematicians to musicians. The results show that there is a close connection between subjects’ mathematical and musical identities. I identify eight affective elements that mathematicians display in their work in mathematics, and propose an organization of these affective elements around a view of mathematics as an art, with a particular focus on the art of music.
  • Professor Richard Courant (1888 – 1972)

    Professor Richard Courant (1888 – 1972)

    Professor Richard Courant (1888 – 1972) From Wikipedia, the free encyclopedia, http://en.wikipedia.org/wiki/Richard_Courant Field: Mathematics Institutions: University of Göttingen University of Münster University of Cambridge New York University Alma mater: University of Göttingen Doctoral advisor: David Hilbert Doctoral students: William Feller Martin Kruskal Joseph Keller Kurt Friedrichs Hans Lewy Franz Rellich Known for: Courant number Courant minimax principle Courant–Friedrichs–Lewy condition Biography: Courant was born in Lublinitz in the German Empire's Prussian Province of Silesia. During his youth, his parents had to move quite often, to Glatz, Breslau, and in 1905 to Berlin. He stayed in Breslau and entered the university there. As he found the courses not demanding enough, he continued his studies in Zürich and Göttingen. Courant eventually became David Hilbert's assistant in Göttingen and obtained his doctorate there in 1910. He had to fight in World War I, but he was wounded and dismissed from the military service shortly after enlisting. After the war, in 1919, he married Nerina (Nina) Runge, a daughter of the Göttingen professor for Applied Mathematics, Carl Runge. Richard continued his research in Göttingen, with a two-year period as professor in Münster. There he founded the Mathematical Institute, which he headed as director from 1928 until 1933. Courant left Germany in 1933, earlier than many of his colleagues. While he was classified as a Jew by the Nazis, his having served as a front-line soldier exempted him from losing his position for this particular reason at the time; however, his public membership in the social-democratic left was a reason for dismissal to which no such exemption applied.[1] After one year in Cambridge, Courant went to New York City where he became a professor at New York University in 1936.
  • Chronological List of Correspondence, 1895–1920

    Chronological List of Correspondence, 1895–1920

    CHRONOLOGICAL LIST OF CORRESPONDENCE, 1895–1920 In this chronological list of correspondence, the volume and document numbers follow each name. Documents abstracted in the calendars are listed in the Alphabetical List of Texts in this volume. 1895 13 or 20 Mar To Mileva Maric;;, 1, 45 29 Apr To Rosa Winteler, 1, 46 Summer To Caesar Koch, 1, 6 18 May To Rosa Winteler, 1, 47 28 Jul To Julia Niggli, 1, 48 Aug To Rosa Winteler, 5: Vol. 1, 48a 1896 early Aug To Mileva Maric;;, 1, 50 6? Aug To Julia Niggli, 1, 51 21 Apr To Marie Winteler, with a 10? Aug To Mileva Maric;;, 1, 52 postscript by Pauline Einstein, after 10 Aug–before 10 Sep 1,18 From Mileva Maric;;, 1, 53 7 Sep To the Department of Education, 10 Sep To Mileva Maric;;, 1, 54 Canton of Aargau, 1, 20 11 Sep To Julia Niggli, 1, 55 4–25 Nov From Marie Winteler, 1, 29 11 Sep To Pauline Winteler, 1, 56 30 Nov From Marie Winteler, 1, 30 28? Sep To Mileva Maric;;, 1, 57 10 Oct To Mileva Maric;;, 1, 58 1897 19 Oct To the Swiss Federal Council, 1, 60 May? To Pauline Winteler, 1, 34 1900 21 May To Pauline Winteler, 5: Vol. 1, 34a 7 Jun To Pauline Winteler, 1, 35 ? From Mileva Maric;;, 1, 61 after 20 Oct From Mileva Maric;;, 1, 36 28 Feb To the Swiss Department of Foreign Affairs, 1, 62 1898 26 Jun To the Zurich City Council, 1, 65 29? Jul To Mileva Maric;;, 1, 68 ? To Maja Einstein, 1, 38 1 Aug To Mileva Maric;;, 1, 69 2 Jan To Mileva Maric;; [envelope only], 1 6 Aug To Mileva Maric;;, 1, 70 13 Jan To Maja Einstein, 8: Vol.
  • De Analysi Per Aequationes Numero Terminorum Infinitas 1669 (Published 1711) After 1696, Master of the Mint

    De Analysi Per Aequationes Numero Terminorum Infinitas 1669 (Published 1711) After 1696, Master of the Mint

    Nick Trefethen Oxford Computing Lab Who invented the great numerical algorithms? Slides available at my web site: www.comlab.ox.ac.uk/nick.trefethen A discussion over coffee. Ivory tower or coal face? SOME MAJOR DEVELOPMENTS IN SCIENTIFIC COMPUTING (29 of them) Before 1940 Newton's method least-squares fitting orthogonal linear algebra Gaussian elimination QR algorithm Gauss quadrature Fast Fourier Transform Adams formulae quasi-Newton iterations Runge-Kutta formulae finite differences 1970-2000 preconditioning 1940-1970 spectral methods floating-point arithmetic MATLAB splines multigrid methods Monte Carlo methods IEEE arithmetic simplex algorithm nonsymmetric Krylov iterations conjugate gradients & Lanczos interior point methods Fortran fast multipole methods stiff ODE solvers wavelets finite elements automatic differentiation Before 1940 Newton’s Method for nonlinear eqs. Heron, al-Tusi 12c, Al Kashi 15c, Viète 1600, Briggs 1633… Isaac Newton 1642-1727 Mathematician and physicist Trinity College, Cambridge, 1661-1696 (BA 1665, Fellow 1667, Lucasian Professor of Mathematics 1669) De analysi per aequationes numero terminorum infinitas 1669 (published 1711) After 1696, Master of the Mint Joseph Raphson 1648-1715 Mathematician at Jesus College, Cambridge Analysis Aequationum universalis 1690 Raphson’s formulation was better than Newton’s (“plus simple” - Lagrange 1798) FRS 1691, M.A. 1692 Supporter of Newton in the calculus wars—History of Fluxions, 1715 Thomas Simpson 1710-1761 1740: Essays on Several Curious and Useful Subjects… 1743-1761:
  • Catalogue Number [Of the Bulletin]

    Catalogue Number [Of the Bulletin]

    BULLETIN OF WELLESLEY COLLEGE CATALOGUE NUMBER 1962-1963 WELLESLEY • MASSACHUSETTS CATALOGUE NUMBER BULLETIN OF WELLESLEY COLLEGE OCTOBER 30, 1962 Bulletins published six times a year by Wellesley College, Wellesley, Massachusetts. January, one; April, one; October, two; November, two. Second-Class postage paid at Boston, Massachusetts and at additional mailing offices. Volume 52 Number 2 . TABLE OF CONTENTS Visitors; Correspondence 5 Calendar 6 Board of Trustees 7 Faculty and Administration 8 The College 20 The Curriculum 24 Requirements for the BA. Degree 24 Research or Independent Study 28 Honors and Academic Awards 28 General Information 29 Course Examinations, Special Examinations, Advanced Place- ment, Use of the Summer Vacation, Summer Internship in Government, Junior Year Abroad Preparation for Graduate Study 31 College Teaching and Research, Other Professions, Teaching in Schools, Medical School, Hospital and Public Health Work, Civil Service Graduate Fellowships 32 Requirements for the MA. Degree 33 Courses of Instruction 34 Art 34 Interdepartmental Courses . 77 Astronomy 38 Italian 78 Biblical History 40 Latin 79 Botany and Bacteriology . 43 Mathematics 82 Chemistry 45 Music 84 Classical Archeology 48 Philosophy 87 Economics 49 Physical Education 89 Education 52 Physics 91 English 54 Political Science 92 French 60 Psychology 96 Geography 64 Russian 99 Geology 65 Sociology and Anthropology 100 German 67 Spanish 102 Greek 70 Speech 105 History 71 Zoology and Physiology 107 4 Contents Admission HI Of Freshmen HI Of Transfer Students
  • Einsteins Kolleginnen – Physikerinnen Gestern & Heute

    Einsteins Kolleginnen – Physikerinnen Gestern & Heute

    Einsteins Kolleginnen – Physikerinnen gestern & heute Prof. Dr. Cornelia Denz • Dr. Annette Vogt GEFÖRDERT VOM Impressum Herausgeber Kompetenzzentrum Technik – Diversity – Chancengleichheit e.V. Wilhelm-Bertelsmann-Str. 10 33602 Bielefeld www.kompetenzz.de © 2005 | Kompetenzzentrum Technik – Diversity – Chancengleichheit e.V. Gefördert durch das Bundesministerium für Familie, Senioren, Frauen und Jugend Konzeption Prof. Dr. Cornelia Denz Dr. Annette Vogt Barbara Schwarze Autorinnen Prof. Dr. Cornelia Denz Dr. Annette Vogt Koordinierung und Redaktion Dörte Jödicke Redaktionelle Mitarbeit Christina Mersch Textbearbeitung Inga Zeisberg Bildrecherche Anna Hájková Gestaltung und Produktion DesignWerkstatt 12: Katrin Berkenkamp ISBN: 3-933476-08-9 Vorwort Gender im Einsteinjahr – Physikerinnen gestern & heute Seit dem Jahr 2000 engagieren sich tausende Mitarbeiterinnen und Mitarbeiter von Forschungseinrich- tungen und Institutionen im Rahmen der »Wissenschaftsjahre« in Deutschland, um durch fantasievolle und kreative Veranstaltungen und Angebote das Interesse an Forschung und Technologie zu wecken. Ziel ist es, direkte Kontakte zu Wissenschaftlerinnen und Wissenschaftlern herzustellen und so die Bevölkerung Natur- wissenschaft und Technik konkreter erleben zu lassen. Laut »Eurobarometer« sind 37% der Bevölkerung in Deutschland an neuen Erfindungen und Technologien sehr interessiert. Die Wissenschaftsjahre richten sich auch gezielt an die jüngste Generation, den wissenschaftlichen Nach- wuchs: Es soll Lust gemacht werden auf eine Zukunft als Forscherin oder Forscher. Dabei ist die Rolle von Vorbildern besonders wichtig. Junge Leute, speziell junge Frauen, haben wenig Chancen, Physikerinnen im Beruf zu erleben, weil aktuell an deutschen Hochschulen weniger als 4% Professorinnen in der Physik lehren; dies sind nur 50 Professorinnen gegenüber 1.750 Professoren. Im »Einsteinjahr 2005« steht zum ersten Mal nicht ein Wissenschaftsgebiet, sondern eine berühmte Forscher- persönlichkeit im Mittelpunkt eines Wissenschaftsjahres.
  • Introduction Women Researchers in Industrial Laboratories: Trends And

    Introduction Women Researchers in Industrial Laboratories: Trends And

    INTRODUCTION WOMEN RESEARCHERS IN INDUSTRIAL LABORATORIES: TRENDS AND PERSPECTIVES Renate Tobies and Annette B. Vogt Our primary aim in this introduction is to formulate a number of theses regarding the factors and parameters that determined the careers of women in industrial laboratories during the first decades of the twentieth century. These theses derive from our own long-standing investigations about female scientists and female re- searchers and their career paths,1 on the chapters written by our colleagues in this book, and on the many discussions that this collaboration incited. Here we would like to describe the trends of this relatively new research field, to analyze its de- velopment, and to enumerate some of the overarching issues that have informed this book and that will prove relevant to further studies. The following theses can be thought of as a summary of Women in Industrial Research, and we hope that they might also serve to instigate discussions in the future. Thesis 1 Approximately from the year 1900 onwards, equal access to education at all school and university levels and access to academic careers were preconditions that enabled women to join industrial research laboratories. In countries where access to educational institutions, especially to universities, was less dependent on state regulations, some female scientists were able to ob- tain positions in engineering and industrial research laboratories. Based on in- ternational comparisons, Ilse Costas developed an explanatory model for women’s access to academic careers.2 For careers in industrial laboratories, our investiga- tions have confirmed that the preconditions in these fields were similar.