DOCSLIB.ORG

Summary of Useful Formulae

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Summary of Useful Formulae ME 24-221 Thermodynamics I Some Useful Formulae 1 Control Mass Continuity Equation m constant First Law £ 2 ¡ 2 £ ¢ ¢ m V V ¤ 2 1 ¡ ¡ U ¡ U mg Z Z Q W 2 1 2 2 1 ¤ 1 2 1 2 Compression-expansion work 2 ¦¥ 1W2 PdV 1 For polytropic procees, PV n c , P V ¡ P V 2 2 1 1 W n § 1 1 2 1 ¡ n V 2 P1V1ln n 1 V1 Second Law 2 δ Q ¢ ¨¥ S2 ¡ S1 1 S2 gen 1 T For isothermal process 2 δQ Q ¥ 1 2 1 T T For reversible process 1S2 gen 0 For adiabatic process 1Q2 0 Therefore, for a reversible adiabatic process S2 ¡ S1 0 ¡ s2 s1 0 Therefore, a reversible adiabatic process is an isentropic process. 1 2 Control Volume 2.1 Steady State Steady Flow (SSSF) Continuity ∑m˙ i ¡ ∑m˙ e 0 i e First Law 2 2 ¢ ¢ ¢ ¢ ¢ V V ¡ ∑m˙ h i gZ ∑m˙ h e gZ Q˙ ¡ W˙ 0 © i © i i e e e cv cv i 2 e 2 Second Law Q˙ ¢ ¢ j ¡ ˙ ∑m˙ isi ∑m˙ ese ∑ Sgen 0 i e j Tj Reversible process S˙gen 0 Adiabatic process Q˙ 0 For one inlet-one outlet device, a reversible adiabatic process is therefore an isentropic process, with si se 2.2 Uniform State Uniform Flow (USUF) Continuity £ ¡ m ¡ m ∑m ∑m 2 1 ¤ i e i e First Law 2 2 2 2 ¢ ¢ ¢ ¢ ¢ ¢ ¢ ¢ ¢ V V V V ¡ ¡ m u 2 gZ ¡ m u 1 gZ ∑m h i gZ ∑m h e gZ Q W © © © 2 © 2 2 1 1 1 i i i e e e cv cv 2 2 i 2 e 2 Second Law t ˙ ¢ ¢ Q ¥ cv ¡ ¡ m2s2 m1s1 ∑misi ∑mese dt 1 S2 gen i e 0 T 3 Gibbs Equation ¢ T ds du Pdv dh ¡ vdP This equation holds true for all simple compressible substances. 2 4 Properties of Pure Substances 4.1 Vapor-Liquid Phase Equilibrium For a specific property φ (such as h,u,v,s etc) under the dome ¢ φ φ φ f x f g 4.2 Ideal Gas Ideal Gas Equations of State Pv RT du CvdT 2 ¥ u2 ¡ u1 CvdT 1 £ C T ¡ T if C is constant v 2 1 ¤ v dh CpdT 2 ¥ ¡ h2 h1 CpdT 1 £ C T ¡ T if C is constant p 2 1 ¤ p Specific Heats and Ideal Gas Constants Cp ¡ Cv R R R M Cp k Cv Entropy Relationships dT dP ds C ¡ R p T P 2 dT P ¥ ¡ ¡ 2 s2 s1 Cp Rln 1 T P1 T P 2 ¡ 2 Cpln Rln if constant Cp T1 P1 P ¡ s0 ¡ s0 Rln 2 otherwise T2 T1 P1 dT ¢ dv ds C R v T v 2 dT ¢ v ¥ ¡ 2 s2 s1 Cv Rln 1 T v1 T ¢ v 2 2 Cvln Rln if constant Cv T1 v1 3 Isentropic Process for Ideal Gas For variable specific heats P P 1 r1 P2 Pr2 v v 1 r1 v2 vr2 For constant specific heats Pvk constant P v k 1 2 © P2 v1 k 1 T P k 2 2 © T1 P1 T v k 1 2 1 © T1 v2 The above four relationships also hold for a reversible polytropic process with the polytropic exponent n replacing k. 4.3 Incompressible Substance Equation of State du dh CdT 2 ¥ ¡ ¡ u2 u1 h2 h1 CdT 1 £ C T ¡ T if C is constant 2 1 ¤ Entropy Relationships du ds T 2 dT ¥ s2 ¡ s1 C 1 T T Cln 2 if C is constant T1 C=constant can usually be assumed for incompressible substances. 4 5 Heat Engines, Heat Pumps and Refrigerators Thermal efficiency of heat engine W η net th QH Q ¡ Q H L QH Coefficient of Performance (C.O.P) of Heat Pump Q β H Wnet Q H QH ¡ QL Coefficient of Performance (C.O.P) of Refrigerator Q β L Wnet Q L QH ¡ QL Carnot Cycle Q T H H QL TL T η ¡ L th 1 TH T β H TH ¡ TL T β L TH ¡ TL 6 Isentropic Efficiency of Engineering Devices w η turbine ws w η s compressor w 2 V 2 η e nozzle 2 Ves 2 5 7 Irreversibility and Availability Availability: ¡ ¡ Ψ ¡ h T s h T s 0 re f 0 re f Irreversibility: ˙ ˙ I T0Sgen ˙ ˙ Work in an SSSF process with heat gain QH from TH and heat loss Q0 to T0: T ¢ ¡ ¡ 0 ¡ W˙ Q˙ 1 m˙ Ψ Ψ I˙ net H © i e TH Second Law Efficiency (Effectiveness) Turbine: W˙ η net 2 Ψ ¡ Ψ m˙ i e Compressor: Ψ ¡ Ψ m˙ η i e 2 W˙ net 8 Power and Refrigeration Cycles 8.1 Ideal Rankine Cycle p=c p=c 3 T 2 1 4 s 1-2:Isentropic compression in pump 2-3: Constant pressure heat addition in boiler 3-4: Isentropic expansion in turbine 4-1: Constant pressure heat rejection in condenser Working fluid is usually water or other two-phase substance 6 Work and heat transfer formulae: ¡ wp h1 h2 £ v P ¡ P 1 1 2 ¤ ¡ qb h3 h2 ¡ wT h3 h4 ¡ qc h1 h4 Also s1 s2 s3 s4 8.2 Ideal Air Standard Brayton Cycle p=c 3 T 2 p=c 4 1 s 1-2:Isentropic compression in compressor 2-3: Constant pressure heat addition in heat exchanger 3-4: Isentropic expansion in turbine 4-1: Constant pressure heat rejection in heat exchanger Working fluid idealized to be air Work and heat transfer formulae: ¡ wC h1 h2 ¡ qh h3 h2 wT h3 ¡ h4 ¡ qc h1 h4 Also s1 s2 s3 s4 7 For constant Cp £ w C T ¡ T C p 1 2 ¤ £ q C T ¡ T h p 3 2 ¤ £ w C T ¡ T T p 3 4 ¤ £ q C T ¡ T c p 1 4 ¤ Also k 1 T P k 2 2 © T1 P1 k 1 T P k 4 4 © T3 P3 For variable Cp P P r2 2 Pr1 P1 P P r4 4 Pr3 P3 Thermal efficiency of Brayton cycle (For constant Cp) T η ¡ 1 th 1 T2 k 1 P k 1 ¡ 1 © P2 8.3 Ideal Air Standard Otto Cycle v =c 3 T 2 v = c 4 1 s Otto cycle is a piston-cylinder cycle (control mass) Models spark ignition (SI) engines 1-2:Isentropic compression 8 2-3: Constant volume heat addition 3-4: Isentropic expansion 4-1: Constant volume heat rejection Working fluid idealized to be air Process 1-2: s1 s2 k 1 T P k 2 2 i f C constant © p T1 P1 T V k 1 2 1 i f C constant © p T1 V2 ¡ ¡ u2 u1 1w2 £ C T ¡ T i f C constant v 2 1 ¤ p Process 2-3: ¡ u3 u2 2q3 £ C T ¡ T i f C constant v 3 2 ¤ p Process 3-4: s3 s4 k 1 T P k 4 4 i f C constant © p T3 P3 T V k 1 4 3 i f C constant © p T3 V4 ¡ ¡ u4 u3 3w4 £ C T ¡ T i f C constant v 4 3 ¤ p Process 4-1: ¡ u1 u4 1q4 £ C T ¡ T i f C constant v 1 4 ¤ p Thermal efficiency of Otto cycle (For constant Cp) T η ¡ 1 th 1 T2 V 1 k 1 ¡ 1 © V2 1 k ¡ 1 rv where rv is the compression ratio. Mean Effective Pressure: w mep net ¡ v1 v2 9 8.4 Ideal Air Standard Diesel Cycle 3 p=c 2 T v = c 4 1 s Diesel cycle is a piston-cylinder cycle (control mass) Models compression ignition (CI) engines 1-2:Isentropic compression 2-3: Constant pressure heat addition 3-4: Isentropic expansion 4-1: Constant volume heat rejection Working fluid idealized to be air Process 1-2: s1 s2 k 1 T P k 2 2 i f C constant © p T1 P1 T V k 1 2 1 i f C constant © p T1 V2 ¡ u2 ¡ u1 1w2 £ C T ¡ T i f C constant v 2 1 ¤ p Process 2-3: h3 ¡ h2 2q3 £ C T ¡ T p 3 2 ¤ Process 3-4: s3 s4 k 1 T P k 4 4 i f C constant © p T3 P3 T V k 1 4 3 i f C constant © p T3 V4 ¡ ¡ u4 u3 3w4 £ C T ¡ T i f C constant v 4 3 ¤ p 10 Process 4-1: u1 ¡ u4 1q4 £ C T ¡ T i f C constant v 1 4 ¤ p Thermal efficiency of Otto cycle (For constant Cp) £ C T ¡ T v ¤ ¡ 4 1 η 1 £ th C T ¡ T p 3 2 ¤ 8.5 Ideal Vapor Refrigeration Cycle p=c p=c 2 T 3 1 4 s Simply Rankine cycle run backwards Note how points 1,2,3,4 have been shifted 1-2:Isentropic compression in compressor 2-3: Constant pressure heat loss at high-temperature source 3-4: Isentropic expansion in expansion valve 4-1: Constant pressure heat gain in evaporator Working fluid is usually refrigerant or other two-phase substance 11.
Load more

Recommended publications
  • Polytropic Processes
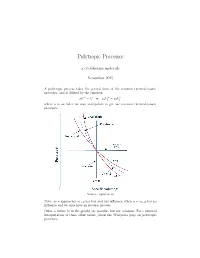
    Polytropic Processes a.cyclohexane.molecule November 2015 A polytropic process takes the general form of the common thermodynamic processes, and is defined by the equation n n n pV = C or p1V1 = p2V2 where n is an index we may manipulate to get our common thermodynamic processes. Source: nptel.ac.in Note: as n approaches 1, p has less and less influence; when n = 1, p has no influence and we thus have an isobaric process. Other n values (x in the graph) are possible, but not common. For a physical interpretation of these other values, check the Wikipedia page on polytropic processes. Because polytropic processes are general representations of thermodynamic pro- cesses, any quantities we calculate for a polytropic process will be a general equation for that quantity in all other thermodynamic processes. We proceed to find the work and heat associated with a polytropic process. We start with the definition of work: Z V2 w = − p dV V1 The polytropic equation pV n = C allows us to manipulate our formula for work in the following manner, as long as n 6= 1 V V Z 2 C Z 2 C V C V w = − dV = −C V −n dV = − V 1−n 2 = V 1−n 2 n V1 V1 V1 V V1 1 − n n − 1 Evaluating this expression, C CV 1−n − CV 1−n w = V 1−n − V 1−n = 2 1 n − 1 2 1 n − 1 n n We let the first C be p2V2 and the second C be p1V1 , such that the exponents cancel to obtain p V nV 1−n − p V nV 1−n p V − p V R(T − T ) w = 2 2 2 1 1 1 = 2 2 1 1 = 2 1 n − 1 n − 1 n − 1 where the last equality follows from the ideal gas law pV = RT and our deriva- tion for the work of a polytropic process is complete.
    [Show full text]
  • MECH 230 – Thermodynamics 1 Final Workbook Solutions
    MECH 230 – Thermodynamics 1 Final Workbook Solutions CREATED BY JUSTIN BONAL MECH 230 Final Exam Workbook Contents 1.0 General Knowledge ........................................................................................................................... 1 1.1 Unit Analysis .................................................................................................................................. 1 1.2 Pressure ......................................................................................................................................... 1 2.0 Energies ............................................................................................................................................ 2 2.1 Work .............................................................................................................................................. 2 2.2 Internal Energy .............................................................................................................................. 3 2.3 Heat ............................................................................................................................................... 3 2.4 First Law of Thermodynamics ....................................................................................................... 3 3.0 Ideal gas ............................................................................................................................................ 4 3.1 Universal Gas Constant .................................................................................................................
    [Show full text]
  • 3. Thermodynamics Thermodynamics
    Design for Manufacture 3. Thermodynamics Thermodynamics • Thermodynamics – study of heat related matter in motion. • Ma jor deve lopments d uri ng 1650 -1850 • Engineering thermodynamics mainly concerned with work produc ing or utili si ng machi nes such as - Engines, - TbiTurbines and - Compressors together w ith th e worki ng sub stances used i n th e machi nes. • Working substance – fluids: capable of deformation, energy transfer • Air an d s team are common wor king sub st ance Design and Manufacture Pressure F P = A Force per unit area. Unit: Pascal (Pa) N / m 2 1 Bar =105 Pa 1 standard atmosphere = 1.01325 Bar 1 Bar =14.504 Psi (pound force / square inch, 1N= 0.2248 pound force) 1 Psi= 6894.76 Pa Design and Manufacture Phase Nature of substance. Matter can exists in three phases: solid, liquid and gas Cycle If a substance undergoes a series of processes and return to its original state, then it is said to have been taken through a cycle. Design for Manufacture Process A substance is undergone a process if the state is changed by operation carried out on it Isothermal process - Constant temperature process Isobaric process - Constant pressure process Isometric process or isochoric process - Constant volume process Adiabatic Process No heat is transferred, if a process happens so quickly that there is no time to transfer heat, or the system is very well insulated from its surroundings. Polytropic process Occurs with an interchange of both heat and work between the system and its surroundings E.g. Nonadiabatic expansion or compression
    [Show full text]
  • Chapter 7 BOUNDARY WORK
    Chapter 7 BOUNDARY WORK Frank is struck - as if for the first time - by how much civilization depends on not seeing certain things and pretending others never occurred. − Francine Prose (Amateur Voodoo) In this chapter we will learn to evaluate Win, which is the work term in the first law of thermodynamics. Work can be of different types, such as boundary work, stirring work, electrical work, magnetic work, work of changing the surface area, and work to overcome friction. In this chapter, we will concentrate on the evaluation of boundary work. 110 Chapter 7 7.1 Boundary Work in Real Life Boundary work is done when the boundary of the system moves, causing either compression or expansion of the system. A real-life application of boundary work, for example, is found in the diesel engine which consists of pistons and cylinders as the prime component of the engine. In a diesel engine, air is fed to the cylinder and is compressed by the upward movement of the piston. The boundary work done by the piston in compressing the air is responsible for the increase in air temperature. Onto the hot air, diesel fuel is sprayed, which leads to spontaneous self ignition of the fuel-air mixture. The chemical energy released during this combustion process would heat up the gases produced during combustion. As the gases expand due to heating, they would push the piston downwards with great force. A major portion of the boundary work done by the gases on the piston gets converted into the energy required to rotate the shaft of the engine.
    [Show full text]
  • Heat Transfer During the Piston-Cylinder Expansion of a Gas
    AN ABSTRACT OF THE THESIS OF Matthew Jose Rodrigues for the degree of Master of Science in Mechanical Engineering presented on June 5, 2014. Title: Heat Transfer During the Piston-Cylinder Expansion of a Gas Abstract approved: ______________________________________________________ James A. Liburdy The expansion of a gas within a piston-cylinder arrangement is studied in order to obtain a better understanding of the heat transfer which occurs during this process. While the situation of heat transfer during the expansion of a gas has received considerable attention, the process is still not very well understood. In particular, the time dependence of heat transfer has not been well studied, with many researchers instead focused on average heat transfer rates. Additionally, many of the proposed models are not in agreement with each other and are usually dependent on experimentally determined coefficients which have been found to vary widely between test geometries and operating conditions. Therefore, the expansion process is analyzed in order to determine a model for the time dependence of heat transfer during the expansion. A model is developed for the transient heat transfer by assuming that the expansion behaves in a polytropic manner. This leads to a heat transfer model written in terms of an unknown polytropic exponent, n. By examining the physical significance of this parameter, it is proposed that the polytropic exponent can be related to a ratio of the time scales associated with the expansion process, such as a characteristic Peclet number. Experiments are conducted to test the proposed heat transfer model and to establish a relationship for the polytropic exponent.
    [Show full text]
  • Thermodynamic Analysis of an Irreversible Maisotsenko Reciprocating Brayton Cycle
    entropy Article Thermodynamic Analysis of an Irreversible Maisotsenko Reciprocating Brayton Cycle Fuli Zhu 1,2,3, Lingen Chen 1,2,3,* and Wenhua Wang 1,2,3 1 Institute of Thermal Science and Power Engineering, Naval University of Engineering, Wuhan 430033, China; [email protected] (F.Z.); [email protected] (W.W.) 2 Military Key Laboratory for Naval Ship Power Engineering, Naval University of Engineering, Wuhan 430033, China 3 College of Power Engineering, Naval University of Engineering, Wuhan 430033, China * Correspondence: [email protected] or [email protected]; Tel.: +86-27-8361-5046; Fax: +86-27-8363-8709 Received: 20 January 2018; Accepted: 2 March 2018; Published: 5 March 2018 Abstract: An irreversible Maisotsenko reciprocating Brayton cycle (MRBC) model is established using the finite time thermodynamic (FTT) theory and taking the heat transfer loss (HTL), piston friction loss (PFL), and internal irreversible losses (IILs) into consideration in this paper. A calculation flowchart of the power output (P) and efficiency (η) of the cycle is provided, and the effects of the mass flow rate (MFR) of the injection of water to the cycle and some other design parameters on the performance of cycle are analyzed by detailed numerical examples. Furthermore, the superiority of irreversible MRBC is verified as the cycle and is compared with the traditional irreversible reciprocating Brayton cycle (RBC). The results can provide certain theoretical guiding significance for the optimal design of practical Maisotsenko reciprocating gas turbine plants. Keywords: finite-time thermodynamics; irreversible Maisotsenko reciprocating Brayton cycle; power output; efficiency 1. Introduction The revolutionary Maisotsenko cycle (M-cycle), utilizing the psychrometric renewable energy from the latent heat of water evaporating, was firstly provided by Maisotsenko in 1976.
    [Show full text]
  • Quantum Mechanics Polytropic Process
    Quantum Mechanics_polytropic process A polytropic process is a thermodynamic process that obeys the relation: where p is the pressure, v is specific volume, n, the polytropic index, is any real number, andC is a constant. The polytropic process equation is particularly useful for characterizing expansion and compression processes which include heat transfer. This equation can accurately characterize a very wide range ofthermodynamic processes, that range from n<0 to n= which covers, n=0 (Isobaric), n=1 (Isothermal), n=γ (Isentropic), n= (Isochoric) processes and all values of n in between. Hence the equation is polytropic in the sense that it describes many lines or many processes. In addition to the behavior of gases, it can in some cases represent some liquids and solids. The one restriction is that the process should display an energy transfer ratio of K=δQ/δW=constant during that process. If it deviates from that restriction it suggests the exponent is not a constant. For a particular exponent, other points along the curve can be calculated: Derivation Polytropic processes behave differently with various polytropic indice. Polytropic process can generate other basic thermodynamic processes. The following derivation is taken from Christians.[1] Consider a gas in a closed system undergoing an internally reversible process with negligible changes in kinetic and potential energy. The First Law of Thermodynamics is Define the energy transfer ratio, . For an internally reversible process the only type of work interaction is moving boundary work, given by Pdv. Also assume the gas is calorically perfect (constant specific heat) so du = cvdT. The First Law can then be written (Eq.
    [Show full text]
  • Physico-Mathematical Model of a Hot Air Engine Using Heat from Low-Temperature Renewable Sources of Energy
    U.P.B. Sci. Bull., Series D, Vol. 78, Iss. D, 2016 ISSN 1223-7027 PHYSICO-MATHEMATICAL MODEL OF A HOT AIR ENGINE USING HEAT FROM LOW-TEMPERATURE RENEWABLE SOURCES OF ENERGY Vlad Mario HOMUTESCU1, Marius-Vasile ATANASIU2, Carmen-Ema PANAITE3, Dan-Teodor BĂLĂNESCU4 The paper provides a novel physico-mathematical model able to estimate the maximum performances of a hot air Ericsson-type engine - which is capable to run on renewable energy, such as solar energy, geothermal energy or biomass. The computing program based on this new model allows to study the influences of the main parameters over the engine performances and to optimize their values. Keywords: Ericsson-type engine, renewable energy, theoretical model, maximum performances. 1. Introduction In the last decades we witnessed an extraordinary development of numerous engines and devices capable of transforming heat into work [1]. The field of the “unconventional” engines has risen again into the attention of the researchers and of the investors. Several former abandoned or marginal technical solutions of hot air engines were reanalyzed by researchers - as the Ericsson-type reciprocating engines [2], Stirling engines or Stirling-related engines [1], [3] and the Vuilleumier machine. The Ericsson-type hot air engine is an external combustion heat engine with pistons (usually, with pistons with reciprocating movement) and with valves. An Ericsson-type engine functional unit comprises two pistons. The compression process takes place inside a compression cylinder, and the expansion process takes place inside an expansion cylinder. Heat is added to the cycle inside a heater. Sometimes a heat recuperator or regenerator is used to recover energy from the exhaust gases, fig.
    [Show full text]
  • Problem 3.130
    PROBLEM 3.130 PROBLEM 3.117 3 o 2 As shown in Fig. P3.117, 20 ft of air at T1 = 600 R, 100 lbf/in. undergoes a polytropic expansion to a final pressure of 51.4 lbf/in.2 The process follows pV1.2 = constant. The work is W = 194.34 Btu. Assuming ideal gas behavior for the air, and neglecting kinetic and potential energy effects, determine (a) the mass of air, in lb, and the final temperature, in oR. (b) the heat transfer, in Btu. KNOWN: Air undergoes a polytropic process in a piston-cylinder assembly. The work is known. FIND: Determine the mass of air, the final temperature, and the heat transfer. SCHEMATIC AND GIVEN DATA: o T1 = 600 R Q 2 p1 = 100 lbf/in. 3 V1 = 20 ft Air 2 P2 = 51.4 lbf/in. W = 194.34 Btu 1.2 pV = constant pv1.2 = constant p 1 100 . T1 ENGINEERING MODEL: 1. The air is a closed system. 2. Volume change is the only work mode. 3. The process is 1.2 2 polytropic, with pV = constant and W = 194.34 Btu. 51.4 . T2 4. Kinetic and potential energy effects can be neglected. ANALYSIS: (a) The mass is determined using the ideal gas equation of state. v m = = = 9.00 lb 1.2 To get the final temperature, we use the polytropic process, pV = constant, to evaluate V2 as follows. 3 3 V2 = = (20 ft ) = 34.83 ft Now PROBLEM 3.117 (CONTINUED) o T2 = = = 537 R Alternative solution for T2 1.2 The work for the polytropic process can be evaluated using W = .
    [Show full text]
  • The First Law of Thermodynamics: Closed Systems Heat Transfer
    The First Law of Thermodynamics: Closed Systems The first law of thermodynamics can be simply stated as follows: during an interaction between a system and its surroundings, the amount of energy gained by the system must be exactly equal to the amount of energy lost by the surroundings. A closed system can exchange energy with its surroundings through heat and work transfer. In other words, work and heat are the forms that energy can be transferred across the system boundary. Based on kinetic theory, heat is defined as the energy associated with the random motions of atoms and molecules. Heat Transfer Heat is defined as the form of energy that is transferred between two systems by virtue of a temperature difference. Note: there cannot be any heat transfer between two systems that are at the same temperature. Note: It is the thermal (internal) energy that can be stored in a system. Heat is a form of energy in transition and as a result can only be identified at the system boundary. Heat has energy units kJ (or BTU). Rate of heat transfer is the amount of heat transferred per unit time. Heat is a directional (or vector) quantity; thus, it has magnitude, direction and point of action. Notation: – Q (kJ) amount of heat transfer – Q° (kW) rate of heat transfer (power) – q (kJ/kg) ‐ heat transfer per unit mass – q° (kW/kg) ‐ power per unit mass Sign convention: Heat Transfer to a system is positive, and heat transfer from a system is negative. It means any heat transfer that increases the energy of a system is positive, and heat transfer that decreases the energy of a system is negative.
    [Show full text]
  • On the Calculation of the Effective Polytropic Index in Space Plasmas
    entropy Article On the Calculation of the Effective Polytropic Index in Space Plasmas Georgios Nicolaou 1,* , George Livadiotis 2 and Robert T. Wicks 1 1 Department of Space and Climate Physics, Mullard Space Science Laboratory, University College London, Dorking, Surrey RH5 6NT, UK; [email protected] 2 Southwest Research Institute, San Antonio, TX 78238, USA; [email protected] * Correspondence: [email protected] Received: 25 September 2019; Accepted: 10 October 2019; Published: 12 October 2019 Abstract: The polytropic index of space plasmas is typically determined from the relationship between the measured plasma density and temperature. In this study, we quantify the errors in the determination of the polytropic index, due to uncertainty in the analyzed measurements. We model the plasma density and temperature measurements for a certain polytropic index, and then, we apply the standard analysis to derive the polytropic index. We explore the accuracy of the derived polytropic index for a range of uncertainties in the modeled density and temperature and repeat for various polytropic indices. Our analysis shows that the uncertainties in the plasma density introduce a systematic error in the determination of the polytropic index which can lead to artificial isothermal relations, while the uncertainties in the plasma temperature increase the statistical error of the calculated polytropic index value. We analyze Wind spacecraft observations of the solar wind protons and we derive the polytropic index in selected intervals over 2002. The derived polytropic index is affected by the plasma measurement uncertainties, in a similar way as predicted by our model. Finally, we suggest a new data-analysis approach, based on a physical constraint, that reduces the amount of erroneous derivations.
    [Show full text]
  • Air Standard Cycles
    1 Thermodynamic analysis of IC Engine Air-Standard Cycle Table of Contents 2 Introduction Air Standard Cycles Otto cycle Thermodynamic Analysis of Air-Standard Otto Cycle Diesel Cycle Thermodynamic Analysis of Air-Standard Diesel Cycle Dual Cycle Thermodynamic Analysis of Air-Standard Dual Cycle Comparison of OTTO,DIESEL, and DUAL Cycles Atkinson Cycle Miller Cycle Lenoir Cycle Thermodynamic Analysis of Air-Standard Lenoir Cycle Introduction 3 The Three Thermodynamic Analysis of IC Engines are I. Ideal Gas Cycle (Air Standard Cycle) Idealized processes Idealize working Fluid II. Fuel-Air Cycle Idealized Processes Accurate Working Fluid Model III. Actual Engine Cycle Accurate Models of Processes Accurate Working Fluid Model Introduction 4 The operating cycle of an IC engine can be broken down into a sequence of separate processes Intake, Compression, Combustion, Expansion and Exhaust. Actual IC Engine does not operate on ideal thermodynamic cycle that are operated on open cycle. The accurate analysis of IC engine processes is very complicated, to understand it well, it is advantageous to analyze the performance of an Idealized closed cycle Air Standard Cycles 5 Air-Standard cycle differs from the actual by the following 1. The gas mixture in the cylinder is treated as air for the entire cycle, and property values of air are used in the analysis. 2. The real open cycle is changed into a closed cycle by assuming that the gases being exhausted are fed back into the intake system. 3. The combustion process is replaced with a heat addition term Qin of equal energy value Air standard cycles 6 4.
    [Show full text]