SI Unit Exercises
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

M Motion Intervention Booklet.Pdf (810.7KB)
Motion Intervention Booklet 1 Random uncertainties have no pattern. They can cause a reading to be higher or lower than the “true value”. Systematic uncertainties have a pattern. They cause readings to be consistently too high or consistently too low. 2 The uncertainty in repeat readings is found from “half the range” and is given to 1 significant figure. Time / s Trial 1 Trial 2 Trial 3 Mean 1.23 1.20 1.28 Mean time = 1.23 + 1.20 + 1.28 = 1.23666666 => 1.24 (original data is to 2dp, so 3 the mean is to 2 dp as well) Range = 1.20 1.28. Uncertainty is ½ × (1.28 – 1.20) = ½ × 0.08 = ± 0.04 s 3 The speed at which a person can walk, run or cycle depends on many factors including: age, terrain, fitness and distance travelled. The speed of a moving object usually changes while it’s moving. Typical values for speeds may be taken as: walking: 1.5 m/s running: 3 m/s cycling: 6 m/s sound in air: 330 m/s 4 Scalar quantities have magnitude only. Speed is a scaler, eg speed = 30 m/s. Vector quantities have magnitude and direction. Velocity is a vector, eg velocity = 30 m/s north. Distance is how far something moves, it doesn’t involve direction. The displacement at a point is how far something is from the start point, in a straight line, including the direction. It doesn’t make any difference how far the object has moved in order to get to that point. -

Measurement-Resource-Book-1.Pdf
First Steps in Mathematics Measurement Understand Units and Resource Book 1 Direct Measure Improving the mathematics outcomes of students FSIM010 | First Steps in Mathematics: Measurement Book 1 © Western Australian Minister for Education 2013. Published by Pearson Canada Inc. First Steps in Mathematics: Measurement Resource Book 1 Understand Units and Direct Measure © Western Australian Minister for Education 2013 Published in Canada by Pearson Canada Inc. 26 Prince Andrew Place Don Mills, ON M3C 2T8 Text by Sue Willis with Wendy Devlin, Lorraine Jacob, Beth Powell, Dianne Tomazos, and Kaye Treacy for STEPS Professional Development on behalf of the Department of Education and Training, Western Australia. Photos: Ray Boudreau Illustrations: Neil Curtis, Vesna Krstanovich and David Cheung ISBN-13: 978-0-13-188205-8 ISBN-10: 0-13-188205-8 Publisher: Debbie Davidson Director, Pearson Professional Learning: Terry (Theresa) Nikkel Research and Communications Manager: Chris Allen Canadian Edition Consultants: Craig Featherstone, David McKillop, Barry Onslow Development House: Pronk&Associates Project Coordinator: Joanne Close Art Direction: Jennifer Stimson and Zena Denchik Design: Jennifer Stimson and David Cheung Page Layout: Computer Composition of Canada Inc. FSIM010 | First Steps in Mathematics: Measurement Book 1 © Western Australian Minister for Education 2013. Published by Pearson Canada Inc. Diagnostic Map: Measurement Matching and Emergent Phase Comparing Phase Quantifying Phase Most students will enter the Matching and Most students -

CAR-ANS Part 5 Governing Units of Measurement to Be Used in Air and Ground Operations
CIVIL AVIATION REGULATIONS AIR NAVIGATION SERVICES Part 5 Governing UNITS OF MEASUREMENT TO BE USED IN AIR AND GROUND OPERATIONS CIVIL AVIATION AUTHORITY OF THE PHILIPPINES Old MIA Road, Pasay City1301 Metro Manila UNCOTROLLED COPY INTENTIONALLY LEFT BLANK UNCOTROLLED COPY CAR-ANS PART 5 Republic of the Philippines CIVIL AVIATION REGULATIONS AIR NAVIGATION SERVICES (CAR-ANS) Part 5 UNITS OF MEASUREMENTS TO BE USED IN AIR AND GROUND OPERATIONS 22 APRIL 2016 EFFECTIVITY Part 5 of the Civil Aviation Regulations-Air Navigation Services are issued under the authority of Republic Act 9497 and shall take effect upon approval of the Board of Directors of the CAAP. APPROVED BY: LT GEN WILLIAM K HOTCHKISS III AFP (RET) DATE Director General Civil Aviation Authority of the Philippines Issue 2 15-i 16 May 2016 UNCOTROLLED COPY CAR-ANS PART 5 FOREWORD This Civil Aviation Regulations-Air Navigation Services (CAR-ANS) Part 5 was formulated and issued by the Civil Aviation Authority of the Philippines (CAAP), prescribing the standards and recommended practices for units of measurements to be used in air and ground operations within the territory of the Republic of the Philippines. This Civil Aviation Regulations-Air Navigation Services (CAR-ANS) Part 5 was developed based on the Standards and Recommended Practices prescribed by the International Civil Aviation Organization (ICAO) as contained in Annex 5 which was first adopted by the council on 16 April 1948 pursuant to the provisions of Article 37 of the Convention of International Civil Aviation (Chicago 1944), and consequently became applicable on 1 January 1949. The provisions contained herein are issued by authority of the Director General of the Civil Aviation Authority of the Philippines and will be complied with by all concerned. -

General Principles of Airborne Gravity Gradiometers for Mineral Exploration, in R.J.L
Geoscience Australia Record 2004/18 Airborne Gravity 2004 Abstracts from the ASEG-PESA Airborne Gravity 2004 Workshop Edited by Richard Lane Department of Industry, Tourism & Resources Minister for Industry, Tourism & Resources: The Hon. Ian Macfarlane, MP Parliamentary Secretary: The Hon. Warren Entsch, MP Secretary: Mark Paterson Geoscience Australia Chief Executive Officer: Neil Williams © Commonwealth of Australia 2004 This work is copyright. Apart from any fair dealings for the purposes of study, research, criticism or review, as permitted under the Copyright Act, no part may be reproduced by any process without written permission. Inquiries should be directed to the Communications Unit, Geoscience Australia, GPO Box 378, Canberra City, ACT, 2601 ISSN: 1448-2177 ISBN: 1 920871 13 6 GeoCat no. 61129 Bibliographic Reference: a) For the entire publication Lane, R.J.L., editor, 2004, Airborne Gravity 2004 – Abstracts from the ASEG-PESA Airborne Gravity 2004 Workshop: Geoscience Australia Record 2004/18. b) For an individual paper van Kann, F., 2004, Requirements and general principles of airborne gravity gradiometers for mineral exploration, in R.J.L. Lane, editor, Airborne Gravity 2004 - Abstracts from the ASEG-PESA Airborne Gravity 2004 Workshop: Geoscience Australia Record 2004/18, 1-5. Geoscience Australia has tried to make the information in this product as accurate as possible. However, it does not guarantee that the information is totally accurate or complete. THEREFORE, YOU SHOULD NOT RELY SOLELY ON THIS INFORMATION WHEN MAKING A COMMERCIAL DECISION. ii Contents “Airborne Gravity 2004 Workshop” Record R.J.L. Lane, M.H. Dransfield, D. Robson, R.J. Smith and G. Walker…………………………………..v Requirements and general principles of airborne gravity gradiometers for mineral exploration F. -

CAR-ANS PART 05 Issue No. 2 Units of Measurement to Be Used In
CIVIL AVIATION REGULATIONS AIR NAVIGATION SERVICES Part 5 Governing UNITS OF MEASUREMENT TO BE USED IN AIR AND GROUND OPERATIONS CIVIL AVIATION AUTHORITY OF THE PHILIPPINES Old MIA Road, Pasay City1301 Metro Manila INTENTIONALLY LEFT BLANK CAR-ANS PART 5 Republic of the Philippines CIVIL AVIATION REGULATIONS AIR NAVIGATION SERVICES (CAR-ANS) Part 5 UNITS OF MEASUREMENTS TO BE USED IN AIR AND GROUND OPERATIONS 22 APRIL 2016 EFFECTIVITY Part 5 of the Civil Aviation Regulations-Air Navigation Services are issued under the authority of Republic Act 9497 and shall take effect upon approval of the Board of Directors of the CAAP. APPROVED BY: LT GEN WILLIAM K HOTCHKISS III AFP (RET) DATE Director General Civil Aviation Authority of the Philippines Issue 2 15-i 16 May 2016 CAR-ANS PART 5 FOREWORD This Civil Aviation Regulations-Air Navigation Services (CAR-ANS) Part 5 was formulated and issued by the Civil Aviation Authority of the Philippines (CAAP), prescribing the standards and recommended practices for units of measurements to be used in air and ground operations within the territory of the Republic of the Philippines. This Civil Aviation Regulations-Air Navigation Services (CAR-ANS) Part 5 was developed based on the Standards and Recommended Practices prescribed by the International Civil Aviation Organization (ICAO) as contained in Annex 5 which was first adopted by the council on 16 April 1948 pursuant to the provisions of Article 37 of the Convention of International Civil Aviation (Chicago 1944), and consequently became applicable on 1 January 1949. The provisions contained herein are issued by authority of the Director General of the Civil Aviation Authority of the Philippines and will be complied with by all concerned. -

Orders of Magnitude (Length) - Wikipedia
03/08/2018 Orders of magnitude (length) - Wikipedia Orders of magnitude (length) The following are examples of orders of magnitude for different lengths. Contents Overview Detailed list Subatomic Atomic to cellular Cellular to human scale Human to astronomical scale Astronomical less than 10 yoctometres 10 yoctometres 100 yoctometres 1 zeptometre 10 zeptometres 100 zeptometres 1 attometre 10 attometres 100 attometres 1 femtometre 10 femtometres 100 femtometres 1 picometre 10 picometres 100 picometres 1 nanometre 10 nanometres 100 nanometres 1 micrometre 10 micrometres 100 micrometres 1 millimetre 1 centimetre 1 decimetre Conversions Wavelengths Human-defined scales and structures Nature Astronomical 1 metre Conversions https://en.wikipedia.org/wiki/Orders_of_magnitude_(length) 1/44 03/08/2018 Orders of magnitude (length) - Wikipedia Human-defined scales and structures Sports Nature Astronomical 1 decametre Conversions Human-defined scales and structures Sports Nature Astronomical 1 hectometre Conversions Human-defined scales and structures Sports Nature Astronomical 1 kilometre Conversions Human-defined scales and structures Geographical Astronomical 10 kilometres Conversions Sports Human-defined scales and structures Geographical Astronomical 100 kilometres Conversions Human-defined scales and structures Geographical Astronomical 1 megametre Conversions Human-defined scales and structures Sports Geographical Astronomical 10 megametres Conversions Human-defined scales and structures Geographical Astronomical 100 megametres 1 gigametre -
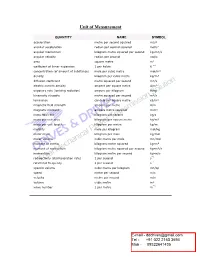
Unit of Measurement
Unit of Measurement QUANTITY NAME SYMBOL acceleration metre per second squared m/s² angular acceleration radian per second squared rad/s² angular momentum kilogram metre squared per second kg•m²/s angular velocity radian per second rad/s area square metre m² cœfficient of linear expansion 1 per kelvin K ¯¹ concentration (of amount of substance) mole per cubic metre mol/m³ density kilogram per cubic metre kg/m³ diffusion cœfficient metre squared per second m²/s electric current density ampere per square metre A/m² exposure rate (ionising radiation) ampere per kilogram A/kg kinematic viscosity metre squared per second m²/s luminance candela per square metre cd/m² magnetic field strength ampere per metre A/m magnetic moment ampere metre squared A•m² mass flow rate kilogram per second kg/s mass per unit area kilogram per square metre kg/m² mass per unit length kilogram per metre kg/m molality mole per kilogram mol/kg molar mass kilogram per mole kg/mol molar volume cubic metre per mole m³/mol moment of inertia kilogram metre squared kg•m² moment of momentum kilogram metre squared per second kg•m²/s momentum kilogram metre per second kg•m/s radioactivity (disintergration rate) 1 per second s¯¹ rotational frequency 1 per second s¯¹ specific volume cubic metre per kilogram m³/kg speed metre per second m/s velocity metre per second m/s volume cubic metre m³ wave number 1 per metre m¯¹ SI units and Additional QUANTITY NAME SYMBOL units absorbed dose joule per kilogram J/kg m²•s¯² watt per meter squared coefficient of heat transfer W/m²•K kg•s¯³•K¯¹ -

6411 Measure Unit Qualifier Indication of the Unit of Measurement in Which Weight (Mass), Capacity, Length, Area, Volume Or Other Quantity Is Expressed
Code list 6411 Standard: UN D.96B S3 6411 Measure unit qualifier Indication of the unit of measurement in which weight (mass), capacity, length, area, volume or other quantity is expressed. Note: See UN/ECE Recommendation 20. 04 small spray 05 lift 08 heat lot 10 group 11 outfit 13 ration 14 shot 15 stick 16 hundred fifteen kg drum 17 hundred lb drum 18 fiftyfive gallon (US) drum 19 tank truck 20 twenty foot container 21 forty foot container 22 decilitre per gram 23 gram per cubic centimetre 24 theoretical pound 25 gram per square centimetre 26 actual ton 27 theoretical ton 28 kilogram per square metre 29 pound per thousand square feet 30 horse power day per air dry metric ton 31 catch weight 32 kilogram per air dry metric ton 33 kilopascal square metres per gram 34 kilopascals per millimetre 35 millilitres per square centimetre second 36 cubic feet per minute per square foot 37 ounce per square foot 38 ounces per square foot per 0,01 inch 40 millilitre per second 41 millilitre per minute 43 super bulk bag 44 fivehundred kg bulk bag 45 threehundred kg bulk bag 46 fifty lb bulk bag 47 fifty lb bag 48 bulk car load 53 theoretical kilograms Printed by GEFEG EDIFIX® Print date: 26/09/2001 Page: 1 Code list 6411 Standard: UN D.96B S3 54 theoretical tonne 56 sitas 57 mesh 58 net kilogram 59 part per million 60 percent weight 61 part per billion (US) 62 percent per 1000 hour 63 failure rate in time 64 pound per square inch, gauge 66 oersted 69 test specific scale 71 volt ampere per pound 72 watt per pound 73 ampere tum per centimetre 74 millipascal -

SI QUICK REFERENCE GUIDE: International System of Units (SI) the Modernized Metric System*
SI QUICK REFERENCE GUIDE: International System of Units (SI) The Modernized Metric System* UNITS The International System of Units (SI) is based on seven fundamental (base) units: Base Units Quantity Name Symbol length metre m mass kilogram kg time second s electric current ampere A thermodynamic temperature kelvin K amount of substance mole mol luminous intensity candela cd and a number of derived units which are combinations of base units and which may have special names and symbols: Examples of Derived Units Quantity Expression Name Symbol acceleration angular rad/s2 linear m/s2 angle plane dimensionless radian rad solid dimensionless steradian sr area m2 Celsius temperature K degree Celsius °C density heat flux W/ m2 mass kg/m3 current A/m2 energy, enthalpy work, heat N • m joule J specific J/ kg entropy heat capacity J/ K specific J/ (kg•K) flow, mass kg/s flow, volume m3/s force kg • m/s2 newton N frequency periodic 1/s hertz Hz rotating rev/s inductance Wb/A henry H magnetic flux V • s weber Wb mass flow kg/s moment of a force N • m potential,electric W/A volt V power, radiant flux J/s watt W pressure, stress N/m2 pascal Pa resistance, electric V/A ohm Ω thermal conductivity W/(m • K) velocity angular rad/s linear m/s viscosity dynamic (absolute)(µ)Pa• s kinematic (ν)m2/s volume m3 volume, specific m3/kg *For complete information see IEEE/ASTM SI-10. SI QUICK REFERENCE GUIDE SYMBOLS Symbol Name Quantity Formula A ampere electric current base unit Bq becquerel activity (of a radio nuclide) 1/s C coulomb electric charge A • s °C -

Units of Measure Used in International Trade Page 1/57 Annex II (Informative) Units of Measure: Code Elements Listed by Name
Annex II (Informative) Units of Measure: Code elements listed by name The table column titled “Level/Category” identifies the normative or informative relevance of the unit: level 1 – normative = SI normative units, standard and commonly used multiples level 2 – normative equivalent = SI normative equivalent units (UK, US, etc.) and commonly used multiples level 3 – informative = Units of count and other units of measure (invariably with no comprehensive conversion factor to SI) The code elements for units of packaging are specified in UN/ECE Recommendation No. 21 (Codes for types of cargo, packages and packaging materials). See note at the end of this Annex). ST Name Level/ Representation symbol Conversion factor to SI Common Description Category Code D 15 °C calorie 2 cal₁₅ 4,185 5 J A1 + 8-part cloud cover 3.9 A59 A unit of count defining the number of eighth-parts as a measure of the celestial dome cloud coverage. | access line 3.5 AL A unit of count defining the number of telephone access lines. acre 2 acre 4 046,856 m² ACR + active unit 3.9 E25 A unit of count defining the number of active units within a substance. + activity 3.2 ACT A unit of count defining the number of activities (activity: a unit of work or action). X actual ton 3.1 26 | additional minute 3.5 AH A unit of time defining the number of minutes in addition to the referenced minutes. | air dry metric ton 3.1 MD A unit of count defining the number of metric tons of a product, disregarding the water content of the product. -

Beyond the Metre (Part II)
Iowa Science Teachers Journal Volume 17 Number 2 Article 10 1980 Beyond the Metre (Part II) Richard S. Thompkins Mississippi Bend Area Education Agency Vincent N. Lunetta University of Iowa Follow this and additional works at: https://scholarworks.uni.edu/istj Part of the Science and Mathematics Education Commons Let us know how access to this document benefits ouy Copyright © Copyright 1980 by the Iowa Academy of Science Recommended Citation Thompkins, Richard S. and Lunetta, Vincent N. (1980) "Beyond the Metre (Part II)," Iowa Science Teachers Journal: Vol. 17 : No. 2 , Article 10. Available at: https://scholarworks.uni.edu/istj/vol17/iss2/10 This Article is brought to you for free and open access by the Iowa Academy of Science at UNI ScholarWorks. It has been accepted for inclusion in Iowa Science Teachers Journal by an authorized editor of UNI ScholarWorks. For more information, please contact [email protected]. BEYOND THE METRE (Part II) Richard S. Tompkins Metric Education Consultant Mississippi Bend Area Education Agency 2604 West Locust Street Davenport, Iowa 52804 Vincent N. Lunetta Associate Professor of Science Education University of Iowa Iowa City, Iowa 52242 Introduction This article is the second in a series discussing the wide spectrum of metric units. The first article dealt with some general aspects of the International System of Units (SI) and then went on to consider the metre, square metre, cubic metre and second. This article describes the SI unit of mass, and how units for velocity and acceleration are built using physical laws. The Metre Per Second (mis) Speed is usually represented in terms of a distance traveled during some time interval. -

Not Made to Measure
Made in Britain: Not made to measure. Ronnie Cohen © 2011 Ronnie Cohen. All rights reserved. 1 Table of Contents Foreword...............................................................................................................................................5 Introduction..........................................................................................................................................6 Central Role of Measurement in Daily Life.........................................................................................7 Why Measurement Matters..................................................................................................................8 Quest for Honest Measurements since Ancient Times.........................................................................9 Measurement Facts: Did you know that....?.......................................................................................10 Description of the British Imperial System........................................................................................11 Introduction to the British Imperial System..............................................................................11 Units of Length..........................................................................................................................11 Units of Area.............................................................................................................................11 Units of Volume........................................................................................................................12