DOCSLIB.ORG

Atmosphere and Ocean Differences

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Atmosphere and Ocean Differences Atmosphere and ocean differences Lesson 2 Atmosphere & ocean properties: Fluids are physically different Water is incompressible (atm is assumed equations of state and density incompressible for many applications) Ocean has no analogy for “latent heat” source that atm has Review: differences b/t ocean & Oceans are laterally bounded (by land) Atm circulation largely forced by convection – heating atmosphere, equations of state from below for atmosphere & ocean Ocean circulation forced by convection – heat loss from above – and by wind stress (no analogy in atm) Density Equation of state Density ( ρ) is defined as the mass per unit volume: The equation of state - The functional relationship between the absolute pressure, specific volume and temperature for a ρ = mass Volume homogenous substance. With units: g or kg General form: cm 3 m3 . Density is related to the specific volume, α, which is the . f (p,α,T ) = 0 volume per unit mass α = 1 ρ 3 m3 With units: cm or g kg 1 Ideal Gas law – Moist Ideal Gas law atmosphere The equation of state – For relatively small pressure values (on the order of (1 atm)), there exists an analytic relationship for the Due to Dalton’s law of partial pressures, we can express an ideal equation of state: gas law for the molecular constituents of the atmosphere p = ρRT = ρ * R * p Rd T R = Where m And m is the molecular mass with units grams/mole = × 2 Joules Where Rd .2 8705 10 is the ideal gas constant for dry air kg ⋅o Kelvin . Joules . And R* = .8 3143 ×10 3 is the ideal gas constant. o Kelvin ⋅ kg ⋅ mole T* is the virtual temperature and is defined as the temperature a parcel of dry air would have if its pressure and density were those of the parcel of This equation is only valid under the conditions that: moist air. If W is the mixing ratio in units of gm/kg then 1. Molecules exhibit no potential forces between each other. They only W interact through elastics collisions like billiard balls. T * ≈ T + 2. Molecules occupy no volume. They are all treated as “point” 6 masses Equation of state for the ocean General properties of ocean Clearly, the requirements of the ideal gas law break down in Seawater is nearly incompressible (more than the ocean and therefore we are stuck with the general form of the equation of state: fresh water or air), thus seawater density depends (mostly) on salinity & temperature f (p,α,T ) = 0 More dense Less dense In practice, we are interested in examining how the density . (specific volume) of the ocean varies with Pressure, Temperature and Salinity. Cold water Warm water Density increases with a(n): Salty water Fresh(er) water - increase in Salinity and Pressure Density units in kg m -3 - decrease in Temperature 2 3. (from Pinet, 1998) What are factors that control the growth and structure of the Thermocline? 4 (NORTHERN HEMISPHERE) (from Pinet, 1998) SALINITY General definition - The mass of salt per unit mass of seawater - measured in parts per thousand– It is very difficult to actually find the amount of salt or the amount of water at a given Temperature and pressure – Evaporation alone is not sufficient. Practical Salinity : Salinity measured in accordance with the Practical Salinity Scale (conductivity scale as compared to a standard KCL solution) and has Practical Salinity units (PSUs). 4 (NORTHERN HEMISPHERE) (from Pinet, 1998) 3 Major Constituents high temperate subtropical The concentrations of these 7. major constituents are conservative. They are (from Pinet, 1998) unaffected by most biological and chemical processes. What is the “halocline”? What factors control the growth and structure of the halocline? 11. (from Pinet, 1998) (from the Navy Coastal Ocean Model) Why is the Atlantic saltier (at the surface) than the other global oceans? 4 Effect of pressure on density In-situ versus laboratory θθθ = T − ∫ Γdp Theoretical analysis of the ocean is important but is of little use o ∂T g − C without the experimental results to accompany it. Γ = = ≈ 1− 2 ×10 4 ∂ p Cp db There are many ways of obtaining the thermodynamics properties of Data off C ≈ 4 ×10 4 J /( kg oC) the ocean. These can broken into two main categories: Antarctica p In-situ – measuring the quantities of interest at depth in the ocean. Γ is the adiabatic Often, the use of a CTD can be used for these type measurements. lapse rate Laboratory – Measuring the properties of interest by taking a sample . at depth and bringing it to the surface. One must then account for variations in pressure and, to a lesser degree, temperature, in ~0.1º change at 1000 m transporting the fluid parcel. Many chemical properties of sea-water potential in-situ require this type of measurement. – ~0.3º change at 3000 m One must be careful though since neglect of pressure may mislead the observer into indications of an instability when actually does not exist. Γ can also be obtained from Unesco North Atlantic Deep Water (with higher potential density) over Technical Papers in Marine Science # 44 by Antarctic Bottom Water (with lesser potential density) Fofonoff and Millard, Unesco 1983 Ocean density representation Ocean density representation Given that we know density depends on salinity, temperature and pressure, we can approximate density as a linear function of its state variables using a Density is actually a non-linear function of T,S and p so we must use different techniques to get an accurate representation of density over Taylor series. If we expand about reference values, To, So and po we obtain a wide range of state variable values ρ( ) ≈ ρ ( −α ( − )+ β ( − ) + ( − )) T, S, p o 1 T T To S S So K p po The international equation of state for seawater is a widely accepted Where empirical technique to obtain accurate values of density to order 10 -5. ∂ρ α = − 1 - Thermal expansion coefficient T ρ ∂ . T . The international equation of state for seawater is not static (fixed), ∂ρ and note that the Intergovernmental Oceanographic Commission has β = 1 S - Haline contraction coefficient approved a modification, TEOS-10 http://www.teos-10.org/ ρ ∂S 1 ∂ρ K = = An amazingly detailed (179 pg) brief is hosted by the Australian government ρ ∂ - Isothermal compressibility coefficient p (Commonwealth Scientific and Industrial Research Organisation) at: http://www.marine.csiro.au/~jackett/TEOS-10/TEOS-10_Manual_08Jan2010.pdf The above representation is only useful locally (with little change in the domain or parameters) 5 International equation of state International equation of state for seawater for seawater The international equation of state for seawater calculates density by finding the secant bulk modulus, K, which is the slope of a segment on Solving for density in the previous equation we obtain a graph of density versus fractional rate of change of volume. α ρ Its value is K = o p = p ρ ( ) α −α ρ − ρ o S,T, po o o ρ()S,T, p = p 1− K()S,T, p p . K and ρ =0 are then empirically fit to different values of salinity, α ρ ο K = o p = p ρ α −α ρ − ρ temperature and pressure. The accepted expansion of K and ο are . o o α − α α −α p = ,0 o = 0 o o α α o o International equation of state Representing the density of for seawater seawater K(S,T, p) = There are other more recent techniques for finding the density of ρ( ) = 19652 21. S,T 0, seawater. −2 +148 .4206 T − .2 327105 T 2 999 .842594 + .6 793952 ×10 T − − + .1 360477 ×10 2 T 3 − .5 155288 ×10 5 T 4 − .9 095290 ×10 −3T 2 + .1 001685 ×10 −4 T 3 Some recent approaches are by McDougall et al (2002) or Feistel −3 + .3 239908 p + .1 43713 ×10 Tp − − (2003) − .1 120083 ×10 6 T 4 + .6 536332 ×10 9 T 5 + .1 16092 ×10 −4 T 2 p − .5 77905 ×10 −7 T 3 p + × −1 − × −3 + .8 50935 ×10 −5 p 2 − .6 12293 ×10 −6 Tp 2 .8 24493 10 S .4 0899 10 TS McDougall T.J., Jackett D. R., Wright D. G., Feistel R., 2002, Accurate −8 2 2 −5 2 −7 3 . + .5 2787 ×10 T p + .7 6438 ×10 T S − .8 2467 ×10 T S . and computationally efficient formulae for potential temperature and + − − − density. J. Atmos. Ocean. Tech., 20 , 730-741 54 .6746 S .0 603459 TS + .5 3875 ×10 9 T 4 S − .5 72466 ×10 3 S 2/3 + × −2 2 − × −5 3 .1 09987 10 T S .6 1670 10 T S −4 2/3 −6 2 2/3 − − + .1 0227 ×10 TS − .1 6546 ×10 T S + .7 944 ×10 2 S 2/3 + .1 6483 ×10 2 TS /3 2 Feistel R., 2003. A new extended thermodynamic potential of −4 2 − .5 3009 ×10 −4 T 2 S /3 2 + .2 2838 ×10 −3 pS + 4.8314 ×10 S seawater. Prog. Oceanography , 36 , 249-347. − .1 0981 ×10 −5 TpS − .1 6078 ×10 −6 T 2 pS + .1 91075 ×10 −4 pS 2/3 − .9 9348 ×10 −7 p 2 S + .2 0816 ×10 −8 Tp 2 S + .9 1697 ×10 −10 T 2 p 2 S 6 Tables A good java program that allows use to find the thermodynamic properties of the ocean is found . here . 7.
Load more

Recommended publications
  • Thermodynamics Notes
    Thermodynamics Notes Steven K. Krueger Department of Atmospheric Sciences, University of Utah August 2020 Contents 1 Introduction 1 1.1 What is thermodynamics? . .1 1.2 The atmosphere . .1 2 The Equation of State 1 2.1 State variables . .1 2.2 Charles' Law and absolute temperature . .2 2.3 Boyle's Law . .3 2.4 Equation of state of an ideal gas . .3 2.5 Mixtures of gases . .4 2.6 Ideal gas law: molecular viewpoint . .6 3 Conservation of Energy 8 3.1 Conservation of energy in mechanics . .8 3.2 Conservation of energy: A system of point masses . .8 3.3 Kinetic energy exchange in molecular collisions . .9 3.4 Working and Heating . .9 4 The Principles of Thermodynamics 11 4.1 Conservation of energy and the first law of thermodynamics . 11 4.1.1 Conservation of energy . 11 4.1.2 The first law of thermodynamics . 11 4.1.3 Work . 12 4.1.4 Energy transferred by heating . 13 4.2 Quantity of energy transferred by heating . 14 4.3 The first law of thermodynamics for an ideal gas . 15 4.4 Applications of the first law . 16 4.4.1 Isothermal process . 16 4.4.2 Isobaric process . 17 4.4.3 Isosteric process . 18 4.5 Adiabatic processes . 18 5 The Thermodynamics of Water Vapor and Moist Air 21 5.1 Thermal properties of water substance . 21 5.2 Equation of state of moist air . 21 5.3 Mixing ratio . 22 5.4 Moisture variables . 22 5.5 Changes of phase and latent heats .
    [Show full text]
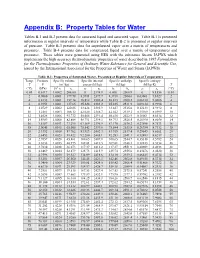
  • Appendix B: Property Tables for Water
    Appendix B: Property Tables for Water Tables B-1 and B-2 present data for saturated liquid and saturated vapor. Table B-1 is presented information at regular intervals of temperature while Table B-2 is presented at regular intervals of pressure. Table B-3 presents data for superheated vapor over a matrix of temperatures and pressures. Table B-4 presents data for compressed liquid over a matrix of temperatures and pressures. These tables were generated using EES with the substance Steam_IAPWS which implements the high accuracy thermodynamic properties of water described in 1995 Formulation for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use, issued by the International Associated for the Properties of Water and Steam (IAPWS). Table B-1: Properties of Saturated Water, Presented at Regular Intervals of Temperature Temp. Pressure Specific volume Specific internal Specific enthalpy Specific entropy T P (m3/kg) energy (kJ/kg) (kJ/kg) (kJ/kg-K) T 3 (°C) (kPa) 10 vf vg uf ug hf hg sf sg (°C) 0.01 0.6117 1.0002 206.00 0 2374.9 0.000 2500.9 0 9.1556 0.01 2 0.7060 1.0001 179.78 8.3911 2377.7 8.3918 2504.6 0.03061 9.1027 2 4 0.8135 1.0001 157.14 16.812 2380.4 16.813 2508.2 0.06110 9.0506 4 6 0.9353 1.0001 137.65 25.224 2383.2 25.225 2511.9 0.09134 8.9994 6 8 1.0729 1.0002 120.85 33.626 2385.9 33.627 2515.6 0.12133 8.9492 8 10 1.2281 1.0003 106.32 42.020 2388.7 42.022 2519.2 0.15109 8.8999 10 12 1.4028 1.0006 93.732 50.408 2391.4 50.410 2522.9 0.18061 8.8514 12 14 1.5989 1.0008 82.804 58.791 2394.1 58.793 2526.5
    [Show full text]
  • Equation of State of an Ideal Gas
    ASME231 Atmospheric Thermodynamics NC A&T State U Department of Physics Dr. Yuh-Lang Lin http://mesolab.org [email protected] Lecture 3: Equation of State of an Ideal Gas As mentioned earlier, the state of a system is the condition of the system (or part of the system) at an instant of time measured by its properties. Those properties are called state variables, such as T, p, and V. The equation which relates T, p, and V is called equation of state. Since they are related by the equation of state, only two of them are independent. Thus, all the other thermodynamic properties will depend on the state defined by two independent variables by state functions. PVT system: The simplest thermodynamic system consists of a fixed mass of a fluid uninfluenced by chemical reactions or external fields. Such a system can be described by the pressure, volume and temperature, which are related by an equation of state f (p, V, T) = 0, (2.1) 1 where only two of them are independent. From physical experiments, the equation of state for an ideal gas, which is defined as a hypothetical gas whose molecules occupy negligible space and have no interactions, may be written as p = RT, (2.2) or p = RT, (2.3) where -3 : density (=m/V) in kg m , 3 -1 : specific volume (=V/m=1/) in m kg . R: specific gas constant (R=R*/M), -1 -1 -1 -1 [R=287 J kg K for dry air (Rd), 461 J kg K for water vapor for water vapor (Rv)].
    [Show full text]
  • [5] Magnetic Densimetry: Partial Specific Volume and Other Applications
    74 MOLECULAR WEIGHT DETERMINATIONS [5] [5] Magnetic Densimetry: Partial Specific Volume and Other Applications By D. W. KUPKE and J. W. BEAMS This chapter consists of three parts. Part I is a summary of the principles and current development of the magnetic densimeter, with which density values may be obtained conveniently on small volumes of solution with the speed and accuracy required for present-day ap- plications in protein chemistry. In Part II, the applications, including definitions, are outlined whereby the density property may be utilized for the study of protein solutions. Finally, in Part III, some practical aspects on the routine determination of densities of protein solutions by magnetic densimetry are listed. Part I. Magnetic Densimeter The magnetic densimeter measures by electromagnetic methods the vertical (up or down) force on a totally immersed buoy. From these measured forces together with the known mass and volume of the buoy, the density of the solution can be obtained by employing Archimedes' principle. In practice, it is convenient to eliminate evaluation of the mass and volume of the buoy and to determine the relation of the mag- netic to the mechanical forces on the buoy by direct calibration of the latter when it is immersed in liquids of known density. Several workers have devised magnetic float methods for determin- ing densities, but the method first described by Lamb and Lee I and later improved by MacInnes, Dayhoff, and Ray: is perhaps the most accurate means (~1 part in 106) devised up to that time for determining the densities of solutions. The magnetic method was not widely used, first because it was tedious and required considerable manipulative skill; second, the buoy or float was never stationary for periods long enough to allow ruling out of wall effects, viscosity perturbations, etc.; third, the technique required comparatively large volumes of the solution (350 ml) for accurate measurements.
    [Show full text]
  • Chapter 3 3.4-2 the Compressibility Factor Equation of State
    Chapter 3 3.4-2 The Compressibility Factor Equation of State The dimensionless compressibility factor, Z, for a gaseous species is defined as the ratio pv Z = (3.4-1) RT If the gas behaves ideally Z = 1. The extent to which Z differs from 1 is a measure of the extent to which the gas is behaving nonideally. The compressibility can be determined from experimental data where Z is plotted versus a dimensionless reduced pressure pR and reduced temperature TR, defined as pR = p/pc and TR = T/Tc In these expressions, pc and Tc denote the critical pressure and temperature, respectively. A generalized compressibility chart of the form Z = f(pR, TR) is shown in Figure 3.4-1 for 10 different gases. The solid lines represent the best curves fitted to the data. Figure 3.4-1 Generalized compressibility chart for various gases10. It can be seen from Figure 3.4-1 that the value of Z tends to unity for all temperatures as pressure approach zero and Z also approaches unity for all pressure at very high temperature. If the p, v, and T data are available in table format or computer software then you should not use the generalized compressibility chart to evaluate p, v, and T since using Z is just another approximation to the real data. 10 Moran, M. J. and Shapiro H. N., Fundamentals of Engineering Thermodynamics, Wiley, 2008, pg. 112 3-19 Example 3.4-2 ---------------------------------------------------------------------------------- A closed, rigid tank filled with water vapor, initially at 20 MPa, 520oC, is cooled until its temperature reaches 400oC.
    [Show full text]
  • Ideal Gasses Is Known As the Ideal Gas Law
    ESCI 341 – Atmospheric Thermodynamics Lesson 4 –Ideal Gases References: An Introduction to Atmospheric Thermodynamics, Tsonis Introduction to Theoretical Meteorology, Hess Physical Chemistry (4th edition), Levine Thermodynamics and an Introduction to Thermostatistics, Callen IDEAL GASES An ideal gas is a gas with the following properties: There are no intermolecular forces, except during collisions. All collisions are elastic. The individual gas molecules have no volume (they behave like point masses). The equation of state for ideal gasses is known as the ideal gas law. The ideal gas law was discovered empirically, but can also be derived theoretically. The form we are most familiar with, pV nRT . Ideal Gas Law (1) R has a value of 8.3145 J-mol1-K1, and n is the number of moles (not molecules). A true ideal gas would be monatomic, meaning each molecule is comprised of a single atom. Real gasses in the atmosphere, such as O2 and N2, are diatomic, and some gasses such as CO2 and O3 are triatomic. Real atmospheric gasses have rotational and vibrational kinetic energy, in addition to translational kinetic energy. Even though the gasses that make up the atmosphere aren’t monatomic, they still closely obey the ideal gas law at the pressures and temperatures encountered in the atmosphere, so we can still use the ideal gas law. FORM OF IDEAL GAS LAW MOST USED BY METEOROLOGISTS In meteorology we use a modified form of the ideal gas law. We first divide (1) by volume to get n p RT . V we then multiply the RHS top and bottom by the molecular weight of the gas, M, to get Mn R p T .
    [Show full text]
  • Pressure Vs. Volume and Boyle's
    Pressure vs. Volume and Boyle’s Law SCIENTIFIC Boyle’s Law Introduction In 1642 Evangelista Torricelli, who had worked as an assistant to Galileo, conducted a famous experiment demonstrating that the weight of air would support a column of mercury about 30 inches high in an inverted tube. Torricelli’s experiment provided the first measurement of the invisible pressure of air. Robert Boyle, a “skeptical chemist” working in England, was inspired by Torricelli’s experiment to measure the pressure of air when it was compressed or expanded. The results of Boyle’s experiments were published in 1662 and became essentially the first gas law—a mathematical equation describing the relationship between the volume and pressure of air. What is Boyle’s law and how can it be demonstrated? Concepts • Gas properties • Pressure • Boyle’s law • Kinetic-molecular theory Background Open end Robert Boyle built a simple apparatus to measure the relationship between the pressure and volume of air. The apparatus ∆h ∆h = 29.9 in. Hg consisted of a J-shaped glass tube that was Sealed end 1 sealed at one end and open to the atmosphere V2 = /2V1 Trapped air (V1) at the other end. A sample of air was trapped in the sealed end by pouring mercury into Mercury the tube (see Figure 1). In the beginning of (Hg) the experiment, the height of the mercury Figure 1. Figure 2. column was equal in the two sides of the tube. The pressure of the air trapped in the sealed end was equal to that of the surrounding air and equivalent to 29.9 inches (760 mm) of mercury.
    [Show full text]
  • TABLE A-2 Properties of Saturated Water (Liquid–Vapor): Temperature Table Specific Volume Internal Energy Enthalpy Entropy # M3/Kg Kj/Kg Kj/Kg Kj/Kg K Sat
    720 Tables in SI Units TABLE A-2 Properties of Saturated Water (Liquid–Vapor): Temperature Table Specific Volume Internal Energy Enthalpy Entropy # m3/kg kJ/kg kJ/kg kJ/kg K Sat. Sat. Sat. Sat. Sat. Sat. Sat. Sat. Temp. Press. Liquid Vapor Liquid Vapor Liquid Evap. Vapor Liquid Vapor Temp. Њ v ϫ 3 v Њ C bar f 10 g uf ug hf hfg hg sf sg C O 2 .01 0.00611 1.0002 206.136 0.00 2375.3 0.01 2501.3 2501.4 0.0000 9.1562 .01 H 4 0.00813 1.0001 157.232 16.77 2380.9 16.78 2491.9 2508.7 0.0610 9.0514 4 5 0.00872 1.0001 147.120 20.97 2382.3 20.98 2489.6 2510.6 0.0761 9.0257 5 6 0.00935 1.0001 137.734 25.19 2383.6 25.20 2487.2 2512.4 0.0912 9.0003 6 8 0.01072 1.0002 120.917 33.59 2386.4 33.60 2482.5 2516.1 0.1212 8.9501 8 10 0.01228 1.0004 106.379 42.00 2389.2 42.01 2477.7 2519.8 0.1510 8.9008 10 11 0.01312 1.0004 99.857 46.20 2390.5 46.20 2475.4 2521.6 0.1658 8.8765 11 12 0.01402 1.0005 93.784 50.41 2391.9 50.41 2473.0 2523.4 0.1806 8.8524 12 13 0.01497 1.0007 88.124 54.60 2393.3 54.60 2470.7 2525.3 0.1953 8.8285 13 14 0.01598 1.0008 82.848 58.79 2394.7 58.80 2468.3 2527.1 0.2099 8.8048 14 15 0.01705 1.0009 77.926 62.99 2396.1 62.99 2465.9 2528.9 0.2245 8.7814 15 16 0.01818 1.0011 73.333 67.18 2397.4 67.19 2463.6 2530.8 0.2390 8.7582 16 17 0.01938 1.0012 69.044 71.38 2398.8 71.38 2461.2 2532.6 0.2535 8.7351 17 18 0.02064 1.0014 65.038 75.57 2400.2 75.58 2458.8 2534.4 0.2679 8.7123 18 19 0.02198 1.0016 61.293 79.76 2401.6 79.77 2456.5 2536.2 0.2823 8.6897 19 20 0.02339 1.0018 57.791 83.95 2402.9 83.96 2454.1 2538.1 0.2966 8.6672 20 21 0.02487 1.0020
    [Show full text]
  • The Application of Temperature And/Or Pressure Correction Factors in Gas Measurement COMBINED BOYLE’S – CHARLES’ GAS LAWS
    The Application of Temperature and/or Pressure Correction Factors in Gas Measurement COMBINED BOYLE’S – CHARLES’ GAS LAWS To convert measured volume at metered pressure and temperature to selling volume at agreed base P1 V1 P2 V2 pressure and temperature = T1 T2 Temperatures & Pressures vary at Meter Readings must be converted to Standard conditions for billing Application of Correction Factors for Pressure and/or Temperature Introduction: Most gas meters measure the volume of gas at existing line conditions of pressure and temperature. This volume is usually referred to as displaced volume or actual volume (VA). The value of the gas (i.e., heat content) is referred to in gas measurement as the standard volume (VS) or volume at standard conditions of pressure and temperature. Since gases are compressible fluids, a meter that is measuring gas at two (2) atmospheres will have twice the capacity that it would have if the gas is being measured at one (1) atmosphere. (Note: One atmosphere is the pressure exerted by the air around us. This value is normally 14.696 psi absolute pressure at sea level, or 29.92 inches of mercury.) This fact is referred to as Boyle’s Law which states, “Under constant tempera- ture conditions, the volume of gas is inversely proportional to the ratio of the change in absolute pressures”. This can be expressed mathematically as: * P1 V1 = P2 V2 or P1 = V2 P2 V1 Charles’ Law states that, “Under constant pressure conditions, the volume of gas is directly proportional to the ratio of the change in absolute temperature”. Or mathematically, * V1 = V2 or V1 T2 = V2 T1 T1 T2 Gas meters are normally rated in terms of displaced cubic feet per hour.
    [Show full text]
  • Lecture 6: Entropy
    Matthew Schwartz Statistical Mechanics, Spring 2019 Lecture 6: Entropy 1 Introduction In this lecture, we discuss many ways to think about entropy. The most important and most famous property of entropy is that it never decreases Stot > 0 (1) Here, Stot means the change in entropy of a system plus the change in entropy of the surroundings. This is the second law of thermodynamics that we met in the previous lecture. There's a great quote from Sir Arthur Eddington from 1927 summarizing the importance of the second law: If someone points out to you that your pet theory of the universe is in disagreement with Maxwell's equationsthen so much the worse for Maxwell's equations. If it is found to be contradicted by observationwell these experimentalists do bungle things sometimes. But if your theory is found to be against the second law of ther- modynamics I can give you no hope; there is nothing for it but to collapse in deepest humiliation. Another possibly relevant quote, from the introduction to the statistical mechanics book by David Goodstein: Ludwig Boltzmann who spent much of his life studying statistical mechanics, died in 1906, by his own hand. Paul Ehrenfest, carrying on the work, died similarly in 1933. Now it is our turn to study statistical mechanics. There are many ways to dene entropy. All of them are equivalent, although it can be hard to see. In this lecture we will compare and contrast dierent denitions, building up intuition for how to think about entropy in dierent contexts. The original denition of entropy, due to Clausius, was thermodynamic.
    [Show full text]
  • Derivation of Pressure Loss to Leak Rate Formula from the Ideal Gas Law
    Derivation of Pressure loss to Leak Rate Formula from the Ideal Gas Law APPLICATION BULLETIN #143 July, 2004 Ideal Gas Law PV = nRT P (pressure) V (volume) n (number of moles of gas) T (temperature) R(constant) After t seconds, if the leak rate is L.R (volume of gas that escapes per second), the moles of gas lost from the test volume will be: L.R. (t) Patm Nlost = -------------------- RT And the moles remaining in the volume will be: PV L.R. (t) Patm n’ = n – Nl = ----- - ------------------- RT RT Assuming a constant temperature, the pressure after time (t) is: PV L.R. (t) Patm ------ - --------------- RT n’ RT RT RT L.R. (t) Patm P’ = ------------ = ------------------------- = P - ------------------ V V V L.R. (t) Patm dPLeak = P - P’ = ------------------ V Solving for L.R. yields: V dPLeak L.R. = -------------- t Patm The test volume, temperature, and Patm are considered constants under test conditions. The leak rate is calculated for the volume of gas (measured under standard atmospheric conditions) per time that escapes from the part. Standard atmospheric conditions (i.e. 14.696 psi, 20 C) are defined within the Non- Destructive Testing Handbook, Second Edition, Volume One Leak Testing, by the American Society of Nondestructive Testing. Member of TASI - A Total Automated Solutions Inc. Company 5555 Dry Fork Road Cleves, OH 45002 Tel (513) 367-6699 Fax (513) 367-5426 Website: http://www.cincinnati-test.com Email: [email protected] Because most testing is performed without adequate fill and stabilization time to allow for all the dynamic, exponential effects of temperature, volume change, and virtual leaks produced by the testing process to completely stop, there will be a small and fairly consistent pressure loss associated with a non- leaking master part.
    [Show full text]
  • Chapter 2 Approximate Thermodynamics
    Chapter 2 Approximate Thermodynamics 2.1 Atmosphere Various texts (Byers 1965, Wallace and Hobbs 2006) provide elementary treatments of at- mospheric thermodynamics, while Iribarne and Godson (1981) and Emanuel (1994) present more advanced treatments. We provide only an approximate treatment which is accept- able for idealized calculations, but must be replaced by a more accurate representation if quantitative comparisons with the real world are desired. 2.1.1 Dry entropy In an atmosphere without moisture the ideal gas law for dry air is p = R T (2.1) ρ d where p is the pressure, ρ is the air density, T is the absolute temperature, and Rd = R/md, R being the universal gas constant and md the molecular weight of dry air. If moisture is present there are minor modications to this equation, which we ignore here. The dry entropy per unit mass of air is sd = Cp ln(T/TR) − Rd ln(p/pR) (2.2) where Cp is the mass (not molar) specic heat of dry air at constant pressure, TR is a constant reference temperature (say 300 K), and pR is a constant reference pressure (say 1000 hPa). Recall that the specic heats at constant pressure and volume (Cv) are related to the gas constant by Cp − Cv = Rd. (2.3) A variable related to the dry entropy is the potential temperature θ, which is dened Rd/Cp θ = TR exp(sd/Cp) = T (pR/p) . (2.4) The potential temperature is the temperature air would have if it were compressed or ex- panded (without condensation of water) in a reversible adiabatic fashion to the reference pressure pR.
    [Show full text]