Modelling Congestion in Passenger Transit Networks Ektoras Chandakas
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Doc Problèmatique
Contenus Articles Transport 1 Grand Paris Express 1 Société du Grand Paris 16 Syndicat des transports d'Île-de-France 22 Arc Express 31 Réseau de transport public du Grand Paris 41 Urbanisme 54 Politique de la ville 54 Agence nationale pour la rénovation urbaine 59 Établissement public d'aménagement 63 Opération d'intérêt national 64 Établissement public foncier 65 Schéma directeur de la région Île-de-France 69 EPCI 74 Communauté d'agglomération 74 Liste des intercommunalités du Val-de-Marne 78 Communauté d'agglomération Plaine centrale du Val-de-Marne 81 Communauté d'agglomération Seine Amont 84 Références Sources et contributeurs de l’article 87 Source des images, licences et contributeurs 88 Licence des articles Licence 90 1 Transport Grand Paris Express Cet article ou cette section contient des informations sur un projet de transport en Île-de-France. Il se peut que ces informations soient de nature spéculative et que leur teneur change considérablement alors que les événements approchent. Grand Paris Express Situation Île-de-France Type Métro automatique [1] Entrée en service entre 2020 et 2030, Longueur du réseau 200 km Lignes 4 Gares 72 Lignes du réseau Réseaux connexes TC en Île-de-France : Métro de Paris RER d'Île-de-France Transilien Tramway d'Île-de-France Autobus d'Île-de-France [2] modifier Le Grand Paris Express est un projet de réseau composé de quatre lignes de métro automatique autour de Paris, et de l'extension de deux lignes existantes. D'une longueur totale de 200 kilomètres[], il doit être réalisé par la Société du Grand Paris (SGP) dans le cadre d'un accord avec le Syndicat des transports d'Île-de-France (STIF). -

Szám Rendsz Teljes Név Épül Beszer Selejt Selejt Más
Szám Rendsz Teljes név Épül Beszer Selejt Selejt Más 08 1808 VP 06 Renault PR180 1986 1992 ? PR 180.2 10 1810 VP 06 Renault PR180 1986 1992 ? PR 180.2 11 1811 VP 06 Renault PR180 1986 1992 ? PR 180.2 13 1813 VP 06 Renault PR180 1986 1992 ? PR 180.2 15 1810 VP 06 Renault PR180 1986 1992 2005 2005 PR 180.2 12 1812 VP 06 Renault PR180 1986 1992 2005 2005 PR 180.2 14 5914 VP 06 Renault PR180 1986 1992 ? PR 180.2 19 219 VQ 06 Renault PR100 1986 1992 ? PR 100.2 18 218 VQ 06 Renault PR100 1986 1992 ? PR 100.2 16 216 VQ 06 Renault PR100 1986 1992 ? PR 100.2 09 1809 VP 06 Renault PR180 1986 1992 2006 PR 180.2 17 217 VQ 06 Renault PR100 1986 1992 2000 PR 100.2 28 828 VY 06 Renault PR180 1987 1992 ? PR 180.2 27 827 VY 06 Renault PR180 1987 1992 ? PR 180.2 29 829 VY 06 Renault PR180 1987 1992 ? PR 180.2 33 833 VY 06 Renault PR180 1987 1992 ? PR 180.2 30 830 VY 06 Renault PR180 1987 1992 ? PR 180.2 31 831 VY 06 Renault PR180 1987 1992 ? PR 180.2 32 832 VY 06 Renault PR180 1987 1992 ? PR 180.2 58 4758 WN 06 Renault R312 1988 1992 ? 57 1257 WN 06 Renault R312 1988 1992 ? 51 6251 WL 06 Renault PR180 1988 1992 ? PR 180.2 50 6250 WL 06 Renault PR180 1988 1992 ? PR 180.2 52 6252 WL 06 Renault PR180 1988 1992 ? PR180.2 53 6253 WL 06 Renault PR180 1988 1992 ? PR180.2 54 6254 WL 06 Renault PR180 1988 1992 ? PR180.2 55 155 WN 06 Renault R312 1988 1992 ? 64 164 WN 06 Renault R312 1988 1992 ? 63 163 WN 06 Renault R312 1988 1992 ? 62 4762 WN 06 Renault R312 1988 1992 ? 61 4761 WN 06 Renault R312 1988 1992 ? 60 4760 WN 06 Renault R312 1988 1992 ? 59 1259 WN 06 -

© Norwich Bus Page 2013 Norfolk Green Fleet List – 1 St December
© Norwich Bus Page 2013 Norfolk Green fleet List – 1st December 2013 Fleet No. Registration Chassis/Body Livery Name 1 YE52FHF DAF DB250LF Optare Spectra Norfolk Green Jamie Armstrong 2 YE52FHG DAF DB250LF Optare Spectra New Norfolk Green Reis L Leming 3 YG02FWE DAF DB250LF Optare Spectra Norfolk Green John Palmer 4 YG02FWB DAF DB250LF Optare Spectra Norfolk Green Horace The Tiger 5 YJ03UMK DAF DB250LF Optare Spectra Norfolk Green Frances Burney 6 YJ03UML DAF DB250LF Optare Spectra Norfolk Green Somerset Arthur Maxwell 7 YJ51ZVF DAF DB250LF Optare Spectra Norfolk Green George Vancouver 8 YJ51ZVG DAF DB250LF Optare Spectra New Norfolk Green Ted Martin 9 YG02FWD DAF DB250LF Optare Spectra New Norfolk Green Black Shuck 10 LV52HHP Alexander Dennis Trident ALX400 Norfolk Green John Colton 11 LV52HHR Alexander Dennis Trident ALX400 Norfolk Green Samuel Pepys 13 PX55AHF Dennis Trident East Lancs Myllenium Lolyne New Norfolk Green William D'Albini 14 PX55AHJ Dennis Trident East Lancs Myllenium Lolyne New Norfolk Green Jessie & George Ruhms 21 SN12EHM Alexander Dennis Enviro400 New Norfolk Green Johnny Douglas 22 SN12EHO Alexander Dennis Enviro400 New Norfolk Green William Henry Mann 23 SN13EEA Alexander Dennis Enviro400 New Norfolk Green -- 24 SN13EEB Alexander Dennis Enviro400 New Norfolk Green -- 101 YJ56WUG Optare X1200 Tempo New Norfolk Green Sir Peter Scott 102 YJ56WUH Optare X1200 Tempo Norfolk Green Frederick Savage 103 YJ57YCC Optare X1200 Tempo Norfolk Green Robert Stephenson 104 YJ57YCD Optare X1200 Tempo Norfolk Green Ruth, Lady Fermoy -

Modèle De Rapport Commercial
RAPPORT D’ÉTUDE 03/12/2009 N° DRC-09-104243-11651A INTER’MODAL Vers une meilleure maîtrise de l’exposition individuelle par inhalation des populations à la pollution atmosphérique lors de leurs déplacements urbains INTER’MODAL Vers une meilleure maîtrise de l’exposition individuelle par inhalation des populations à la pollution atmosphérique lors de leurs déplacements urbains Ministère de l’Ecologie, de l’Energie, du Développement Durable et de la Mer (MEEDDM) Bureau de l'Air & Bureau de la prospective et de l'évaluation des données Grande Arche de la Défense - Paris Nord 92055 PARIS LA DEFENSE CEDEX Liste des personnes ayant participé à l’étude : S.Fable, I.Fraboulet, F.Godefroy, G.Jantolek, J.Queron, B.Triart. DRC-09-104243-11651A - 1 / 117 - PRÉAMBULE Le présent rapport a été établi sur la base des informations fournies à l'INERIS, des données (scientifiques ou techniques) disponibles et objectives et de la réglementation en vigueur. La responsabilité de l'INERIS ne pourra être engagée si les informations qui lui ont été communiquées sont incomplètes ou erronées. Les avis, recommandations, préconisations ou équivalent qui seraient portés par l'INERIS dans le cadre des prestations qui lui sont confiées, peuvent aider à la prise de décision. Etant donné la mission qui incombe à l'INERIS de par son décret de création, l'INERIS n'intervient pas dans la prise de décision proprement dite. La responsabilité de l'INERIS ne peut donc se substituer à celle du décideur. Le destinataire utilisera les résultats inclus dans le présent rapport intégralement ou sinon de manière objective. -

New Signage System for Improving Pedestrian Flow on Single-Exit Metro Stations: Focus on Paris Metro Line 4 Historical Stations Matteo Porrino, Stefano Dal Pont
New Signage System for Improving Pedestrian Flow on Single-Exit Metro Stations: Focus on Paris Metro Line 4 Historical Stations Matteo Porrino, Stefano Dal Pont To cite this version: Matteo Porrino, Stefano Dal Pont. New Signage System for Improving Pedestrian Flow on Single-Exit Metro Stations: Focus on Paris Metro Line 4 Historical Stations. International Journal of Advance Engineering and Research Development, 2018, 14. hal-01945816 HAL Id: hal-01945816 https://hal.archives-ouvertes.fr/hal-01945816 Submitted on 31 Jan 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. International Journal Of Engineering Research And Development e- ISSN: 2278-067X, p-ISSN: 2278-800X, www.ijerd.com Volume 14, Issue 7 (July Ver. I 2018), PP.06-17 New Signage System For Improving Pedestrian Flow On Single- Exit Metro Stations:Focus On Paris Metro Line 4 Historical Stations Matteo Porrino, Meng, Phd, Stefano Dal Pont, Prof., Phd, Associate Professor, ENSA Paris-Malaquais, Université Paris-Est, Paris Professor, Université Grenoble-Alpes, Grenoble Corresponding Author- Stefano Dal Pont, Prof., Phd ABSTRACT; For a number of years now, the use of the Metro is steadily augmenting, making it more and more difficult to ensure traffic regularity (due to a variety of technical problems, increases in exiting/boarding time and passenger accidents), which determines a loss in the system‟s energy efficiency and the increase of traction current expenses. -

Squaring the Circle: the Bhls Concept
SQUARING THE CIRCLE: THE BHLS CONCEPT María Eugenia López Lambas Associated Professor of Transport ETSI Caminos, Canales y Puertos –Universidad Politécnica de Madrid (UPM), Spain Cristina Valdés PhD Researcher Transyt-UPM, Spain ABSTRACT The transport system known as Bus Rapid Transit (BRT) was launched in Curitiba, Brazil, in 1974 as a means of offering efficient and effective bus travel within the fast expanding city. This experience, together with other such Ottawa (since 1983) or Quito (since 1994), has proven to be an efficient and effective solution to mass transport. Throughout Europe similar experiences have started to be developed, but addressing a different concept in terms of quality of service. Indeed, bus systems such as the “trunk network”, in Sweden, the Metrobus, in Germany, or the BHNS (Bus à Haut Niveau de Service in France), approach the quality of service from a wider perspective than the BRT, as it considers aspects such as image and comfort, apart from speed, frequency or reliability. These new systems - BHLS (Buses with a High Quality of Service) - allow to combine quality of service of tramways with the lower costs and higher flexibility of bus systems, offering very interesting solutions in terms of accessibility, as well as a wide range of service levels, that allows the system to be adapted to the different urban contexts (size, population, density , etc) The economic situation we are facing has beard a lack of funds that, at the end, means an opportunity for BHLS, called to play an important role in public transport: less costs with the same quality of service seems to be a very attractive option. -
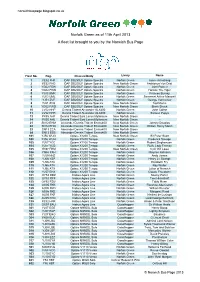
Norfolk Green Fleet List UPDATED
norwichbuspage.blogspot.co.uk Norfolk Green as of 11th April 2013 A fleet list brought to you by the Norwich Bus Page Fleet No. Reg. Chassis/Body Livery Name 1 YE52 FHF DAF DB250LF Optare Spectra Norfolk Green Jamie Armstrong 2 YE52 FHG DAF DB250LF Optare Spectra New Norfolk Green Andrianus Van Driel 3 YG02 FEW DAF DB250LF Optare Spectra Norfolk Green John Palmer 4 YG02 FWB DAF DB250LF Optare Spectra Norfolk Green Horace The Tiger 5 YJ03 UMK DAF DB250LF Optare Spectra Norfolk Green Frances Burney 6 YJ03 UML DAF DB250LF Optare Spectra Norfolk Green Somerset Arthur Maxwell 7 YJ51 ZVF DAF DB250LF Optare Spectra Norfolk Green George Vancouver 8 YJ51 ZVG DAF DB250LF Optare Spectra New Norfolk Green Ted Martin 9 YG02 FWD DAF DB250LF Optare Spectra New Norfolk Green Black Shuck 10 LV52 HHP Dennis Trident Alexander ALX400 Norfolk Green John Colton 11 LV52 HHR Dennis Trident Alexander ALX400 Norfolk Green Samuel Pepys 13 PX55 AHF Dennis Trident East Lancs Myllenium New Norfolk Green -- 14 PX55 AHJ Dennis Trident East Lancs Myllenium New Norfolk Green -- 21 SN12 EHM Alexander Dennis Trident Enviro400 New Norfolk Green Johnny Douglas 22 SN12 EHO Alexander Dennis Trident Enviro400 New Norfolk Green William Henry Mann 23 SN13 EEA Alexander Dennis Trident Enviro400 New Norfolk Green -- 24 SN13 EEB Alexander Dennis Trident Enviro400 New Norfolk Green -- 101 YJ56 WUG Optare X1200 Tempo New Norfolk Green Sir Peter Scott 102 YJ56 WUH Optare X1200 Tempo Norfolk Green Frederick Savage 103 YJ57 YCC Optare X1200 Tempo Norfolk Green Robert Stephenson 104 YJ57 -

POUR Un TROLLEYBUS MODERNE Dans L'agglomération Grenobloise
POUR un TROLLEYBUS MODERNE dans l’agglomération grenobloise « Le trolleybus, un moyen de transport durable et performant, quand on le crédite du coût des nuisances évitées » ADTC – janvier 2005 Sommaire Les avantages du trolleybus par rapport à l’autobus : 1. Le trolleybus, un moyen de transport performant 2. Le trolleybus est un moyen de transport non polluant 3. Le trolleybus, un moyen de transport rentable Quelques réponses que l’on peut apporter aux personnes qui se posent la question de la pertinence du retour du trolleybus dans notre agglomération. 1. Le coût du trolleybus 2. L'image du trolleybus 3. La pollution visuelle 4. Existe-t-il des constructeurs européens ? 5. Les installations grenobloises existantes sont-elles réutilisables ? 6. Quelles lignes de bus transformer en lignes de trolleybus à Grenoble ? Pour un trolleybus moderne Page 1 sur 11 dans l’agglomération grenobloise janvier 2005 Les avantages du trolleybus par rapport à l’autobus : 1. Le trolleybus, un moyen de transport performant Grâce à ses caractéristiques, le trolleybus s’inscrit totalement dans le concept de Bus à Haut Niveau de Service (BHNS) Accélération : le trolleybus est plus rapide en accélération, grâce à un couple de démarrage constant (pas d’embrayage, ni de renvoi d’angle, ni de boîte à vitesses) : en 15 secondes, il parcourt 30 % de distance en plus que le bus diesel, ce qui autorise un parc trolleybus inférieur de 7% à un un parc d’autobus offrant le même service. Pentes : le trolleybus est le véhicule de transports en commun le plus adapté pour gravir les pentes (telles celles de La Tronche, de Meylan et de Saint- Martin le Vinoux). -

Engins Métro MP 59
Engins Métro Les engins moteurs de la RATP que l'on étudiera ici sont les rames voyageurs utilisées sur l'ensemble du réseau. Elles sont constituées de rames circulant sur le réseau rail (MF - Matériel Fer) et des rames à pneus (MP - Matériel Pneu). Pour une explication du réseau rail et pneu, RDV à la partie Circulations des Métros et Réseau RATP... MP 59 Le plus anciennes rames du métro parisien sont les MP 59 (Matériels à Pneu dont la conception date de 1959). Ses 4 fois 140 chevaux ont révolutionné, tout comme son prédécesseur le MP55, le matériel roulant. Il circulait auparavant sur les lignes 1, 4 et 11, et reste actuellement présent sur les lignes 4 et 11. Il disparaîtra en 2012 de la ligne 4, remplacé par le MP89. Ici un MP 59 à Porte des Lilas (ligne 11) MF 67 Les rames MF 67 (matériel fer) équipent la majorité des lignes : 3, 3bis, 5 (en cours de remplacement par le MF 2000), 9, 10, 12. Avec les MP 59 et les MP73, ce sont les rames typiques du métro parisien, de par leur forma caractéristique. Véritable remplaçant du matériel Sprague Thomson, il a redonné sa chance au matériel Fer et aux lignes non équipées de pneus . MF 67 à la station de formation Gare du Nord (ancienne station de terminus de la ligne 5) et à Bobigny Pablo Picasso (actuel terminus ligne 5) MP 73 Les rames MP 73 sont une adaptation du MP 59 pour la ligne 6 (mais avec l'esthétique du MF 67). -

Optimalization MRT System
Danny Tandela Advisor : Prof. Kamal Serrhini 1 ` Paris Metropolitan is the major transport systems that serving millions of commuters everyday in metropolitan areas. ` The networks are a high frequency service established mainly in underground tunnels or on elevated tracks separated from other traffic. 2 ` One of the major problem in the subway system is the operational cost that cause by the energy consumption need to be reduce. ` The reducing of energy consumption also lead to the “green transportation” and stakeholders (major of the city) could use the budget for the transportation to another field like education, rural area development, etc. 3 With the proposed approach : ` To know the performance and the amount of the energy that could be reduced ` To know the performance and the travelling time that could be reduced 4 ` Literature Review ` Collecting Data ` Assumption ` Implementation and Analysis ` Limitation and Perspective 5 validation Research Logical Diagram 6 Station Train I Passenger Station II • Train • Station • User/ Passenger • Railway 7 Exit Gate Train Entrance Gate Automatic Ticket Manual Ticket Machine Operator Passengers 8 validation Research Logical Diagram 9 10 11 Ligne Number of stations Length (km) Average interstation (m) 1 25 16,6 692 2 25 12,3 513 3 25 11,7 488 3 bis 4 1,3 433 4 26 10,6 424 5 22 14,6 695 6 28 13,6 504 7 38 22,4 605 7 bis 8 3,1 443 8 37 22,1 614 9 37 19,6 544 10 23 11,7 532 11 13 6,3 525 12 28 13,9 515 13 32 24,3 776 14 9 9 1129 Wikipedia, 2012 12 Types of Number of mass Power Power Acceleration -

INTER'modal Vers Une Meilleure Maîtrise De L'exposition Individuelle
RAPPORT D’ÉTUDE 03/12/2009 N° DRC-09-104243-11651A INTER’MODAL Vers une meilleure maîtrise de l’exposition individuelle par inhalation des populations à la pollution atmosphérique lors de leurs déplacements urbains INTER’MODAL Vers une meilleure maîtrise de l’exposition individuelle par inhalation des populations à la pollution atmosphérique lors de leurs déplacements urbains Ministère de l’Ecologie, de l’Energie, du Développement Durable et de la Mer (MEEDDM) Bureau de l'Air & Bureau de la prospective et de l'évaluation des données Grande Arche de la Défense - Paris Nord 92055 PARIS LA DEFENSE CEDEX Liste des personnes ayant participé à l’étude : S.Fable, I.Fraboulet, F.Godefroy, G.Jantolek, J.Queron, B.Triart. DRC-09-104243-11651A - 1 / 119 - PRÉAMBULE Le présent rapport a été établi sur la base des informations fournies à l'INERIS, des données (scientifiques ou techniques) disponibles et objectives et de la réglementation en vigueur. La responsabilité de l'INERIS ne pourra être engagée si les informations qui lui ont été communiquées sont incomplètes ou erronées. Les avis, recommandations, préconisations ou équivalent qui seraient portés par l'INERIS dans le cadre des prestations qui lui sont confiées, peuvent aider à la prise de décision. Etant donné la mission qui incombe à l'INERIS de par son décret de création, l'INERIS n'intervient pas dans la prise de décision proprement dite. La responsabilité de l'INERIS ne peut donc se substituer à celle du décideur. Le destinataire utilisera les résultats inclus dans le présent rapport intégralement ou sinon de manière objective. -

CR-2019-036.Pdf
Rapport pour le conseil régional SEPTEMBRE 2019 Présenté par Valérie PÉCRESSE Présidente du conseil régional d’Île-de-France COMMUNICATION SUR LES TRANSPORTS CR 2019-036 CONSEIL RÉGIONAL D’ÎLE-DE-FRANCE 2 RAPPORT N° CR 2019-036 Sommaire EXPOSÉ DES MOTIFS........................................................................................................................3 2019-09-06 14:55:26 CONSEIL RÉGIONAL D’ÎLE-DE-FRANCE 3 RAPPORT N° CR 2019-036 EXPOSÉ DES MOTIFS COMMUNICATION Conformément à ses engagements, l’Exécutif régional propose dans la présente communication de dresser un point d’étape de la mise en œuvre de la « révolution des transports ». Il s’agit du troisième rapport qui est présenté au Conseil régional, la précédente communication ayant eu lieu en septembre 2017. La Révolution des transports initiée en 2016 pour palier le vieillissement du réseau se poursuit et les efforts déployés par Île-de-France Mobilités et la Région pour des transports plus modernes, plus confortables, plus ponctuels, plus de moyens pour la sécurité et rééquilibrés territorialement au profit de la grande couronne trop longtemps délaissée portent leurs fruits. Pour porter la révolution des transports, la Région a adopté un budget 2019 particulièrement ambitieux avec 755 M€ d’autorisation de programme pour les investissements (+37% par rapport à 2015) et 773 M€ d’autorisation d’engagement pour le fonctionnement. Le budget d’investissement d’Île-de-France Mobilités a été porté à 2 012 M€ pour l’année 2019, soit une augmentation de 33% par rapport à l’exécution 2018, traduisant la forte accélération du renouvellement du matériel roulant. Son budget de fonctionnement, de 5 982M€, en évolution de +4,2%, reflète essentiellement la dynamique de l’offre nouvelle (y compris l’offre de nouvelles mobilités) et les dépenses liées au Plan de Modernisation de la Billettique.