DOCSLIB.ORG

Fourier Transform.Pdf

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Fourier Transform.Pdf ECE 307 Fourier Transform Z. Aliyazicioglu Electrical & Computer Engineering Dept. Cal Poly Pomona Fourier Transform The Fourier transform (FT) is the extension of the Fourier series to nonperiodic signals. The Fourier transform of a signal exist if satisfies the following condition. ∞ 2 ∫ xt() dt< ∞ −∞ ∞ The Fourier transform X()ω = ∫ xte ()− jtω dt −∞ The inverse Fourier transform (IFT) of X(ω) is x(t)and given by 1 ∞ x()tXed= ∫ (ω ) jtω ω 2π −∞ 1 Fourier Transform Also, The Fourier transform can be defined in terms of frequency of Hertz as ∞ X()fxtedt= ∫ () − jft2π −∞ and corresponding inverse Fourier transform is ∞ x()tXfedf= ∫ () jft2π −∞ Fourier Transform Example: Determine the Fourier transform of a rectangular pulse shown in the following figure x(t) h a /2 ωωaa − jj − jtω h Xhedtee()ω ==− 22 ∫ − jω t −a /2 ωa -a/2 a/2 sin( ) 2haω ==sin( ) ha 2 ω 2 ωa 2 ωa = hasinc 2π 2 Fourier Transform Example: To find in frequency domain, a /2 22ππfa fa − jj − jft2π h Xf()==∫ he dt e22 − e −a /2 − jf2π h = 1, hfasin(π ) ==sin(πfa ) ha a = 1 ππffa ω = hasinc fa X()ω = 2sinc () 2π >> h=1; >> a=1; >> f=-3.5:0.01:3.5; >> w=2*pi*f; >> x=h*a*sinc(w*a/(2*pi)); >> plot (w,x) >> title ('X(\omega)') >> xlabel('\omega'); >> Fourier Transform h = 1, a = 2 ω2 X()ω = 2sinc 2π >> h=1; >> a=1; >> f=-3.5:0.01:3.5; >> w=2*pi*f; >> x=abs(h*a*sinc(w*a/(2*pi))); >> subplot (2,1,1) >> plot (w,x) >> title ('|X(\omega)|') >> xlabel('\omega') >> xp=phase(h*a*sinc(w*a/(2*pi))); >> subplot (2,1,2) >> plot (w,xp) >> title ('phase X(\omega)') >> xlabel('\omega') 3 Fourier Transform Example Determine the Fourier transform of the Delta function δ(t) ∞ Xtedte()ωδ===∫ ()−−jtωω j0 1 −∞ X(ω) 1 ω Fourier Transform Properties of the Fourier Transform We summarize several important properties of the Fourier Transform as follows. 1. Linearity (Superposition) xt()⇔ X (ω ) If xt11()⇔ X (ω ) and 22 Then, ax11() t+⇔+ ax 2 2 () t aX 1 1 (ω ) aX 2 2 (ω ) Proof: ∞∞∞ axt()+= axte ()−−jtωω dta xte () jt dta + xte () − jt ω dt ∫∫∫[]11 2 2 1 1 2 2 −∞ −∞ −∞ =+aX11()ωω aX 2 2 () 4 Fourier Transform Properties of the Fourier Transform 2. Time Shifting If xt()⇔ X (ω ) − jωt0 Then, xt()−⇔ t0 X ()ω e Proof: Let τ =−tt0 then tt= τ + 0 and dt= dτ ∞∞ jt() xt()−= t e− jtω dt x ()τ e−+ωτ 0 dτ ∫∫0 −∞ −∞ ∞ jt = exed− ω 0 ∫ ()τ − jωτ τ −∞ jt = eX− ω 0 ()ω Fourier Transform Let yt()=− xt ( t0 ) j tjt YXeXee()ωω== ()−−ω 00 () ωjX∠ ()ω ω = Xe()ω jX(())∠−ωω t0 Ye()ωωjY∠ ()ω = Xe () j(())∠−Xtωω0 Therefore, the amplitude spectrum of the time shifted signal is the same as the amplitude spectrum of the original signal, and the phase spectrum of the time-shifted signal is the sum of the phase spectrum of the original signal and a linear phase term. 5 Fourier Transform Example: Determine the Fourier transform of the following time shifted rectangular pulse. x(t) h a ωa − jω Xhae()ω = sinc 2 2π t 0 a >> h=1; >> a=1; >> f=-3.5:0.01:3.5; >> w=2*pi*f; >> x=abs(h*a*sinc(w*a/(2*pi)).*exp(- j*w*1/2)); >> subplot (2,1,1) >> plot (w,x) >> title ('|X(\omega)|') >> xlabel('\omega') >> xp=phase(h*a*sinc(w*a/(2*pi)).*exp(- j*w.*1/2)); >> subplot (2,1,2) >> plot (w,xp) >> xlabel('\omega') >> title ('phaseX(\omega)') Fourier Transform 3. Time Scaling If xt()⇔ X (ω ) then 1 ω xat()⇔ X () aa Proof: Let τ = at then ta= τ / and dt= (1/ a ) dτ If , a>0 then If , a<0 then ∞∞ω − j τ ∞∞ω − jtω 1 − j τ 1 x()at e dt= x ()τ ea dτ xate()− jtω dt= x ()ττ ea d ∫∫ ∫∫a −∞ −∞ a −∞ −∞ ∞ ω 1 ω 11− j τ ω = X() ==∫ xe()ττa d X ( ) aa aaa−∞ 6 Fourier Transform Example. if , xt () ⇔ X ( ω ) then find the Fourier transform of the following signals 1 −ω xt(2)−⇔ X ( ) a. 22 b. xt(/5)⇔ 5 X (5)ω 1 −ω c. xt(5(−− 2)) ⇔ X ( ) e− jω 2 55 Example: Find the Fourier transform of the following signal. ω xt11()=∏ () t ⇔ X (ω ) = sinc a. 2π 11ω ω xt() (5) t X ( ) X ( ) sinc b. 221=∏ ⇔ω = = 555 10π c. ω xt331()=∏ ( t /5) ⇔ X (ωω ) = 5 X (5) = 5sinc 0.4π Fourier Transform 4. Duality (Symmetry) If xt()⇔ X (ω ) then Xt()⇔− 2π x (ω ) or X()txf⇔ (− ) Proof: Since t and ω are arbitrary variables in the inverse Fourier transform 1 ∞ x()tXed= ∫ (ω ) jtω ω 2π −∞ we can replace ω with t and t with - ω to get ∞ 1 − jtω Therefore, xXtedt()−=ω ∫ () 2π −∞ ∞ F{}Xt()==−∫ Xte ()− jtω dt 2π x (ω ) −∞ 7 Fourier Transform Similarly, if we can replace f with t and t with -f in the inverse Fourier transform ∞ x()tXfedf= ∫ () jft2π −∞ to get ∞ x()−=fXtedf∫ ()− jft2π −∞ Therefore, F{Xt()} = x (− f ) Fourier Transform Example: xt()=⇔δ () t X (ω ) = 1 Applying symmetry property, xt()=⇔ 1 X (ω ) = 2πδ ( −= ω ) 2 πδ ( ω ) (δ () ω is even function) or xt()=⇔ 1 Xf () =−=δ ( f )δ () f Example: ta ω xt()=⇔= rect X (ω ) a sinc a 2π ta −ω ω xt()=⇔== a sinc X (ωπ ) 2 rect 2 π rect 2π aa a Let c = then ac= 2π 2π ωω1 x() t=⇔== a sinc() ct X (ωπ ) 2 rect rect 22πcc π c 8 Fourier Transform Time Reversal If xt()⇔ X (ω ) then xt()−⇔− X (ω ) Proof: Let −=t τ . Then t = −τ and dt= − dτ ∞∞ ∫∫xtedt()−=−=−−−−jtωωτ x ()τ e j() dτω X ( ) −∞ −∞ Fourier Transform Frequency Shifting If xt()⇔ X (ω ) then − jtωc xte()⇔− X (ω ωc ) Proof: ∞∞ xte()jtωωωcc e− jtω dt==− xte ()−− j() t dt X (ω ω ) ∫∫ c −∞ −∞ 9 Fourier Transform Example: Determine the Fourier transform of cos ω c t and sinωct 11 xt()==+ cosω t ejtωωcc e− jt ⇔=−++ X (ωπδωωδωω )[] ( ) ( ) ccc22 or 11 1 x()tteeXfffff==+ cosωδδjtωωcc− jt ⇔=−++ ()[] ( ) ( ) ccc22 2 X(f) 1/2 -fc fc f The phase spectrum is zero everywhere. Fourier Transform 11jtωωcc− jt xt()== sinωc t e − e ⇔=−−−+ X (ωπδωωδωω ) j [] (cc ) ( ) 22jj 11 − j x()ttee== sinωδδjtωωcc −− jt ⇔= Xfffff ()[] ( −−+ ) ( ) c 22jj 2cc |X(f)| 1/2 -fc fc f θ(f) π/2 fc -fc f -π/2 10 Fourier Transform 7. Modulation If xt()⇔ X (ω ) then 1 xt( )cos(ωccc t )⇔−++[] X (ωω ) X ( ωω ) 2 Proof: ∞∞ 1 jt jt xt()cos(ω te )−−jtωω dt=+ xt () eωωcc e e jt dt ∫∫c −∞ −∞ 2 ∞∞ 1 −−jt()ωω −+ jt () ωω =+ xte()cc dt xte () dt 2 ∫∫ −∞ −∞ 1 =−++[]XX()()ωωcc ωω 2 Fourier Transform 8. Time Differentiation: If xt()⇔ X (ω ) then General case n dx() t dxt() n ⇔ jXω ()ω n ⇔ ()()jXω ω dt dt Proof: Taking the derivative of the inverse Fourier transform 1 ∞ x()tXed= ∫ (ω ) jtω ω 2π −∞ we obtain dx() t 1 ∞ = ∫ jωXed()ωωjtω dt 2π −∞ Therefore dx() t ⇔ jXω ()ω dt 11 Fourier Transform 9. Time Differentiation: If xt()⇔ X (ω ) then General case dXn ()ω dX() jω txtnn()⇔ j tx() t⇔ j dω n dω Proof: Taking derivative of Fourier Transform ∞ − jtω X()ω = ∫ xte () dt with respect to ω, we obtain −∞ dX()ω ∞ =−∫ ()()jtxte− jtω dt dω −∞ dX() jω Therefore tx() t⇔ j dω Fourier Transform 10 Conjugate If xt()⇔ X (ω ) then xt**()⇔− X (ω ) Proof: * ∞∞ *()*−−−jtωω j t ∫∫xte() dt= xte () dt=− X (ω ) −∞ −∞ If x(t) is real x * () txt = () so that XX()ω = * (−ω ) 12 Fourier Transform 11. Convolution If xt()⇔ X (ω ), ht () ⇔ H ( ω ) , and yt () ⇔ Y (ω ) ∞ yt()==− ht ()* xt ()∫ h (τ ) xt (ττ ) d −∞ YHX()ω = ()()ωω Proof: ∞∞ − jtω Yhxtdedt()ωτττ=−∫∫ ()( ) −∞ −∞ Interchanging the order of integration, we obtain ∞∞ ∞∞ −−jjωτ ωτ Yhxtedtd()ω =− ()τττ ( )− jtω YhXedXhed()ω ==∫∫ ()()τω τ () ω () τ τ ∫∫−∞ −∞ −∞ −∞ = XH()()ωω Fourier Transform 12. Multiplication xt()⇔ X (ω ) If 11, and xt 22 () ⇔ X (ω ) 11∞ x ()tx () t⇔=− X (ωω )* X ( ) X ( vX ) ( ω vdv ) 12 1 2∫ 1 2 22ππ−∞ or ∞ x ()tx () t⇔=− X ()* f X () f X ( vX ) ( f vdv ) 12 1 2∫ 1 2 −∞ 13 Fourier Transform 13. Parseval’s Theorem If xt11()⇔ X (ω ), then total normalized(based on one ohms resistor) energy E of and x(t) is given by ∞∞∞ 2221 ExtdtXd==∫∫∫() (ωω ) = Xfdf () −∞2π −∞ −∞ Proof ∞∞ ∞∞ 2 ** 1 − jtω x()tdtxtxtdtxtXeddt== () () () (ωω ) ∫∫ ∫∫2 −∞ −∞ −∞ π −∞ Interchanging the order of integration, we obtain Fourier Transform Proof (cont) ∞∞∞ 2 1 * − jtω x()tdt= X (ω ) xtedtd () ω ∫∫∫2 −∞π −∞ −∞ 1 ∞ = ∫ XXd* ()()ωωω 2π −∞ ∞ 1 2 = ∫ Xd()ωω 2π −∞ 14.
Load more

Recommended publications
  • FOURIER TRANSFORM Very Broadly Speaking, the Fourier Transform Is a Systematic Way to Decompose “Generic” Functions Into
    FOURIER TRANSFORM TERENCE TAO Very broadly speaking, the Fourier transform is a systematic way to decompose “generic” functions into a superposition of “symmetric” functions. These symmetric functions are usually quite explicit (such as a trigonometric function sin(nx) or cos(nx)), and are often associated with physical concepts such as frequency or energy. What “symmetric” means here will be left vague, but it will usually be associated with some sort of group G, which is usually (though not always) abelian. Indeed, the Fourier transform is a fundamental tool in the study of groups (and more precisely in the representation theory of groups, which roughly speaking describes how a group can define a notion of symmetry). The Fourier transform is also related to topics in linear algebra, such as the representation of a vector as linear combinations of an orthonormal basis, or as linear combinations of eigenvectors of a matrix (or a linear operator). To give a very simple prototype of the Fourier transform, consider a real-valued function f : R → R. Recall that such a function f(x) is even if f(−x) = f(x) for all x ∈ R, and is odd if f(−x) = −f(x) for all x ∈ R. A typical function f, such as f(x) = x3 + 3x2 + 3x + 1, will be neither even nor odd. However, one can always write f as the superposition f = fe + fo of an even function fe and an odd function fo by the formulae f(x) + f(−x) f(x) − f(−x) f (x) := ; f (x) := . e 2 o 2 3 2 2 3 For instance, if f(x) = x + 3x + 3x + 1, then fe(x) = 3x + 1 and fo(x) = x + 3x.
    [Show full text]
  • Finding Pi Project
    Name: ________________________ Finding Pi - Activity Objective: You may already know that pi (π) is a number that is approximately equal to 3.14. But do you know where the number comes from? Let's measure some round objects and find out. Materials: • 6 circular objects Some examples include a bicycle wheel, kiddie pool, trash can lid, DVD, steering wheel, or clock face. Be sure each object you choose is shaped like a perfect circle. • metric tape measure Be sure your tape measure has centimeters on it. • calculator It will save you some time because dividing with decimals can be tricky. • “Finding Pi - Table” worksheet It may be attached to this page, or on the back. What to do: Step 1: Choose one of your circular objects. Write the name of the object on the “Finding Pi” table. Step 2: With the centimeter side of your tape measure, accurately measure the distance around the outside of the circle (the circumference). Record your measurement on the table. Step 3: Next, measure the distance across the middle of the object (the diameter). Record your measurement on the table. Step 4: Use your calculator to divide the circumference by the diameter. Write the answer on the table. If you measured carefully, the answer should be about 3.14, or π. Repeat steps 1 through 4 for each object. Super Teacher Worksheets - www.superteacherworksheets.com Name: ________________________ “Finding Pi” Table Measure circular objects and complete the table below. If your measurements are accurate, you should be able to calculate the number pi (3.14). Is your answer name of circumference diameter circumference ÷ approximately circular object measurement (cm) measurement (cm) diameter equal to π? 1.
    [Show full text]
  • An Introduction to Fourier Analysis Fourier Series, Partial Differential Equations and Fourier Transforms
    An Introduction to Fourier Analysis Fourier Series, Partial Differential Equations and Fourier Transforms Notes prepared for MA3139 Arthur L. Schoenstadt Department of Applied Mathematics Naval Postgraduate School Code MA/Zh Monterey, California 93943 August 18, 2005 c 1992 - Professor Arthur L. Schoenstadt 1 Contents 1 Infinite Sequences, Infinite Series and Improper Integrals 1 1.1Introduction.................................... 1 1.2FunctionsandSequences............................. 2 1.3Limits....................................... 5 1.4TheOrderNotation................................ 8 1.5 Infinite Series . ................................ 11 1.6ConvergenceTests................................ 13 1.7ErrorEstimates.................................. 15 1.8SequencesofFunctions.............................. 18 2 Fourier Series 25 2.1Introduction.................................... 25 2.2DerivationoftheFourierSeriesCoefficients.................. 26 2.3OddandEvenFunctions............................. 35 2.4ConvergencePropertiesofFourierSeries.................... 40 2.5InterpretationoftheFourierCoefficients.................... 48 2.6TheComplexFormoftheFourierSeries.................... 53 2.7FourierSeriesandOrdinaryDifferentialEquations............... 56 2.8FourierSeriesandDigitalDataTransmission.................. 60 3 The One-Dimensional Wave Equation 70 3.1Introduction.................................... 70 3.2TheOne-DimensionalWaveEquation...................... 70 3.3 Boundary Conditions ............................... 76 3.4InitialConditions................................
    [Show full text]
  • Evaluating Fourier Transforms with MATLAB
    ECE 460 – Introduction to Communication Systems MATLAB Tutorial #2 Evaluating Fourier Transforms with MATLAB In class we study the analytic approach for determining the Fourier transform of a continuous time signal. In this tutorial numerical methods are used for finding the Fourier transform of continuous time signals with MATLAB are presented. Using MATLAB to Plot the Fourier Transform of a Time Function The aperiodic pulse shown below: x(t) 1 t -2 2 has a Fourier transform: X ( jf ) = 4sinc(4π f ) This can be found using the Table of Fourier Transforms. We can use MATLAB to plot this transform. MATLAB has a built-in sinc function. However, the definition of the MATLAB sinc function is slightly different than the one used in class and on the Fourier transform table. In MATLAB: sin(π x) sinc(x) = π x Thus, in MATLAB we write the transform, X, using sinc(4f), since the π factor is built in to the function. The following MATLAB commands will plot this Fourier Transform: >> f=-5:.01:5; >> X=4*sinc(4*f); >> plot(f,X) In this case, the Fourier transform is a purely real function. Thus, we can plot it as shown above. In general, Fourier transforms are complex functions and we need to plot the amplitude and phase spectrum separately. This can be done using the following commands: >> plot(f,abs(X)) >> plot(f,angle(X)) Note that the angle is either zero or π. This reflects the positive and negative values of the transform function. Performing the Fourier Integral Numerically For the pulse presented above, the Fourier transform can be found easily using the table.
    [Show full text]
  • Fourier Transforms & the Convolution Theorem
    Convolution, Correlation, & Fourier Transforms James R. Graham 11/25/2009 Introduction • A large class of signal processing techniques fall under the category of Fourier transform methods – These methods fall into two broad categories • Efficient method for accomplishing common data manipulations • Problems related to the Fourier transform or the power spectrum Time & Frequency Domains • A physical process can be described in two ways – In the time domain, by h as a function of time t, that is h(t), -∞ < t < ∞ – In the frequency domain, by H that gives its amplitude and phase as a function of frequency f, that is H(f), with -∞ < f < ∞ • In general h and H are complex numbers • It is useful to think of h(t) and H(f) as two different representations of the same function – One goes back and forth between these two representations by Fourier transforms Fourier Transforms ∞ H( f )= ∫ h(t)e−2πift dt −∞ ∞ h(t)= ∫ H ( f )e2πift df −∞ • If t is measured in seconds, then f is in cycles per second or Hz • Other units – E.g, if h=h(x) and x is in meters, then H is a function of spatial frequency measured in cycles per meter Fourier Transforms • The Fourier transform is a linear operator – The transform of the sum of two functions is the sum of the transforms h12 = h1 + h2 ∞ H ( f ) h e−2πift dt 12 = ∫ 12 −∞ ∞ ∞ ∞ h h e−2πift dt h e−2πift dt h e−2πift dt = ∫ ( 1 + 2 ) = ∫ 1 + ∫ 2 −∞ −∞ −∞ = H1 + H 2 Fourier Transforms • h(t) may have some special properties – Real, imaginary – Even: h(t) = h(-t) – Odd: h(t) = -h(-t) • In the frequency domain these
    [Show full text]
  • STATISTICAL FOURIER ANALYSIS: CLARIFICATIONS and INTERPRETATIONS by DSG Pollock
    STATISTICAL FOURIER ANALYSIS: CLARIFICATIONS AND INTERPRETATIONS by D.S.G. Pollock (University of Leicester) Email: stephen [email protected] This paper expounds some of the results of Fourier theory that are es- sential to the statistical analysis of time series. It employs the algebra of circulant matrices to expose the structure of the discrete Fourier transform and to elucidate the filtering operations that may be applied to finite data sequences. An ideal filter with a gain of unity throughout the pass band and a gain of zero throughout the stop band is commonly regarded as incapable of being realised in finite samples. It is shown here that, to the contrary, such a filter can be realised both in the time domain and in the frequency domain. The algebra of circulant matrices is also helpful in revealing the nature of statistical processes that are band limited in the frequency domain. In order to apply the conventional techniques of autoregressive moving-average modelling, the data generated by such processes must be subjected to anti- aliasing filtering and sub sampling. These techniques are also described. It is argued that band-limited processes are more prevalent in statis- tical and econometric time series than is commonly recognised. 1 D.S.G. POLLOCK: Statistical Fourier Analysis 1. Introduction Statistical Fourier analysis is an important part of modern time-series analysis, yet it frequently poses an impediment that prevents a full understanding of temporal stochastic processes and of the manipulations to which their data are amenable. This paper provides a survey of the theory that is not overburdened by inessential complications, and it addresses some enduring misapprehensions.
    [Show full text]
  • Fourier Transform, Convolution Theorem, and Linear Dynamical Systems April 28, 2016
    Mathematical Tools for Neuroscience (NEU 314) Princeton University, Spring 2016 Jonathan Pillow Lecture 23: Fourier Transform, Convolution Theorem, and Linear Dynamical Systems April 28, 2016. Discrete Fourier Transform (DFT) We will focus on the discrete Fourier transform, which applies to discretely sampled signals (i.e., vectors). Linear algebra provides a simple way to think about the Fourier transform: it is simply a change of basis, specifically a mapping from the time domain to a representation in terms of a weighted combination of sinusoids of different frequencies. The discrete Fourier transform is therefore equiv- alent to multiplying by an orthogonal (or \unitary", which is the same concept when the entries are complex-valued) matrix1. For a vector of length N, the matrix that performs the DFT (i.e., that maps it to a basis of sinusoids) is an N × N matrix. The k'th row of this matrix is given by exp(−2πikt), for k 2 [0; :::; N − 1] (where we assume indexing starts at 0 instead of 1), and t is a row vector t=0:N-1;. Recall that exp(iθ) = cos(θ) + i sin(θ), so this gives us a compact way to represent the signal with a linear superposition of sines and cosines. The first row of the DFT matrix is all ones (since exp(0) = 1), and so the first element of the DFT corresponds to the sum of the elements of the signal. It is often known as the \DC component". The next row is a complex sinusoid that completes one cycle over the length of the signal, and each subsequent row has a frequency that is an integer multiple of this \fundamental" frequency.
    [Show full text]
  • A Hilbert Space Theory of Generalized Graph Signal Processing
    1 A Hilbert Space Theory of Generalized Graph Signal Processing Feng Ji and Wee Peng Tay, Senior Member, IEEE Abstract Graph signal processing (GSP) has become an important tool in many areas such as image pro- cessing, networking learning and analysis of social network data. In this paper, we propose a broader framework that not only encompasses traditional GSP as a special case, but also includes a hybrid framework of graph and classical signal processing over a continuous domain. Our framework relies extensively on concepts and tools from functional analysis to generalize traditional GSP to graph signals in a separable Hilbert space with infinite dimensions. We develop a concept analogous to Fourier transform for generalized GSP and the theory of filtering and sampling such signals. Index Terms Graph signal proceesing, Hilbert space, generalized graph signals, F-transform, filtering, sampling I. INTRODUCTION Since its emergence, the theory and applications of graph signal processing (GSP) have rapidly developed (see for example, [1]–[10]). Traditional GSP theory is essentially based on a change of orthonormal basis in a finite dimensional vector space. Suppose G = (V; E) is a weighted, arXiv:1904.11655v2 [eess.SP] 16 Sep 2019 undirected graph with V the vertex set of size n and E the set of edges. Recall that a graph signal f assigns a complex number to each vertex, and hence f can be regarded as an element of n C , where C is the set of complex numbers. The heart of the theory is a shift operator AG that is usually defined using a property of the graph.
    [Show full text]
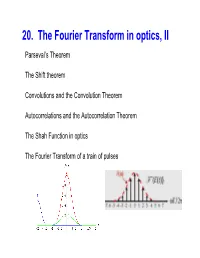
  • 20. the Fourier Transform in Optics, II Parseval’S Theorem
    20. The Fourier Transform in optics, II Parseval’s Theorem The Shift theorem Convolutions and the Convolution Theorem Autocorrelations and the Autocorrelation Theorem The Shah Function in optics The Fourier Transform of a train of pulses The spectrum of a light wave The spectrum of a light wave is defined as: 2 SFEt {()} where F{E(t)} denotes E(), the Fourier transform of E(t). The Fourier transform of E(t) contains the same information as the original function E(t). The Fourier transform is just a different way of representing a signal (in the frequency domain rather than in the time domain). But the spectrum contains less information, because we take the magnitude of E(), therefore losing the phase information. Parseval’s Theorem Parseval’s Theorem* says that the 221 energy in a function is the same, whether f ()tdt F ( ) d 2 you integrate over time or frequency: Proof: f ()tdt2 f ()t f *()tdt 11 F( exp(j td ) F *( exp(j td ) dt 22 11 FF() *(') exp([j '])tdtd ' d 22 11 FF( ) * ( ') [2 ')] dd ' 22 112 FF() *() d F () d * also known as 22Rayleigh’s Identity. The Fourier Transform of a sum of two f(t) F() functions t g(t) G() Faft() bgt () aF ft() bFgt () t The FT of a sum is the F() + sum of the FT’s. f(t)+g(t) G() Also, constants factor out. t This property reflects the fact that the Fourier transform is a linear operation. Shift Theorem The Fourier transform of a shifted function, f ():ta Ffta ( ) exp( jaF ) ( ) Proof : This theorem is F ft a ft( a )exp( jtdt ) important in optics, because we often encounter functions Change variables : uta that are shifting (continuously) along fu( )exp( j [ u a ]) du the time axis – they are called waves! exp(ja ) fu ( )exp( judu ) exp(jaF ) ( ) QED An example of the Shift Theorem in optics Suppose that we’re measuring the spectrum of a light wave, E(t), but a small fraction of the irradiance of this light, say , takes a different path that also leads to the spectrometer.
    [Show full text]
  • The Fourier Transform
    The Fourier Transform CS/CME/BIOPHYS/BMI 279 Fall 2015 Ron Dror The Fourier transform is a mathematical method that expresses a function as the sum of sinusoidal functions (sine waves). Fourier transforms are widely used in many fields of sciences and engineering, including image processing, quantum mechanics, crystallography, geoscience, etc. Here we will use, as examples, functions with finite, discrete domains (i.e., functions defined at a finite number of regularly spaced points), as typically encountered in computational problems. However the concept of Fourier transform can be readily applied to functions with infinite or continuous domains. (We won’t differentiate between “Fourier series” and “Fourier transform.”) A graphical example ! ! Suppose we have a function � � defined in the range − < � < on 2� + 1 discrete points such that ! ! ! � = �. By a Fourier transform we aim to express it as: ! !!!! � �! = �! + �! cos 2��!� + �! + �! cos 2��!� + �! + ⋯ (1) We first demonstrate graphically how a function may be described by its Fourier components. Fig. 1 shows a function defined on 101 discrete data points integer � = −50, −49, … , 49, 50. In fig. 2, the first Fig. 1. The function to be Fourier transformed few Fourier components are plotted separately (left) and added together (right) to form an approximation to the original function. Finally, fig. 3 demonstrates that by including the components up to � = 50, a faithful representation of the original function can be obtained. � ��, �� & �� Single components Summing over components up to m 0 �! = 0.6 �! = 0 �! = 0 1 �! = 1.9 �! = 0.01 �! = 2.2 2 �! = 0.27 �! = 0.02 �! = −1.3 3 �! = 0.39 �! = 0.03 �! = 0.4 Fig.2.
    [Show full text]
  • Fourier Series, Haar Wavelets and Fast Fourier Transform
    FOURIER SERIES, HAAR WAVELETS AND FAST FOURIER TRANSFORM VESA KAARNIOJA, JESSE RAILO AND SAMULI SILTANEN Abstract. This handout is for the course Applications of matrix computations at the University of Helsinki in Spring 2018. We recall basic algebra of complex numbers, define the Fourier series, the Haar wavelets and discrete Fourier transform, and describe the famous Fast Fourier Transform (FFT) algorithm. The discrete convolution is also considered. Contents 1. Revision on complex numbers 1 2. Fourier series 3 2.1. Fourier series: complex formulation 5 3. *Haar wavelets 5 3.1. *Theoretical approach as an orthonormal basis of L2([0, 1]) 6 4. Discrete Fourier transform 7 4.1. *Discrete convolutions 10 5. Fast Fourier transform (FFT) 10 1. Revision on complex numbers A complex number is a pair x + iy := (x, y) ∈ C of x, y ∈ R. Let z = x + iy, w = a + ib ∈ C be two complex numbers. We define the sum as z + w := (x + a) + i(y + b) • Version 1. Suggestions and corrections could be send to jesse.railo@helsinki.fi. • Things labaled with * symbol are supposed to be extra material and might be more advanced. • There are some exercises in the text that are supposed to be relatively easy, even trivial, and support understanding of the main concepts. These are not part of the official course work. 1 2 VESA KAARNIOJA, JESSE RAILO AND SAMULI SILTANEN and the product as zw := (xa − yb) + i(ya + xb). These satisfy all the same algebraic rules as the real numbers. Recall and verify that i2 = −1. However, C is not an ordered field, i.e.
    [Show full text]
  • MATLAB Examples Mathematics
    MATLAB Examples Mathematics Hans-Petter Halvorsen, M.Sc. Mathematics with MATLAB • MATLAB is a powerful tool for mathematical calculations. • Type “help elfun” (elementary math functions) in the Command window for more information about basic mathematical functions. Mathematics Topics • Basic Math Functions and Expressions � = 3�% + ) �% + �% + �+,(.) • Statistics – mean, median, standard deviation, minimum, maximum and variance • Trigonometric Functions sin() , cos() , tan() • Complex Numbers � = � + �� • Polynomials = =>< � � = �<� + �%� + ⋯ + �=� + �=@< Basic Math Functions Create a function that calculates the following mathematical expression: � = 3�% + ) �% + �% + �+,(.) We will test with different values for � and � We create the function: function z=calcexpression(x,y) z=3*x^2 + sqrt(x^2+y^2)+exp(log(x)); Testing the function gives: >> x=2; >> y=2; >> calcexpression(x,y) ans = 16.8284 Statistics Functions • MATLAB has lots of built-in functions for Statistics • Create a vector with random numbers between 0 and 100. Find the following statistics: mean, median, standard deviation, minimum, maximum and the variance. >> x=rand(100,1)*100; >> mean(x) >> median(x) >> std(x) >> mean(x) >> min(x) >> max(x) >> var(x) Trigonometric functions sin(�) cos(�) tan(�) Trigonometric functions It is quite easy to convert from radians to degrees or from degrees to radians. We have that: 2� ������� = 360 ������� This gives: 180 � ������� = �[�������] M � � �[�������] = �[�������] M 180 → Create two functions that convert from radians to degrees (r2d(x)) and from degrees to radians (d2r(x)) respectively. Test the functions to make sure that they work as expected. The functions are as follows: function d = r2d(r) d=r*180/pi; function r = d2r(d) r=d*pi/180; Testing the functions: >> r2d(2*pi) ans = 360 >> d2r(180) ans = 3.1416 Trigonometric functions Given right triangle: • Create a function that finds the angle A (in degrees) based on input arguments (a,c), (b,c) and (a,b) respectively.
    [Show full text]