DOCSLIB.ORG

A Hilbert Space Theory of Generalized Graph Signal Processing

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Hilbert Space Theory of Generalized Graph Signal Processing 1 A Hilbert Space Theory of Generalized Graph Signal Processing Feng Ji and Wee Peng Tay, Senior Member, IEEE Abstract Graph signal processing (GSP) has become an important tool in many areas such as image pro- cessing, networking learning and analysis of social network data. In this paper, we propose a broader framework that not only encompasses traditional GSP as a special case, but also includes a hybrid framework of graph and classical signal processing over a continuous domain. Our framework relies extensively on concepts and tools from functional analysis to generalize traditional GSP to graph signals in a separable Hilbert space with infinite dimensions. We develop a concept analogous to Fourier transform for generalized GSP and the theory of filtering and sampling such signals. Index Terms Graph signal proceesing, Hilbert space, generalized graph signals, F-transform, filtering, sampling I. INTRODUCTION Since its emergence, the theory and applications of graph signal processing (GSP) have rapidly developed (see for example, [1]–[10]). Traditional GSP theory is essentially based on a change of orthonormal basis in a finite dimensional vector space. Suppose G = (V; E) is a weighted, arXiv:1904.11655v2 [eess.SP] 16 Sep 2019 undirected graph with V the vertex set of size n and E the set of edges. Recall that a graph signal f assigns a complex number to each vertex, and hence f can be regarded as an element of n C , where C is the set of complex numbers. The heart of the theory is a shift operator AG that is usually defined using a property of the graph. Examples of AG include the adjacency matrix and the Laplacian matrix of G. Graph shift operators are typically chosen to be symmetric. By the This research is supported by the Singapore Ministry of Education Academic Research Fund Tier 2 grant MOE2018-T2-2-019. The authors are with the School of Electrical and Electronic Engineering, Nanyang Technological University, Singapore (e-mail: [email protected], [email protected]). 2 n spectral theorem, all the eigenvalues of AG are real and C has an orthonormal basis consisting of eigenvectors of AG. Therefore, one can define the notion of vertex and frequency domains, on which the rest of the theory builds upon. However, instead of assigning a complex number at each vertex, one can assign mathematical objects with richer structures to each vertex of a graph. An example of such a mathematical object comes from a Hilbert space. In particular, it would be of interest to assign an L2 function over a finite closed interval [a; b] to each vertex of a graph. Such a consideration is not just a plain generalization, as it has important practical applications in for example, sensor networks and social networks, where each node in the network is observing a time-varying continuous signal. We have the following considerations. Example 1. (a) The case where each vertex signal is a complex number belongs to the traditional GSP framework, which has been extensively studied in [1]–[10]. (b) An extension of traditional GSP to the case where each vertex signal is a finite-length discrete time series is proposed in the time-vertex GSP framework [8]. Such a vertex signal is from a Hilbert space Cm for some m ≥ 1. The assumption here is that all the time series at different vertices share the same time indices. (c) The case where the signal at each graph vertex v 2 V is itself a graph signal on a finite graph Gv has not been studied in the literature, to the best of our knowledge. In this case, each vertex signal is from Cm for some m ≥ 1, but unlike the time-vertex GSP framework, the underlying graph topology can be more general (the time-vertex GSP framework is equivalent to using a path graph with m vertices). Furthermore, different vertices can have different underlying graphs for their signals, and the correspondence between the vertices in Gv and those in Gu for v 6= u need not be one-to-one. Applications include relating the signals in one social network to another social network, or in problems where the underlying graph at each vertex of G is varying (cf. Section VI-D). For example, when studying signals on time-varying adaptive networks ( [11]–[14]), which includes social networks, biological networks and neural networks, we may let G be a path graph representing a finite portion of the time line. The signal ft at each node t is a vector in Cm. Due to the additional local structures in the signal, it is usually advantageous to consider these structures when performing signal analysis. Thus, we can regard ft as a 3 graph signal corresponding to time t. Furthermore, multiple graph signals ft from different networks can be related to each other, forming yet another underlying graph at each time t. (d) The case where the signal at each vertex is drawn from an infinite dimensional Hilbert space has again never been studied. An example is continuous time signals that are not bandlimited (in the time direction). In this case, from the Shannon-Nyquist Theorem [15], it is impossible to recover the full undistorted signal using a finite sampling rate (cf. Section VI-B). Thus, the time-vertex GSP framework, which requires discrete time series at all graph vertice, would introduce errors in the inference procedure. Furthermore, signals may not be sampled synchronously in a sensor network (sensor synchronization usually requires additional effort [16]–[18]) so that the time-vertex GSP framework may not be the best approach. A more general GSP framework is thus needed to address many practical engineering scenarios. In addition, a Hilbert space, such as the space of L2 functions over an appropriate domain Ω, usually has rich internal structures. The usual GSP framework takes a “snapshot picture" by looking at the graph signal at x 2 Ω one by one. This approach may easily disregard the internal relations among the points in Ω. In this paper, the proposed framework avoids such a local consideration entirely, and fuses the graph operators with operations on L2(Ω) for signal processing to achieve minimal information loss. For example, to study continuous time graph signals mentioned above, it can be more beneficial to consider the graph signal to be a function belonging to L2(R), such that we may apply operations such as continuous Fourier transform and wavelet transforms in conjunction with graph based transforms. We shall demonstrate this by the example of information propagation on social networks in Section VI-B. In this paper, we propose and develop a Hilbert space theory of generalized GSP that can handle all the above cases. To do that, it is inevitable that the theory is based on an abstract foundation, which requires the reader to have a good grasp of functional analysis concepts and tools. For these, we refer the reader to [19], [20]. We shall constantly refer back to Example 1 to illustrate and explain theoretical results. We shall develop the theory parallel to classical signal processing and GSP. Important notions such as convolution filters and bandlimitedness are best understood when signals are viewed in the frequency domain. Therefore, defining what constitutes the frequency domain is a hallmark of both classical signal processing and traditional GSP. In the same spirit, we first define the 4 frequency domain for the generalized GSP framework using the spectral theory of compact operators on Hilbert spaces. We then proceed to discuss filtering and sampling. A preliminary version of this paper was presented in the conference paper [21], which introduced some of the basic concepts in this paper without proof. The rest of the paper is organized as follows. In Section II, we set up the framework by defining graph signals in a separable Hilbert space. In Section III, we introduce the notion of frequency. Based on this, we develop the concepts of filtering and sampling in Section IV and Section V. We present numerical results in Section VI and conclude in Section VII. Throughout, we provide examples to highlight situations where the framework of the paper is not only applicable but also necessary. Notations. We use R and C to denote the real and complex fields, respectively, while Z denotes the set of integers. The symbol ⊗ denotes tensor product, ◦ is function composition, and ∼= p denotes isomorphic equivalence. Id is the identity operator and i = −1. Cn is equipped with 2 2 an inner product h·; ·i n with corresponding norm k·k n . The space L (Ω) = L (Ω; F; µ) with C C R 2 (Ω; F; µ) a measure space, is the collection of functions f :Ω 7! C such that Ω jfj dµ < 1. II. GENERALIZED GRAPH SIGNALS Let G = (V; E) be a simple finite undirected weighted graph and X be a metric space. In this paper, when we talk about a vector space, we always assume that the base field is the complex numbers C, unless otherwise stated. In traditional GSP, the signals on the vertices of G are assumed to be real or complex. We generalize this as follows. Definition 1. Suppose H is a Hilbert space (i.e., a complete inner product space). A graph signal in H is a function f : V !H: The space of graph signals in H is denoted by S(G; H): With a few examples below, we demonstrate why this generalized notion is versatile. In short, Hilbert spaces include both the more familiar finite dimensional cases and also infinite dimensional cases that can represent more realistic signals in practice.
Load more

Recommended publications
  • Uniform Boundedness Principle for Unbounded Operators
    UNIFORM BOUNDEDNESS PRINCIPLE FOR UNBOUNDED OPERATORS C. GANESA MOORTHY and CT. RAMASAMY Abstract. A uniform boundedness principle for unbounded operators is derived. A particular case is: Suppose fTigi2I is a family of linear mappings of a Banach space X into a normed space Y such that fTix : i 2 Ig is bounded for each x 2 X; then there exists a dense subset A of the open unit ball in X such that fTix : i 2 I; x 2 Ag is bounded. A closed graph theorem and a bounded inverse theorem are obtained for families of linear mappings as consequences of this principle. Some applications of this principle are also obtained. 1. Introduction There are many forms for uniform boundedness principle. There is no known evidence for this principle for unbounded operators which generalizes classical uniform boundedness principle for bounded operators. The second section presents a uniform boundedness principle for unbounded operators. An application to derive Hellinger-Toeplitz theorem is also obtained in this section. A JJ J I II closed graph theorem and a bounded inverse theorem are obtained for families of linear mappings in the third section as consequences of this principle. Go back Let us assume the following: Every vector space X is over R or C. An α-seminorm (0 < α ≤ 1) is a mapping p: X ! [0; 1) such that p(x + y) ≤ p(x) + p(y), p(ax) ≤ jajαp(x) for all x; y 2 X Full Screen Close Received November 7, 2013. 2010 Mathematics Subject Classification. Primary 46A32, 47L60. Key words and phrases.
    [Show full text]
  • On the Boundary Between Mereology and Topology
    On the Boundary Between Mereology and Topology Achille C. Varzi Istituto per la Ricerca Scientifica e Tecnologica, I-38100 Trento, Italy [email protected] (Final version published in Roberto Casati, Barry Smith, and Graham White (eds.), Philosophy and the Cognitive Sciences. Proceedings of the 16th International Wittgenstein Symposium, Vienna, Hölder-Pichler-Tempsky, 1994, pp. 423–442.) 1. Introduction Much recent work aimed at providing a formal ontology for the common-sense world has emphasized the need for a mereological account to be supplemented with topological concepts and principles. There are at least two reasons under- lying this view. The first is truly metaphysical and relates to the task of charac- terizing individual integrity or organic unity: since the notion of connectedness runs afoul of plain mereology, a theory of parts and wholes really needs to in- corporate a topological machinery of some sort. The second reason has been stressed mainly in connection with applications to certain areas of artificial in- telligence, most notably naive physics and qualitative reasoning about space and time: here mereology proves useful to account for certain basic relation- ships among things or events; but one needs topology to account for the fact that, say, two events can be continuous with each other, or that something can be inside, outside, abutting, or surrounding something else. These motivations (at times combined with others, e.g., semantic transpar- ency or computational efficiency) have led to the development of theories in which both mereological and topological notions play a pivotal role. How ex- actly these notions are related, however, and how the underlying principles should interact with one another, is still a rather unexplored issue.
    [Show full text]
  • Baire Category Theorem and Uniform Boundedness Principle)
    Functional Analysis (WS 19/20), Problem Set 3 (Baire Category Theorem and Uniform Boundedness Principle) Baire Category Theorem B1. Let (X; k·kX ) be an innite dimensional Banach space. Prove that X has uncountable Hamel basis. Note: This is Problem A2 from Problem Set 1. B2. Consider subset of bounded sequences 1 A = fx 2 l : only nitely many xk are nonzerog : Can one dene a norm on A so that it becomes a Banach space? Consider the same question with the set of polynomials dened on interval [0; 1]. B3. Prove that the set L2(0; 1) has empty interior as the subset of Banach space L1(0; 1). B4. Let f : [0; 1) ! [0; 1) be a continuous function such that for every x 2 [0; 1), f(kx) ! 0 as k ! 1. Prove that f(x) ! 0 as x ! 1. B5.( Uniform Boundedness Principle) Let (X; k · kX ) be a Banach space and (Y; k · kY ) be a normed space. Let fTαgα2A be a family of bounded linear operators between X and Y . Suppose that for any x 2 X, sup kTαxkY < 1: α2A Prove that . supα2A kTαk < 1 Uniform Boundedness Principle U1. Let F be a normed space C[0; 1] with L2(0; 1) norm. Check that the formula 1 Z n 'n(f) = n f(t) dt 0 denes a bounded linear functional on . Verify that for every , F f 2 F supn2N j'n(f)j < 1 but . Why Uniform Boundedness Principle is not satised in this case? supn2N k'nk = 1 U2.( pointwise convergence of operators) Let (X; k · kX ) be a Banach space and (Y; k · kY ) be a normed space.
    [Show full text]
  • FUNCTIONAL ANALYSIS 1. Banach and Hilbert Spaces in What
    FUNCTIONAL ANALYSIS PIOTR HAJLASZ 1. Banach and Hilbert spaces In what follows K will denote R of C. Definition. A normed space is a pair (X, k · k), where X is a linear space over K and k · k : X → [0, ∞) is a function, called a norm, such that (1) kx + yk ≤ kxk + kyk for all x, y ∈ X; (2) kαxk = |α|kxk for all x ∈ X and α ∈ K; (3) kxk = 0 if and only if x = 0. Since kx − yk ≤ kx − zk + kz − yk for all x, y, z ∈ X, d(x, y) = kx − yk defines a metric in a normed space. In what follows normed paces will always be regarded as metric spaces with respect to the metric d. A normed space is called a Banach space if it is complete with respect to the metric d. Definition. Let X be a linear space over K (=R or C). The inner product (scalar product) is a function h·, ·i : X × X → K such that (1) hx, xi ≥ 0; (2) hx, xi = 0 if and only if x = 0; (3) hαx, yi = αhx, yi; (4) hx1 + x2, yi = hx1, yi + hx2, yi; (5) hx, yi = hy, xi, for all x, x1, x2, y ∈ X and all α ∈ K. As an obvious corollary we obtain hx, y1 + y2i = hx, y1i + hx, y2i, hx, αyi = αhx, yi , Date: February 12, 2009. 1 2 PIOTR HAJLASZ for all x, y1, y2 ∈ X and α ∈ K. For a space with an inner product we define kxk = phx, xi . Lemma 1.1 (Schwarz inequality).
    [Show full text]
  • FOURIER TRANSFORM Very Broadly Speaking, the Fourier Transform Is a Systematic Way to Decompose “Generic” Functions Into
    FOURIER TRANSFORM TERENCE TAO Very broadly speaking, the Fourier transform is a systematic way to decompose “generic” functions into a superposition of “symmetric” functions. These symmetric functions are usually quite explicit (such as a trigonometric function sin(nx) or cos(nx)), and are often associated with physical concepts such as frequency or energy. What “symmetric” means here will be left vague, but it will usually be associated with some sort of group G, which is usually (though not always) abelian. Indeed, the Fourier transform is a fundamental tool in the study of groups (and more precisely in the representation theory of groups, which roughly speaking describes how a group can define a notion of symmetry). The Fourier transform is also related to topics in linear algebra, such as the representation of a vector as linear combinations of an orthonormal basis, or as linear combinations of eigenvectors of a matrix (or a linear operator). To give a very simple prototype of the Fourier transform, consider a real-valued function f : R → R. Recall that such a function f(x) is even if f(−x) = f(x) for all x ∈ R, and is odd if f(−x) = −f(x) for all x ∈ R. A typical function f, such as f(x) = x3 + 3x2 + 3x + 1, will be neither even nor odd. However, one can always write f as the superposition f = fe + fo of an even function fe and an odd function fo by the formulae f(x) + f(−x) f(x) − f(−x) f (x) := ; f (x) := . e 2 o 2 3 2 2 3 For instance, if f(x) = x + 3x + 3x + 1, then fe(x) = 3x + 1 and fo(x) = x + 3x.
    [Show full text]
  • An Introduction to Fourier Analysis Fourier Series, Partial Differential Equations and Fourier Transforms
    An Introduction to Fourier Analysis Fourier Series, Partial Differential Equations and Fourier Transforms Notes prepared for MA3139 Arthur L. Schoenstadt Department of Applied Mathematics Naval Postgraduate School Code MA/Zh Monterey, California 93943 August 18, 2005 c 1992 - Professor Arthur L. Schoenstadt 1 Contents 1 Infinite Sequences, Infinite Series and Improper Integrals 1 1.1Introduction.................................... 1 1.2FunctionsandSequences............................. 2 1.3Limits....................................... 5 1.4TheOrderNotation................................ 8 1.5 Infinite Series . ................................ 11 1.6ConvergenceTests................................ 13 1.7ErrorEstimates.................................. 15 1.8SequencesofFunctions.............................. 18 2 Fourier Series 25 2.1Introduction.................................... 25 2.2DerivationoftheFourierSeriesCoefficients.................. 26 2.3OddandEvenFunctions............................. 35 2.4ConvergencePropertiesofFourierSeries.................... 40 2.5InterpretationoftheFourierCoefficients.................... 48 2.6TheComplexFormoftheFourierSeries.................... 53 2.7FourierSeriesandOrdinaryDifferentialEquations............... 56 2.8FourierSeriesandDigitalDataTransmission.................. 60 3 The One-Dimensional Wave Equation 70 3.1Introduction.................................... 70 3.2TheOne-DimensionalWaveEquation...................... 70 3.3 Boundary Conditions ............................... 76 3.4InitialConditions................................
    [Show full text]
  • A Study of Optimization in Hilbert Space
    California State University, San Bernardino CSUSB ScholarWorks Theses Digitization Project John M. Pfau Library 1998 A study of optimization in Hilbert Space John Awunganyi Follow this and additional works at: https://scholarworks.lib.csusb.edu/etd-project Part of the Mathematics Commons Recommended Citation Awunganyi, John, "A study of optimization in Hilbert Space" (1998). Theses Digitization Project. 1459. https://scholarworks.lib.csusb.edu/etd-project/1459 This Project is brought to you for free and open access by the John M. Pfau Library at CSUSB ScholarWorks. It has been accepted for inclusion in Theses Digitization Project by an authorized administrator of CSUSB ScholarWorks. For more information, please contact [email protected]. A STUDY OF OPTIMIZATIONIN HELBERT SPACE A Project Presented to the Faculty of California State University, San Bernardino In Partial Fulfillment ofthe Requirements for the Degree Master ofArts in Mathematics by John Awunganyi June 1998 A STUDY OF OPTIMIZATION IN HILBERT SPACE A Project Presented to the Faculty of California State University, San Bernardino by John Awunganyi June 1998 Approved by; Dr. Chetan Prakash, Chair, Mathematics Date r. Wenxang Wang Dr. Christopher Freiling Dr. Terry Hallett, Graduate Coordinator Dr. Peter Williams, Department Chair ABSTRACT The primary objective ofthis project is to demonstrate that a certain field ofoptimization can be effectively unified by afew geometric principles ofcomplete normed linear space theory. By employing these principles, important and complex finite - dimensional problems can be interpreted and solved by methods springing from geometric insight. Concepts such as distance, orthogonality, and convexity play a fundamental and indispensable role in this development. Viewed in these terms, seemingly diverse problems and techniques often are found to be closely related.
    [Show full text]
  • Fourier Transforms & the Convolution Theorem
    Convolution, Correlation, & Fourier Transforms James R. Graham 11/25/2009 Introduction • A large class of signal processing techniques fall under the category of Fourier transform methods – These methods fall into two broad categories • Efficient method for accomplishing common data manipulations • Problems related to the Fourier transform or the power spectrum Time & Frequency Domains • A physical process can be described in two ways – In the time domain, by h as a function of time t, that is h(t), -∞ < t < ∞ – In the frequency domain, by H that gives its amplitude and phase as a function of frequency f, that is H(f), with -∞ < f < ∞ • In general h and H are complex numbers • It is useful to think of h(t) and H(f) as two different representations of the same function – One goes back and forth between these two representations by Fourier transforms Fourier Transforms ∞ H( f )= ∫ h(t)e−2πift dt −∞ ∞ h(t)= ∫ H ( f )e2πift df −∞ • If t is measured in seconds, then f is in cycles per second or Hz • Other units – E.g, if h=h(x) and x is in meters, then H is a function of spatial frequency measured in cycles per meter Fourier Transforms • The Fourier transform is a linear operator – The transform of the sum of two functions is the sum of the transforms h12 = h1 + h2 ∞ H ( f ) h e−2πift dt 12 = ∫ 12 −∞ ∞ ∞ ∞ h h e−2πift dt h e−2πift dt h e−2πift dt = ∫ ( 1 + 2 ) = ∫ 1 + ∫ 2 −∞ −∞ −∞ = H1 + H 2 Fourier Transforms • h(t) may have some special properties – Real, imaginary – Even: h(t) = h(-t) – Odd: h(t) = -h(-t) • In the frequency domain these
    [Show full text]
  • STATISTICAL FOURIER ANALYSIS: CLARIFICATIONS and INTERPRETATIONS by DSG Pollock
    STATISTICAL FOURIER ANALYSIS: CLARIFICATIONS AND INTERPRETATIONS by D.S.G. Pollock (University of Leicester) Email: stephen [email protected] This paper expounds some of the results of Fourier theory that are es- sential to the statistical analysis of time series. It employs the algebra of circulant matrices to expose the structure of the discrete Fourier transform and to elucidate the filtering operations that may be applied to finite data sequences. An ideal filter with a gain of unity throughout the pass band and a gain of zero throughout the stop band is commonly regarded as incapable of being realised in finite samples. It is shown here that, to the contrary, such a filter can be realised both in the time domain and in the frequency domain. The algebra of circulant matrices is also helpful in revealing the nature of statistical processes that are band limited in the frequency domain. In order to apply the conventional techniques of autoregressive moving-average modelling, the data generated by such processes must be subjected to anti- aliasing filtering and sub sampling. These techniques are also described. It is argued that band-limited processes are more prevalent in statis- tical and econometric time series than is commonly recognised. 1 D.S.G. POLLOCK: Statistical Fourier Analysis 1. Introduction Statistical Fourier analysis is an important part of modern time-series analysis, yet it frequently poses an impediment that prevents a full understanding of temporal stochastic processes and of the manipulations to which their data are amenable. This paper provides a survey of the theory that is not overburdened by inessential complications, and it addresses some enduring misapprehensions.
    [Show full text]
  • Fourier Transform, Convolution Theorem, and Linear Dynamical Systems April 28, 2016
    Mathematical Tools for Neuroscience (NEU 314) Princeton University, Spring 2016 Jonathan Pillow Lecture 23: Fourier Transform, Convolution Theorem, and Linear Dynamical Systems April 28, 2016. Discrete Fourier Transform (DFT) We will focus on the discrete Fourier transform, which applies to discretely sampled signals (i.e., vectors). Linear algebra provides a simple way to think about the Fourier transform: it is simply a change of basis, specifically a mapping from the time domain to a representation in terms of a weighted combination of sinusoids of different frequencies. The discrete Fourier transform is therefore equiv- alent to multiplying by an orthogonal (or \unitary", which is the same concept when the entries are complex-valued) matrix1. For a vector of length N, the matrix that performs the DFT (i.e., that maps it to a basis of sinusoids) is an N × N matrix. The k'th row of this matrix is given by exp(−2πikt), for k 2 [0; :::; N − 1] (where we assume indexing starts at 0 instead of 1), and t is a row vector t=0:N-1;. Recall that exp(iθ) = cos(θ) + i sin(θ), so this gives us a compact way to represent the signal with a linear superposition of sines and cosines. The first row of the DFT matrix is all ones (since exp(0) = 1), and so the first element of the DFT corresponds to the sum of the elements of the signal. It is often known as the \DC component". The next row is a complex sinusoid that completes one cycle over the length of the signal, and each subsequent row has a frequency that is an integer multiple of this \fundamental" frequency.
    [Show full text]
  • 20. the Fourier Transform in Optics, II Parseval’S Theorem
    20. The Fourier Transform in optics, II Parseval’s Theorem The Shift theorem Convolutions and the Convolution Theorem Autocorrelations and the Autocorrelation Theorem The Shah Function in optics The Fourier Transform of a train of pulses The spectrum of a light wave The spectrum of a light wave is defined as: 2 SFEt {()} where F{E(t)} denotes E(), the Fourier transform of E(t). The Fourier transform of E(t) contains the same information as the original function E(t). The Fourier transform is just a different way of representing a signal (in the frequency domain rather than in the time domain). But the spectrum contains less information, because we take the magnitude of E(), therefore losing the phase information. Parseval’s Theorem Parseval’s Theorem* says that the 221 energy in a function is the same, whether f ()tdt F ( ) d 2 you integrate over time or frequency: Proof: f ()tdt2 f ()t f *()tdt 11 F( exp(j td ) F *( exp(j td ) dt 22 11 FF() *(') exp([j '])tdtd ' d 22 11 FF( ) * ( ') [2 ')] dd ' 22 112 FF() *() d F () d * also known as 22Rayleigh’s Identity. The Fourier Transform of a sum of two f(t) F() functions t g(t) G() Faft() bgt () aF ft() bFgt () t The FT of a sum is the F() + sum of the FT’s. f(t)+g(t) G() Also, constants factor out. t This property reflects the fact that the Fourier transform is a linear operation. Shift Theorem The Fourier transform of a shifted function, f ():ta Ffta ( ) exp( jaF ) ( ) Proof : This theorem is F ft a ft( a )exp( jtdt ) important in optics, because we often encounter functions Change variables : uta that are shifting (continuously) along fu( )exp( j [ u a ]) du the time axis – they are called waves! exp(ja ) fu ( )exp( judu ) exp(jaF ) ( ) QED An example of the Shift Theorem in optics Suppose that we’re measuring the spectrum of a light wave, E(t), but a small fraction of the irradiance of this light, say , takes a different path that also leads to the spectrometer.
    [Show full text]
  • The Fourier Transform
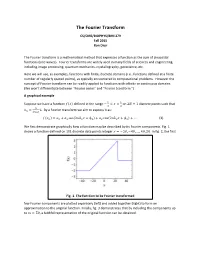
    The Fourier Transform CS/CME/BIOPHYS/BMI 279 Fall 2015 Ron Dror The Fourier transform is a mathematical method that expresses a function as the sum of sinusoidal functions (sine waves). Fourier transforms are widely used in many fields of sciences and engineering, including image processing, quantum mechanics, crystallography, geoscience, etc. Here we will use, as examples, functions with finite, discrete domains (i.e., functions defined at a finite number of regularly spaced points), as typically encountered in computational problems. However the concept of Fourier transform can be readily applied to functions with infinite or continuous domains. (We won’t differentiate between “Fourier series” and “Fourier transform.”) A graphical example ! ! Suppose we have a function � � defined in the range − < � < on 2� + 1 discrete points such that ! ! ! � = �. By a Fourier transform we aim to express it as: ! !!!! � �! = �! + �! cos 2��!� + �! + �! cos 2��!� + �! + ⋯ (1) We first demonstrate graphically how a function may be described by its Fourier components. Fig. 1 shows a function defined on 101 discrete data points integer � = −50, −49, … , 49, 50. In fig. 2, the first Fig. 1. The function to be Fourier transformed few Fourier components are plotted separately (left) and added together (right) to form an approximation to the original function. Finally, fig. 3 demonstrates that by including the components up to � = 50, a faithful representation of the original function can be obtained. � ��, �� & �� Single components Summing over components up to m 0 �! = 0.6 �! = 0 �! = 0 1 �! = 1.9 �! = 0.01 �! = 2.2 2 �! = 0.27 �! = 0.02 �! = −1.3 3 �! = 0.39 �! = 0.03 �! = 0.4 Fig.2.
    [Show full text]