Crystals and Crystal Structures
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Heat Treating Corundum: the Bangkok Operation
HEAT TREATING CORUNDUM: THE BANGKOK OPERATION By Jack S. D. Abraham Following LIP on Nassau's 1981 article on Banglzolz gem dealer buys a lo+-ct ruby for a six- the technical aspects of heat treating ruby A figure sum and heats it hoping to improve its color and sapphire, the author reports his and value. After one heating, the stone dulls and cannot personal observations of the actual heat be sold for half of its original price. But a few tries later treatment process in Bangkok. He the stone is so improved that a major European dealer discusses the potential effects that this buys it for almost five times the original amount- process can have on a stone-both positive and negative-and emphasizes lznowing that it has been heat treated. the importance of the natural make-up of Another Thai dealer pays a large sum for a 600-ct piece the stone itself to the success of heot of sapphire rough. He then cuts it into four sections and treatment. heats each. For the largest piece, which is over 100 ctl he receives 20% more than he paid for the entire original stone-again from a buyer who knows the stone is heated. A third dealer, however, heats a sapphire for which he has paid a six-figure sum but instead of enhancing the color, the treatment causes the stone to brealz into several pieces. It is now worth a fraction of its original price. Such incidents suggest that the heating of ruby and sapphire has become a fully acceptedl if very rislzyl fact of life in the Far East. -

SGG Corundum Treatment.Pptx
The beauty of colour © Swiss Gemmological Institute SSEF SGG Zentralkurs, Thun, 15. April 2013 Treatment of corundum characteristics, detection and declaration Michael S. Krzemnicki Swiss Gemmological Institute SSEF Switzerland Photos and figures © H.A. Hänni & M.S. Krzemnicki 1! Consumer+expectation+ Quality& Every&gemstone&deposit&produces&stones&of&high&and&low&quality.& Usually&the&quality&distribution&has&the&shape&of&a&pyramid.&& Top&stones&are&rare,&stones&of&lower&quality&are&very&abundant.& The&exploitation&of&gems&is&expensive,®ardless&of&their&quality.& It&is&economically&and&important&to&be&able&to&enhance&stones&of&& the&lower&part&of&the&quality&pyramid&(also&for&the&miners!)& Once&a&treatment&is&developed&and&successfull,&it&often&is&also&applied&& on&stones&of&better&quality&to&make&them&even&better&looking.& Gem$deposit+production+ Quantity& © SSEF Swiss Gemmological Institute Treatment options for corundum... To&modify&transparency:&& &F&Gilling&of&Gissures&with&colourless&substance&&(oil,&artiGicial&resin,&glass)& &F&heating&to&dissolve&inclusions& & To&modify&colour& &F&Gilling&of&Gissures&with&coloured&substance&(oil,&artiGicial&resin,&glass)& &F&heating&in&oxidising&or&reducing&conditions&(±&with&additives)& &F&diffusion&of&„colouring“&elements&into&the&corundum&lattice& &F&irradiation& & To&enhance&stability& &F&Gilling&of&Gissures/cavities&with&solidifyig&substances&& & To&create&optical&effects&& &F&heating&with&additives& & © SSEF Swiss Gemmological Institute! 2! Treatment options for corundum... Fissure&Gilling&and&dyeing& & Foiling,&Painting& Heating&with&blowFpipe& ©&F.&Notari& Heating&with&electrical&furnace& ©&H.A.&Hänni& Irradiation& Heating&combined&with&surface&diffusion& Heating&with&borax&to&induce&Gissure&„healing“& Beryllium&diffusion& LeadFglass&Gissure&Gilling& & CobaltFglass&Gissure&Gilling& & next&treatment&??& & future& 0& 1000& 1900& 2000& Time+scale+ & © SSEF Swiss Gemmological Institute! Treatment options for corundum.. -

Compilation of Reported Sapphire Occurrences in Montana
Report of Investigation 23 Compilation of Reported Sapphire Occurrences in Montana Richard B. Berg 2015 Cover photo by Richard Berg. Sapphires (very pale green and colorless) concentrated by panning. The small red grains are garnets, commonly found with sapphires in western Montana, and the black sand is mainly magnetite. Compilation of Reported Sapphire Occurrences, RI 23 Compilation of Reported Sapphire Occurrences in Montana Richard B. Berg Montana Bureau of Mines and Geology MBMG Report of Investigation 23 2015 i Compilation of Reported Sapphire Occurrences, RI 23 TABLE OF CONTENTS Introduction ............................................................................................................................1 Descriptions of Occurrences ..................................................................................................7 Selected Bibliography of Articles on Montana Sapphires ................................................... 75 General Montana ............................................................................................................75 Yogo ................................................................................................................................ 75 Southwestern Montana Alluvial Deposits........................................................................ 76 Specifi cally Rock Creek sapphire district ........................................................................ 76 Specifi cally Dry Cottonwood Creek deposit and the Butte area .................................... -

Mineral Collecting Sites in North Carolina by W
.'.' .., Mineral Collecting Sites in North Carolina By W. F. Wilson and B. J. McKenzie RUTILE GUMMITE IN GARNET RUBY CORUNDUM GOLD TORBERNITE GARNET IN MICA ANATASE RUTILE AJTUNITE AND TORBERNITE THULITE AND PYRITE MONAZITE EMERALD CUPRITE SMOKY QUARTZ ZIRCON TORBERNITE ~/ UBRAR'l USE ONLV ,~O NOT REMOVE. fROM LIBRARY N. C. GEOLOGICAL SUHVEY Information Circular 24 Mineral Collecting Sites in North Carolina By W. F. Wilson and B. J. McKenzie Raleigh 1978 Second Printing 1980. Additional copies of this publication may be obtained from: North CarOlina Department of Natural Resources and Community Development Geological Survey Section P. O. Box 27687 ~ Raleigh. N. C. 27611 1823 --~- GEOLOGICAL SURVEY SECTION The Geological Survey Section shall, by law"...make such exami nation, survey, and mapping of the geology, mineralogy, and topo graphy of the state, including their industrial and economic utilization as it may consider necessary." In carrying out its duties under this law, the section promotes the wise conservation and use of mineral resources by industry, commerce, agriculture, and other governmental agencies for the general welfare of the citizens of North Carolina. The Section conducts a number of basic and applied research projects in environmental resource planning, mineral resource explora tion, mineral statistics, and systematic geologic mapping. Services constitute a major portion ofthe Sections's activities and include identi fying rock and mineral samples submitted by the citizens of the state and providing consulting services and specially prepared reports to other agencies that require geological information. The Geological Survey Section publishes results of research in a series of Bulletins, Economic Papers, Information Circulars, Educa tional Series, Geologic Maps, and Special Publications. -

Zincite (Zn, Mn2+)O
Zincite (Zn, Mn2+)O c 2001-2005 Mineral Data Publishing, version 1 Crystal Data: Hexagonal. Point Group: 6mm. Crystals rare, typically pyramidal, hemimorphic, with large {0001}, to 2.5 cm, rarely curved; in broad cleavages, foliated, granular, compact, massive. Twinning: On {0001}, with composition plane {0001}. Physical Properties: Cleavage: {1010}, perfect; parting on {0001}, commonly distinct. Fracture: Conchoidal. Tenacity: Brittle. Hardness = 4 VHN = 205–221 (100 g load). D(meas.) = 5.66(2) D(calc.) = 5.6730 Rare pale yellow fluorescence under LW UV. Optical Properties: Translucent, transparent in thin fragments. Color: Yellow-orange to deep red, rarely yellow, green, colorless; deep red to yellow in transmitted light; light rose-brown in reflected light, with strong red to yellow internal reflections. Streak: Yellow-orange. Luster: Subadamantine to resinous. Optical Class: Uniaxial (+). ω = 2.013 = 2.029 R1–R2: (400) 13.0–13.6, (420) 12.8–13.2, (440) 12.6–12.8, (460) 12.3–12.6, (480) 12.1–12.4, (500) 12.0–12.2, (520) 11.8–12.1, (540) 11.8–12.0, (560) 11.7–11.9, (580) 11.6–11.8, (600) 11.4–11.7, (620) 11.3–11.6, (640) 11.2–11.5, (660) 11.1–11.4, (680) 11.0–11.2, (700) 11.0–11.2 Cell Data: Space Group: P 63mc (synthetic). a = 3.24992(5) c = 5.20658(8) Z = 2 X-ray Powder Pattern: Synthetic. 2.476 (100), 2.816 (71), 2.602 (56), 1.626 (40), 1.477 (35), 1.911 (29), 1.379 (28) Chemistry: (1) (2) SiO2 0.08 FeO 0.01 0.23 MnO 0.27 0.29 ZnO 99.63 98.88 Total 99.99 [99.40] (1) Sterling Hill, New Jersey, USA. -

Download the Scanned
American Mineralogist, Volume 70, pages 379-387, 1985 Ma_nganesehumites and leucophoenicitesfrom Franklin and Sterling- Hill' NewJersev: 'i"? andimplications ;ifi':il1,;;lfiil11"r's' Perr J. Dullx Department of Mineral Sciences Smithsonian lnstitution, Washington, D. C. 20560 Abstract The manganesehumites, (alleghanyite, manganhumite, and sonolite),together with some Mn-bearing samplesof the Mg-humites,and the related phasesleucophoenicite and jerry- gibbsite,from the orebodiesat Franklin and SterlingHill, New Jersey,are describedtogether with analytical data. Solid solution betweenhumite and manganhumiteis at least partially continuous. Expected Mn/Mg solid solutions between alleghanyiteand chondrodite, and betweensonolite and clinohumite, are discontinuous; they are interrupted by apparently orderedphases. In all cases,the possibleorderings involve Zn as well as Mn and Mg. There are no Mn end-membersof the manganesehumites at this locality. Manganeseis apparently restricted in leucophoenicite(5.42-6.63 Mn per 7 octahedral cations) and in jerrygibbsite (7.79-8.02Mn per 9 octahedralcations). Calcium is common to both leucophoeniciteand jerrygibbsite,but among the Mn-humites,only sonoliteaccepts appreciable Ca (0.65Ca per 9 octahedralcations). There is a "threshold" level ofzinc in all studiedsamples; this "threshold" levelis a constantfor leucophoenicite1-9.3 Znper 3 Si)and alleghanyite(-O.2Zn per 2 Si). No samplesof leucophoeniciteor jerrygibbsite were found to be Zn-ftee,suggesting either that Zn is required for their stability, or that these two phasesmight not be stable as end-members.Fluorine is present in all the Mn-humites and is proportional to the Mg- content,but is absentin leucophoeniciteand jerrygibbsite. Introduction humite speciesoccur there; the Mg-humites occur in the The magnesiumhumite species(norbergite, chondrodite, host Franklin Marble for the most part, and the Mn- humite, and clinohumite) have been well-studiedand re- humites in the orebodiesthemselves. -

A Review of the Structural Architecture of Tellurium Oxycompounds
Mineralogical Magazine, May 2016, Vol. 80(3), pp. 415–545 REVIEW OPEN ACCESS A review of the structural architecture of tellurium oxycompounds 1 2,* 3 A. G. CHRISTY ,S.J.MILLS AND A. R. KAMPF 1 Research School of Earth Sciences and Department of Applied Mathematics, Research School of Physics and Engineering, Australian National University, Canberra, ACT 2601, Australia 2 Geosciences, Museum Victoria, GPO Box 666, Melbourne, Victoria 3001, Australia 3 Mineral Sciences Department, Natural History Museum of Los Angeles County, 900 Exposition Boulevard, Los Angeles, CA 90007, USA [Received 24 November 2015; Accepted 23 February 2016; Associate Editor: Mark Welch] ABSTRACT Relative to its extremely low abundance in the Earth’s crust, tellurium is the most mineralogically diverse chemical element, with over 160 mineral species known that contain essential Te, many of them with unique crystal structures. We review the crystal structures of 703 tellurium oxysalts for which good refinements exist, including 55 that are known to occur as minerals. The dataset is restricted to compounds where oxygen is the only ligand that is strongly bound to Te, but most of the Periodic Table is represented in the compounds that are reviewed. The dataset contains 375 structures that contain only Te4+ cations and 302 with only Te6+, with 26 of the compounds containing Te in both valence states. Te6+ was almost exclusively in rather regular octahedral coordination by oxygen ligands, with only two instances each of 4- and 5-coordination. Conversely, the lone-pair cation Te4+ displayed irregular coordination, with a broad range of coordination numbers and bond distances. -

Leucophoenicite Mn (Sio4)3(OH)2
2+ Leucophoenicite Mn7 (SiO4)3(OH)2 c 2001 Mineral Data Publishing, version 1.2 ° Crystal Data: Monoclinic. Point Group: 2=m: Crystals rare, typically slender, prismatic, elongated and striated [010], to 8 mm; in isolated grains or granular massive. Twinning: On k 001 , common, contact or interpenetrant twins, lamellar. f g Physical Properties: Cleavage: 001 , imperfect. Tenacity: Brittle. Hardness = 5.5{6 f g D(meas.) = 3.848 D(calc.) = [4.01] Optical Properties: Transparent to translucent. Color: Brown to light purple-red, raspberry-red, deep pink to light pink; rose-red to colorless in thin section. Luster: Vitreous. Optical Class: Biaxial ({). Pleochroism: Faint; rose-red 001 ; colorless 001 . Orientation: k f g ? f g X 001 cleavage. Dispersion: r > v; slight. ® = 1.751(3) ¯ = 1.771(3) ° = 1.782(3) ? f g 2V(meas.) = 74(5)± Cell Data: Space Group: P 21=a: a = 10.842(19) b = 4.826(6) c = 11.324(9) ¯ = 103:93(9)± Z = [2] X-ray Powder Pattern: Franklin, New Jersey, USA. 1.8063 (10), 2.877 (9), 2.684 (8), 4.36 (5), 3.612 (5), 2.365 (5), 2.620 (4) Chemistry: (1) (2) (3) (1) (2) (3) SiO2 26.36 26.7 26.7 CaO 5.67 2.4 2.8 FeO trace 0.3 0.3 Na2O 0.39 MnO 60.63 62.8 64.7 K2O 0.24 ZnO 3.87 0.0 0.0 H2O 2.64 [2.3] [2.8] MgO 0.21 5.5 2.7 Total 100.01 [100.0] [100.0] (1) Franklin, New Jersey, USA; composite of two analyses, corresponding to (Mn5:89Ca0:70Zn0:32 Na0:04Mg0:03K0:01)§=6:99(Si1:01O4)3(OH)2: (2) Kombat mine, Namibia; by electron microprobe, H2O by di®erence; corresponding to (Mn5:98Mg0:92Ca0:29Fe0:02)§=7:21(SiO4)3(OH)1:72: (3) Valsesia-Valtournanche area, Italy; by electron microprobe, H2O by di®erence; corresponding to (Mn6:16Mg0:45Ca0:34Fe0:03)§=6:98(SiO4)3(OH)2:10: Mineral Group: Leucophoenicite group. -

TEPHROITE from FRANKLIN, NEW JERSEY* Connbrrus S. Hunrsur
THE AMERICAN MINERALOGIST, VOL 46, MAY_JUNE, 1961 TEPHROITE FROM FRANKLIN, NEW JERSEY* ConNBrrus S. Hunrsur, Jn., Departmentof Mineralogy, Harvard, Uniaersity. Assrnlcr A study of tephroite specimens from Franklin and Sterling Hill, New Jersey showed in all of them the presence of thin sheets of willemite believed to be a product of exsolution. .fhese sheets are oriented parallel to the {100} and [010] planes of tephroite with the o and r axes of tephroite and willemite parallel. It is believed that Iittle zinc remains in the tephroite structure and that much of it reported in chemical analyses has been con- tributed by intergrown u'illemite. This conclusion is supported by experiments syn- thesizing tephroite. The indices of refraction and d spacing of {130} vary as would be expected with changes in amounts of MgO, FeO and CaO. INrnooucrroN 'fephroite, Mn2SiO4,a member of the olivine group, was describedas a new mineral from SterlingHill by Breithaupt in 1823.A chemicalanal- ysis of the original material was published by Brush (1864) together with severaladditional chemical analysesof tephroite made by others. These analysesreport ZnO in varying amounts which Brush attributed to invariably associatedzincite. Palache (1937) did not agree with Brush and stated " . that the molecularratios in someanalyses more nearly satisfy the orthosilicateformula when zinc is regardedas essen- tially a part of the mineral rather than as a constituent of mechanical inclusions." The present study was undertaken for the purpose of in- vestigatingthe variations in the propertiesof tephroite with changesin chemical composition, particularly the effect of zinc. Relationships were not expectedto be simplefor analysesshow, in addition to ZnO, variable amounts of MgO, FeO, and CaO. -
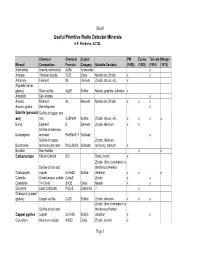
Useful Primitive Radio Detector Minerals H.P
Sheet1 Useful Primitive Radio Detector Minerals H.P. Friedichs, AC7ZL Chemical Chemical Crystal PW Eccles Toricata Morgan Mineral Composition Formula Category Suitable Contacts (1925) (1928) (1910) (1913) Allemontite Arsenic antimonide AsSb Antimonide x Anatase Titanium dioxide TiO2 Oxide Metals and Zincite x x Antimony Element Sb Element Zincite, silicon, etc. x Argentite (silver glance) Silver sulfide Ag2S Sulfide Metals, graphite, tellurium x Arkansite See Anatase x Arsenic Element As Element Metals and Zincite x x x Arsenic pyrites See Mispickel x Bornite (peacock Sulfide of copper and ore) iron Cu5FeS4 Sulfide Zincite, silicon, etc. x x x x Boron Element B Element Zincite, tellurium x x Sulfide of antimony Boulangerite and lead Pb5Sb4S11 Sulfosalt x Sulfide of copper, Zincite, tellurium, Bourmonite antimony and lead PbCuSbS3 Sulfosalt antimony, bismuth x Brookite See Anatase x x Carborundum Silicon Carbide SiC Steel, zincite x Zincite (this combination is Sulfide of iron and the famous Perikon Chalcopyrite copper CuFeS2 Sulfide detector) x x x Cobaltite Cobalt arsenic sulfide CoAsS Zincite x x Cassiterite Tin Oxide SnO2 Oxide Metals x x Cerussite Lead Carbonate PbCo3 Carbonate ?x Chalcocite (copper glance) Copper sulfide Cu2S Sulfide Zincite, tellurium x x x Zincite (this combination is Sulfide of iron and the famous Perikon Copper pyrites copper CuFeS2 Sulfide detector) x x Corundum Aluminum oxidde Al2O3 Oxide Zincite, bornite x Page 1 Sheet1 Covellite Copper sulfide CuS Sulfide Zincite, etc x x Cuprite (Cuprous oxide) Copper oxide -

By Michael Fleischer and Constance M. Schafer Open-File Report 81
U.S. DEPARTMENT OF THE INTERIOR GEOLOGICAL SURVEY THE FORD-FLEISCHER FILE OF MINERALOGICAL REFERENCES, 1978-1980 INCLUSIVE by Michael Fleischer and Constance M. Schafer Open-File Report 81-1174 This report is preliminary and has not been reviewed for conformity with U.S. Geological Survey editorial standards 1981 The Ford-Fleischer File of Mineralogical References 1978-1980 Inclusive by Michael Fleischer and Constance M. Schafer In 1916, Prof. W.E. Ford of Yale University, having just published the third Appendix to Dana's System of Mineralogy, 6th Edition, began to plan for the 7th Edition. He decided to create a file, with a separate folder for each mineral (or for each mineral group) into which he would place a citation to any paper that seemed to contain data that should be considered in the revision of the 6th Edition. He maintained the file in duplicate, with one copy going to Harvard University, when it was agreed in the early 1930's that Palache, Berman, and Fronde! there would have the main burden of the revision. A number of assistants were hired for the project, including C.W. Wolfe and M.A. Peacock to gather crystallographic data at Harvard, and Michael Fleischer to collect and evaluate chemical data at Yale. After Prof. Ford's death in March 1939, the second set of his files came to the U.S. Geological Survey and the literature has been covered since then by Michael Fleischer. Copies are now at the U.S. Geological Survey at Reston, Va., Denver, Colo., and Menlo Park, Cal., and at the U.S. -

Cambridge University Press 978-1-107-10626-0 — Minerals 2Nd Edition Index More Information
Cambridge University Press 978-1-107-10626-0 — Minerals 2nd Edition Index More Information Index Bold entries are mineral names. Page numbers in bold refer to minerals with detailed descriptions. Page numbers in italics refer to pictures. Abbe refractometer, 170, 191 American Mineralogist Crystal Structure Database, 143 aberrations in lenses, 172 amethyst, 50, 308, Plate 2c absorption, 217 amosite, 529 absorption of light, 186 optical micrograph, 532 absorption spectra, supernovae, 537 TEM image, 532 abundance of elements, 16 amphibole, 445 acetic acid, structure, 474 extinction angle, 212 acetone, structure, 474 minerals and composition, 439 acid mine drainage, 533 optical orientation, 211 actinolite, 449, 529 optical properties, 209 acute bisectrix, 199 quadrilateral, 444 adularia, 309 structure, 438 from Alps, Plate 21a amphibolite facies, 415 African Copper Belt, 374 analcime, 469 agate, 308 from Italy, SEM image, 465 aggregate, 518 analyzer, 173, 176 aggregation, 127 anatase, 392 of crystals, 127 from Swiss Alps, Plate 28d Agricola, 5, 481 structure and symmetry, 104 Airy’s spiral, 202 andalusite, 408 Al2SiO5, phase diagram, 276 optical orientation, 214 alabandite, 539 optical properties, 215 albite, 301, 310 porphyroblast, Plate 5c from New Mexico, Plate 21d andesine, 301 Albite twin law, 112, 311 anglesite, 355 Algoma-type iron deposits, 491 anhedral shape, 49 alite, 519 anhydrite, 355 alkali feldspars, 301, 309 animal nutrition, zeolites, 471 optical indicatrix, 205 aniom, 19 phase diagram, 306, 314 anisotropy, 149 alkali–silica