DOCSLIB.ORG

Resolving the Complexity of Some Fundamental Problems in Computational Social Choice

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Resolving the Complexity of Some Fundamental Problems in Computational Social Choice Resolving the Complexity of Some Fundamental Problems in Computational Social Choice A THESIS SUBMITTED FOR THE DEGREE OF Doctor of Philosophy IN THE Faculty of Engineering BY Palash Dey Computer Science and Automation Indian Institute of Science Bangalore { 560 012 (INDIA) August 2016 c Palash Dey August 2016 All rights reserved DEDICATED TO My teachers Acknowledgements I am grateful to my Ph.D. advisors Prof. Y. Narahari and Prof. Arnab Bhattacharyya for providing me a golden opportunity to work with them. I thank them for the all encompassing support they ushered upon me throughout my Ph.D. I convey my special thanks to Prof. Y. Narahari for all his academic and nonacademic supports which made my Ph.D. life very easy and enjoyable. I have throughly enjoyed working with Prof. Arnab Bhattacharyya. I convey my very special thanks to Prof. Neeldhara Misra for many excellent and successful research collaborations, useful discussions, and playing an all encompassing super-active role in my Ph.D. life. Prof. Neeldhara Misra was always my constant source of inspiration and she guided me throughout my Ph.D. as a supervisor, advisor, friend, and elder sister. I am indebted to Prof. Dilip P. Patil for teaching me how the practice of writing statements rigorously and precisely in mathematics automatically clarifies many doubts. I am extremely grateful to have a teacher like him at the very early stage of my stay in IISc who not only significantly improved my mathematical thinking process but also acted like a friend, philosopher, and guide throughout my stay in IISc. I throughly enjoyed all the courses that he taught during my stay in IISc and learned a lot from those courses. Specially his courses on linear algebra, Galois theory, commutative algebra have immensely influenced my thinking process. I thank Prof. Sunil Chandran for teaching me the art of proving results in graph theory in particular and theoretical computer science in general. I am grateful to Dr. Deeparnab Chakrabarty and Prof. Arnab Bhattacharyya for teaching me approximation algorithms and randomized algorithms, Prof. Manjunath Krishnapur for teaching me probability theory and martingales, Prof. Chandan Saha for teaching me complexity theory and algebraic geometry, Prof. Y. Narahari for teaching me game theory. I thank all the faculty members of Department of Computer Science and Automation (CSA) for all of their supports. I convey my special thank to all the staffs of CSA specially Ms. Suguna, Ms. Meenakshi, Ms. Kushael for their helping hands. I thank Prof. Ashish Goel for giving me an excellent opportunity to work with i Acknowledgements him and for hosting me in Stanford University for three months. I thank Dr. David Woodruff for collaborating with me on important problems. I feel myself extremely lucky to get such a wonderful and friendly lab members in the Game Theory lab. I want to thank all the members of the Game Theory lab with special mention to Dr. Rohith D. Vallam, Satyanath Bhat, Ganesh Ghalme, Shweta Jain, Swapnil Dhamal, Divya Padmanabhan, Dr. Pankaj Dayama, Praful Chandra, Shourya Roy, Tirumala Nathan, Debmalya Mandal, Arupratan Ray, and Arpita Biswas. I want to thank Dr. Minati De, Abhiruk Lahiri, Achintya Kundu, Aniket Basu Roy, Prabhu Chandran, Prasenjit Karmakar, R Kabaleeshwaran, Rohit Vaish, Sayantan Mukherjee, Srinivas Karthik, Suprovat Ghoshal, Vineet Nair for all the important discussions. I greatly acknowledge support from Ratul Ray and Uddipta Maity during my internship in Stanford University. I thank Google India for providing me fellowship during second and third years of my Ph.D. I acknowledge financial support from Ministry of Human Resource Development (MHRD) in India during my first year of Ph.D. Last but not the least, I express my gratitude to my parents, brother, wife, and all my friends for their love, blessing, encouragement, and support. ii Abstract In many real world situations, especially involving multiagent systems and artificial intel- ligence, participating agents often need to agree upon a common alternative even if they have differing preferences over the available alternatives. Voting is one of the tools of choice in these situations. Common and classic applications of voting in modern applications in- clude collaborative filtering and recommender systems, metasearch engines, coordination and planning among multiple automated agents etc. Agents in these applications usually have computational power at their disposal. This makes the study of computational aspects of voting crucial. This thesis is devoted to a study of computational complexity of several fundamental algorithmic and complexity-theoretic problems arising in the context of voting theory. The typical setting for our work is an “election”; an election consists of a set of voters or agents, a set of alternatives, and a voting rule. The vote of any agent can be thought of as a ranking (more precisely, a complete order) of the set of alternatives. A voting profile comprises a collection of votes of all the agents. Finally, a voting rule is a mapping that takes as input a voting profile and outputs an alternative, which is called the “winner” or “outcome” of the election. Our contributions in this thesis can be categorized into three parts and are described below. Part I: Preference Elicitation. In the first part of the thesis, we study the problem of elicit- ing the preferences of a set of voters by asking a small number of comparison queries (such as who a voter prefers between two given alternatives) for various interesting domains of preferences. We commence with considering the domain of single peaked preferences on trees in Chap- ter3. This domain is a significant generalization of the classical well studied domain of sin- gle peaked preferences. The domain of single peaked preferences and its generalizations are iii Abstract hugely popular among political and social scientists. We show tight dependencies between query complexity of preference elicitation and various parameters of the single peaked tree, for example, number of leaves, diameter, path width, maximum degree of a node etc. We next consider preference elicitation for the domain of single crossing preference pro- files in Chapter4. This domain has also been studied extensively by political scientists, social choice theorists, and computer scientists. We establish that the query complexity of pref- erence elicitation in this domain crucially depends on how the votes are accessed and on whether or not any single crossing ordering is a priori known. Part II: Winner Determination. In the second part of the thesis, we undertake a study of the computational complexity of several important problems related to determining winner of an election. We begin with a study of the following problem: Given an election, predict the winner of the election under some fixed voting rule by sampling as few votes as possible. We establish optimal or almost optimal bounds on the number of votes that one needs to sample for many commonly used voting rules when the margin of victory is at least "n (n is the number of voters and " is a parameter). We next study efficient sampling based algorithms for estimating the margin of victory of a given election for many common voting rules. The margin of victory of an election is a useful measure that captures the robustness of an election outcome. The above two works are presented in Chapter5. In Chapter6, we design an optimal algorithm for determining the plurality winner of an election when the votes are arriving one-by-one in a streaming fashion. This resolves an intriguing question on finding heavy hitters in a stream of items, that has remained open for more than 35 years in the data stream literature. We also provide near optimal algorithms for determining the winner of a stream of votes for other popular voting rules, for example, veto, Borda, maximin etc. Voters’ preferences are often partial orders instead of complete orders. This is known as the incomplete information setting in computational social choice theory. In an incomplete information setting, an extension of the winner determination problem which has been stud- ied extensively is the problem of determining possible winners. We study the kernelization complexity (under the complexity-theoretic framework of parameterized complexity) of the possible winner problem in Chapter7. We show that there do not exist kernels of size that is polynomial in the number of alternatives for this problem for commonly used voting rules iv Abstract under a plausible complexity theoretic assumption. However, we also show that the problem of coalitional manipulation which is an important special case of the possible winner prob- lem admits a kernel whose size is polynomially bounded in the number of alternatives for common voting rules. Part III: Election Control. In the final part of the thesis, we study the computational com- plexity of various interesting aspects of strategic behavior in voting. First, we consider the impact of partial information in the context of strategic manipu- lation in Chapter8. We show that lack of complete information makes the computational problem of manipulation intractable for many commonly used voting rules. In Chapter9, we initiate the study of the computational problem of detecting possible instances of election manipulation. We show that detecting manipulation may be computa- tionally easy under certain scenarios even when manipulation is intractable. The computational problem of bribery is an extensively studied problem in computational social choice theory. We study computational complexity of bribery when the briber is “fru- gal” in nature. We show for many common voting rules that the bribery problem remains intractable even when the briber’s behavior is restricted to be frugal, thereby strengthening the intractability results from the literature. This forms the subject of Chapter 10. v Publications based on this Thesis 1. Palash Dey, Neeldhara Misra, and Yadati Narahari. “Kernelization Complexity of Possible Winner and Coalitional Manipulation Problems in Voting”.
Load more

Recommended publications
  • Influences in Voting and Growing Networks
    UC Berkeley UC Berkeley Electronic Theses and Dissertations Title Influences in Voting and Growing Networks Permalink https://escholarship.org/uc/item/0fk1x7zx Author Racz, Miklos Zoltan Publication Date 2015 Peer reviewed|Thesis/dissertation eScholarship.org Powered by the California Digital Library University of California Influences in Voting and Growing Networks by Mikl´osZolt´anR´acz A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Statistics in the Graduate Division of the University of California, Berkeley Committee in charge: Professor Elchanan Mossel, Chair Professor James W. Pitman Professor Allan M. Sly Professor David S. Ahn Spring 2015 Influences in Voting and Growing Networks Copyright 2015 by Mikl´osZolt´anR´acz 1 Abstract Influences in Voting and Growing Networks by Mikl´osZolt´anR´acz Doctor of Philosophy in Statistics University of California, Berkeley Professor Elchanan Mossel, Chair This thesis studies problems in applied probability using combinatorial techniques. The first part of the thesis focuses on voting, and studies the average-case behavior of voting systems with respect to manipulation of their outcome by voters. Many results in the field of voting are negative; in particular, Gibbard and Satterthwaite showed that no reasonable voting system can be strategyproof (a.k.a. nonmanipulable). We prove a quantitative version of this result, showing that the probability of manipulation is nonnegligible, unless the voting system is close to being a dictatorship. We also study manipulation by a coalition of voters, and show that the transition from being powerless to having absolute power is smooth. These results suggest that manipulation is easy on average for reasonable voting systems, and thus computational complexity cannot hide manipulations completely.
    [Show full text]
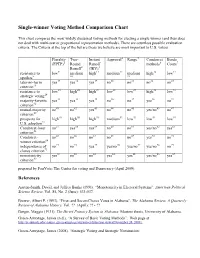
  • Single-Winner Voting Method Comparison Chart
    Single-winner Voting Method Comparison Chart This chart compares the most widely discussed voting methods for electing a single winner (and thus does not deal with multi-seat or proportional representation methods). There are countless possible evaluation criteria. The Criteria at the top of the list are those we believe are most important to U.S. voters. Plurality Two- Instant Approval4 Range5 Condorcet Borda (FPTP)1 Round Runoff methods6 Count7 Runoff2 (IRV)3 resistance to low9 medium high11 medium12 medium high14 low15 spoilers8 10 13 later-no-harm yes17 yes18 yes19 no20 no21 no22 no23 criterion16 resistance to low25 high26 high27 low28 low29 high30 low31 strategic voting24 majority-favorite yes33 yes34 yes35 no36 no37 yes38 no39 criterion32 mutual-majority no41 no42 yes43 no44 no45 yes/no 46 no47 criterion40 prospects for high49 high50 high51 medium52 low53 low54 low55 U.S. adoption48 Condorcet-loser no57 yes58 yes59 no60 no61 yes/no 62 yes63 criterion56 Condorcet- no65 no66 no67 no68 no69 yes70 no71 winner criterion64 independence of no73 no74 yes75 yes/no 76 yes/no 77 yes/no 78 no79 clones criterion72 81 82 83 84 85 86 87 monotonicity yes no no yes yes yes/no yes criterion80 prepared by FairVote: The Center for voting and Democracy (April 2009). References Austen-Smith, David, and Jeffrey Banks (1991). “Monotonicity in Electoral Systems”. American Political Science Review, Vol. 85, No. 2 (June): 531-537. Brewer, Albert P. (1993). “First- and Secon-Choice Votes in Alabama”. The Alabama Review, A Quarterly Review of Alabama History, Vol. ?? (April): ?? - ?? Burgin, Maggie (1931). The Direct Primary System in Alabama.
    [Show full text]
  • Cesifo Working Paper No. 9141
    A Service of Leibniz-Informationszentrum econstor Wirtschaft Leibniz Information Centre Make Your Publications Visible. zbw for Economics Pakhnin, Mikhail Working Paper Collective Choice with Heterogeneous Time Preferences CESifo Working Paper, No. 9141 Provided in Cooperation with: Ifo Institute – Leibniz Institute for Economic Research at the University of Munich Suggested Citation: Pakhnin, Mikhail (2021) : Collective Choice with Heterogeneous Time Preferences, CESifo Working Paper, No. 9141, Center for Economic Studies and Ifo Institute (CESifo), Munich This Version is available at: http://hdl.handle.net/10419/236683 Standard-Nutzungsbedingungen: Terms of use: Die Dokumente auf EconStor dürfen zu eigenen wissenschaftlichen Documents in EconStor may be saved and copied for your Zwecken und zum Privatgebrauch gespeichert und kopiert werden. personal and scholarly purposes. Sie dürfen die Dokumente nicht für öffentliche oder kommerzielle You are not to copy documents for public or commercial Zwecke vervielfältigen, öffentlich ausstellen, öffentlich zugänglich purposes, to exhibit the documents publicly, to make them machen, vertreiben oder anderweitig nutzen. publicly available on the internet, or to distribute or otherwise use the documents in public. Sofern die Verfasser die Dokumente unter Open-Content-Lizenzen (insbesondere CC-Lizenzen) zur Verfügung gestellt haben sollten, If the documents have been made available under an Open gelten abweichend von diesen Nutzungsbedingungen die in der dort Content Licence (especially Creative Commons Licences), you genannten Lizenz gewährten Nutzungsrechte. may exercise further usage rights as specified in the indicated licence. www.econstor.eu 9141 2021 June 2021 Collective Choice with Hetero- geneous Time Preferences Mikhail Pakhnin Impressum: CESifo Working Papers ISSN 2364-1428 (electronic version) Publisher and distributor: Munich Society for the Promotion of Economic Research - CESifo GmbH The international platform of Ludwigs-Maximilians University’s Center for Economic Studies and the ifo Institute Poschingerstr.
    [Show full text]
  • Ranked-Choice Voting from a Partisan Perspective
    Ranked-Choice Voting From a Partisan Perspective Jack Santucci December 21, 2020 Revised December 22, 2020 Abstract Ranked-choice voting (RCV) has come to mean a range of electoral systems. Broadly, they can facilitate (a) majority winners in single-seat districts, (b) majority rule with minority representation in multi-seat districts, or (c) majority sweeps in multi-seat districts. Such systems can be combined with other rules that encourage/discourage slate voting. This paper describes five major versions used in U.S. public elections: Al- ternative Vote (AV), single transferable vote (STV), block-preferential voting (BPV), the bottoms-up system, and AV with numbered posts. It then considers each from the perspective of a `political operative.' Simple models of voting (one with two parties, another with three) draw attention to real-world strategic issues: effects on minority representation, importance of party cues, and reasons for the political operative to care about how voters rank choices. Unsurprisingly, different rules produce different outcomes with the same votes. Specific problems from the operative's perspective are: majority reversal, serving two masters, and undisciplined third-party voters (e.g., `pure' independents). Some of these stem from well-known phenomena, e.g., ballot exhaus- tion/ranking truncation and inter-coalition \vote leakage." The paper also alludes to vote-management tactics, i.e., rationing nominations and ensuring even distributions of first-choice votes. Illustrative examples come from American history and comparative politics. (209 words.) Keywords: Alternative Vote, ballot exhaustion, block-preferential voting, bottoms- up system, exhaustive-preferential system, instant runoff voting, ranked-choice voting, sequential ranked-choice voting, single transferable vote, strategic coordination (10 keywords).
    [Show full text]
  • Präferenzaggregation Durch Wählen: Algorithmik Und Komplexität
    Pr¨aferenzaggregationdurch W¨ahlen: Algorithmik und Komplexit¨at Folien zur Vorlesung Wintersemester 2017/2018 Dozent: Prof. Dr. J. Rothe J. Rothe (HHU D¨usseldorf) Pr¨aferenzaggregation durch W¨ahlen 1 / 57 Preliminary Remarks Websites Websites Vorlesungswebsite: http:==ccc:cs:uni-duesseldorf:de=~rothe=wahlen Anmeldung im LSF J. Rothe (HHU D¨usseldorf) Pr¨aferenzaggregation durch W¨ahlen 2 / 57 Preliminary Remarks Literature Literature J. Rothe (Herausgeber): Economics and Computation: An Introduction to Algorithmic Game Theory, Computational Social Choice, and Fair Division. Springer-Verlag, 2015 with a preface by Matt O. Jackson und Yoav Shoham (Stanford) Buchblock 155 x 235 mm Abstand 6 mm Springer Texts in Business and Economics Rothe Springer Texts in Business and Economics Jörg Rothe Editor Economics and Computation Ed. An Introduction to Algorithmic Game Theory, Computational Social Choice, and Fair Division J. Rothe D. Baumeister C. Lindner I. Rothe This textbook connects three vibrant areas at the interface between economics and computer science: algorithmic game theory, computational social choice, and fair divi- sion. It thus offers an interdisciplinary treatment of collective decision making from an economic and computational perspective. Part I introduces to algorithmic game theory, focusing on both noncooperative and cooperative game theory. Part II introduces to Jörg Rothe Einführung in computational social choice, focusing on both preference aggregation (voting) and judgment aggregation. Part III introduces to fair division, focusing on the division of Editor Computational Social Choice both a single divisible resource ("cake-cutting") and multiple indivisible and unshare- able resources ("multiagent resource allocation"). In all these parts, much weight is Individuelle Strategien und kollektive given to the algorithmic and complexity-theoretic aspects of problems arising in these areas, and the interconnections between the three parts are of central interest.
    [Show full text]
  • Group Decision Making with Partial Preferences
    Group Decision Making with Partial Preferences by Tyler Lu A thesis submitted in conformity with the requirements for the degree of Doctor of Philosophy Graduate Department of Computer Science University of Toronto c Copyright 2015 by Tyler Lu Abstract Group Decision Making with Partial Preferences Tyler Lu Doctor of Philosophy Graduate Department of Computer Science University of Toronto 2015 Group decision making is of fundamental importance in all aspects of a modern society. Many commonly studied decision procedures require that agents provide full preference information. This requirement imposes significant cognitive and time burdens on agents, increases communication overhead, and infringes agent privacy. As a result, specifying full preferences is one of the contributing factors for the limited real-world adoption of some commonly studied voting rules. In this dissertation, we introduce a framework consisting of new concepts, algorithms, and theoretical results to provide a sound foundation on which we can address these problems by being able to make group decisions with only partial preference information. In particular, we focus on single and multi-winner voting. We introduce minimax regret (MMR), a group decision-criterion for partial preferences, which quantifies the loss in social welfare of chosen alternative(s) compared to the unknown, but true winning alternative(s). We develop polynomial-time algorithms for the computation of MMR for a number of common of voting rules, and prove intractability results for other rules. We address preference elicitation, the second part of our framework, which concerns the extraction of only the relevant agent preferences that reduce MMR. We develop a few elicitation strategies, based on common ideas, for different voting rules and query types.
    [Show full text]
  • A Phase Transition in Arrow's Theorem
    A Phase Transition in Arrow's Theorem Frederic Koehler∗ Elchanan Mossely Abstract Arrow's Theorem concerns a fundamental problem in social choice theory: given the individual preferences of members of a group, how can they be aggregated to form rational group preferences? Arrow showed that in an election between three or more candidates, there are situations where any voting rule satisfying a small list of natural \fairness" axioms must produce an apparently irrational intransitive outcome. Fur- thermore, quantitative versions of Arrow's Theorem in the literature show that when voters choose rankings in an i.i.d. fashion, the outcome is intransitive with non-negligible probability. It is natural to ask if such a quantitative version of Arrow's Theorem holds for non-i.i.d. models. To answer this question, we study Arrow's Theorem under a natural non-i.i.d. model of voters inspired by canonical models in statistical physics; indeed, a version of this model was previously introduced by Raffaelli and Marsili in the physics literature. This model has a parameter, temperature, that prescribes the correlation between different voters. We show that the behavior of Arrow's Theorem in this model undergoes a striking phase transition: in the entire high temperature regime of the model, a Quantitative Arrow's Theorem holds showing that the probability of paradox for any voting rule satisfying the axioms is non-negligible; this is tight because the probability of paradox under pairwise majority goes to zero when approaching the critical temperature, and becomes exponentially small in the number of voters beyond it.
    [Show full text]
  • Voting with Rank Dependent Scoring Rules
    Voting with Rank Dependent Scoring Rules Judy Goldsmith, Jer´ omeˆ Lang, Nicholas Mattei, and Patrice Perny Abstract Positional scoring rules in voting compute the score of an alternative by summing the scores for the alternative induced by every vote. This summation principle ensures that all votes con- tribute equally to the score of an alternative. We relax this assumption and, instead, aggregate scores by taking into account the rank of a score in the ordered list of scores obtained from the votes. This defines a new family of voting rules, rank-dependent scoring rules (RDSRs), based on ordered weighted average (OWA) operators, which include all scoring rules, and many oth- ers, most of which of new. We study some properties of these rules, and show, empirically, that certain RDSRs are less manipulable than Borda voting, across a variety of statistical cultures and on real world data from skating competitions. 1 Introduction Voting rules aim at aggregating the ordinal preferences of a set of individuals in order to produce a commonly chosen alternative. Many voting rules are defined in the following way: given a vot- ing profile P, a collection of votes, where a vote is a linear ranking over alternatives, each vote contributes to the score of an alternative. The global score of the alternative is then computed by summing up all these contributed (“local”) scores, and finally, the alternative(s) with the highest score win(s). The most common subclass of these scoring rules is that of positional scoring rules: the local score of x with respect to vote v depends only on the rank of x in v, and the global score of x is the sum, over all votes, of its local scores.
    [Show full text]
  • Math 105 Workbook Exploring Mathematics
    Math 105 Workbook Exploring Mathematics Douglas R. Anderson, Professor Fall 2018: MWF 11:50-1:00, ISC 101 Acknowledgment First we would like to thank all of our former Math 105 students. Their successes, struggles, and suggestions have shaped how we teach this course in many important ways. We also want to thank our departmental colleagues and several Concordia math- ematics majors for many fruitful discussions and resources on the content of this course and the makeup of this workbook. Some of the topics, examples, and exercises in this workbook are drawn from other works. Most significantly, we thank Samantha Briggs, Ellen Kramer, and Dr. Jessie Lenarz for their work in Exploring Mathematics, as well as other Cobber mathemat- ics professors. We have also used: • Taxicab Geometry: An Adventure in Non-Euclidean Geometry by Eugene F. Krause, • Excursions in Modern Mathematics, Sixth Edition, by Peter Tannenbaum. • Introductory Graph Theory by Gary Chartrand, • The Heart of Mathematics: An invitation to effective thinking by Edward B. Burger and Michael Starbird, • Applied Finite Mathematics by Edmond C. Tomastik. Finally, we want to thank (in advance) you, our current students. Your suggestions for this course and this workbook are always encouraged, either in person or over e-mail. Both the course and workbook are works in progress that will continue to improve each semester with your help. Let's have a great semester this fall exploring mathematics together and fulfilling Concordia's math requirement in 2018. Skol Cobbs! i ii Contents 1 Taxicab Geometry 3 1.1 Taxicab Distance . .3 Homework . .8 1.2 Taxicab Circles .
    [Show full text]
  • The Expanding Approvals Rule: Improving Proportional Representation and Monotonicity 3
    Working Paper The Expanding Approvals Rule: Improving Proportional Representation and Monotonicity Haris Aziz · Barton E. Lee Abstract Proportional representation (PR) is often discussed in voting settings as a major desideratum. For the past century or so, it is common both in practice and in the academic literature to jump to single transferable vote (STV) as the solution for achieving PR. Some of the most prominent electoral reform movements around the globe are pushing for the adoption of STV. It has been termed a major open prob- lem to design a voting rule that satisfies the same PR properties as STV and better monotonicity properties. In this paper, we first present a taxonomy of proportional representation axioms for general weak order preferences, some of which generalise and strengthen previously introduced concepts. We then present a rule called Expand- ing Approvals Rule (EAR) that satisfies properties stronger than the central PR axiom satisfied by STV, can handle indifferences in a convenient and computationally effi- cient manner, and also satisfies better candidate monotonicity properties. In view of this, our proposed rule seems to be a compelling solution for achieving proportional representation in voting settings. Keywords committee selection · multiwinner voting · proportional representation · single transferable vote. JEL Classification: C70 · D61 · D71 1 Introduction Of all modes in which a national representation can possibly be constituted, this one [STV] affords the best security for the intellectual qualifications de- sirable in the representatives—John Stuart Mill (Considerations on Represen- tative Government, 1861). arXiv:1708.07580v2 [cs.GT] 4 Jun 2018 H. Aziz · B. E. Lee Data61, CSIRO and UNSW, Sydney 2052 , Australia Tel.: +61-2-8306 0490 Fax: +61-2-8306 0405 E-mail: [email protected], [email protected] 2 Haris Aziz, Barton E.
    [Show full text]
  • Problems with Group Decision Making There Are Two Ways of Evaluating Political Systems
    Problems with Group Decision Making There are two ways of evaluating political systems. 1. Consequentialist ethics evaluate actions, policies, or institutions in regard to the outcomes they produce. 2. Deontological ethics evaluate actions, policies, or institutions in light of the rights, duties, or obligations of the individuals involved. Many people like democracy because they believe it to be a fair way to make decisions. One commonsense notion of fairness is that group decisions should reflect the preferences of the majority of group members. Most people probably agree that a fair way to decide between two options is to choose the option that is preferred by the most people. At its heart, democracy is a system in which the majority rules. An actor is rational if she possesses a complete and transitive preference ordering over a set of outcomes. An actor has a complete preference ordering if she can compare each pair of elements (call them x and y) in a set of outcomes in one of the following ways - either the actor prefers x to y, y to x, or she is indifferent between them. An actor has a transitive preference ordering if for any x, y, and z in the set of outcomes, it is the case that if x is weakly preferred to y, and y is weakly preferred to z, then it must be the case that x is weakly preferred to z. Condorcet's paradox illustrates that a group composed of individuals with rational preferences does not necessarily have rational preferences as a collectivity. Individual rationality is not sufficient to ensure group rationality.
    [Show full text]
  • List of Paradoxes 1 List of Paradoxes
    List of paradoxes 1 List of paradoxes This is a list of paradoxes, grouped thematically. The grouping is approximate: Paradoxes may fit into more than one category. Because of varying definitions of the term paradox, some of the following are not considered to be paradoxes by everyone. This list collects only those instances that have been termed paradox by at least one source and which have their own article. Although considered paradoxes, some of these are based on fallacious reasoning, or incomplete/faulty analysis. Logic • Barbershop paradox: The supposition that if one of two simultaneous assumptions leads to a contradiction, the other assumption is also disproved leads to paradoxical consequences. • What the Tortoise Said to Achilles "Whatever Logic is good enough to tell me is worth writing down...," also known as Carroll's paradox, not to be confused with the physical paradox of the same name. • Crocodile Dilemma: If a crocodile steals a child and promises its return if the father can correctly guess what the crocodile will do, how should the crocodile respond in the case that the father guesses that the child will not be returned? • Catch-22 (logic): In need of something which can only be had by not being in need of it. • Drinker paradox: In any pub there is a customer such that, if he or she drinks, everybody in the pub drinks. • Paradox of entailment: Inconsistent premises always make an argument valid. • Horse paradox: All horses are the same color. • Lottery paradox: There is one winning ticket in a large lottery. It is reasonable to believe of a particular lottery ticket that it is not the winning ticket, since the probability that it is the winner is so very small, but it is not reasonable to believe that no lottery ticket will win.
    [Show full text]