DOCSLIB.ORG

Voting Systems: from Method to Algorithm

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Voting Systems: from Method to Algorithm Voting Systems: From Method to Algorithm A Thesis Presented to The Faculty of the Com puter Science Department California State University Channel Islands In (Partial) Fulfillment of the Requirements for the Degree M asters of Science in Com puter Science b y Christopher R . Devlin Advisor: Michael Soltys December 2019 © 2019 Christopher R. Devlin ALL RIGHTS RESERVED APPROVED FOR MS IN COMPUTER SCIENCE Advisor: Dr. Michael Soltys Date Name: Dr. Bahareh Abbasi Date Name: Dr. Vida Vakilian Date APPROVED FOR THE UNIVERITY Name Date Acknowledgements I’d like to thank my wife, Eden Byrne for her patience and support while I completed this Masters Degree. I’d also like to thank Dr. Michael Soltys for his guidance and mentorship. Additionally I’d like to thank the faculty and my fellow students at CSUCI who have given nothing but assistance and encouragement during my time here. Voting Systems: From Method to Algorithm Christopher R. Devlin December 18, 2019 Abstract Voting and choice aggregation are used widely not just in poli­ tics but in business decision making processes and other areas such as competitive bidding procurement. Stakeholders and others who rely on these systems require them to be fast, efficient, and, most impor­ tantly, fair. The focus of this thesis is to illustrate the complexities inherent in voting systems. The algorithms intrinsic in several voting systems are made explicit as a way to simplify choices among these systems. The systematic evaluation of the algorithms associated with choice aggregation will provide a groundwork for future research and the implementation of these tools across public and private spheres. Contents 1 Introduction 1 1.1 Contribution of this Thesis ............................................................ 11 2 Background 14 3 Algorithms for Voting Systems 22 3.1 Approval v otin g ................................................................................ 22 3.2 Baldwin Method ............................................................................ 24 3.3 Borda Count ................................................................................... 27 3.4 Bucklin m eth od ................................................................................ 29 3.5 C on d orcet......................................................................................... 30 3.6 Coombs R u l e ................................................................................... 32 3.7 Exhaustive B a llot............................................................................ 35 3.8 Instant Runoff Voting...................................................................... 37 3.9 K em eny-Young................................................................................ 40 3.10 Majority Judgement ...................................................................... 43 3.11 Nanson's Method ............................................................................ 45 3.12 Plurality............................................................................................ 49 3.13 Range Voting ................................................................................... 50 3.14 Tideman method ............................................................................ 52 3.15 Schulze Method ................................................................................ 56 3.16 Veto System ...................................................................................... 61 i 4 Conclusion and future work 62 4.1 Conclusion......................................................................................... 62 4.2 Future W ork...................................................................................... 66 Appendices 67 ii List of Figures 1 Approval Voting Algorithm ......................................................... 23 2 Approval Voting Example............................................................ 23 3 Baldwin Method Algorithm ......................................................... 25 4 Baldwin Method Example ............................................................ 26 5 Borda Count Algorithm ................................................................ 28 6 Borda Count E x a m p le ................................................................... 28 7 Bucklin Method Algorithm............................................................ 29 8 Bucklin Method Example ............................................................ 30 9 Condorcet A lgorithm ...................................................................... 31 10 Condorcet Exam ple......................................................................... 32 11 Coombs R u l e ................................................................................... 33 12 Coombs Example ............................................................................ 34 13 Exhaustive Ballot Algorithm......................................................... 35 14 Exhaustive Ballot Example ............................................................ 36 15 Instant Runoff Voting...................................................................... 38 16 Instant Runoff Voting E x a m p le ................................................... 39 17 Kemeny-Young Algorithm ............................................................ 41 18 Kemeny-Young E xam ple................................................................ 42 19 Kemeny-Young Ranking S c o r e s ................................................... 43 20 Majority Judgment A lgorithm...................................................... 44 21 Majority Judgment Exam ple......................................................... 45 iii 2 2 N a n s o n ’ s M e t h o d A l g o r i t h m ............................................................................................. 4 7 2 3 N a n s o n ’ s M e t h o d E x a m p l e .................................................................................................. 4 8 2 4 P l u r a l i t y A l g o r i t h m ...................................................................................................................... 4 9 2 5 P l u r a l i t y E x a m p l e ........................................................................................................................... 5 0 2 6 R a n g e V o t i n g A l g o r i t h m ....................................................................................................... 5 1 2 7 R a n g e V o t i n g E x a m p l e ............................................................................................................ 5 2 2 8 T i d e m a n M e t h o d A l g o r i t h m ............................................................................................. 5 4 2 9 T i d e m a n M e t h o d E x a m p l e .................................................................................................. 5 5 3 0 T i d e m a n G r a p h ................................................................................................................................ 5 6 3 1 S c h u l z e M e t h o d A l g o r i t h m : S t a g e 1 [ 2 6 ] ................................................................ 5 8 3 2 S c h u l z e M e t h o d A l g o r i t h m : S t a g e 2 [ 2 6 ] ................................................................ 5 9 3 3 S c h u l z e M e t h o d A l g o r i t h m : S t a g e 3 [ 2 6 ] ................................................................ 6 0 3 4 S c h u l z e M e t h o d E x a m p l e ....................................................................................................... 6 0 iv 1 Introduction This thesis will examine common voting systems and restate them as algo­ rithms for the purpose of clarity and transparency. The necessity of this stems from the ubiquitous presence of algorithms in general in modern life and in creating an understanding between the application of these algorithms and end users. The use of preference aggregation has applications beyond the well known political sphere and is increasingly used in artificial intelli­ gence and multiagent systems. In situations where a group of people needs to decide between several alternatives there will generally be disagreements on which alternatives are the most and least desirable. This will necessitate the aggregation of individual preferences into a preference that is most accept­ able the largest number of stakeholders. The importance of this rests on the idea that all voting stakeholders feel that their preferences were considered and dealt with fairly. The use of voting in terms of politics covers not only who will wield the powers of the state but also how they will be allowed to allocate the vast sums of money and other resources. It seems then only natural to expect, and this is born out by history, that some groups will seek to manipulate or control the outcome of elections. As a formal rule, manipulation, also called strategic voting, exists when a voter has the ability to unilaterally change their ballot to secure a desired outcome [1]. This rule also assumes that the voter in question has perfect knowledge of how all others have or 1 will vote and that this voter will mark their choices in an insincere manner to secure their own preferred result. Control, as an alternative, is the use of election procedures by those running the election to change the outcome without changing who individuals may choose to vote for. Often this control is used to decide who can vote or run for office in the first
Load more

Recommended publications
  • Influences in Voting and Growing Networks
    UC Berkeley UC Berkeley Electronic Theses and Dissertations Title Influences in Voting and Growing Networks Permalink https://escholarship.org/uc/item/0fk1x7zx Author Racz, Miklos Zoltan Publication Date 2015 Peer reviewed|Thesis/dissertation eScholarship.org Powered by the California Digital Library University of California Influences in Voting and Growing Networks by Mikl´osZolt´anR´acz A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Statistics in the Graduate Division of the University of California, Berkeley Committee in charge: Professor Elchanan Mossel, Chair Professor James W. Pitman Professor Allan M. Sly Professor David S. Ahn Spring 2015 Influences in Voting and Growing Networks Copyright 2015 by Mikl´osZolt´anR´acz 1 Abstract Influences in Voting and Growing Networks by Mikl´osZolt´anR´acz Doctor of Philosophy in Statistics University of California, Berkeley Professor Elchanan Mossel, Chair This thesis studies problems in applied probability using combinatorial techniques. The first part of the thesis focuses on voting, and studies the average-case behavior of voting systems with respect to manipulation of their outcome by voters. Many results in the field of voting are negative; in particular, Gibbard and Satterthwaite showed that no reasonable voting system can be strategyproof (a.k.a. nonmanipulable). We prove a quantitative version of this result, showing that the probability of manipulation is nonnegligible, unless the voting system is close to being a dictatorship. We also study manipulation by a coalition of voters, and show that the transition from being powerless to having absolute power is smooth. These results suggest that manipulation is easy on average for reasonable voting systems, and thus computational complexity cannot hide manipulations completely.
    [Show full text]
  • Are Condorcet and Minimax Voting Systems the Best?1
    1 Are Condorcet and Minimax Voting Systems the Best?1 Richard B. Darlington Cornell University Abstract For decades, the minimax voting system was well known to experts on voting systems, but was not widely considered to be one of the best systems. But in recent years, two important experts, Nicolaus Tideman and Andrew Myers, have both recognized minimax as one of the best systems. I agree with that. This paper presents my own reasons for preferring minimax. The paper explicitly discusses about 20 systems. Comments invited. [email protected] Copyright Richard B. Darlington May be distributed free for non-commercial purposes Keywords Voting system Condorcet Minimax 1. Many thanks to Nicolaus Tideman, Andrew Myers, Sharon Weinberg, Eduardo Marchena, my wife Betsy Darlington, and my daughter Lois Darlington, all of whom contributed many valuable suggestions. 2 Table of Contents 1. Introduction and summary 3 2. The variety of voting systems 4 3. Some electoral criteria violated by minimax’s competitors 6 Monotonicity 7 Strategic voting 7 Completeness 7 Simplicity 8 Ease of voting 8 Resistance to vote-splitting and spoiling 8 Straddling 8 Condorcet consistency (CC) 8 4. Dismissing eight criteria violated by minimax 9 4.1 The absolute loser, Condorcet loser, and preference inversion criteria 9 4.2 Three anti-manipulation criteria 10 4.3 SCC/IIA 11 4.4 Multiple districts 12 5. Simulation studies on voting systems 13 5.1. Why our computer simulations use spatial models of voter behavior 13 5.2 Four computer simulations 15 5.2.1 Features and purposes of the studies 15 5.2.2 Further description of the studies 16 5.2.3 Results and discussion 18 6.
    [Show full text]
  • Stable Voting
    Stable Voting Wesley H. Hollidayy and Eric Pacuitz y University of California, Berkeley ([email protected]) z University of Maryland ([email protected]) September 12, 2021 Abstract In this paper, we propose a new single-winner voting system using ranked ballots: Stable Voting. The motivating principle of Stable Voting is that if a candidate A would win without another candidate B in the election, and A beats B in a head-to-head majority comparison, then A should still win in the election with B included (unless there is another candidate A0 who has the same kind of claim to winning, in which case a tiebreaker may choose between A and A0). We call this principle Stability for Winners (with Tiebreaking). Stable Voting satisfies this principle while also having a remarkable ability to avoid tied outcomes in elections even with small numbers of voters. 1 Introduction Voting reform efforts in the United States have achieved significant recent successes in replacing Plurality Voting with Instant Runoff Voting (IRV) for major political elections, including the 2018 San Francisco Mayoral Election and the 2021 New York City Mayoral Election. It is striking, by contrast, that Condorcet voting methods are not currently used in any political elections.1 Condorcet methods use the same ranked ballots as IRV but replace the counting of first-place votes with head- to-head comparisons of candidates: do more voters prefer candidate A to candidate B or prefer B to A? If there is a candidate A who beats every other candidate in such a head-to-head majority comparison, this so-called Condorcet winner wins the election.
    [Show full text]
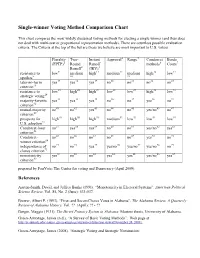
  • Single-Winner Voting Method Comparison Chart
    Single-winner Voting Method Comparison Chart This chart compares the most widely discussed voting methods for electing a single winner (and thus does not deal with multi-seat or proportional representation methods). There are countless possible evaluation criteria. The Criteria at the top of the list are those we believe are most important to U.S. voters. Plurality Two- Instant Approval4 Range5 Condorcet Borda (FPTP)1 Round Runoff methods6 Count7 Runoff2 (IRV)3 resistance to low9 medium high11 medium12 medium high14 low15 spoilers8 10 13 later-no-harm yes17 yes18 yes19 no20 no21 no22 no23 criterion16 resistance to low25 high26 high27 low28 low29 high30 low31 strategic voting24 majority-favorite yes33 yes34 yes35 no36 no37 yes38 no39 criterion32 mutual-majority no41 no42 yes43 no44 no45 yes/no 46 no47 criterion40 prospects for high49 high50 high51 medium52 low53 low54 low55 U.S. adoption48 Condorcet-loser no57 yes58 yes59 no60 no61 yes/no 62 yes63 criterion56 Condorcet- no65 no66 no67 no68 no69 yes70 no71 winner criterion64 independence of no73 no74 yes75 yes/no 76 yes/no 77 yes/no 78 no79 clones criterion72 81 82 83 84 85 86 87 monotonicity yes no no yes yes yes/no yes criterion80 prepared by FairVote: The Center for voting and Democracy (April 2009). References Austen-Smith, David, and Jeffrey Banks (1991). “Monotonicity in Electoral Systems”. American Political Science Review, Vol. 85, No. 2 (June): 531-537. Brewer, Albert P. (1993). “First- and Secon-Choice Votes in Alabama”. The Alabama Review, A Quarterly Review of Alabama History, Vol. ?? (April): ?? - ?? Burgin, Maggie (1931). The Direct Primary System in Alabama.
    [Show full text]
  • A Brief Introductory T T I L C T Ti L Tutorial on Computational Social Choice
    A Brief Introductory TtTutori ilal on Compu ttitationa l Social Choice Vincent Conitzer Outline • 1. Introduction to votinggy theory • 2. Hard-to-compute rules • 3. Using computational hardness to prevent manipulation and other undesirable behavior in elections • 4. Selected topics (time permitting) Introduction to voting theory Voting over alternatives voting rule > > (mechanism) determines winner based on votes > > • Can vote over other things too – Where to ggg,jp,o for dinner tonight, other joint plans, … Voting (rank aggregation) • Set of m candidates (aka. alternatives, outcomes) •n voters; each voter ranks all the candidates – E.g., for set of candidates {a, b, c, d}, one possible vote is b > a > d > c – Submitted ranking is called a vote • AvotingA voting rule takes as input a vector of votes (submitted by the voters), and as output produces either: – the winning candidate, or – an aggregate ranking of all candidates • Can vote over just about anything – pppolitical representatives, award nominees, where to go for dinner tonight, joint plans, allocations of tasks/resources, … – Also can consider other applications: e.g., aggregating search engines’ rankinggggs into a single ranking Example voting rules • Scoring rules are defined by a vector (a1, a2, …, am); being ranked ith in a vote gives the candidate ai points – Plurality is defined by (1, 0, 0, …, 0) (winner is candidate that is ranked first most often) – Veto (or anti-plurality) is defined by (1, 1, …, 1, 0) (winner is candidate that is ranked last the least often) – Borda is defined by (m-1, m-2, …, 0) • Plurality with (2-candidate) runoff: top two candidates in terms of plurality score proceed to runoff; whichever is ranked higher than the other by more voters, wins • Single Transferable Vote (STV, aka.
    [Show full text]
  • Governance in Decentralized Networks
    Governance in decentralized networks Risto Karjalainen* May 21, 2020 Abstract. Effective, legitimate and transparent governance is paramount for the long-term viability of decentralized networks. If the aim is to design such a governance model, it is useful to be aware of the history of decision making paradigms and the relevant previous research. Towards such ends, this paper is a survey of different governance models, the thinking behind such models, and new tools and structures which are made possible by decentralized blockchain technology. Governance mechanisms in the wider civil society are reviewed, including structures and processes in private and non-profit governance, open-source development, and self-managed organisations. The alternative ways to aggregate preferences, resolve conflicts, and manage resources in the decentralized space are explored, including the possibility of encoding governance rules as automatically executed computer programs where humans or other entities interact via a protocol. Keywords: Blockchain technology, decentralization, decentralized autonomous organizations, distributed ledger technology, governance, peer-to-peer networks, smart contracts. 1. Introduction This paper is a survey of governance models in decentralized networks, and specifically in networks which make use of blockchain technology. There are good reasons why governance in decentralized networks is a topic of considerable interest at present. Some of these reasons are ideological. We live in an era where detailed information about private individuals is being collected and traded, in many cases without the knowledge or consent of the individuals involved. Decentralized technology is seen as a tool which can help protect people against invasions of privacy. Decentralization can also be viewed as a reaction against the overreach by state and industry.
    [Show full text]
  • Majority Judgment: a New Voting Method
    Paradoxes Impossbilities Majority Judgment Theory Applications of MJ Logiciels JM Experimental Evidences Conclusion Majority Judgment: A New Voting Method Rida Laraki CNRS (Lamsade, Dauphine) and University of Liverpool Colloquium J. Morgenstern, INRIA, Sophia-Antipolis December 11, 2018 (Joint work with Michel Balinski) R. Laraki Majority Judgment: A New Voting Method Paradoxes Impossbilities Majority Judgment Theory ApplicationsMethods of MJ Logiciels of Voting JM Paradoxes Experimental in Theory Evidences Paradoxes Conclusion in Practice 1 Paradoxes Methods of Voting Paradoxes in Theory Paradoxes in Practice 2 Impossbilities May’s Axioms for Two Candidates Arrow’s Impossibility Theorem 3 Majority Judgment From Practice Small Jury Large Electorate 4 Theory Domination Paradox Possibility Manipulation 5 Applications of MJ Trump 2016 Gillets Jaunes Délé´gué CM1 6 Logiciels JM 7 Experimental Evidences 8 Conclusion R. Laraki Majority Judgment: A New Voting Method First-past-the-post: also called plurality voting, used in UK, US and Canada to elect members of house of representatives. A voter designate one candidate. The most designated wins. Two-past-the-post: used in France and several countries (Finland, Austria, Russia, Portugal, Ukraine, etc) to elect the president. A voter designates one candidate. If a candidate is designated by a majority, he is elected. Otherwise, there is a run-off between the two first candidates. Paradoxes Impossbilities Majority Judgment Theory ApplicationsMethods of MJ Logiciels of Voting JM Paradoxes Experimental in Theory Evidences Paradoxes Conclusion in Practice Voting methods most used in elections R. Laraki Majority Judgment: A New Voting Method A voter designate one candidate. The most designated wins. Two-past-the-post: used in France and several countries (Finland, Austria, Russia, Portugal, Ukraine, etc) to elect the president.
    [Show full text]
  • Strategic Behavior in Exhaustive Ballot Voting: What Can We Learn from the Fifa World Cup 2018 and 2022 Host Elections?
    Daniel Karabekyan STRATEGIC BEHAVIOR IN EXHAUSTIVE BALLOT VOTING: WHAT CAN WE LEARN FROM THE FIFA WORLD CUP 2018 AND 2022 HOST ELECTIONS? BASIC RESEARCH PROGRAM WORKING PAPERS SERIES: ECONOMICS WP BRP 130/EC/2016 This Working Paper is an output of a research project implemented at the National Research University Higher School of Economics (HSE). Any opinions or claims contained in this Working Paper do not necessarily reflect the views of HSE SERIES: ECONOMICS Daniel Karabekyan2 STRATEGIC BEHAVIOR IN EXHAUSTIVE BALLOT VOTING: WHAT CAN WE LEARN FROM THE FIFA WORLD CUP 2018 AND 2022 HOST ELECTIONS?*3 There are many allegations about whether FIFA world cup host countries were chosen honestly or not. We analyse the results of the FIFA Executive Committee voting and reconstruct the set of possible voting situations compatible with the results of each stage. In both elections, we identify strategic behaviour and then analyse the results for honest voting under all compatible voting situations. For the 2018 FIFA world cup election Russia is chosen for all profiles. For the 2022 elections the result depends on the preferences of the FIFA president Sepp Blatter who served as a tie-breaker. If Sepp Blatter prefers Qatar over South Korea and Japan, then Qatar would have been chosen for all profiles. Otherwise there are the possibility that South Korea or Japan would have been chosen as the 2022 host country. Another fact is that if we consider possible vote buying, then it is shown, that the bribery of at least 2 committee members would have been required to guarantee winning of Russia bid and at least 1 member for Qatar.
    [Show full text]
  • Generalized Scoring Rules: a Framework That Reconciles Borda and Condorcet
    Generalized Scoring Rules: A Framework That Reconciles Borda and Condorcet Lirong Xia Harvard University Generalized scoring rules [Xia and Conitzer 08] are a relatively new class of social choice mech- anisms. In this paper, we survey developments in generalized scoring rules, showing that they provide a fruitful framework to obtain general results, and also reconcile the Borda approach and Condorcet approach via a new social choice axiom. We comment on some high-level ideas behind GSRs and their connection to Machine Learning, and point out some ongoing work and future directions. Categories and Subject Descriptors: J.4 [Computer Applications]: Social and Behavioral Sci- ences|Economics; I.2.11 [Distributed Artificial Intelligence]: Multiagent Systems General Terms: Algorithms, Economics, Theory Additional Key Words and Phrases: Computational social choice, generalized scoring rules 1. INTRODUCTION Social choice theory focuses on developing principles and methods for representation and aggregation of individual ordinal preferences. Perhaps the most well-known application of social choice theory is political elections. Over centuries, many social choice mechanisms have been proposed and analyzed in the context of elections, where each agent (voter) uses a linear order over the alternatives (candidates) to represent her preferences (her vote). For historical reasons, we will use voting rules to denote social choice mechanisms, though we need to keep in mind that the application is not limited to political elections.1 Most existing voting rules fall into one of the following two categories.2 Positional scoring rules: Each alternative gets some points from each agent according to its position in the agent's vote. The alternative with the highest total points wins.
    [Show full text]
  • Electoral Systems Used Around the World
    Chapter 4 Electoral Systems Used around the World Siamak F. Shahandashti Newcastle University, UK CONTENTS 4.1 Introduction ::::::::::::::::::::::::::::::::::::::::::::::::::::::: 78 4.2 Some Solutions to Electing a Single Winner :::::::::::::::::::::::: 79 4.3 Some Solutions to Electing Multiple Winners ::::::::::::::::::::::: 82 4.4 Blending Systems Together :::::::::::::::::::::::::::::::::::::::: 87 4.5 Other Solutions :::::::::::::::::::::::::::::::::::::::::::::::::::: 88 4.6 Which Systems Are Good? ::::::::::::::::::::::::::::::::::::::::: 90 4.6.1 A Theorist’s Point of View ::::::::::::::::::::::::::::::::: 90 4.6.1.1 Majority Rules ::::::::::::::::::::::::::::::::: 90 4.6.1.2 Bad News Begins :::::::::::::::::::::::::::::: 91 4.6.1.3 Arrow’s Impossibility Theorem ::::::::::::::::: 93 4.6.1.4 Gibbard–Satterthwaite Impossibility Theorem ::: 94 4.6.1.5 Systems with Respect to Criteria :::::::::::::::: 95 4.6.2 A Practitioner’s Point of View ::::::::::::::::::::::::::::: 97 Acknowledgment ::::::::::::::::::::::::::::::::::::::::::::::::::::: 101 77 78 Real-World Electronic Voting: Design, Analysis and Deployment 4.1 Introduction An electoral system, or simply a voting method, defines the rules by which the choices or preferences of voters are collected, tallied, aggregated and collectively interpreted to obtain the results of an election [249, 489]. There are many electoral systems. A voter may be allowed to vote for one or multiple candidates, one or multiple predefined lists of candidates, or state their pref- erence among candidates or predefined lists of candidates. Accordingly, tallying may involve a simple count of the number of votes for each candidate or list, or a relatively more complex procedure of multiple rounds of counting and transferring ballots be- tween candidates or lists. Eventually, the outcome of the tallying and aggregation procedures is interpreted to determine which candidate wins which seat. Designing end-to-end verifiable e-voting schemes is challenging.
    [Show full text]
  • Lessons on Voting Reform from Britian's First Pr Elections
    WHAT WE ALREADY KNOW: LESSONS ON VOTING REFORM FROM BRITIAN'S FIRST PR ELECTIONS by Philip Cowley, University of Hull John Curtice, Strathclyde UniversityICREST Stephen Lochore, University of Hull Ben Seyd, The Constitution Unit April 2001 WHAT WE ALREADY KNOW: LESSONS ON VOTING REFORM FROM BRITIAN'S FIRST PR ELECTIONS Published by The Constitution Unit School of Public Policy UCL (University College London) 29/30 Tavistock Square London WClH 9QU Tel: 020 7679 4977 Fax: 020 7679 4978 Email: [email protected] Web: www.ucl.ac.uk/constitution-unit/ 0 The Constitution Unit. UCL 200 1 This report is sold subject ot the condition that is shall not, by way of trade or otherwise, be lent, hired out or otherwise circulated without the publisher's prior consent in any form of binding or cover other than that in which it is published and without a similar condition including this condition being imposed on the subsequent purchaser. First published April 2001 Contents Introduction ................................................................................................... 3 Executive Summary ..................................................................................4 Voters' attitudes to the new electoral systems ...........................................................4 Voters' behaviour under new electoral systems ......................................................... 4 Once elected .... The effect of PR on the Scottish Parliament in Practice ..................5 Voter Attitudes to the New Electoral Systems ............................................6
    [Show full text]
  • Majority Judgment Vs. Majority Rule ∗
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by University of Liverpool Repository Majority Judgment vs. Majority Rule ∗ Michel Balinski CNRS, CREST, Ecole´ Polytechnique, France, [email protected] and Rida Laraki* CNRS, University of Paris Dauphine-PSL, France, [email protected] and University of Liverpool, United Kingdom June 6, 2019 Abstract The validity of majority rule in an election with but two candidates|and so also of Condorcet consistency| is challenged. Axioms based on evaluating candidates|paralleling those of K. O. May characterizing ma- jority rule for two candidates based on comparing candidates|lead to another method, majority judgment, that is unique in agreeing with the majority rule on pairs of \polarized" candidates. It is a practical method that accommodates any number of candidates, avoids both the Condorcet and Arrow paradoxes, and best resists strategic manipulation. Key words: majority, measuring, ranking, electing, Condorcet consistency, domination paradox, tyranny of majority, intensity problem, majority-gauge, strategy-proofness, polarization. 1 Introduction Elections measure. Voters express themselves, a rule amalgamates them, the candidates' scores|measures of support|determine their order of finish, and the winner. Traditional methods ask voters to express themselves by comparing them: • ticking one candidate at most (majority rule, first-past-the-post) or several candidates (approval voting), candidates' total ticks ranking them; • rank-ordering the candidates (Borda rule, alternative vote or preferential voting, Llull's rule, Dasgupta- Maskin method, . ), differently derived numerical scores ranking them. However, no traditional method measures the support of one candidate.1 Instead, the theory of voting (or of social choice) elevates to a basic distinguishing axiom the faith that in an election between two candidates majority rule is the only proper rule.
    [Show full text]