DOCSLIB.ORG

Group Decision Making with Partial Preferences

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Group Decision Making with Partial Preferences Group Decision Making with Partial Preferences by Tyler Lu A thesis submitted in conformity with the requirements for the degree of Doctor of Philosophy Graduate Department of Computer Science University of Toronto c Copyright 2015 by Tyler Lu Abstract Group Decision Making with Partial Preferences Tyler Lu Doctor of Philosophy Graduate Department of Computer Science University of Toronto 2015 Group decision making is of fundamental importance in all aspects of a modern society. Many commonly studied decision procedures require that agents provide full preference information. This requirement imposes significant cognitive and time burdens on agents, increases communication overhead, and infringes agent privacy. As a result, specifying full preferences is one of the contributing factors for the limited real-world adoption of some commonly studied voting rules. In this dissertation, we introduce a framework consisting of new concepts, algorithms, and theoretical results to provide a sound foundation on which we can address these problems by being able to make group decisions with only partial preference information. In particular, we focus on single and multi-winner voting. We introduce minimax regret (MMR), a group decision-criterion for partial preferences, which quantifies the loss in social welfare of chosen alternative(s) compared to the unknown, but true winning alternative(s). We develop polynomial-time algorithms for the computation of MMR for a number of common of voting rules, and prove intractability results for other rules. We address preference elicitation, the second part of our framework, which concerns the extraction of only the relevant agent preferences that reduce MMR. We develop a few elicitation strategies, based on common ideas, for different voting rules and query types. While MMR can be applied in a distribution-free context, in many practical environ- ments decision makers have access to historical datasets of, and probabilistic knowledge of agent preferences. To leverage such information, we first address the problem of learn- ing probabilistic models of preferences from pairwise comparisons|the building block ii of many preference structures|for which previous techniques cannot handle. Then we extend our framework to a multi-round elicitation process that leverages probabilistic models to guide and analyze elicitation strategies. We empirically validate our framework and algorithms on real datasets. Experiments show our elicitation algorithms query only a fraction of full preferences to obtain alter- native(s) with small MMR. Experiments also show our learning algorithms can learn accurate mixture models of preference types, which we then use to guide the design of one-round top-k elicitation protocols. iii Dedication I dedicate this thesis to my family. iv Acknowledgements First and foremost, I would like to thank my advisor Craig Boutilier for assiduously guiding me during my PhD. Craig is a leading researcher in the AI community who is always enthusiastic about informing me of his new ideas, helping me push the envelope on my research, advising me throughout the research process, and engaging me in the broader research community. I would also like to thank members of my PhD committee: Alan Borodin, Martin Osborne and Rich Zemel. They were always available to talk to and provided advice and guidance throughout my PhD. They also sat in on my practice talks, listened carefully, took notes and had excellent questions, astute observations, and some great all around advice. I had the pleasure to work with, and to co-author papers with some of the best minds in all of computer science. They include Ariel Procaccia, Ioannis Caragiannis, Moshe Tenneholtz, Or Sheffet, Pingzhong Tang, Reshef Meir and Simi Haber. I am grateful to my colleagues in the research community who have provided plenty of feedback, ideas and support during my PhD. They include my co-authors, Jerome Lang, Lihi Dery, Lirong Xia, Meir Kalech, Tuomas Sandholm, Vincent Conitzer and many others whom I've had plenty of productive and enjoyable conversations with. I would also like to thank the AI faculty, including Geoff Hinton, Rich Zemel and Sheila McIlraith, who have taken an interest in my career, my research, and who have encouraged and cheered me on. It is this kind of collegial and caring environment that has boosted my self-confidence, ambitions and my drive to think big and do great things. I want to thank my fellow students who I can, and do, talk to about anything. There is no doubt that the people and culture that exists here is the reason the department is ranked so highly and one that has cultivated some of the leading researchers throughout the years. In fact, I would have to admit that sometimes my practice talks attracted a more intense and accomplished audience than the one in my actual talk at the actual conference. Luckily, they were all on my side. Being part of the Department of Computer Science during the past five years has been a great blessing. There have been some great research produced here, some great people flowing through here, and some great projects that have impacted society at large, sometimes through starting companies. There has never been a more exciting time to be here. v Contents 1 Introduction1 1.1 Overall Contributions.............................4 1.2 Organization of Dissertation.........................8 2 Overview of Social Choice 10 2.1 Preliminaries................................. 10 2.1.1 Preference Relations......................... 10 2.1.2 Partial Preferences.......................... 11 2.1.3 Distances over Preference Rankings................. 12 2.2 Single-Choice Problems............................ 13 2.3 Multi-Choice Problems............................ 19 2.4 Rank Aggregation............................... 22 2.5 Social Choice with Partial Preferences................... 25 2.5.1 Possible and Necessary Winners................... 26 2.5.2 Elicitation............................... 28 3 Robust Optimization and Elicitation for Single-Choice Problems 32 3.1 Robust Winner Determination........................ 33 3.1.1 Minimax Regret............................ 33 3.1.2 Relationship to Possible and Necessary Winners.......... 35 3.2 Computing Single-winner MMR....................... 36 3.2.1 Exploiting Pairwise Max Regret................... 37 3.2.2 Positional Scoring Rules....................... 37 3.2.3 Maximin Voting............................ 40 3.2.4 Bucklin Voting............................ 42 3.2.5 Egalitarian Voting.......................... 44 3.3 Preference Elicitation............................. 46 3.4 Empirical Evaluation............................. 50 vi 3.5 Related Work................................. 55 3.6 Conclusion................................... 56 4 Robust Optimization and Elicitation for Multiple-Choice Problems 58 4.1 Preliminaries................................. 58 4.2 Minimax Regret for Slate Optimization................... 59 4.2.1 Computing MMR-Optimal Slates.................. 60 4.2.2 A Greedy Algorithm for Robust Slate Optimization........ 64 4.3 Preference Elicitation............................. 69 4.4 Empirical Evaluation............................. 71 4.5 Conclusion................................... 75 5 Learning Rankings with Pairwise Preferences 77 5.1 Motivation................................... 78 5.2 Preliminaries................................. 80 5.2.1 Ordinal Preferences.......................... 80 5.2.2 Mallows Models and Sampling Procedures............. 82 5.2.3 A Mallows Mixture Model for Incomplete Preferences....... 90 5.3 Related Work................................. 91 5.4 Generalized Repeated Insertion Model................... 94 5.4.1 Sampling from Arbitrary Ranking Distributions.......... 94 5.4.2 Sampling from Mallows Posteriors.................. 96 5.4.3 Sampling Mallows Mixture Posterior................ 108 5.5 EM Learning Algorithm for Mallows Mixtures............... 108 5.5.1 Evaluating Log-Likelihood...................... 109 5.5.2 The EM Algorithm.......................... 111 5.5.3 Monte Carlo EM for Mallows Mixtures............... 112 5.5.4 Complexity of EM Steps....................... 116 5.6 Empirical Evaluation............................. 117 5.6.1 Sampling Quality........................... 118 5.6.2 Evaluating Log-Likelihood...................... 118 5.6.3 EM Mixture Learning........................ 119 5.6.4 Predicting Missing Pairwise Preferences............... 124 5.7 Applications to Non-Parametric Estimators................ 127 5.8 Conclusion................................... 130 vii 6 Elicitation with Probabilistic Preference Distributions 132 6.1 Motivation................................... 133 6.2 A Model of Multi-round Probabilistic Elicitation.............. 135 6.3 Probably Approximately Correct One-round Protocols.......... 138 6.4 Empirical Evaluation............................. 141 6.5 Conclusion................................... 149 7 Summary and Conclusions 150 7.1 Chapter Summary of Main Results..................... 151 7.2 Contributions................................. 153 7.3 Future Work.................................. 155 Bibliography 160 viii List of Tables 4.1 Avg. Greedy (slate) runtimes on Mallows data............... 74 5.1 Example of GRIM sampling on a conditional Mallows........... 96 5.2 Learned mixture model for sushi data (K = 6)............... 122 5.3 Learned mixture model for Movielens (K = 5)............... 125 5.4 Num. of missing pairwise comparisons at fixed distances......... 127
Load more

Recommended publications
  • Influences in Voting and Growing Networks
    UC Berkeley UC Berkeley Electronic Theses and Dissertations Title Influences in Voting and Growing Networks Permalink https://escholarship.org/uc/item/0fk1x7zx Author Racz, Miklos Zoltan Publication Date 2015 Peer reviewed|Thesis/dissertation eScholarship.org Powered by the California Digital Library University of California Influences in Voting and Growing Networks by Mikl´osZolt´anR´acz A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Statistics in the Graduate Division of the University of California, Berkeley Committee in charge: Professor Elchanan Mossel, Chair Professor James W. Pitman Professor Allan M. Sly Professor David S. Ahn Spring 2015 Influences in Voting and Growing Networks Copyright 2015 by Mikl´osZolt´anR´acz 1 Abstract Influences in Voting and Growing Networks by Mikl´osZolt´anR´acz Doctor of Philosophy in Statistics University of California, Berkeley Professor Elchanan Mossel, Chair This thesis studies problems in applied probability using combinatorial techniques. The first part of the thesis focuses on voting, and studies the average-case behavior of voting systems with respect to manipulation of their outcome by voters. Many results in the field of voting are negative; in particular, Gibbard and Satterthwaite showed that no reasonable voting system can be strategyproof (a.k.a. nonmanipulable). We prove a quantitative version of this result, showing that the probability of manipulation is nonnegligible, unless the voting system is close to being a dictatorship. We also study manipulation by a coalition of voters, and show that the transition from being powerless to having absolute power is smooth. These results suggest that manipulation is easy on average for reasonable voting systems, and thus computational complexity cannot hide manipulations completely.
    [Show full text]
  • Stable Voting
    Stable Voting Wesley H. Hollidayy and Eric Pacuitz y University of California, Berkeley ([email protected]) z University of Maryland ([email protected]) September 12, 2021 Abstract In this paper, we propose a new single-winner voting system using ranked ballots: Stable Voting. The motivating principle of Stable Voting is that if a candidate A would win without another candidate B in the election, and A beats B in a head-to-head majority comparison, then A should still win in the election with B included (unless there is another candidate A0 who has the same kind of claim to winning, in which case a tiebreaker may choose between A and A0). We call this principle Stability for Winners (with Tiebreaking). Stable Voting satisfies this principle while also having a remarkable ability to avoid tied outcomes in elections even with small numbers of voters. 1 Introduction Voting reform efforts in the United States have achieved significant recent successes in replacing Plurality Voting with Instant Runoff Voting (IRV) for major political elections, including the 2018 San Francisco Mayoral Election and the 2021 New York City Mayoral Election. It is striking, by contrast, that Condorcet voting methods are not currently used in any political elections.1 Condorcet methods use the same ranked ballots as IRV but replace the counting of first-place votes with head- to-head comparisons of candidates: do more voters prefer candidate A to candidate B or prefer B to A? If there is a candidate A who beats every other candidate in such a head-to-head majority comparison, this so-called Condorcet winner wins the election.
    [Show full text]
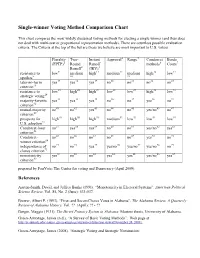
  • Single-Winner Voting Method Comparison Chart
    Single-winner Voting Method Comparison Chart This chart compares the most widely discussed voting methods for electing a single winner (and thus does not deal with multi-seat or proportional representation methods). There are countless possible evaluation criteria. The Criteria at the top of the list are those we believe are most important to U.S. voters. Plurality Two- Instant Approval4 Range5 Condorcet Borda (FPTP)1 Round Runoff methods6 Count7 Runoff2 (IRV)3 resistance to low9 medium high11 medium12 medium high14 low15 spoilers8 10 13 later-no-harm yes17 yes18 yes19 no20 no21 no22 no23 criterion16 resistance to low25 high26 high27 low28 low29 high30 low31 strategic voting24 majority-favorite yes33 yes34 yes35 no36 no37 yes38 no39 criterion32 mutual-majority no41 no42 yes43 no44 no45 yes/no 46 no47 criterion40 prospects for high49 high50 high51 medium52 low53 low54 low55 U.S. adoption48 Condorcet-loser no57 yes58 yes59 no60 no61 yes/no 62 yes63 criterion56 Condorcet- no65 no66 no67 no68 no69 yes70 no71 winner criterion64 independence of no73 no74 yes75 yes/no 76 yes/no 77 yes/no 78 no79 clones criterion72 81 82 83 84 85 86 87 monotonicity yes no no yes yes yes/no yes criterion80 prepared by FairVote: The Center for voting and Democracy (April 2009). References Austen-Smith, David, and Jeffrey Banks (1991). “Monotonicity in Electoral Systems”. American Political Science Review, Vol. 85, No. 2 (June): 531-537. Brewer, Albert P. (1993). “First- and Secon-Choice Votes in Alabama”. The Alabama Review, A Quarterly Review of Alabama History, Vol. ?? (April): ?? - ?? Burgin, Maggie (1931). The Direct Primary System in Alabama.
    [Show full text]
  • A Brief Introductory T T I L C T Ti L Tutorial on Computational Social Choice
    A Brief Introductory TtTutori ilal on Compu ttitationa l Social Choice Vincent Conitzer Outline • 1. Introduction to votinggy theory • 2. Hard-to-compute rules • 3. Using computational hardness to prevent manipulation and other undesirable behavior in elections • 4. Selected topics (time permitting) Introduction to voting theory Voting over alternatives voting rule > > (mechanism) determines winner based on votes > > • Can vote over other things too – Where to ggg,jp,o for dinner tonight, other joint plans, … Voting (rank aggregation) • Set of m candidates (aka. alternatives, outcomes) •n voters; each voter ranks all the candidates – E.g., for set of candidates {a, b, c, d}, one possible vote is b > a > d > c – Submitted ranking is called a vote • AvotingA voting rule takes as input a vector of votes (submitted by the voters), and as output produces either: – the winning candidate, or – an aggregate ranking of all candidates • Can vote over just about anything – pppolitical representatives, award nominees, where to go for dinner tonight, joint plans, allocations of tasks/resources, … – Also can consider other applications: e.g., aggregating search engines’ rankinggggs into a single ranking Example voting rules • Scoring rules are defined by a vector (a1, a2, …, am); being ranked ith in a vote gives the candidate ai points – Plurality is defined by (1, 0, 0, …, 0) (winner is candidate that is ranked first most often) – Veto (or anti-plurality) is defined by (1, 1, …, 1, 0) (winner is candidate that is ranked last the least often) – Borda is defined by (m-1, m-2, …, 0) • Plurality with (2-candidate) runoff: top two candidates in terms of plurality score proceed to runoff; whichever is ranked higher than the other by more voters, wins • Single Transferable Vote (STV, aka.
    [Show full text]
  • Generalized Scoring Rules: a Framework That Reconciles Borda and Condorcet
    Generalized Scoring Rules: A Framework That Reconciles Borda and Condorcet Lirong Xia Harvard University Generalized scoring rules [Xia and Conitzer 08] are a relatively new class of social choice mech- anisms. In this paper, we survey developments in generalized scoring rules, showing that they provide a fruitful framework to obtain general results, and also reconcile the Borda approach and Condorcet approach via a new social choice axiom. We comment on some high-level ideas behind GSRs and their connection to Machine Learning, and point out some ongoing work and future directions. Categories and Subject Descriptors: J.4 [Computer Applications]: Social and Behavioral Sci- ences|Economics; I.2.11 [Distributed Artificial Intelligence]: Multiagent Systems General Terms: Algorithms, Economics, Theory Additional Key Words and Phrases: Computational social choice, generalized scoring rules 1. INTRODUCTION Social choice theory focuses on developing principles and methods for representation and aggregation of individual ordinal preferences. Perhaps the most well-known application of social choice theory is political elections. Over centuries, many social choice mechanisms have been proposed and analyzed in the context of elections, where each agent (voter) uses a linear order over the alternatives (candidates) to represent her preferences (her vote). For historical reasons, we will use voting rules to denote social choice mechanisms, though we need to keep in mind that the application is not limited to political elections.1 Most existing voting rules fall into one of the following two categories.2 Positional scoring rules: Each alternative gets some points from each agent according to its position in the agent's vote. The alternative with the highest total points wins.
    [Show full text]
  • Approval-Based Elections and Distortion of Voting Rules
    Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence (IJCAI-19) Approval-Based Elections and Distortion of Voting Rules Grzegorz Pierczynski , Piotr Skowron University of Warsaw, Warsaw, Poland [email protected], [email protected] Abstract voters and the candidates are represented by points in a metric space M called the issue space. The optimal candidate is the We consider elections where both voters and can- one that minimizes the sum of the distances to all the voters. didates can be associated with points in a metric However, the election rules do not have access to the met- space and voters prefer candidates that are closer to ric space M itself but they only see the ranking-based profile those that are farther away. It is often assumed that induced by M: in this profile the voters rank the candidates the optimal candidate is the one that minimizes the by their distance to themselves, preferring the ones that are total distance to the voters. Yet, the voting rules of- closer to those that are farther. Since the rules do not have ten do not have access to the metric space M and full information about the metric space they cannot always only see preference rankings induced by M. Con- find optimal candidates. The distortion quantifies the worst- sequently, they often are incapable of selecting the case loss of the utility being effect of having only access to optimal candidate. The distortion of a voting rule rankings. Formally, the distortion of a voting rule is the max- measures the worst-case loss of the quality being imum, over all metric spaces, of the following ratio: the sum the result of having access only to preference rank- of the distances between the elected candidate and the vot- ings.
    [Show full text]
  • Ranked-Choice Voting from a Partisan Perspective
    Ranked-Choice Voting From a Partisan Perspective Jack Santucci December 21, 2020 Revised December 22, 2020 Abstract Ranked-choice voting (RCV) has come to mean a range of electoral systems. Broadly, they can facilitate (a) majority winners in single-seat districts, (b) majority rule with minority representation in multi-seat districts, or (c) majority sweeps in multi-seat districts. Such systems can be combined with other rules that encourage/discourage slate voting. This paper describes five major versions used in U.S. public elections: Al- ternative Vote (AV), single transferable vote (STV), block-preferential voting (BPV), the bottoms-up system, and AV with numbered posts. It then considers each from the perspective of a `political operative.' Simple models of voting (one with two parties, another with three) draw attention to real-world strategic issues: effects on minority representation, importance of party cues, and reasons for the political operative to care about how voters rank choices. Unsurprisingly, different rules produce different outcomes with the same votes. Specific problems from the operative's perspective are: majority reversal, serving two masters, and undisciplined third-party voters (e.g., `pure' independents). Some of these stem from well-known phenomena, e.g., ballot exhaus- tion/ranking truncation and inter-coalition \vote leakage." The paper also alludes to vote-management tactics, i.e., rationing nominations and ensuring even distributions of first-choice votes. Illustrative examples come from American history and comparative politics. (209 words.) Keywords: Alternative Vote, ballot exhaustion, block-preferential voting, bottoms- up system, exhaustive-preferential system, instant runoff voting, ranked-choice voting, sequential ranked-choice voting, single transferable vote, strategic coordination (10 keywords).
    [Show full text]
  • Präferenzaggregation Durch Wählen: Algorithmik Und Komplexität
    Pr¨aferenzaggregationdurch W¨ahlen: Algorithmik und Komplexit¨at Folien zur Vorlesung Wintersemester 2017/2018 Dozent: Prof. Dr. J. Rothe J. Rothe (HHU D¨usseldorf) Pr¨aferenzaggregation durch W¨ahlen 1 / 57 Preliminary Remarks Websites Websites Vorlesungswebsite: http:==ccc:cs:uni-duesseldorf:de=~rothe=wahlen Anmeldung im LSF J. Rothe (HHU D¨usseldorf) Pr¨aferenzaggregation durch W¨ahlen 2 / 57 Preliminary Remarks Literature Literature J. Rothe (Herausgeber): Economics and Computation: An Introduction to Algorithmic Game Theory, Computational Social Choice, and Fair Division. Springer-Verlag, 2015 with a preface by Matt O. Jackson und Yoav Shoham (Stanford) Buchblock 155 x 235 mm Abstand 6 mm Springer Texts in Business and Economics Rothe Springer Texts in Business and Economics Jörg Rothe Editor Economics and Computation Ed. An Introduction to Algorithmic Game Theory, Computational Social Choice, and Fair Division J. Rothe D. Baumeister C. Lindner I. Rothe This textbook connects three vibrant areas at the interface between economics and computer science: algorithmic game theory, computational social choice, and fair divi- sion. It thus offers an interdisciplinary treatment of collective decision making from an economic and computational perspective. Part I introduces to algorithmic game theory, focusing on both noncooperative and cooperative game theory. Part II introduces to Jörg Rothe Einführung in computational social choice, focusing on both preference aggregation (voting) and judgment aggregation. Part III introduces to fair division, focusing on the division of Editor Computational Social Choice both a single divisible resource ("cake-cutting") and multiple indivisible and unshare- able resources ("multiagent resource allocation"). In all these parts, much weight is Individuelle Strategien und kollektive given to the algorithmic and complexity-theoretic aspects of problems arising in these areas, and the interconnections between the three parts are of central interest.
    [Show full text]
  • Computational Perspectives on Democracy
    Computational Perspectives on Democracy Anson Kahng CMU-CS-21-126 August 2021 Computer Science Department School of Computer Science Carnegie Mellon University Pittsburgh, PA 15213 Thesis Committee: Ariel Procaccia (Chair) Chinmay Kulkarni Nihar Shah Vincent Conitzer (Duke University) David Pennock (Rutgers University) Submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy. Copyright c 2021 Anson Kahng This research was sponsored by the National Science Foundation under grant numbers IIS-1350598, CCF- 1525932, and IIS-1714140, the Department of Defense under grant number W911NF1320045, the Office of Naval Research under grant number N000141712428, and the JP Morgan Research grant. The views and conclusions contained in this document are those of the author and should not be interpreted as representing the official policies, either expressed or implied, of any sponsoring institution, the U.S. government or any other entity. Keywords: Computational Social Choice, Theoretical Computer Science, Artificial Intelligence For Grandpa and Harabeoji. iv Abstract Democracy is a natural approach to large-scale decision-making that allows people affected by a potential decision to provide input about the outcome. However, modern implementations of democracy are based on outdated infor- mation technology and must adapt to the changing technological landscape. This thesis explores the relationship between computer science and democracy, which is, crucially, a two-way street—just as principles from computer science can be used to analyze and design democratic paradigms, ideas from democracy can be used to solve hard problems in computer science. Question 1: What can computer science do for democracy? To explore this first question, we examine the theoretical foundations of three democratic paradigms: liquid democracy, participatory budgeting, and multiwinner elections.
    [Show full text]
  • Measuring Violations of Positive Involvement in Voting*
    Measuring Violations of Positive Involvement in Voting* Wesley H. Holliday Eric Pacuit University of California, Berkeley University of Maryland [email protected] [email protected] In the context of computational social choice, we study voting methods that assign a set of winners to each profile of voter preferences. A voting method satisfies the property of positive involvement (PI) if for any election in which a candidate x would be among the winners, adding another voter to the election who ranks x first does not cause x to lose. Surprisingly, a number of standard voting methods violate this natural property. In this paper, we investigate different ways of measuring the extent to which a voting method violates PI, using computer simulations. We consider the probability (under different probability models for preferences) of PI violations in randomly drawn profiles vs. profile- coalition pairs (involving coalitions of different sizes). We argue that in order to choose between a voting method that satisfies PI and one that does not, we should consider the probability of PI violation conditional on the voting methods choosing different winners. We should also relativize the probability of PI violation to what we call voter potency, the probability that a voter causes a candidate to lose. Although absolute frequencies of PI violations may be low, after this conditioning and relativization, we see that under certain voting methods that violate PI, much of a voter’s potency is turned against them—in particular, against their desire to see their favorite candidate elected. 1 Introduction Voting provides a mechanism for resolving conflicts between the preferences of multiple agents in order to arrive at a group choice.
    [Show full text]
  • Voting with Rank Dependent Scoring Rules
    Voting with Rank Dependent Scoring Rules Judy Goldsmith, Jer´ omeˆ Lang, Nicholas Mattei, and Patrice Perny Abstract Positional scoring rules in voting compute the score of an alternative by summing the scores for the alternative induced by every vote. This summation principle ensures that all votes con- tribute equally to the score of an alternative. We relax this assumption and, instead, aggregate scores by taking into account the rank of a score in the ordered list of scores obtained from the votes. This defines a new family of voting rules, rank-dependent scoring rules (RDSRs), based on ordered weighted average (OWA) operators, which include all scoring rules, and many oth- ers, most of which of new. We study some properties of these rules, and show, empirically, that certain RDSRs are less manipulable than Borda voting, across a variety of statistical cultures and on real world data from skating competitions. 1 Introduction Voting rules aim at aggregating the ordinal preferences of a set of individuals in order to produce a commonly chosen alternative. Many voting rules are defined in the following way: given a vot- ing profile P, a collection of votes, where a vote is a linear ranking over alternatives, each vote contributes to the score of an alternative. The global score of the alternative is then computed by summing up all these contributed (“local”) scores, and finally, the alternative(s) with the highest score win(s). The most common subclass of these scoring rules is that of positional scoring rules: the local score of x with respect to vote v depends only on the rank of x in v, and the global score of x is the sum, over all votes, of its local scores.
    [Show full text]
  • Math 105 Workbook Exploring Mathematics
    Math 105 Workbook Exploring Mathematics Douglas R. Anderson, Professor Fall 2018: MWF 11:50-1:00, ISC 101 Acknowledgment First we would like to thank all of our former Math 105 students. Their successes, struggles, and suggestions have shaped how we teach this course in many important ways. We also want to thank our departmental colleagues and several Concordia math- ematics majors for many fruitful discussions and resources on the content of this course and the makeup of this workbook. Some of the topics, examples, and exercises in this workbook are drawn from other works. Most significantly, we thank Samantha Briggs, Ellen Kramer, and Dr. Jessie Lenarz for their work in Exploring Mathematics, as well as other Cobber mathemat- ics professors. We have also used: • Taxicab Geometry: An Adventure in Non-Euclidean Geometry by Eugene F. Krause, • Excursions in Modern Mathematics, Sixth Edition, by Peter Tannenbaum. • Introductory Graph Theory by Gary Chartrand, • The Heart of Mathematics: An invitation to effective thinking by Edward B. Burger and Michael Starbird, • Applied Finite Mathematics by Edmond C. Tomastik. Finally, we want to thank (in advance) you, our current students. Your suggestions for this course and this workbook are always encouraged, either in person or over e-mail. Both the course and workbook are works in progress that will continue to improve each semester with your help. Let's have a great semester this fall exploring mathematics together and fulfilling Concordia's math requirement in 2018. Skol Cobbs! i ii Contents 1 Taxicab Geometry 3 1.1 Taxicab Distance . .3 Homework . .8 1.2 Taxicab Circles .
    [Show full text]