DOCSLIB.ORG

Computational Perspectives on Democracy

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Computational Perspectives on Democracy Computational Perspectives on Democracy Anson Kahng CMU-CS-21-126 August 2021 Computer Science Department School of Computer Science Carnegie Mellon University Pittsburgh, PA 15213 Thesis Committee: Ariel Procaccia (Chair) Chinmay Kulkarni Nihar Shah Vincent Conitzer (Duke University) David Pennock (Rutgers University) Submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy. Copyright c 2021 Anson Kahng This research was sponsored by the National Science Foundation under grant numbers IIS-1350598, CCF- 1525932, and IIS-1714140, the Department of Defense under grant number W911NF1320045, the Office of Naval Research under grant number N000141712428, and the JP Morgan Research grant. The views and conclusions contained in this document are those of the author and should not be interpreted as representing the official policies, either expressed or implied, of any sponsoring institution, the U.S. government or any other entity. Keywords: Computational Social Choice, Theoretical Computer Science, Artificial Intelligence For Grandpa and Harabeoji. iv Abstract Democracy is a natural approach to large-scale decision-making that allows people affected by a potential decision to provide input about the outcome. However, modern implementations of democracy are based on outdated infor- mation technology and must adapt to the changing technological landscape. This thesis explores the relationship between computer science and democracy, which is, crucially, a two-way street—just as principles from computer science can be used to analyze and design democratic paradigms, ideas from democracy can be used to solve hard problems in computer science. Question 1: What can computer science do for democracy? To explore this first question, we examine the theoretical foundations of three democratic paradigms: liquid democracy, participatory budgeting, and multiwinner elections. Each of these paradigms broadly redistributes power from the few to the many: For instance, liquid democracy allows people to choose delegates more flexibly and participatory budgeting enables citizens to directly influence government spending toward public projects. However, be- cause these paradigms are relatively new, their theoretical properties are rel- atively unexplored. We analyze each of these three settings from the point of view of computational social choice, which is a mathematical framework for collective decision-making. In particular, we focus on a combination of robust- ness, fairness, and efficiency with the end goal of providing actionable advice for future iterations of these paradigms. Question 2: What can democracy do for computer science? Toward this end, we explore two settings in which democratic principles can be used to augment approaches to making difficult decisions—in our case, automating ethical decision-making and hiring in online labor markets. Both of these problems are difficult in the sense that there is no universally agreed- upon function to optimize, making them a poor fit for traditional approaches in computer science. Instead, we try to emulate a world in which we can get input from people in order to arrive at a “societal” decision. In each of these settings, we first propose and analyze a theoretical approach that leads a single decision, and then, in collaboration with HCI researchers, run experiments in the real world to test the efficacy and practicability of our approaches in the real world. vi Acknowledgments First and foremost, I must thank Ariel Procaccia, my advisor, for being the best advisor anyone could hope for. You have taught me so much, not only technically, but also with respect to writing effective papers, giving better talks, mentoring junior students, and providing me with a sustainable example of healthy (and productive!) work-life balance. I will strive to learn from and emulate your unrivaled blend of brilliance, eloquence, and patience. Thank you for everything. To my thesis committee, Vince Conitzer, Chinmay Kulkarni, David Pen- nock, and Nihar Shah, thank you for your insightful comments and wonderful questions that have helped me structure and present my work. I truly appre- ciate all the comments and questions, even if I may not have all the answers yet! To the professors at Harvard that led me down the grad school path: David and Yiling. Thank you for opening my eyes to the wonders of Econ-CS (or CS- Econ here at CMU), for supervising my first attempt at independent research (David), and for your continued support and guidance over the years. To my collaborators: Gerdus Benadè, Allissa Chan, Rupert Freeman, Paul Gölz, Bernhard Haeupler, Ellis Hershkowitz, Gregory Kehne, Ji Tae Kim, Yas- mine Kotturi, Chinmay Kulkarni, David Kurokawa, Daniel Kusbit, Min Kyung Lee, Siheon Lee, Simon Mackenzie, Ritesh Noothigattu, David Pennock, Do- minik Peters, Ariel Procaccia, Alex Psomas, Daniel See, and Xinran Yuan. I truly enjoyed collaborating with each and every one of you, and thank you for bringing your expertise and hard work to the projects we worked on together. To my friends: Ellis, Alex, Greg, Roie, Mark, Kevin, Paul, Bailey, Jalani, Ellen, Ryan, Costin, Sidu, Ved, Kevin, Carl, Lisa, Amna, Michelle, Ramya, Chara, Robi, Andrew, Justin, and all others. Thank you for your continued support and companionship through this journey. Grad school would have been an altogether different and darker time without you. To my family: Dad, Mom, Alex, Aidan, Aunt Lyn Sue, Grandma, Halmoni, and everyone else. Thank you for loving and supporting me since the very beginning, and for instilling in me an innate curiosity and love of learning. I owe you everything, and hope to make you proud. To Soyeun. Last but certainly not least, thank you for your unwavering support through the highs and lows of grad school. I truly could not have done it without your invariably sage advice, spot-on presentation notes, and emotional and moral support. viii Contents 0 Introduction1 0.1 Structure....................................3 1 Liquid Democracy7 1.1 An Algorithmic Perspective on Liquid Democracy..............7 1.1.1 Overview of the Model and Results..................8 1.1.2 Related Work..............................9 1.1.3 The Model................................ 10 1.1.4 Impossibility for Local Mechanisms.................. 12 1.1.5 Possibility for Non-Local Mechanisms................. 20 1.2 Minimizing the Maximum Weight of Voters in Liquid Democracy..... 29 1.2.1 Our Approach and Results....................... 30 1.2.2 Related Work.............................. 31 1.2.3 Algorithmic Model and Results.................... 32 1.2.4 Probabilistic Model and Results.................... 38 1.2.5 Simulations............................... 46 1.3 Conclusions................................... 51 1.3.1 An Algorithmic Perspective on Liquid Democracy.......... 51 1.3.2 Minimizing the Maximum Weight of Voters............. 52 2 District-Fair Participatory Budgeting 55 2.1 Introduction................................... 55 2.2 Related Work.................................. 57 2.3 Formal Problem, Notation and Definitions.................. 58 2.3.1 NP-Hardness.............................. 59 2.4 Optimal District-Fair Lottery......................... 60 2.5 Optimal DF1 Outcome with Extra Budget.................. 63 2.6 Conclusions................................... 66 3 Representation in Multiwinner Elections 69 3.1 Introduction................................... 69 3.2 Related Work.................................. 70 3.3 Preliminaries.................................. 71 3.4 Justified Representation in VNW Elections.................. 74 ix 3.5 Deterministic Rules............................... 75 3.6 Randomized Rules............................... 76 3.7 Conclusions................................... 79 4 Virtual Democracy 81 4.1 Virtual Democracy in Theory......................... 81 4.1.1 Related Work.............................. 83 4.1.2 Preliminaries.............................. 84 4.1.3 From Predictions to Mallows...................... 85 4.1.4 Robustness of Borda Count...................... 87 4.1.5 Non-Robustness of PMC Rules.................... 90 4.1.6 Empirical Results............................ 91 4.2 Virtual Democracy in Practice: 412 Food Rescue.............. 93 4.2.1 Introduction............................... 93 4.2.2 Governing Algorithm Design and Participation............ 95 4.2.3 The WeBuildAI Framework...................... 98 4.2.4 Case study: Matching algorithm for donation allocation....... 100 4.2.5 Individual Belief Model Building................... 104 4.2.6 Collective aggregation......................... 108 4.2.7 Explanation and decision support................... 109 4.2.8 Findings: the impact of participatory algorithm design....... 110 4.2.9 Evaluation of Algorithmic Outcomes................. 115 4.2.10 Discussion................................ 118 4.3 Conclusions................................... 122 4.3.1 Virtual Democracy, in Theory..................... 122 4.3.2 Virtual Democracy, in Practice: WeBuildAI............. 122 5 Impartial Ranking 125 5.1 Impartial Ranking, in Theory......................... 125 5.1.1 Our Approach and Results....................... 126 5.1.2 Related Work.............................. 127 5.1.3 Preliminaries.............................. 127 5.1.4 Measures of Error............................ 128 5.1.5 The k-Partite Algorithm....................... 130 5.1.6 The Committee Algorithm...................... 133 5.1.7 Experiments............................... 134 5.2 Impartial
Load more

Recommended publications
  • Critical Strategies Under Approval Voting: Who Gets Ruled in and Ruled Out
    Critical Strategies Under Approval Voting: Who Gets Ruled In And Ruled Out Steven J. Brams Department of Politics New York University New York, NY 10003 USA [email protected] M. Remzi Sanver Department of Economics Istanbul Bilgi University 80310, Kustepe, Istanbul TURKEY [email protected] January 2005 2 Abstract We introduce the notion of a “critical strategy profile” under approval voting (AV), which facilitates the identification of all possible outcomes that can occur under AV. Included among AV outcomes are those given by scoring rules, single transferable vote, the majoritarian compromise, Condorcet systems, and others as well. Under each of these systems, a Condorcet winner may be upset through manipulation by individual voters or coalitions of voters, whereas AV ensures the election of a Condorcet winner as a strong Nash equilibrium wherein voters use sincere strategies. To be sure, AV may also elect Condorcet losers and other lesser candidates, sometimes in equilibrium. This multiplicity of (equilibrium) outcomes is the product of a social-choice framework that is more general than the standard preference-based one. From a normative perspective, we argue that voter judgments about candidate acceptability should take precedence over the usual social-choice criteria, such as electing a Condorcet or Borda winner. Keywords: approval voting; elections; Condorcet winner/loser; voting games; Nash equilibrium. Acknowledgments. We thank Eyal Baharad, Dan S. Felsenthal, Peter C. Fishburn, Shmuel Nitzan, Richard F. Potthoff, and Ismail Saglam for valuable suggestions. 3 1. Introduction Our thesis in this paper is that several outcomes of single-winner elections may be socially acceptable, depending on voters’ individual views on the acceptability of the candidates.
    [Show full text]
  • A Liquid Democracy System for Human-Computer Societies
    A Liquid Democracy System for Human-Computer Societies Anton Kolonin, Ben Goertzel, Cassio Pennachin, Deborah Duong, Marco Argentieri, Matt Iklé, Nejc Znidar SingularityNET Foundation, Amsterdam, Netherlands {anton, ben, cassio}@singularitynet.io Abstract replicated in latest developments of distributed computing system based on Proof-of-Stake (PoS) in blockchain. In the Problem of reliable democratic governance is blockchain systems, including some that are now used to critical for survival of any community, and it will design ecosystems for Artificial Intelligence (AI) be critical for communities powered with Artificial applications, the mostly suggested solution called Delegated Intelligence (AI) systems upon developments of Proof-of-Stake (DPoS), which effectively means that rule on the latter. Apparently, it will be getting more and basis of financial capabilities while it is implemented more critical because of increasing speeds and indirectly, by means of manually controlled voting process scales of electronic communications and to select delegates to conduct the governance of the system. decreasing latencies in system responses. In order The latter be only limited improvement and can nor be to address this need, we present design and implemented in AI communities operating at high speeds implementation of a reputation system supporting not controllable by means of limited human capabilities. “liquid democracy” principle. The system is based on “weighted liquid rank” algorithm employing The described situation leads to the danger that consensus in different sorts of explicit and implicit ratings being any emergent AI community may be quickly took over by exchanged by members of the society as well as AI system hostile to either majority of community of AI implicit assessments of of the members based on systems or humans that are supposed to be served by given measures of their activity in the society.
    [Show full text]
  • Direct E-Democracy and Political Party Websites: in the United States and Sweden
    Rochester Institute of Technology RIT Scholar Works Theses 5-1-2015 Direct E-Democracy and Political Party Websites: In the United States and Sweden Kirk M. Winans Follow this and additional works at: https://scholarworks.rit.edu/theses Recommended Citation Winans, Kirk M., "Direct E-Democracy and Political Party Websites: In the United States and Sweden" (2015). Thesis. Rochester Institute of Technology. Accessed from This Thesis is brought to you for free and open access by RIT Scholar Works. It has been accepted for inclusion in Theses by an authorized administrator of RIT Scholar Works. For more information, please contact [email protected]. Running head: E-DEMOCRACY AND POLITICAL PARTY WEBSITES Direct E-Democracy and Political Party Websites: In the United States and Sweden by Kirk M. Winans Thesis Submitted in Partial Fulfillment of the Graduation Requirements for the Degree of Master of Science Science, Technology and Public Policy Department of Public Policy College of Liberal Arts Rochester Institute of Technology May 1, 2015 E-DEMOCRACY AND POLITICAL PARTY WEBSITES Direct E-Democracy and Political Party Websites: In the United States and Sweden A thesis submitted to The Public Policy Department at Rochester Institute of Technology By Kirk M. Winans Under the faculty guidance of Franz Foltz, Ph.D. Submitted by: Kirk M. Winans Signature Date Accepted by: Dr. Franz Foltz Thesis Advisor, Graduate Coordinator Signature Date Associate Professor, Dept. of STS/Public Policy Rochester Institute of Technology Dr. Rudy Pugliese Committee Member Signature Date Professor, School of Communication Rochester Institute of Technology Dr. Ryan Garcia Committee Member Signature Date Assistant Professor, Dept.
    [Show full text]
  • Are Condorcet and Minimax Voting Systems the Best?1
    1 Are Condorcet and Minimax Voting Systems the Best?1 Richard B. Darlington Cornell University Abstract For decades, the minimax voting system was well known to experts on voting systems, but was not widely considered to be one of the best systems. But in recent years, two important experts, Nicolaus Tideman and Andrew Myers, have both recognized minimax as one of the best systems. I agree with that. This paper presents my own reasons for preferring minimax. The paper explicitly discusses about 20 systems. Comments invited. [email protected] Copyright Richard B. Darlington May be distributed free for non-commercial purposes Keywords Voting system Condorcet Minimax 1. Many thanks to Nicolaus Tideman, Andrew Myers, Sharon Weinberg, Eduardo Marchena, my wife Betsy Darlington, and my daughter Lois Darlington, all of whom contributed many valuable suggestions. 2 Table of Contents 1. Introduction and summary 3 2. The variety of voting systems 4 3. Some electoral criteria violated by minimax’s competitors 6 Monotonicity 7 Strategic voting 7 Completeness 7 Simplicity 8 Ease of voting 8 Resistance to vote-splitting and spoiling 8 Straddling 8 Condorcet consistency (CC) 8 4. Dismissing eight criteria violated by minimax 9 4.1 The absolute loser, Condorcet loser, and preference inversion criteria 9 4.2 Three anti-manipulation criteria 10 4.3 SCC/IIA 11 4.4 Multiple districts 12 5. Simulation studies on voting systems 13 5.1. Why our computer simulations use spatial models of voter behavior 13 5.2 Four computer simulations 15 5.2.1 Features and purposes of the studies 15 5.2.2 Further description of the studies 16 5.2.3 Results and discussion 18 6.
    [Show full text]
  • MGF 1107 FINAL EXAM REVIEW CHAPTER 9 1. Amy (A), Betsy
    MGF 1107 FINAL EXAM REVIEW CHAPTER 9 1. Amy (A), Betsy (B), Carla (C), Doris (D), and Emilia (E) are candidates for an open Student Government seat. There are 110 voters with the preference lists below. 36 24 20 18 8 4 A E D B C C B C E D E D C B C C B B D D B E D E E A A A A A Who wins the election if the method used is: a) plurality? b) plurality with runoff? c) sequential pairwise voting with agenda ABEDC? d) Hare system? e) Borda count? 2. What is the minimum number of votes needed for a majority if the number of votes cast is: a) 120? b) 141? 3. Consider the following preference lists: 1 1 1 A C B B A D D B C C D A If sequential pairwise voting and the agenda BACD is used, then D wins the election. Suppose the middle voter changes his mind and reverses his ranking of A and B. If the other two voters have unchanged preferences, B now wins using the same agenda BACD. This example shows that sequential pairwise voting fails to satisfy what desirable property of a voting system? 4. Consider the following preference lists held by 5 voters: 2 2 1 A B C C C B B A A First, note that if the plurality with runoff method is used, B wins. Next, note that C defeats both A and B in head-to-head matchups. This example shows that the plurality with runoff method fails to satisfy which desirable property of a voting system? 5.
    [Show full text]
  • On the Distortion of Voting with Multiple Representative Candidates∗
    The Thirty-Second AAAI Conference on Artificial Intelligence (AAAI-18) On the Distortion of Voting with Multiple Representative Candidates∗ Yu Cheng Shaddin Dughmi David Kempe Duke University University of Southern California University of Southern California Abstract voters and the chosen candidate in a suitable metric space (Anshelevich 2016; Anshelevich, Bhardwaj, and Postl 2015; We study positional voting rules when candidates and voters Anshelevich and Postl 2016; Goel, Krishnaswamy, and Mu- are embedded in a common metric space, and cardinal pref- erences are naturally given by distances in the metric space. nagala 2017). The underlying assumption is that the closer In a positional voting rule, each candidate receives a score a candidate is to a voter, the more similar their positions on from each ballot based on the ballot’s rank order; the candi- key questions are. Because proximity implies that the voter date with the highest total score wins the election. The cost would benefit from the candidate’s election, voters will rank of a candidate is his sum of distances to all voters, and the candidates by increasing distance, a model known as single- distortion of an election is the ratio between the cost of the peaked preferences (Black 1948; Downs 1957; Black 1958; elected candidate and the cost of the optimum candidate. We Moulin 1980; Merrill and Grofman 1999; Barbera,` Gul, consider the case when candidates are representative of the and Stacchetti 1993; Richards, Richards, and McKay 1998; population, in the sense that they are drawn i.i.d. from the Barbera` 2001). population of the voters, and analyze the expected distortion Even in the absence of strategic voting, voting systems of positional voting rules.
    [Show full text]
  • Stable Voting
    Stable Voting Wesley H. Hollidayy and Eric Pacuitz y University of California, Berkeley ([email protected]) z University of Maryland ([email protected]) September 12, 2021 Abstract In this paper, we propose a new single-winner voting system using ranked ballots: Stable Voting. The motivating principle of Stable Voting is that if a candidate A would win without another candidate B in the election, and A beats B in a head-to-head majority comparison, then A should still win in the election with B included (unless there is another candidate A0 who has the same kind of claim to winning, in which case a tiebreaker may choose between A and A0). We call this principle Stability for Winners (with Tiebreaking). Stable Voting satisfies this principle while also having a remarkable ability to avoid tied outcomes in elections even with small numbers of voters. 1 Introduction Voting reform efforts in the United States have achieved significant recent successes in replacing Plurality Voting with Instant Runoff Voting (IRV) for major political elections, including the 2018 San Francisco Mayoral Election and the 2021 New York City Mayoral Election. It is striking, by contrast, that Condorcet voting methods are not currently used in any political elections.1 Condorcet methods use the same ranked ballots as IRV but replace the counting of first-place votes with head- to-head comparisons of candidates: do more voters prefer candidate A to candidate B or prefer B to A? If there is a candidate A who beats every other candidate in such a head-to-head majority comparison, this so-called Condorcet winner wins the election.
    [Show full text]
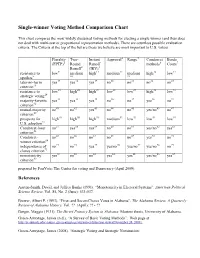
  • Single-Winner Voting Method Comparison Chart
    Single-winner Voting Method Comparison Chart This chart compares the most widely discussed voting methods for electing a single winner (and thus does not deal with multi-seat or proportional representation methods). There are countless possible evaluation criteria. The Criteria at the top of the list are those we believe are most important to U.S. voters. Plurality Two- Instant Approval4 Range5 Condorcet Borda (FPTP)1 Round Runoff methods6 Count7 Runoff2 (IRV)3 resistance to low9 medium high11 medium12 medium high14 low15 spoilers8 10 13 later-no-harm yes17 yes18 yes19 no20 no21 no22 no23 criterion16 resistance to low25 high26 high27 low28 low29 high30 low31 strategic voting24 majority-favorite yes33 yes34 yes35 no36 no37 yes38 no39 criterion32 mutual-majority no41 no42 yes43 no44 no45 yes/no 46 no47 criterion40 prospects for high49 high50 high51 medium52 low53 low54 low55 U.S. adoption48 Condorcet-loser no57 yes58 yes59 no60 no61 yes/no 62 yes63 criterion56 Condorcet- no65 no66 no67 no68 no69 yes70 no71 winner criterion64 independence of no73 no74 yes75 yes/no 76 yes/no 77 yes/no 78 no79 clones criterion72 81 82 83 84 85 86 87 monotonicity yes no no yes yes yes/no yes criterion80 prepared by FairVote: The Center for voting and Democracy (April 2009). References Austen-Smith, David, and Jeffrey Banks (1991). “Monotonicity in Electoral Systems”. American Political Science Review, Vol. 85, No. 2 (June): 531-537. Brewer, Albert P. (1993). “First- and Secon-Choice Votes in Alabama”. The Alabama Review, A Quarterly Review of Alabama History, Vol. ?? (April): ?? - ?? Burgin, Maggie (1931). The Direct Primary System in Alabama.
    [Show full text]
  • Interactive Democracy Blue Sky Ideas Track
    Session 29: Blue Sky AAMAS 2018, July 10-15, 2018, Stockholm, Sweden Interactive Democracy Blue Sky Ideas Track Markus Brill TU Berlin Berlin, Germany [email protected] ABSTRACT approached this question by developing an app, DemocracyOS [48], Interactive Democracy is an umbrella term that encompasses a va- that allows users to propose, debate, and vote on issues. Democ- riety of approaches to make collective decision making processes racyOS is only one example of a quickly growing number of ap- more engaging and responsive. A common goal of these approaches proaches that aim to reconcile established democratic processes is to utilize modern information technology—in particular, the with the desire of citizens to participate in political decision mak- 1 Internet—in order to enable more interactive decision making pro- ing. Another example is the software LiquidFeedback [6], which is 2 cesses. An integral part of many interactive democracy proposals developed by the Association for Interactive Democracy. Currently, are online decision platforms that provide much more flexibility these tools are mainly used for decision making within progressive and interaction possibilities than traditional democratic systems. political parties [9, p. 162] or in the context of community engage- This is achieved by embracing the novel paradigm of delegative ment platforms such as WeGovNow [10]. A common goal of these voting, often referred to as liquid democracy, which aims to recon- approaches, often summarized under the umbrella term Interac- 3 cile the idealistic appeal of direct democracy with the practicality tive Democracy (henceforth ID), is to utilize modern information of representative democracy. The successful design of interactive technology—in particular, the Internet—in order to enable more democracy systems presents a multidisciplinary research challenge; interactive decision making processes.
    [Show full text]
  • Democracy on the Precipice Council of Europe Democracy 2011-12 Council of Europe Publishing Debates
    Democracy on the Precipice Democracy Democracy is well-established and soundly practiced in most European countries. But despite unprecedented progress, there is growing dissatisfaction with the state of democracy and deepening mistrust of democratic institutions; a situation exacer- Democracy on the Precipice bated by the economic crisis. Are Europe’s democracies really under threat? Has the traditional model of European democracy exhausted its potential? A broad consensus is forming as to the urgent need to examine the origins of the crisis and to explore Council of Europe visions and strategies which could contribute to rebuilding confidence in democracy. Democracy Debates 2011-12 As Europe’s guardian of democracy, human rights and the rule of law, the Council of Europe is committed to exploring the state and practice of European democracy, as Debates of Europe Publishing 2011-12 Council Council of Europe Democracy well as identifying new challenges and anticipating future trends. In order to facilitate Preface by Thorbjørn Jagland this reflection, the Council of Europe held a series of Democracy Debates with the participation of renowned specialists working in a variety of backgrounds and disciplines. This publication presents the eight Democracy Debate lectures. Each presentation Zygmunt Bauman analyses a specific aspect of democracy today, placing the issues not only in their political context but also addressing the historical, technological and communication Ulrich Beck dimensions. The authors make proposals on ways to improve democratic governance Ayşe Kadıoğlu and offer their predictions on how democracy in Europe may evolve. Together, the presentations contribute to improving our understanding of democracy today and to John Keane recognising the ways it could be protected and strengthened.
    [Show full text]
  • The Fluid Mechanics of Liquid Democracy
    The Fluid Mechanics of Liquid Democracy Paul Gölz Anson Kahng Simon Mackenzie Ariel D. Procaccia Abstract Liquid democracy is the principle of making collective decisions by letting agents transitively delegate their votes. Despite its significant appeal, it has become apparent that a weakness of liquid democracy is that a small subset of agents may gain massive influence. To address this, we propose to change the current practice by allowing agents to specify multiple delegation options instead of just one. Much like in nature, where — fluid mechanics teaches us — liquid maintains an equal level in connected vessels, so do we seek to control the flow of votes in a way that balances influence as much as possible. Specifically, we analyze the problem of choosing delegations to approximately minimize the maximum number of votes entrusted to any agent, by drawing connections to the literature on confluent flow. We also introduce a random graph model for liquid democracy, and use it to demonstrate the benefits of our approach both theoretically and empirically. 1 Introduction Liquid democracy is a potentially disruptive approach to democratic decision making. As in direct democracy, agents can vote on every issue by themselves. Alternatively, however, agents may delegate their vote, i.e., entrust it to any other agent who then votes on their behalf. Delegations are transitive; for example, if agents 2 and 3 delegate their votes to 1, and agent 4 delegates her vote to 3, then agent 1 would vote with the weight of all four agents, including herself. Just like representative democracy, this system allows for separation of labor, but provides for stronger accountability: Each delegator is connected to her transitive delegate by a path of personal trust relationships, and each delegator on this path can withdraw her delegation at any time if she disagrees with her delegate’s choices.
    [Show full text]
  • A Brief Introductory T T I L C T Ti L Tutorial on Computational Social Choice
    A Brief Introductory TtTutori ilal on Compu ttitationa l Social Choice Vincent Conitzer Outline • 1. Introduction to votinggy theory • 2. Hard-to-compute rules • 3. Using computational hardness to prevent manipulation and other undesirable behavior in elections • 4. Selected topics (time permitting) Introduction to voting theory Voting over alternatives voting rule > > (mechanism) determines winner based on votes > > • Can vote over other things too – Where to ggg,jp,o for dinner tonight, other joint plans, … Voting (rank aggregation) • Set of m candidates (aka. alternatives, outcomes) •n voters; each voter ranks all the candidates – E.g., for set of candidates {a, b, c, d}, one possible vote is b > a > d > c – Submitted ranking is called a vote • AvotingA voting rule takes as input a vector of votes (submitted by the voters), and as output produces either: – the winning candidate, or – an aggregate ranking of all candidates • Can vote over just about anything – pppolitical representatives, award nominees, where to go for dinner tonight, joint plans, allocations of tasks/resources, … – Also can consider other applications: e.g., aggregating search engines’ rankinggggs into a single ranking Example voting rules • Scoring rules are defined by a vector (a1, a2, …, am); being ranked ith in a vote gives the candidate ai points – Plurality is defined by (1, 0, 0, …, 0) (winner is candidate that is ranked first most often) – Veto (or anti-plurality) is defined by (1, 1, …, 1, 0) (winner is candidate that is ranked last the least often) – Borda is defined by (m-1, m-2, …, 0) • Plurality with (2-candidate) runoff: top two candidates in terms of plurality score proceed to runoff; whichever is ranked higher than the other by more voters, wins • Single Transferable Vote (STV, aka.
    [Show full text]