Interactive Dimensioning of Parametric Models T
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Iot4cps Deliverable
IoT4CPS – Trustworthy IoT for CPS FFG - ICT of the Future Project No. 863129 Deliverable D5.1 Lifecycle Data Models for Smart Automotive and Smart Manufacturing Deliverable number: D5.1 Dissemination level: Public Delivery data: 13. June 2018 Editor: Violeta Damjanovic-Behrendt Author(s): Violeta Damjanovic-Behrendt (SRFG) Michaela Mühlberger (SRFG) Cristina de Luca (IFAT) Thomos Christos (IFAT) Reviewers: Heinz Weiskirchner (NOKIA) Edin Arnautovic (TTTech) The IoT4CPS project is partially funded by the “ICT of the Future” Program of the FFG and the BMVIT. The IoT4CPS Consortium: IoT4CPS – 863129 Lifecycle Data Models for Smart Automotive and Smart Manufacturing AIT – Austrian Institute of Technology GmbH AVL – AVL List GmbH DUK – Donau-Universität Krems IFAT – Infineon Technologies Austria AG JKU – JK Universität Linz / Institute for Pervasive Computing JR – Joanneum Research Forschungsgesellschaft mbH NOKIA – Nokia Solutions and Networks Österreich GmbH NXP – NXP Semiconductors Austria GmbH SBA – SBA Research GmbH SRFG – Salzburg Research Forschungsgesellschaft SCCH – Software Competence Center Hagenberg GmbH SAGÖ – Siemens AG Österreich TTTech – TTTech Computertechnik AG IAIK – TU Graz / Institute for Applied Information Processing and Communications ITI – TU Graz / Institute for Technical Informatics TUW – TU Wien / Institute of Computer Engineering XNET – X-Net Services GmbH Document Control Title: Lifecycle Data Models for Smart Automotive and Smart Manufacturing Type: Public Editor(s): Violeta Damjanovic-Behrendt Author(s): Violeta -

Development of Line Width and Type Control of 2D Cad Software Based on Iso Technical Drawing Standard
UNIVERSITI PUTRA MALAYSIA DEVELOPMENT OF LINE WIDTH AND TYPE CONTROL OF 2D CAD SOFTWARE BASED ON ISO TECHNICAL DRAWING STANDARD PITOON NOPNAKORN FK 2003 44 DEVELOPMENT OF LINE WIDTH AND TYPE CONTROL OF 2D CAD SOFTWARE BASED ON ISO TECHNICAL DRAWING STANDARD By PITOON NOPNAKORN Thesis Submitted to the School of Graduate Studies, Universiti Putra Malaysia, in Fulfilmentof the Requirements for the Degree of Master of Science October 2003 DEDICATION To My Parents One who ever shared a moment of his love and one who has strived patiently fo r their beloved children 11 Abstract of the thesispresented to theSenate ofUniversiti Putra Malaysia in fulfilmentof the requirements fo r the degree of Master of Science DEVELOPMENT OF LINE WIDTH AND TYPE CONTROL OF 2D CAD SOFTWARE BASED ON ISO TECHNICAL DRAWING STANDARD By PITOON NOPNAKORN October 2003 Chairman: Associate Professor Napsiah Ismail, Ph.D. Faculty: Engineering Engineering drawing is the media of communication in manufacturing process. In order to communicate in the same graphic language in engineering, the technical drawing standard has been specified by the International Organization fo r Standardization (ISO). Some commercial CAD softwares such as AutoCAD, AutoSketch and Solid Edge provided high-end ability to work whether in 3D or 2D space. Their width, length and proportion of printed lines conform to the ISO Technical Drawing Standard. But the procedures and interface to create line width and line type fo r simple drawing are sometime tedious and complex. The aim of this research work is to develop a 2D CAD software with emphasize on line width and line type control based on the ISO technical drawing standard fo r technical drawing. -

Development of a New Drawing System for STS
School of Innovation, Design and Engineering BACHELOR THESIS IN AERONAUTICAL ENGINEERING 15 CREDITS, BASIC LEVEL 300 Development of a new drawing system for STS Authors: Mikael Berkelund and Christian Håkonsen Report code: MDH.IDT.FLYG.0189.2008.GN300.15HP.D. Abstract An engineering firm which handles and constructs drawings needs well defined routines and structures which should be homogeneous through all the different departments. A common drawing system results in better quality and cooperation between the departments. SAS Technical Services (STS) did not have a common drawing system which had led to development of different routines in the different regions and departments. Requested was development of new routines regarding engineering drawings, such as drawing numbering structure, revision and subscription routines, which standards to adhere to, custom made drawing templates and management of the drawings with belonging documents. Each requested task was broken into minor tasks and analyzed. Solutions by different leading engineering companies were used for comparison and ideas. All the tasks were collected and organized in one single document which is the result of the thesis; a drawing instruction. The drawing instruction will after a learning phase ease the work for the STS engineers as all necessary information can be found in one single place. Also, work with contractors will be time-saving as the instruction can be handed out for guidance. Date: 29 jan 2008 Carried out at: SAS Technical Services Advisor at MDH: Tommy Nygren Advisor at SAS Technical Services: Anders Pramler Examinator: Gustaf Enebog II Sammanfattning En ingenjörsfirma som hanterar och skapar mängder med ritningar behöver väldefinierade rutiner och strukturer som är homogena genom hela bolaget. -

Industrial Automation
ISO Focus The Magazine of the International Organization for Standardization Volume 4, No. 12, December 2007, ISSN 1729-8709 Industrial automation • Volvo’s use of ISO standards • A new generation of watches Contents 1 Comment Alain Digeon, Chair of ISO/TC 184, Industrial automation systems and integration, starting January 2008 2 World Scene Highlights of events from around the world 3 ISO Scene Highlights of news and developments from ISO members 4 Guest View ISO Focus is published 11 times Katarina Lindström, Senior Vice-President, a year (single issue : July-August). It is available in English. Head of Manufacturing in Volvo Powertrain and Chairman of the Manufacturing, Key Technology Committee Annual subscription 158 Swiss Francs Individual copies 16 Swiss Francs 8 Main Focus Publisher • Product data – ISO Central Secretariat Managing (International Organization for information through Standardization) the lifecycle 1, ch. de la Voie-Creuse CH-1211 Genève 20 • Practical business Switzerland solutions for ontology Telephone + 41 22 749 01 11 data exchange Fax + 41 22 733 34 30 • Modelling the E-mail [email protected] manufacturing enterprise Web www.iso.org • Improving productivity Manager : Roger Frost with interoperability Editor : Elizabeth Gasiorowski-Denis • Towards integrated Assistant Editor : Maria Lazarte manufacturing solutions Artwork : Pascal Krieger and • A new model for machine data transfer Pierre Granier • The revolution in engineering drawings – Product definition ISO Update : Dominique Chevaux data sets Subscription enquiries : Sonia Rosas Friot • A new era for cutting tools ISO Central Secretariat • Robots – In industry and beyond Telephone + 41 22 749 03 36 Fax + 41 22 749 09 47 37 Developments and Initiatives E-mail [email protected] • A new generation of watches to meet consumer expectations © ISO, 2007. -

Andreas Degen
Andreas Degen Plattenfeld 2a ● 85244 Roehrmoos ● Germany ++49 – 160 – 9163-5114 ● [email protected] ● www.andreasdegen.de Main Accomplishments Designed and programmed a simulation to expose the functionality of the new developed Instrument Cluster (SL, SLK, etc.) to Dr. Zetsche Developed a 2 Electrode ECG-Amplifier circuit for an Activity Sensor to use for patient monitoring to increase the possibility to detect a my- ocardial infarction Implemented INTERBUS-S as a measurement system at the Mainzer Microtron and its spectrometers and also wrote the programming tools for the IT department to use INTERBUS-S Programmed an ERP-System for the Purchasing Department of the In- stitute of Nuclear Physics of the University of Mainz to increase the ef- ficiency of the Institute Employment History 01/2012 – current QC Engineer, Business Unit BMW ALPINE ELECTRONICS GmbH, Munich Responsible for the Product Quality of all Displays for BMW (SOP) Main point of contact for QM-Topics for customer Negotiation of the Year End Invoice with BMW warranty Control / release of the 8D-reports from China / Hungary plants Technologies: SPC, Automotive SPICE, Lotus Notes, B2B 09/2010 – 01/2011 Product Development Engineer Electronics (Interior) Kongsberg Automotive GmbH, Munich Design & Development of electronic hardware and software Active member of the new project introduction team being re- sponsible for the electronic application engineering Assist the plant quality and process engineering department Technologies: CANape, CANoe, VAS Andreas Degen Page 1 of 6 11/2007 – 08/2010 Resident Engineer Ruecker GmbH (CCE), Wiesbaden Working as a Software Resident Engineer for “Robert Bosch GmbH” at “Daimler AG” (Development of Instrument Cluster) Requirements-, Change- and Error Management Main point of contact for SW-Topics for customer Working in SW-Jour Fixe, SW-Meeting, Specification Review Assistance to the Software project manager and the Software developer team Enhancement of the CANoe Simulation (e.g. -

International Standard Iso 128-1:2020(E)
INTERNATIONAL ISO STANDARD 128-1 Second edition 2020-05 Technical product documentation (TPD) — General principles of representation — Part 1: Introduction and fundamental iTeh STrequirementsANDARD PREVIEW Documentation technique de produits (TPD) — Principes généraux de (streprésentationandards —.iteh.ai) PartieI S1:O Introduction 128-1:2020 et exigences fondamentales https://standards.iteh.ai/catalog/standards/sist/62506fd1-da5a-4ce9-ba04- 890d8478a389/iso-128-1-2020 Reference number ISO 128-1:2020(E) © ISO 2020 ISO 128-1:2020(E) iTeh STANDARD PREVIEW (standards.iteh.ai) ISO 128-1:2020 https://standards.iteh.ai/catalog/standards/sist/62506fd1-da5a-4ce9-ba04- 890d8478a389/iso-128-1-2020 COPYRIGHT PROTECTED DOCUMENT © ISO 2020 All rights reserved. Unless otherwise specified, or required in the context of its implementation, no part of this publication may be reproduced or utilized otherwise in any form or by any means, electronic or mechanical, including photocopying, or posting on the internet or an intranet, without prior written permission. Permission can be requested from either ISO at the address belowCP 401or ISO’s • Ch. member de Blandonnet body in 8 the country of the requester. ISO copyright office Phone: +41 22 749 01 11 CH-1214 Vernier, Geneva Fax:Website: +41 22www.iso.org 749 09 47 PublishedEmail: [email protected] Switzerland ii © ISO 2020 – All rights reserved ISO 128-1:2020(E) Contents Page Foreword ........................................................................................................................................................................................................................................iv -
STANDARDS LIST Neu.Xlsx
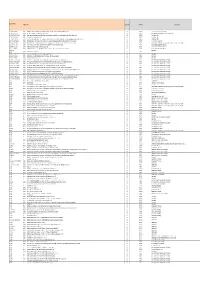
Document‐Number Published Title Organization Committee Committee Title IEC 100/2536/CD * IEC 63002 2015‐07 IEC 63002, Ed. 1.0: Idenficaon and CommunicaonInteroperability Method for External Power Supplies Used WithPortable Compung Devices (TA 14) IEC IEC/TC 100 Audio, video and multimedia systems and equipment IEC 115/105/CD *IEC/TR 62978 2015‐01 IEC/TR 62978, Ed. 1: Guidelines on Asset Management forHVDC Installaons IEC IEC/TC 115 High Voltage Direct Current (HVDC) transmission for DC voltages above 100 kV IEC 118/29/DPAS* IEC/PAS 62746‐199 2013‐09 System interfaces and communication protocol profiles relevant for systems connected to the smart grid ‐ Open Automated Demand Response (OpenADR 2.0 Profile Specification) IEC IEC/PC 118 Smart grid user interface IEC 118/46/CD *IEC 62746‐10‐2 2014‐12 OASIS Energy Interoperation Version 1.0 Specification IEC IEC/PC 118 Smart grid user interface IEC 118/47/CD * IEC 62746‐10‐1 2015‐01 IEC 62746‐10‐1: Systems interface between customer energymanagement system and the power management system ‐ Part10 ‐1: Open Automated Demand Response (OpenADR 2.0bPro file Specificaon) IEC IEC/PC 118 Smart grid user interface IEC 22H/192/CD * IEC/TS 62040‐4‐1 2015‐04 IEC/TS 62040‐4‐1: Uninterrupble power systems (UPS) ‐ Part 4‐1: Environmental aspects ‐ Product Category Rules (PCR) for life Cycle Assessment and environmental declaraons IEC IEC/SC 22H Uninterruptible power systems (UPS) IEC 3/1224A/CD * IEC 81346‐2 2015‐05 Industrial systems, installaons and equipment and industrialproducts ‐ Structuring principles and reference designaons ‐ Part 2: Classificaon of objects and codes for classes IEC IEC/TC 3 Information structures and elements, identification and marking principles, documentation and graphical symbols IEC 3D/225A/CD * IEC 62656‐5 2014‐03 IEC 62656‐5, Ed. -

Geometric Dimensioning and Tolerancing
Geometric dimensioning and tolerancing Geometric Dimensioning and Tolerancing (GD&T) is a system for defining and communicating engineering tolerances. It uses a symbolic language on engineering drawings and computer-generated three-dimensional solid models that explicitly describes nominal geometry and its allowable variation. It tells the manufacturing staff and machines what degree of accuracy and precision is needed on each controlled feature of the part. GD&T is used to define the nominal (theoretically perfect) geometry of parts and assemblies, to define the allowable variation in form and possible size of individual features, and to define the allowable variation between features. Dimensioning specifications define the nominal, as-modeled or as-intended geometry. One example is a basic dimension. Example of geometric dimensioning Tolerancing specifications define the allowable variation for the form and possibly the size of individual features, and and tolerancing the allowable variation in orientation and location between features. woT examples are linear dimensions and feature control frames using adatum reference (both shown above). There are several standards available worldwide that describe the symbols and define the rules used in GD&T. One such standard is American Society of Mechanical Engineers (ASME) Y14.5-2009. This article is based on that standard, but other standards, such as those from the International Organization for Standardization (ISO), may vary slightly. The Y14.5 standard has the advantage of providing a fairly complete set of standards for GD&T in one document. The ISO standards, in comparison, typically only address a single topic at a time. There are separate standards that provide the details for each of the major symbols and topics below (e.g. -

The Interplay of Public and Private Standards Literature Review Series on the Impacts of Private Standards – Part Iii
TECHNICAL PAPER THE INTERPLAY OF PUBLIC AND PRIVATE STANDARDS LITERATURE REVIEW SERIES ON THE IMPACTS OF PRIVATE STANDARDS – PART III THE INTERPLAY OF PUBLIC AND PRIVATE STANDARDS LITERATURE REVIEW SERIES ON THE IMPACTS OF PRIVATE STANDARDS – PART III THE INTERPLAY OF PUBLIC AND PRIVATE STANDARDS Abstract for trade information services ID=42694 2011 F-09.03.01 INT International Trade Centre (ITC) The Interplay of Public and Private Standards. Geneva: ITC, 2011. x, 41 p. (Literature Review Series on the Impacts of Private Standards; Part III) Doc. No. MAR-11-215.E Part three of a series of four papers, each comprising a literature review of the main information resources regarding a specific aspect of the impact of private standards focuses on the literature related to harmonization of, and interdependencies between public and private standards, and the ways in which governments could engage with private standards to impact their legitimacy and significance in the market; provides examples of complementarities between public and private standards, and the harmonization efforts made in this area. Descriptors: Standards, Private Standards, Standardization, Certification, Bibliographies. For further information on this technical paper, contact (add contact name and details) English, French, Spanish (separate editions) (verify the language or languages. If only one language, delete the others; also the brackets with separate editions) The International Trade Centre (ITC) is the joint agency of the World Trade Organization and the United Nations. ITC, Palais des Nations, 1211 Geneva 10, Switzerland (www.intracen.org) Views expressed in this paper are those of consultants and do not necessarily coincide with those of ITC, UN or WTO. -

Manual of Engineering Drawing
Manual of Engineering Drawing Manual of Engineering Drawing Second edition Colin H Simmons I.Eng, FIED, Mem ASME. Engineering Standards Consultant Member of BS. & ISO Committees dealing with Technical Product Documentation specifications Formerly Standards Engineer, Lucas CAV. Dennis E Maguire CEng. MIMechE, Mem ASME, R.Eng.Des, MIED Design Consultant Formerly Senior Lecturer, Mechanical and Production Engineering Department, Southall College of Technology City & Guilds International Chief Examiner in Engineering Drawing Elsevier Newnes Linacre House, Jordan Hill, Oxford OX2 8DP 200 Wheeler Road, Burlington MA 01803 First published by Arnold 1995 Reprinted by Butterworth-Heinemann 2001, 2002 Second edition 2004 Copyright © Colin H. Simmons and Denis E. Maguire, 2004. All rights reserved The right of Colin H. Simmons and Dennis E. Maguire to be identified as the authors of this work has been asserted in accordance with the Copyright, Designs and Patents Act 1988 No part of this publication may be reproduced in any material form (including photocopying or storing in any medium by electronic means and whether or not transiently or incidentally to some other use of this publication) without the written permission of the copyright holder except in accordance with the provisions of the Copyright, Designs and Patents Act 1988 or under the terms of a licence issued by the Copyright Licensing Agency Ltd, 90 Tottenham Court Road, London, England W1T 4LP. Applications for the copyright holder’s written permission to reproduce any part of this publication should be addressed to the publisher Permissions may be sought directly from Elsevier’s Science and Technology Rights Department in Oxford, UK: phone: (+44) (0) 1865 843830; fax: (+44) (0) 1865 853333; e-mail: [email protected]. -

ISO 128-1:2003 Technical Drawings—General Principles of Presentation—Part 1
ISO 128-1:2003 Technical drawings—General principles of presentation—Part 1: Introduction and index • ISO 128-20:1996 Technical drawings—General principles of presentation—Part 20: Basic conventions for lines • ISO 128-21:1997 Technical drawings—General principles of presentation—Part 21: Preparation of lines by CAD systems • ISO 128-22:1999 Technical drawings—General principles of presentation—Part 22: Basic conventions and applications for leader lines and reference lines • ISO 128-23:1999 Technical drawings—General principles of presentation—Part 23: Lines on construction drawings • ISO 128-24:2014 Technical drawings—General principles of presentation—Part 24: Lines on mechanical engineering drawings • ISO 128-30:2001 Technical drawings—General principles of presentation—Part 30: Basic conventions for views • ISO 128-34:2001 Technical drawings—General principles of presentation—Part 34: Views on mechanical engineering drawings • ISO 128-40:2001 Technical drawings—General principles of presentation—Part 40: Basic conventions for cuts and sections • ISO 128-44:2001 Technical drawings—General principles of presentation—Part 44: Sections on mechanical engineering drawings • ISO 128-50:2001 Technical drawings—General principles of presentation—Part 50: Basic conventions for representing areas on cuts and sections ISO 129 Technical drawings—Indication of dimensions and tolerances ISO 216 paper sizes, e.g. the A4 paper size ISO 406:1987 Technical drawings—Tolerancing of linear and angular dimensions ISO 1660:1987 Technical drawings—Dimensioning -

Interactive Dimensioning of Parametric Models
This is a repository copy of Interactive Dimensioning of Parametric Models. White Rose Research Online URL for this paper: http://eprints.whiterose.ac.uk/138600/ Version: Accepted Version Article: Kelly, T orcid.org/0000-0002-6575-3682, Wonka, P and Mueller, P (2015) Interactive Dimensioning of Parametric Models. Computer Graphics Forum, 34 (2). pp. 117-129. ISSN 0167-7055 https://doi.org/10.1111/cgf.12546 © 2015 The Author(s) Computer Graphics Forum © 2015 The Eurographics Association and John Wiley & Sons Ltd. Published by John Wiley & Sons Ltd. This is the pre-peer reviewed version of the following article: Kelly, T , Wonka, P and Mueller, P (2015) Interactive Dimensioning of Parametric Models. Computer Graphics Forum, 34 (2). pp. 117-129, which has been published in final form at https://doi.org/10.1111/cgf.12546 This article may be used for non-commercial purposes in accordance with Wiley Terms and Conditions for Use of Self-Archived Versions. Reuse Items deposited in White Rose Research Online are protected by copyright, with all rights reserved unless indicated otherwise. They may be downloaded and/or printed for private study, or other acts as permitted by national copyright laws. The publisher or other rights holders may allow further reproduction and re-use of the full text version. This is indicated by the licence information on the White Rose Research Online record for the item. Takedown If you consider content in White Rose Research Online to be in breach of UK law, please notify us by emailing [email protected] including the URL of the record and the reason for the withdrawal request.