Base-Advance Average Gary M
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

TODAY's HEADLINES AGAINST the OPPOSITION Home
ST. PAUL SAINTS (6-9) vs INDIANAPOLIS INDIANS (PIT) (9-5) LHP CHARLIE BARNES (1-0, 4.00) vs RHP JAMES MARVEL (0-0, 3.48) Friday, May 21st, 2021 - 7:05 pm (CT) - St. Paul, MN - CHS FIeld Game #16 - Home Game #10 TV: FOX9+/MiLB.TV RADIO: KFAN Plus 2021 At A Glance TODAY'S HEADLINES AGAINST THE OPPOSITION Home .....................................................4-5 That Was Last Night - The Saints got a walk-off win of their resumed SAINTS VS INDIANAPOLIS Road ......................................................2-4 game from Wednesday night, with Jimmy Kerrigan and the bottom of the Saints order manufacturing the winning run. The second game did .235------------- BA -------------.301 vs. LHP .............................................1-0 not go as well for St. Paul, where they dropped 7-3. Alex Kirilloff has vs. RHP ............................................5-9 homered in both games of his rehab assignment with the Saints. .333-------- BA W/2O ----------.300 Current Streak ......................................L1 .125 ------- BA W/ RISP------- .524 Most Games > .500 ..........................0 Today’s Game - The Saints aim to preserve a chance at a series win 9 ----------------RUNS ------------- 16 tonight against Indianapolis, after dropping two of the first three games. 2 ----------------- HR ---------------- 0 Most Games < .500 ..........................3 Charlie Barnes makes his third start of the year, and the Saints have yet 2 ------------- STEALS ------------- 0 Overall Series ..................................1-0-1 to lose a game he’s started. 5.00 ------------- ERA ----------- 3.04 Home Series ...............................0-0-1 28 ----------------- K's -------------- 32 Keeping it in the Park - Despite a team ERA of 4.66, the Saints have Away Series ................................0-1-0 not been damaged by round-trippers. -

NCAA Division I Baseball Records
Division I Baseball Records Individual Records .................................................................. 2 Individual Leaders .................................................................. 4 Annual Individual Champions .......................................... 14 Team Records ........................................................................... 22 Team Leaders ............................................................................ 24 Annual Team Champions .................................................... 32 All-Time Winningest Teams ................................................ 38 Collegiate Baseball Division I Final Polls ....................... 42 Baseball America Division I Final Polls ........................... 45 USA Today Baseball Weekly/ESPN/ American Baseball Coaches Association Division I Final Polls ............................................................ 46 National Collegiate Baseball Writers Association Division I Final Polls ............................................................ 48 Statistical Trends ...................................................................... 49 No-Hitters and Perfect Games by Year .......................... 50 2 NCAA BASEBALL DIVISION I RECORDS THROUGH 2011 Official NCAA Division I baseball records began Season Career with the 1957 season and are based on informa- 39—Jason Krizan, Dallas Baptist, 2011 (62 games) 346—Jeff Ledbetter, Florida St., 1979-82 (262 games) tion submitted to the NCAA statistics service by Career RUNS BATTED IN PER GAME institutions -

City of Richland Little League Tournament Rules 2015 City League Tournament Revision 2
City of Richland Little League Tournament Rules 2015 City League Tournament Revision 2 Rules The following Richland City Tournament rules may not conflict with the 2015 Baseball Official Regulations with Playing and Tournament Rules – commonly referred to as “The Green Book”. For circumstances not covered by these rules below “The Green Book” will be utilized. General Home team is responsible for emailing scores to [email protected] Higher seed is HOME team, if teams are same seed, the host site is the HOME team. o Home teams are responsible for field prep when two teams representing the same league are playing at their respective fields. (ie two GRLL teams are playing at the Bombing Range fields). If neither team represents the host park, the higher seed is responsible for field prep. (ie two RNLL teams playing at the Bombing Range fields) o Field prep instructions should be posted in the dugouts for reference. The league of where the game is being played is responsible for providing game balls o (GRLL when games are played on GRLL fields). o (RNLL when games are played on RNLL fields). The higher seed is responsible for Field prep . Instructions should be located in dugouts for field prep for visiting teams (GRLL teams playing at RNLL and vice versa) Official Book and Pitch count sheets will also be provided by the league where the game is being played and need to be turned in at the completion of each game. GRLL pitch count sheets and scorebook will be available at the concession stand RNLL pitch count sheets and scorebook will be available in the clubhouse Game Times All games begin at 5:30 PM Batting Cages GRLL Visiting team gets the cages from 4:15-4:45pm Home team gets the cages from 4:45-5:15pm Use batting cage # that corresponds to field number. -

Sabermetrics: the Past, the Present, and the Future
Sabermetrics: The Past, the Present, and the Future Jim Albert February 12, 2010 Abstract This article provides an overview of sabermetrics, the science of learn- ing about baseball through objective evidence. Statistics and baseball have always had a strong kinship, as many famous players are known by their famous statistical accomplishments such as Joe Dimaggio’s 56-game hitting streak and Ted Williams’ .406 batting average in the 1941 baseball season. We give an overview of how one measures performance in batting, pitching, and fielding. In baseball, the traditional measures are batting av- erage, slugging percentage, and on-base percentage, but modern measures such as OPS (on-base percentage plus slugging percentage) are better in predicting the number of runs a team will score in a game. Pitching is a harder aspect of performance to measure, since traditional measures such as winning percentage and earned run average are confounded by the abilities of the pitcher teammates. Modern measures of pitching such as DIPS (defense independent pitching statistics) are helpful in isolating the contributions of a pitcher that do not involve his teammates. It is also challenging to measure the quality of a player’s fielding ability, since the standard measure of fielding, the fielding percentage, is not helpful in understanding the range of a player in moving towards a batted ball. New measures of fielding have been developed that are useful in measuring a player’s fielding range. Major League Baseball is measuring the game in new ways, and sabermetrics is using this new data to find better mea- sures of player performance. -
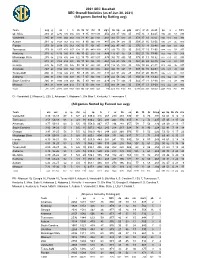
2021 SEC Baseball SEC Overall Statistics (As of Jun 30, 2021) (All Games Sorted by Batting Avg)
2021 SEC Baseball SEC Overall Statistics (as of Jun 30, 2021) (All games Sorted by Batting avg) Team avg g ab r h 2b 3b hr rbi tb slg% bb hp so gdp ob% sf sh sb-att po a e fld% Ole Miss . 2 8 8 67 2278 478 656 109 985 437 1038 . 4 5 6 295 87 570 45 . 3 8 5343 44-65 1759 453 57 . 9 7 5 Vanderbilt . 2 8 5 67 2291 454 653 130 21 92 432 1101 . 4 8 1 301 53 620 41 . 3 7 8 17 33 92-104 1794 510 65 . 9 7 3 Auburn . 2 8 1 52 1828 363 514 101 986 344 891 . 4 8 7 230 34 433 33 . 3 6 8 21 16 32-50 1390 479 45 . 9 7 6 Florida . 2 7 9 59 2019 376 563 105 13 71 351 907 . 4 4 9 262 47 497 32 . 3 7 0 30 4 32-48 1569 528 68 . 9 6 9 Tennessee . 2 7 9 68 2357 475 657 134 12 98 440 1109 . 4 7 1 336 79 573 30 . 3 8 3 27 23 72-90 1844 633 59 . 9 7 7 Kentucky . 2 7 8 52 1740 300 484 86 10 62 270 776 . 4 4 6 176 63 457 28 . 3 6 2 21 16 78-86 1353 436 39 . 9 7 9 Mississippi State . 2 7 8 68 2316 476 644 122 13 75 437 1017 . 4 3 9 306 73 455 50 . 3 7 5 31 13 74-92 1811 515 60 . -

Understanding Advanced Baseball Stats: Hitting
Understanding Advanced Baseball Stats: Hitting “Baseball is like church. Many attend few understand.” ~ Leo Durocher Durocher, a 17-year major league vet and Hall of Fame manager, sums up the game of baseball quite brilliantly in the above quote, and it’s pretty ridiculous how much fans really don’t understand about the game of baseball that they watch so much. This holds especially true when you start talking about baseball stats. Sure, most people can tell you what a home run is and that batting average is important, but once you get past the basic stats, the rest is really uncharted territory for most fans. But fear not! This is your crash course in advanced baseball stats, explained in plain English, so that even the most rudimentary of fans can become knowledgeable in the mysterious world of baseball analytics, or sabermetrics as it is called in the industry. Because there are so many different stats that can be covered, I’m just going to touch on the hitting stats in this article and we can save the pitching ones for another piece. So without further ado – baseball stats! The Slash Line The baseball “slash line” typically looks like three different numbers rounded to the thousandth decimal place that are separated by forward slashes (hence the name). We’ll use Mike Trout‘s 2014 slash line as an example; this is what a typical slash line looks like: .287/.377/.561 The first of those numbers represents batting average. While most fans know about this stat, I’ll touch on it briefly just to make sure that I have all of my bases covered (baseball pun intended). -

The Rules of Scoring
THE RULES OF SCORING 2011 OFFICIAL BASEBALL RULES WITH CHANGES FROM LITTLE LEAGUE BASEBALL’S “WHAT’S THE SCORE” PUBLICATION INTRODUCTION These “Rules of Scoring” are for the use of those managers and coaches who want to score a Juvenile or Minor League game or wish to know how to correctly score a play or a time at bat during a Juvenile or Minor League game. These “Rules of Scoring” address the recording of individual and team actions, runs batted in, base hits and determining their value, stolen bases and caught stealing, sacrifices, put outs and assists, when to charge or not charge a fielder with an error, wild pitches and passed balls, bases on balls and strikeouts, earned runs, and the winning and losing pitcher. Unlike the Official Baseball Rules used by professional baseball and many amateur leagues, the Little League Playing Rules do not address The Rules of Scoring. However, the Little League Rules of Scoring are similar to the scoring rules used in professional baseball found in Rule 10 of the Official Baseball Rules. Consequently, Rule 10 of the Official Baseball Rules is used as the basis for these Rules of Scoring. However, there are differences (e.g., when to charge or not charge a fielder with an error, runs batted in, winning and losing pitcher). These differences are based on Little League Baseball’s “What’s the Score” booklet. Those additional rules and those modified rules from the “What’s the Score” booklet are in italics. The “What’s the Score” booklet assigns the Official Scorer certain duties under Little League Regulation VI concerning pitching limits which have not implemented by the IAB (see Juvenile League Rule 12.08.08). -

FROM BULLDOGS to SUN DEVILS the EARLY YEARS ASU BASEBALL 1907-1958 Year ...Record
THE TRADITION CONTINUES ASUBASEBALL 2005 2005 SUN DEVIL BASEBALL 2 There comes a time in a little boy’s life when baseball is introduced to him. Thus begins the long journey for those meant to play the game at a higher level, for those who love the game so much they strive to be a part of its history. Sun Devil Baseball! NCAA NATIONAL CHAMPIONS: 1965, 1967, 1969, 1977, 1981 2005 SUN DEVIL BASEBALL 3 ASU AND THE GOLDEN SPIKES AWARD > For the past 26 years, USA Baseball has honored the top amateur baseball player in the country with the Golden Spikes Award. (See winners box.) The award is presented each year to the player who exhibits exceptional athletic ability and exemplary sportsmanship. Past winners of this prestigious award include current Major League Baseball stars J. D. Drew, Pat Burrell, Jason Varitek, Jason Jennings and Mark Prior. > Arizona State’s Bob Horner won the inaugural award in 1978 after hitting .412 with 20 doubles and 25 RBI. Oddibe McDowell (1984) and Mike Kelly (1991) also won the award. > Dustin Pedroia was named one of five finalists for the 2004 Golden Spikes Award. He became the seventh all-time final- ist from ASU, including Horner (1978), McDowell (1984), Kelly (1990), Kelly (1991), Paul Lo Duca (1993) and Jacob Cruz (1994). ODDIBE MCDOWELL > With three Golden Spikes winners, ASU ranks tied for first with Florida State and Cal State Fullerton as the schools with the most players to have earned college baseball’s top honor. BOB HORNER GOLDEN SPIKES AWARD WINNERS 2004 Jered Weaver Long Beach State 2003 Rickie Weeks Southern 2002 Khalil Greene Clemson 2001 Mark Prior Southern California 2000 Kip Bouknight South Carolina 1999 Jason Jennings Baylor 1998 Pat Burrell Miami 1997 J.D. -

AB 2.8 Literal Equations.Notebook September 17, 2013
AB 2.8 Literal Equations.notebook September 17, 2013 "Do Now" Classify each number (more than one answer may apply) 1 AB 2.8 Literal Equations.notebook September 17, 2013 Team Hoyt http://www.teamhoyt.com/about/index.html 2 AB 2.8 Literal Equations.notebook September 17, 2013 3 AB 2.8 Literal Equations.notebook September 17, 2013 4 AB 2.8 Literal Equations.notebook September 17, 2013 Unit 2: Solving Equations Name Date 2.8 Literal Equations Block 1. Team Hoyt finished a marathon in d = rt 2 hours and 40 mins (or about 2.6 hours). A marathon is about 26.2 miles. What was their average speed? Use the formula d = rt and round to the nearest tenth. 5 AB 2.8 Literal Equations.notebook September 17, 2013 2. Team Hoyt's average speed during a half- d = rt marathon was about 10.1 miles per hour. A half-marathon is about 13.1 miles. How long did it take them to finish the race? Use the formula d = rt and round to the nearest tenth. 6 AB 2.8 Literal Equations.notebook September 17, 2013 To find a baseball pitcher's 3. earned run average (ERA), you can use the formula Ei = 9r, where E represents ERA, i represents # innings pitched, and r represents # earned runs allowed. Solve the equation for E. What is a pitcher's ERA if he allows 5 earned runs in 18 innings pitched? 7 AB 2.8 Literal Equations.notebook September 17, 2013 On May 14, 1898, a severe 4. -

An Offensive Earned-Run Average for Baseball
OPERATIONS RESEARCH, Vol. 25, No. 5, September-October 1077 An Offensive Earned-Run Average for Baseball THOMAS M. COVER Stanfortl University, Stanford, Californiu CARROLL W. KEILERS Probe fiystenzs, Sunnyvale, California (Received October 1976; accepted March 1977) This paper studies a baseball statistic that plays the role of an offen- sive earned-run average (OERA). The OERA of an individual is simply the number of earned runs per game that he would score if he batted in all nine positions in the line-up. Evaluation can be performed by hand by scoring the sequence of times at bat of a given batter. This statistic has the obvious natural interpretation and tends to evaluate strictly personal rather than team achievement. Some theoretical properties of this statistic are developed, and we give our answer to the question, "Who is the greatest hitter in baseball his- tory?" UPPOSE THAT we are following the history of a certain batter and want some index of his offensive effectiveness. We could, for example, keep track of a running average of the proportion of times he hit safely. This, of course, is the batting average. A more refined estimate ~vouldb e a running average of the total number of bases pcr official time at bat (the slugging average). We might then notice that both averages omit mention of ~valks.P erhaps what is needed is a spectrum of the running average of walks, singles, doublcs, triples, and homcruns per official time at bat. But how are we to convert this six-dimensional variable into a direct comparison of batters? Let us consider another statistic. -

OFFICIAL GAME INFORMATION Lake County Captains (14-15) Vs
High-A Affiliate OFFICIAL GAME INFORMATION Lake County Captains (14-15) vs. Dayton Dragons (16-13) Sunday, June 6th • 1:30 p.m. • Classic Park • Broadcast: WJCU.org Game #30 • Home Game #12 • Season Series: 3-2, 19 Games Remaining RHP Mason Hickman (1-2, 3.45 ERA) vs. RHP Spencer Stockton (2-0, 3.57 ERA) YESTERDAY: The Captains’ three-game winning streak ended with a 15-4 loss to Dayton on Saturday night. Kevin Coulter surrendered seven runs on 10 hits over 1.2 innings to take the loss in a spot start. Dragons centerfielder Quin Cotton hit two home runs and drove in six High-A Central League runs to lead the Dayton offense. Dragons starter Graham Ashcraft earned the win with seven strong innings, in which he allowed just one run on two hits and struck out nine. East Division W L GB COMING ALIVE: After scoring just 12 runs and suffering a six-game sweep last week at West Michigan, the Captains have already scored 29 runs in the first five games of this series against Dayton. Will Brennan has gone 7-for-18 (.389) with two home runs, two doubles, 10 RBI and West Michigan (Detroit) 16 12 -- a 1.254 OPS. Joe Naranjo has gone 3-for-10 with a team-leading five walks for a .533 on-base percentage. Dayton (Cincinnati) 16 13 0.5 BRENNAN BASHING: Captains OF Will Brennan leads the High-A Central League (HAC) lead in doubles (11). He is second in batting average (.326), fourth in wRC+ (154), fifth in on-base percentage (.410), sixth in OPS (.920), sixth in extra-base hits (13) and ninth in slugging Great Lakes (Los Angeles - NL) 15 14 1.5 percentage (.511). -

Lessons You Can Learn by Watching a Game
Lessons You Can Learn by Watching a Game Good coaches no matter how old they are will watch a game and come away learning something. Even if they may be watching the game for enjoyment, there is always something they will see that could possibly help them in the future. A great teaching moment is to take your team to a game or watch a game on TV with them. Show your players during that game not only the good things that are happening but also the things that are done that may cost a run and eventually a game. Coaches can teach their players what to look for during the game like offensive and defensive weaknesses and tendencies. They can teach situations that come up during the game and can teach why something worked or why it didn’t work. Pictures are worth a thousand words. Even watching Major League Baseball games on TV will provide a lot of teachable moments. Lesson One: When Jason Wurth hit the winning walk off home run in the ninth inning during game four against the Cardinals, the Nationals went wild. Yes, it was a big game to win but it was not the Championship game. Watching them storm the field and jump up and down with excitement, made me shake my head. I have been on both sides of that scenario and that becomes bulletin board material. The Cardinals came back to win the next game and take the series. Side note: in case you have never heard that term, bulletin board material means that a player/team said or did something that could make the other team irritated at them to the point that it inspires that other team to do everything possible to beat the team.