DOCSLIB.ORG

20140002716.Pdf

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
20140002716.Pdf Liquid Propulsion Systems – Evolution & Advancements Launch Vehicle Propulsion & Systems LPTC Liquid Propulsion Technical Committee Rick Ballard Liquid Engine Systems Lead SLS Liquid Engines Office NASA / MSFC All rights reserved. No part of this publication may be reproduced, distributed, or transmitted, unless for course participation and to a paid course student, in any form or by any means, or stored in a database or retrieval system, without the prior written permission of AIAA and/or course instructor. Contact the American Institute of Aeronautics and Astronautics, Professional Development Program, Suite 500, 1801 Alexander Bell Drive, Reston, VA 20191-4344 Modules 1. Rocket Propulsion Fundamentals 2. LRE Applications 3. Liquid Propellants 4. Engine Power Cycles 5. Engine Components Module 1: Rocket Propulsion TOPICS Fundamentals • Thrust • Specific Impulse • Mixture Ratio • Isp vs. MR • Density vs. Isp • Propellant Mass vs. Volume Warning: Contents deal with math, • Area Ratio physics and thermodynamics. Be afraid…be very afraid… Terms A Area a Acceleration F Force (thrust) g Gravity constant (32.2 ft/sec2) I Impulse m Mass P Pressure Subscripts t Time a Ambient T Temperature c Chamber e Exit V Velocity o Initial state r Reaction ∆ Delta / Difference s Stagnation sp Specific ε Area Ratio t Throat or Total γ Ratio of specific heats Thrust (1/3) Rocket thrust can be explained using Newton’s 2nd and 3rd laws of motion. 2nd Law: a force applied to a body is equal to the mass of the body and its acceleration in the direction of the force. F ma 3rd Law: For every action, there is an equal and opposite reaction. Fa Fr In rocket propulsion, a mass of propellant (m) is accelerated (via the combustion process) from initial velocity (Vo) to an exit velocity (Ve). The acceleration of this mass is written as: a Ve Vo / t Thrust (2/3) Combining terms, we get: F m(V V ) /t e o Which can be rearranged: m F (Ve Vo ) t The term of mass of propellant divided by time is referred to as mass flow rate (m-dot), expressed as F m (Ve Vo ) Substituting weight flow rate for mass flow rate and assuming a zero initial velocity, the thrust produced by propellant flow (momentum thrust, F1) is shown as m F (V ) 1 g e Thrust (3/3) Another component of thrust (pressure thrust, F2) comes from the force exerted by external pressure differences on the system. This is described by the difference of the pressure of the flow leaving the engine (Pe) through the exit area (Ae) compared to the external (ambient) pressure (Pa). F2 (Pe Pa )Ae In space, Pa is assumed to be zero (which explains why thrust rated at vacuum is higher than at sea level). Combining the two thrust components gives m F (V ) (P P )A g e e a e Specific Impulse (1/4) The total impulse (It) is the thrust integrated over the run duration (time, t) t I Fdt t 0 Assuming constant thrust and negligible transients (i.e., start and shutdown), this becomes I Ft t The specific impulse, (Isp) is the total impulse generated per weight of propellant t Fdt This is really what you need to know about I . F sp I 0 If you want to learn some more, stay seated. sp t m The rest of you can go get some coffee for g mdt about 10 minutes… o 0 Specific Impulse (2/4) Substituting the thrust equation for F gives V A e e Isp (Pe Pa ) g w Under optimal conditions the pressure of the flow exiting the nozzle is equal to that of the C =molar specific heat of exhaust gas ambient pressure (i.e., optimally expanded). pm M = molecular weight of exhaust gas The Isp equation then becomes Ps= isentropic stagnation pressure of the flow at the throat (almost always equivalent Ve to chamber pressure, Pc) I sp g γ= ratio of specific heats of exhaust gas Where the flow exit velocity is calculated by Don’t be intimidated by this 1 – just understand that Ve (and hence I ) is enhanced by sp Pe high release of energy from Ve 2gC pmTc / M 1 the combustion process (high Ps C ) and low molecular pm weight (low M) of the exhaust Specific Impulse (3/4) By definition The equation for Isp then becomes C C 1 p pm 2C pmTc P C C e v vm I sp 1 gM Ps and Cpm Cvm R From this, optimum Isp becomes Where R is the universal 1 gas constant, then 2 RTc Pe Cpm / 1R I spopt 1 1 gM Ps Primarily a function of the Primarily a function of the expansion of combustion process, which is the exhaust gases through the nozzle, influenced by the propellants, which is influenced by back pressure and the mixture ratio and area ratio Specific Impulse (4/4) From an empirical standpoint, determining Isp from test results involves calculating the total impulse generated by the engine and dividing it by the weight of the propellant consumed. t Fdt 0 I sp wconsumed The Isp for flight engines is established (i.e., tagged) on the test stand under simulated flight conditions to ensure acceptance of engine operation and adequate propellant loading of the vehicle. Other primary performance parameters J-2X Acceptance Test Profile (i.e., Thrust, MR) are also tagged during acceptance testing. Mixture Ratio Rocket propellants are mixed in relative quantities to produce the highest possible system Isp. This ratio of propellant consumption is called mixture ratio, MR. w MR o w f In most cases, MR is selected for maximum energy release per weight of propellant. This can be achieved by mixing the propellants in a stoichiometric reaction in the combustion chamber, where all the propellants are thoroughly combusted. However, a stoichiometric MR does not necessarily provide an optimized Isp. The SSME uses a MR of ~6 (stoichiometric for LO2/ LH2 combustion is 8) to reduce the internal and plume temperatures, but also to allow a small amount of H2 to remain in the exhaust. The lighter molecule is able to accelerate to a higher velocity and generate higher kinetic 2 energy (KE = ½ mV ) than a H2O steam exhaust. Isp vs. MR VACIDEAL VACIREAL 480 W inPlot v4.54 460 440 2X - J SSME • “Ideal” for SSME-like fluid 420 2 Vacuum Isp (sec) Isp Vacuum LH conditions (for LO2/LH2 combustion) / 2 and nozzle having ε = 77 used with LO CEA FORTRAN code. 400 • “Real” obtained by accounting for Stoichiometric Stoichiometric typical LO2/LH2 combustion/nozzle efficiencies. 380 1 2 3 4 5 6 7 8 9 10 Mixture Ratio Density vs. Isp . Liquid bipropellant combinations offer a wide . As an example, the densities range of performance capabilities. and Isp performance of the . Each combination has multiple factors that following propellant should be weighed when selecting one for a combinations will be vehicle. compared. • Performance (I ) Density Density sp 3 • Density (higher is better) (g/ml) (lb/ft ) • Storability (venting?) Hydrogen 0.07 4.4 • Ground Ops (hazards?) Methane 0.42 26.4 • Etc. RP-1 0.81 50.6 . One of the more critical trades is that of Oxygen 1.14 71.2 performance versus density. P = 300 psia . LO2/LH2 offers the highest Isp performance, c expanded to MR Isp but at the cost of poor density (thus increasing 14.7 psia (O/F) (sec) tank size). LO /LH 3.5 347(1) . Trading Isp versus density is sometimes 2 2 referred to as comparing “bulk impulse” or LO2/CH4 2.33 263(2) “density impulse”. LO2/RP-1 2.4 263(2) (1) SC (2) FC Propellant Mass vs. Volume 3500000 160000 3000000 140000 ) 3 -24% 120000 2500000 -54% -66% 100000 2000000 80000 1500000 60000 1000000 40000 Total Propellant Volume (ft Volume Propellant Total Total Propellant Mass (lbs) Propellant Total 500000 20000 0 0 1 2 3 LO2/LH1 2 LO2/CH2 4 LO2/RP3 -1 LO2/LH2 LO2/CH4 LO2/RP-1 . For an impulse requirement similar to . When the propellant mass is the 3 SSME’s used on the Shuttle compared against the tank volume, (~1.5 Mlbf for 520 seconds), the there is a significant disparity from required propellant masses are the low hydrogen density that can calculated. adversely impact the size (and total weight) of the vehicle. LO2/LH2 requires 24% less propellant mass than the others. Lesson: Isp isn’t everything – . However… especially with boost stages. Area Ratio (1/2) The parameter that determines exit velocity and pressure of the exhaust gases is area ratio or nozzle expansion ratio, MR A e At • As ε increases, the exit velocity increases and the exit pressure decreases (higher Isp). • When possible, ε is selected so that Pe = Pa and the engine operates at optimum thrust. • For in-space propulsion (i.e., J-2X), the ε is made as large as the weight requirements or volume limitations permit. • If Pe > Pa , then the nozzle is identified as underexpanded and will not provide optimal performance as the plume will continue to expand after exiting the nozzle. • If Pe < Pa , then the nozzle is identified as overexpanded and will not provide optimal performance as the exit shock will migrate inside the nozzle. This can be hazardous from thrust imbalances and damage to the nozzle. Area Ratio (2/2) • Criteria to be considered for selecting a design ε can include the following: • ε provides the optimal integrated performance over the engine operating period. Trajectory analysis is used to determine the altitudes (and Pa) that the engine will operate, which can be used to provide an integrated Isp based on ε.
Load more

Recommended publications
  • Qualification Over Ariane's Lifetime
    r bulletin 94 — may 1998 Qualification Over Ariane’s Lifetime A. González Blázquez Directorate of Launchers, ESA, Paris M. Eymard Groupe Programme CNES/Arianespace, Evry, France Introduction Similarly, the RL10 engine on the Centaur stage The primary objectives of the qualification of the Atlas launcher has been the subject of an activities performed during the operational ongoing improvement programme. About 5000 lifetime of a launcher are: tests were performed before the first flight, and – to verify the qualification status of the vehicle 4000 during the subsequent ten years. – to resolve any technical problems relating to subsystem operations on the ground or in On-going qualification activities of a similar flight. nature were started for the Ariane-3 and 4 launchers in 1986, and for Ariane-5 in 1996. Before focussing on the European family of They can be classified into two main launchers, it is perhaps informative to review categories: ‘regular’ and ‘one-off’. just one or two of the US efforts in the area of solid and liquid propulsion in order to put the Ariane-3/4 accompanying activities Ariane-related activities into context. Regular activities These activities are mainly devoted to In principle, the development programme for a launcher ends with the verification of the qualification status of the qualification phase, after which it enters operational service. In various launcher subsystems. They include the practice, however, the assessment of a launcher’s reliability is a following work packages: continuing process and qualification-type activities proceed, as an – Periodic sampling of engines: one HM7 and extension of the development programme (as is done in aeronautics), one Viking per year, tested to the limits of the over the course of the vehicle’s lifetime.
    [Show full text]
  • High-Thrust In-Space Liquid Propulsion Stage: Storable Propellants
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Institute of Transport Research:Publications Space Propulsion 2014 – ID 2968378 High-Thrust in-Space Liquid Propulsion Stage: Storable Propellants Etienne Dumont, Alexander Kopp, Carina Ludwig, Nicole Garbers DLR, Space Launcher Systems Analysis (SART), Bremen, Germany [email protected] Abstract In the frame of a project funded by ESA, a consortium led Subscripts, Abbreviations by Avio in cooperation with Snecma, Cira, and DLR is ATV Automated Transfer Vehicle performing the preliminary design of a High-Thrust in- CDF Concurrent Design Facility Space Liquid Propulsion Stage for two different types of ECSS European Cooperation on Space manned missions beyond Earth orbit. For these missions, Standardization one or two 100 ton stages are to be used to propel a Elec assy electronic assembly manned vehicle. Three different propellant combinations; EPS Etage à propergols stockables (Ariane 5’s LOx/LH2, LOx/CH4 and MON-3/MMH are being storable propellant stage) compared. GNC Guidance Navigation and Control HTS High-Thrust Stage The preliminary design of the storable variant (MON- IF Interface 3/MMH) has been performed by DLR. The Aestus II ISS International Space Station engine with a large nozzle expansion ratio has been LEO Low Earth Orbit chosen as baseline. A first iteration has demonstrated, that LEOP Launch and Early Orbit Phase it indeed provides the best performance for the storable LH2 Liquid Hydrogen propellant combination, when considering all engines LOx Liquid Oxygen available today or which may be available in a short- to MLI Multi-Layer Insulation medium term.
    [Show full text]
  • Investigation of Condensed and Early Stage Gas Phase Hypergolic Reactions Jacob Daniel Dennis Purdue University
    Purdue University Purdue e-Pubs Open Access Dissertations Theses and Dissertations Fall 2014 Investigation of condensed and early stage gas phase hypergolic reactions Jacob Daniel Dennis Purdue University Follow this and additional works at: https://docs.lib.purdue.edu/open_access_dissertations Part of the Propulsion and Power Commons Recommended Citation Dennis, Jacob Daniel, "Investigation of condensed and early stage gas phase hypergolic reactions" (2014). Open Access Dissertations. 256. https://docs.lib.purdue.edu/open_access_dissertations/256 This document has been made available through Purdue e-Pubs, a service of the Purdue University Libraries. Please contact [email protected] for additional information. i INVESTIGATION OF CONDENSED AND EARLY STAGE GAS PHASE HYPERGOLIC REACTIONS A Dissertation Submitted to the Faculty of Purdue University by Jacob Daniel Dennis In Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy December 2014 Purdue University West Lafayette, Indiana ii To my parents, Jay and Susan Dennis, who have always pushed me to be the person they know I am capable of being. Also to my wife, Claresta Dennis, who not only tolerated me but suffered along with me throughout graduate school. I love you and am so proud of you! iii ACKNOWLEDGEMENTS I would like to express my sincere gratitude to my advisor, Dr. Timothée Pourpoint, for guiding me over the past four years and helping me become the researcher that I am today. In addition I would like to thank the rest of my PhD Committee for the insight and guidance. I would also like to acknowledge the help provided by my fellow graduate students who spent time with me in the lab: Travis Kubal, Yair Solomon, Robb Janesheski, Jordan Forness, Jonathan Chrzanowski, Jared Willits, and Jason Gabl.
    [Show full text]
  • Rocket Propulsion Fundamentals 2
    https://ntrs.nasa.gov/search.jsp?R=20140002716 2019-08-29T14:36:45+00:00Z Liquid Propulsion Systems – Evolution & Advancements Launch Vehicle Propulsion & Systems LPTC Liquid Propulsion Technical Committee Rick Ballard Liquid Engine Systems Lead SLS Liquid Engines Office NASA / MSFC All rights reserved. No part of this publication may be reproduced, distributed, or transmitted, unless for course participation and to a paid course student, in any form or by any means, or stored in a database or retrieval system, without the prior written permission of AIAA and/or course instructor. Contact the American Institute of Aeronautics and Astronautics, Professional Development Program, Suite 500, 1801 Alexander Bell Drive, Reston, VA 20191-4344 Modules 1. Rocket Propulsion Fundamentals 2. LRE Applications 3. Liquid Propellants 4. Engine Power Cycles 5. Engine Components Module 1: Rocket Propulsion TOPICS Fundamentals • Thrust • Specific Impulse • Mixture Ratio • Isp vs. MR • Density vs. Isp • Propellant Mass vs. Volume Warning: Contents deal with math, • Area Ratio physics and thermodynamics. Be afraid…be very afraid… Terms A Area a Acceleration F Force (thrust) g Gravity constant (32.2 ft/sec2) I Impulse m Mass P Pressure Subscripts t Time a Ambient T Temperature c Chamber e Exit V Velocity o Initial state r Reaction ∆ Delta / Difference s Stagnation sp Specific ε Area Ratio t Throat or Total γ Ratio of specific heats Thrust (1/3) Rocket thrust can be explained using Newton’s 2nd and 3rd laws of motion. 2nd Law: a force applied to a body is equal to the mass of the body and its acceleration in the direction of the force.
    [Show full text]
  • Atlas V Cutaway Poster
    ATLAS V Since 2002, Atlas V rockets have delivered vital national security, science and exploration, and commercial missions for customers across the globe including the U.S. Air Force, the National Reconnaissance Oice and NASA. 225 ft The spacecraft is encapsulated in either a 5-m (17.8-ft) or a 4-m (13.8-ft) diameter payload fairing (PLF). The 4-m-diameter PLF is a bisector (two-piece shell) fairing consisting of aluminum skin/stringer construction with vertical split-line longerons. The Atlas V 400 series oers three payload fairing options: the large (LPF, shown at left), the extended (EPF) and the extra extended (XPF). The 5-m PLF is a sandwich composite structure made with a vented aluminum-honeycomb core and graphite-epoxy face sheets. The bisector (two-piece shell) PLF encapsulates both the Centaur upper stage and the spacecraft, which separates using a debris-free pyrotechnic actuating 200 ft system. Payload clearance and vehicle structural stability are enhanced by the all-aluminum forward load reactor (FLR), which centers the PLF around the Centaur upper stage and shares payload shear loading. The Atlas V 500 series oers 1 three payload fairing options: the short (shown at left), medium 18 and long. 1 1 The Centaur upper stage is 3.1 m (10 ft) in diameter and 12.7 m (41.6 ft) long. Its propellant tanks are constructed of pressure-stabilized, corrosion-resistant stainless steel. Centaur is a liquid hydrogen/liquid oxygen-fueled vehicle. It uses a single RL10 engine producing 99.2 kN (22,300 lbf) of thrust.
    [Show full text]
  • Variations of Solid Rocket Motor Preliminary Design for Small TSTO Launcher
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Institute of Transport Research:Publications Space Propulsion 2012 – ID 2394102 Variations of Solid Rocket Motor Preliminary Design for Small TSTO launcher Etienne Dumont Space Launcher Systems Analysis (SART), DLR, Bremen, Germany [email protected] NGL New/Next Generation Launcher Abstract SI Structural Index (mdry / mpropellant) Several combinations of solid rocket motors and ignition SRM Solid Rocket Motor strategies have been considered for a small Two Stage to TSTO Two Stage To Orbit Orbit (TSTO) launch vehicle based on a big solid rocket US Upper Stage motor first stage and cryogenic upper stage propelled by VENUS Vega New Upper Stage the Vinci engine. In order to reach the target payload avg average during the flight performance of about 1400 kg into GTO for the clean s.l. sea level version and 2700 to 3000 kg for the boosted version, the vac vacuum influence of the selected solid rocket motors on the upper 2 + 2 P23 4 P23: two ignited on ground and two with a stage structure has been studied. Preliminary structural delayed ignition designs have been performed and the thrust histories of the solid rocket motor have been tweaked to limit the upper stage structural mass. First stage and booster 1. Introduction combinations with acceptable general loads are proposed. Solid rocket motors (SRM) are commonly used for boosters or launcher first stage. Indeed they can provide high thrust levels while being compact, light and Nomenclature relatively simple compared to a liquid rocket engine Isp specific impulse s providing the same thrust level.
    [Show full text]
  • Argonne Report.Pdf
    CONTENTS NOTATION ........................................................................................................................... xi ABSTRACT ........................................................................................................................... 1 1 INTRODUCTION ........................................................................................................... 5 1.1 Overview of the Emergency Response Guidebook ................................................ 5 1.2 Organization of this Report ..................................................................................... 7 2 GENERAL METHODOLOGY ....................................................................................... 9 2.1 TIH List ................................................................................................................... 10 2.1.1 Background ................................................................................................. 10 2.1.2 Changes in the TIH List for the ERG2012 ................................................. 11 2.2 Shipment and Release Scenarios ............................................................................ 11 2.2.1 Shipment Profiles ........................................................................................ 12 2.2.2 Treatment of Chemical Agents ................................................................... 14 2.3 Generics, Mixtures, and Solutions .......................................................................... 17 2.4 Analysis of Water-Reactive
    [Show full text]
  • Solid Propellant Rocket Engines - V.M
    THERMAL TO MECHANICAL ENERGY CONVERSION: ENGINES AND REQUIREMENTS – Vol. II - Solid Propellant Rocket Engines - V.M. Polyaev and V.A. Burkaltsev SOLID PROPELLANT ROCKET ENGINES V.M. Polyaev and V.A. Burkaltsev Department of Rocket engines, Bauman Moscow State Technical University, Russia. Keywords: Combustion chamber, solid propellant load, pressure, temperature, nozzle, thrust, control, ignition, cartridge, aspect ratio, regime. Contents 1. Introduction 2. Historical information 3. SPRE scheme and main units 4. SPRE operation 5. Parameter optimization, the approach and results 6. Transient regime 7. Service 8. Development prospects 9. Conclusions Acknowledgments Glossary Bibliography Biographical Sketches 1. Introduction Solid propellant rocket engines (SPRE) are called the direct reaction engines, in which chemical energy of the solid propellant being placed in the combustion chamber is transformed at first to thermal energy, and then to kinetic energy of the combustion products thrown away with high velocity in the environment. The momentum of combustion products discharging through the nozzle is equal to the impulse of reactive force being created by the engine. 2. Historical information First of rocketsUNESCO known to us were rockets – with EOLSS primitive powder rocket engines used in China near 5000 years ago for pleasure and military aims (so-called "fiery arrows", Figure 1). SAMPLE CHAPTERS The first rocket propellant was black smoky powder (potassium saltpetre with charcoal mixture). In Russia, powder rockets appeared in the beginning of XVII century. In 1680, Tsar Peter I founded "rocket institution" in Moscow for firework rockets making. In 1717 lighting signal rockets existed for 200 years without changes. In the beginning of XIX century, Englishman Kongrev improved the "fiery arrows" having been borrowed from Hindus.
    [Show full text]
  • Space Almanac 2005
    SpaceAl2005 manac Stratosphere begins 10 miles Limit for turbojet engines 20 miles Limit for ramjet engines 28 miles Astronaut wings awarded 50 miles Low Earth orbit begins 60 miles 0.95G 100 miles Medium Earth orbit begins 300 miles 44 44 AIR FORCEAIR FORCE Magazine Magazine / August / August 2005 2005 SpaceAl manacThe US military space operation in facts and figures. Compiled by Tamar A. Mehuron, Associate Editor, and the staff of Air Force Magazine Hard vacuum 1,000 miles Geosynchronous Earth orbit 22,300 miles 0.05G 60,000 miles NASA photo/staff illustration by Zaur Eylanbekov Illustration not to scale AIR FORCE Magazine / August 2005 AIR FORCE Magazine / /August August 2005 2005 4545 US Military Missions in Space Space Force Support Space Force Enhancement Space Control Space Force Application Launch of satellites and other Provide satellite communica- Assure US access to and freedom Pursue research and devel- high-value payloads into space tions, navigation, weather, mis- of operation in space and deny opment of capabilities for the and operation of those satellites sile warning, and intelligence to enemies the use of space. probable application of combat through a worldwide network of the warfighter. operations in, through, and from ground stations. space to influence the course and outcome of conflict. US Space Funding Millions of constant FY06 dollars $50,000 DOD 45,000 NASA 40,000 Other Total 35,000 30,000 25,000 20,000 15,000 10,000 5,000 0 59 62 66 70 74 78 82 86 90 94 98 02 04 Fiscal Year FY NASA DOD Other Total FY NASA DOD Other
    [Show full text]
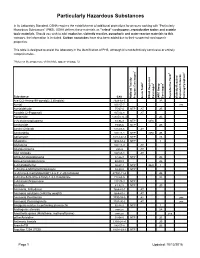
  • Particularly Hazardous Substances
    Particularly Hazardous Substances In its Laboratory Standard, OSHA requires the establishment of additional protections for persons working with "Particularly Hazardous Substances" (PHS). OSHA defines these materials as "select" carcinogens, reproductive toxins and acutely toxic materials. Should you wish to add: explosive, violently reactive, pyrophoric and water-reactve materials to this category, the information is included. Carbon nanotubes have also been added due to their suspected carcinogenic properties. This table is designed to assist the laboratory in the identification of PHS, although it is not definitively conclusive or entirely comprehensive. *Notes on the proper use of this table appear on page 12. 1 6 5 2 3 4 Substance CAS National Toxicity National Program Carcinogen Toxin Acute Regulated OSHA Carcinogen Group IARC Carcinogen Toxin Reproductive Violently Reactive/ Explosive/Peroxide Forming/Pyrophoric A-a-C(2-Amino-9H-pyrido[2,3,b]indole) 2648-68-5 2B Acetal 105-57-7 yes Acetaldehyde 75-07-0 NTP AT 2B Acrolein (2-Propenal) 107-02-8 AT Acetamide 126850-14-4 2B 2-Acetylaminofluorene 53-96-3 NTP ORC Acrylamide 79-06-6 NTP 2B Acrylyl Chloride 814-68-6 AT Acrylonitrile 107-13-1 NTP ORC 2B Adriamycin 23214-92-8 NTP 2A Aflatoxins 1402-68-2 NTP 1 Allylamine 107-11-9 AT Alkylaluminums varies AT Allyl Chloride 107-05-1 AT ortho-Aminoazotoluene 97-56-3 NTP 2B para-aminoazobenzene 60-09-3 2B 4-Aminobiphenyl 92-67-1 NTP ORC 1 1-Amino-2-Methylanthraquinone 82-28-0 NTP (2-Amino-6-methyldipyrido[1,2-a:3’,2’-d]imidazole) 67730-11-4 2B
    [Show full text]
  • Ghs Reference Materials Health Hazard Criteria
    APPENDIX F: GHS REFERENCE MATERIALS This appendix provides both an overview of GHS highly toxic hazard classification. A listing of Particularly Hazardous Substances that Carnegie Mellon University has published with their Chemical Hygiene plan is also provided as general reference. The list is useful cross check with GHS listings to determine which materials require prior approval for use BUT NO LIST IS COMPLETE you must check the SDS for possible additional chemicals rated as highly toxic. This appendix also provides the GHS (global harmonization system) for chemical hazard classification under the Hazard Communication Standard for highly toxic materials. This section provides overall information about categories under the classification of acute toxicity, mutagens’, reproductive and carcinogen hazards. When chemicals are rated on the GHS – Safety Data Sheet (SDS) as the following hazards then the PRIOR APPROVAL PROCESS WITH CHEMICAL HYGIENE OFFICER/COMMITTEE must be used: Acute toxicity category 1 and 2, Germ cell mutagenicity as a category 1A Substances known to induce heritable mutations in germ cells of humans and Category 1B: Substances which should be regarded as if they induce heritable mutations in the germ cells of humans, Reproductive Hazard as a category 1: Known or presumed human reproductive toxicants and Category 2; suspected human reproductive toxicant. Carcinogen as a Category 1 (includes 1A and 1B): Known or presumed human carcinogens, Category 2: Suspected human carcinogens. The Campus Chemical Hygiene Committee (Officer) must conduct a prior approval process. Appendix C Chemical Prior Approval Form on procedure for conducing prior approval. The following is from OSHA standard on the chemicals classifications that PCC Laboratory instructional operations shall use for defining the prior approval hazards.
    [Show full text]
  • A Tool for Preliminary Design of Rockets Aerospace Engineering
    A Tool for Preliminary Design of Rockets Diogo Marques Gaspar Thesis to obtain the Master of Science Degree in Aerospace Engineering Supervisor : Professor Paulo Jorge Soares Gil Examination Committee Chairperson: Professor Fernando José Parracho Lau Supervisor: Professor Paulo Jorge Soares Gil Members of the Committee: Professor João Manuel Gonçalves de Sousa Oliveira July 2014 ii Dedicated to my Mother iii iv Acknowledgments To my supervisor Professor Paulo Gil for the opportunity to work on this interesting subject and for all his support and patience. To my family, in particular to my parents and brothers for all the support and affection since ever. To my friends: from IST for all the companionship in all this years and from Coimbra for the fellowship since I remember. To my teammates for all the victories and good moments. v vi Resumo A unica´ forma que a humanidade ate´ agora conseguiu encontrar para explorar o espac¸o e´ atraves´ do uso de rockets, vulgarmente conhecidos como foguetoes,˜ responsaveis´ por transportar cargas da Terra para o Espac¸o. O principal objectivo no design de rockets e´ diminuir o peso na descolagem e maximizar o payload ratio i.e. aumentar a capacidade de carga util´ ao seu alcance. A latitude e o local de lanc¸amento, a orbita´ desejada, as caracter´ısticas de propulsao˜ e estruturais sao˜ constrangimentos ao projecto do foguetao.˜ As trajectorias´ dos foguetoes˜ estao˜ permanentemente a ser optimizadas, devido a necessidade de aumento da carga util´ transportada e reduc¸ao˜ do combust´ıvel consumido. E´ um processo utilizado nas fases iniciais do design de uma missao,˜ que afecta partes cruciais do planeamento, desde a concepc¸ao˜ do ve´ıculo ate´ aos seus objectivos globais.
    [Show full text]