Madhya Bharti 75 21.07.18 English
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Epic Imagination in Contemporary Indian Literature
University of South Florida Scholar Commons Graduate Theses and Dissertations Graduate School May 2017 Modern Mythologies: The picE Imagination in Contemporary Indian Literature Sucheta Kanjilal University of South Florida, [email protected] Follow this and additional works at: http://scholarcommons.usf.edu/etd Part of the South and Southeast Asian Languages and Societies Commons Scholar Commons Citation Kanjilal, Sucheta, "Modern Mythologies: The pE ic Imagination in Contemporary Indian Literature" (2017). Graduate Theses and Dissertations. http://scholarcommons.usf.edu/etd/6875 This Dissertation is brought to you for free and open access by the Graduate School at Scholar Commons. It has been accepted for inclusion in Graduate Theses and Dissertations by an authorized administrator of Scholar Commons. For more information, please contact [email protected]. Modern Mythologies: The Epic Imagination in Contemporary Indian Literature by Sucheta Kanjilal A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy with a concentration in Literature Department of English College of Arts and Sciences University of South Florida Major Professor: Gurleen Grewal, Ph.D. Gil Ben-Herut, Ph.D. Hunt Hawkins, Ph.D. Quynh Nhu Le, Ph.D. Date of Approval: May 4, 2017 Keywords: South Asian Literature, Epic, Gender, Hinduism Copyright © 2017, Sucheta Kanjilal DEDICATION To my mother: for pencils, erasers, and courage. ACKNOWLEDGEMENTS When I was growing up in New Delhi, India in the late 1980s and the early 1990s, my father was writing an English language rock-opera based on the Mahabharata called Jaya, which would be staged in 1997. An upper-middle-class Bengali Brahmin with an English-language based education, my father was as influenced by the mythological tales narrated to him by his grandmother as he was by the musicals of Broadway impressario Andrew Lloyd Webber. -

Issn 2319 – 9202
INTERNATIONAL RESEARCH JOURNAL OF COMMERCE, ARTS AND SCIENCE ISSN 2319 – 9202 An Internationally Indexed Peer Reviewed & Refereed Journal Shri Param Hans Education & Research Foundation Trust WWW.CASIRJ.COM www.SPHERT.org Published by iSaRa Solutions CASIRJ Volume 10 Issue 8 [Year - 2019] ISSN 2319 – 9202 ROLE OF JAMBUBATI PATTANAIK IN THE FREEDOM MOVEMENT OF WESTERN ODISHA Ms. Minatee Debata Lect. in History Jamla Degree College, Jamla Via- Padampur- 768049 District- Bargarh, Odisha The Western part of Odisha, extending from the Kalahandi District in the south to the Sundergarh District in the North West, which comprised of the present districts of Balangir, Bargarh, Boudh, Deogarh, Jharsuguda, Kalahandi, Nuapada, Sambalpur, Sonepur, Sundargarh and Athmallik sdivision of Angul District has a great contribution to the Indian struggle for Independence. In Western Odisha women played a vital role in the freedom movement. The notable women leaders who stand in the fore front during the national movement were Jambobati Devi (wife of famous freedom fighter Bhagirathi Pattanaik), Prabhabati Devi (daughter of Dhanpati Dash of Bargarh), Parvati Giri (The Mother Teresa of Western Odisha), Gurubari Meher (a valiant women freedom fighter of Sonepur), Saraswati Mirdha, Rukmini devi Lath (the wife of Sri Prahallad Rai Lath of Sambalpur), Gandharvi Devi (daughter-in-law of Fakira Behera), Iia Meher (the wife of Kunja Bihari of Tukurla), Shreeyabati Devi (wife of senior freedom fighter Ghanashyam Panigrahi of Manpur, Bhaden) and many more. These women freedom fighters of western Odisha made momentous contribution to the freedom struggle by demonstrating their indomitable courage and unflinching patriotism. One of the most prominent among these freedom fighters of western odisha was Jambubati Devi. -

Abhinavagupta's Portrait of a Guru: Revelation and Religious Authority in Kashmir
Abhinavagupta's Portrait of a Guru: Revelation and Religious Authority in Kashmir The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters Citable link http://nrs.harvard.edu/urn-3:HUL.InstRepos:39987948 Terms of Use This article was downloaded from Harvard University’s DASH repository, and is made available under the terms and conditions applicable to Other Posted Material, as set forth at http:// nrs.harvard.edu/urn-3:HUL.InstRepos:dash.current.terms-of- use#LAA Abhinavagupta’s Portrait of a Guru: Revelation and Religious Authority in Kashmir A dissertation presented by Benjamin Luke Williams to The Department of South Asian Studies in partial fulfillment of the requirements for the degree of Doctor of Philosophy in the subject of South Asian Studies Harvard University Cambridge, Massachusetts August 2017 © 2017 Benjamin Luke Williams All rights reserved. Dissertation Advisor: Parimal G. Patil Benjamin Luke Williams ABHINAVAGUPTA’S PORTRAIT OF GURU: REVELATION AND RELIGIOUS AUTHORITY IN KASHMIR ABSTRACT This dissertation aims to recover a model of religious authority that placed great importance upon individual gurus who were seen to be indispensable to the process of revelation. This person-centered style of religious authority is implicit in the teachings and identity of the scriptural sources of the Kulam!rga, a complex of traditions that developed out of more esoteric branches of tantric "aivism. For convenience sake, we name this model of religious authority a “Kaula idiom.” The Kaula idiom is contrasted with a highly influential notion of revelation as eternal and authorless, advanced by orthodox interpreters of the Veda, and other Indian traditions that invested the words of sages and seers with great authority. -

Tourism Department VARANASI CENTRE in Partial Fulfillment of The
Tourism Department VARANASI CENTRE In Partial fulfillment of the Requirement for the award of “Bachelor Degree in Tourism 2011-012 Submitted To :- Submitted By :- A.K Singh Nilesh Kumar Chaurasia Project executed at At Varanasi, Uttar Pradesh Under the guidance of DR. AK. Singh Indira Gandhi National Open University ACKNOWLEDGEMENT First of all I would thank to Almighty God and my parents for their precious support and help towards this project. I deem it a privilege and pleasure in submitting this project “” in Indore. It was indeed a great feeling to do my project ,and I would like to specially thank my Project Guide Dr.A.K.SINGH for guiding me at every step and making this project a learning opportunity. I would also like to let others know my sense of indebtedness towards ………. for giving me an opportunity to undertake this project DECLARATION I hereby declare that this project entitled –“” in Varanasi, Submitted to Indira Gandhi National Open University in partial fulfillment of the requirements of the award of the degree Bachelor in Tourism is a record of original research work done by me under the supervision and guidance of Professor A.K.SINGH faculty Guide, It is also hereby stated that this has not formed the basis of or the award of any degree or any fellowship or any other similar title to any scholar in any university. Date:- FEB/ 23/2011 Place:- Varanasi Name:- Nilesh Kumar Chaurasia CONTENT List of Content Page No Introduction 6 Resources Of Marketing In Varanasi 7 Study Of Title 18 CHAPTER –I :- Problem Formulation 19 i) -

Mumbai Macbeth: Gender and Identity in Bollywood Adaptations Rashmila Maiti University of Arkansas, Fayetteville
University of Arkansas, Fayetteville ScholarWorks@UARK Theses and Dissertations 8-2018 Mumbai Macbeth: Gender and Identity in Bollywood Adaptations Rashmila Maiti University of Arkansas, Fayetteville Follow this and additional works at: http://scholarworks.uark.edu/etd Part of the Asian Studies Commons, Comparative Literature Commons, and the Literature in English, British Isles Commons Recommended Citation Maiti, Rashmila, "Mumbai Macbeth: Gender and Identity in Bollywood Adaptations" (2018). Theses and Dissertations. 2905. http://scholarworks.uark.edu/etd/2905 This Dissertation is brought to you for free and open access by ScholarWorks@UARK. It has been accepted for inclusion in Theses and Dissertations by an authorized administrator of ScholarWorks@UARK. For more information, please contact [email protected], [email protected]. Mumbai Macbeth: Gender and Identity in Bollywood Adaptations A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Comparative Literature and Cultural Studies by Rashmila Maiti Jadavpur University Bachelor of Arts in English Literature, 2007 Jadavpur University Master of Arts in English Literature, 2009 August 2018 University of Arkansas This dissertation is approved for recommendation to the Graduate Council. M. Keith Booker, PhD Dissertation Director Yajaira M. Padilla, PhD Frank Scheide, PhD Committee Member Committee Member Abstract This project analyzes adaptation in the Hindi film industry and how the concepts of gender and identity have changed from the original text to the contemporary adaptation. The original texts include religious epics, Shakespeare’s plays, Bengali novels which were written pre- independence, and Hollywood films. This venture uses adaptation theory as well as postmodernist and postcolonial theories to examine how women and men are represented in the adaptations as well as how contemporary audience expectations help to create the identity of the characters in the films. -

Revised Syllabus for P.G. Courses in Philosophy
REVISED SYLLABUS FOR P.G. COURSES IN PHILOSOPHY COURSE NO. PHIL/P.G/1.1 Logic (Indian) 1. Nature of Indian Logic: the close relationship of logic, epistemology and metaphysics in the Indian tradition; primacy of logical reasoning in establishing one’ own system and refuting all rival systems; the concepts of ānvikṣikī and anumiti 2. Definition of Anumāna: Nyāya and Buddhist perspectives 3. Constituents of Anumāna: Nyāya and Buddhist perspectives 4. Process of Anumāna: Nyāya and Buddhist perspectives 5. Types of Anumāna: Nyāya and Buddhist perspectives 6. Nyāya: paķṣata, parāmarśa, definition of vyāpti 7. Inductive elements in Indian Logic: the concepts of vyāptigrahopāya, sāmānyalakṣaṇaprātyasatti, tarka, upādhi 8. Hetvābhāsa 9. Jňāniyapratibaddha-pratibandhakābhāva Suggestive Texts: Keśava Miśra: Tarkabhāṣā, ed. by Pandit Badarinath Shukla, Motilal Banarasidas Publishers Ltd., N. Delhi Dharmakīrti: Nyāyabindu, ed. by D. Malvania, Patna, 1971 Uddyotakara: Nyāyavārttika, ed. by M. M. Anantalal Thakur, ICPR Publication, N. Delhi Praśastapādabhāṣya, ed. By Ganganath Jha, Sapurnanda Sanskrit University, Benares Nyāyasūtra – Vātsayanabhāsya (select portions), ed. by MM Phanibhusan Tarkavagish, Rajya Pustak Parshad, WB Viśvanātha,Bhāṣāparichheda, ed. by Pandit Panchanan Shastri with commentary Muktavali- Samgraha, Sanskrita Pustak Bhandar Annambhatta,TarkasaṁgrahawithDipika, ed. by Pandit Panchanan Shastri, Sanskrita Pustak Bhandar (Bengali) Annambhatta,TarkasaṁgrahawithDipika, trans. by Prof. Gopinath Bhattacharya in English, Progressive Pub, 1976 Suggested Readings: S.S. Barlingay,A Modern Introduction to Indian Logic, National Publishing House, 1965 Gangadhar Kar,Tarkabhāsā Vol– I, 2nd ed. Jadavpur University Press, 2009 19 D.C. Guha,Navya Nyaya System of Logic, Motilal Banarsidass, 1979 Nandita Bandyopadhyay,The Concept of Logical Fallacies, Sanskrit Pustak Bhandar, 1977 B.K. Matilal,The Navya Nyaya Doctrine of Negation,Harvard University Press, 1968 B.K. -

Ananda Varta Index I
ĀNANDA VĀRTĀ CONTENTS VOLUME I ENGLISH SECTION 1. Mother’s Words .. 19, 47, 121, 193, 293 2. Mataji’s Amara Vani .. 124, 296 3. An Appeal—Gurupriya Devi .. 1 4. Shree Shree Ma Anandamayee—A brief account of Her movements since March, 1951—Gurupriya Devi .. 3 5. An Incident—Ranjan .. 10 6. Durga Puja at Banaras—Ranjan .. 13 7. Samyam Vrata—Atmananda .. 50 8. Ma Anandamayee in Madras and Tiruvannamalai —S.S Cohen (Sri Ramanashram) .. 54 9. Our Goal—a well-wisher .. 64 10. A Unique Personality—Akshay Kumar Daila Gupta .. 129 11. The Miracle at Bindhyachal—Ranjan .. 132 12. Mother Plays Holi at Brindaban—a Devotee .. 134 13. “Didima”—Atmananda .. 136 14. Mother: A Symbol of Higher Life for Man — Gangacharan Das Gupta .. 138, 198 15. Mother Anandamayee—Dr. Nalini Kanta Brahma .. 144 16. Mother and the World Situation — Akshay Kumar Daila Gupta .. 196 17. A Request to Devotees—Rajmata Anandapriya ..205 18. Shri Anandamayi—The Mother — Acharya Srimad Gopal Chandra Chattopadhyaya .. 302 19. I Wonder—Ranjan .. 307 20. Notes and Comments .. 23, 65, 146, 312 ĀNANDA VĀRTĀ CONTENTS VOLUME II ENGLISH SECTION 1. Matri Vani .. 63, 161, 255, 360 2. Mataji’s Amara Vani .. 66, 165, 259, 363 3. Greetins From A European .. 77 4. Guru-Sanga—S. S. Cohen .. 82 5. Mother’s Divine Grace—Ganga Charan Das Gupta .. 85 6. The Supreme Teacher I found in Sri Sri Ma Anandamayi—Atmananda .. 89 7. Birthday Celebrations at Almora—Kali Prasad .. 171 8. At Mataji’s Camp on the Day of the Kumbh Disaster —A Devotee .. 177 9. -

List of Documentary Films Produced by Sahitya Akademi
Films Produced by Sahitya Akademi (Till Date) S.No. Author Directed by Duration 1. Amrita Pritam (Punjabi) Basu Bhattacharya 60 minutes 2. Akhtar-ul-Iman (Urdu) Saeed Mirza 60 minutes 3. V.K. Gokak (Kannada) Prasanna 60 minutes 4. Takazhi Sivasankara Pillai (Malayalam) M.T. Vasudevan Nair 60 minutes 5. Gopalkrishna Adiga (Kannada) Girish Karnad 60 minutes 6. Vishnu Prabhakar (Hindi) Padma Sachdev 60 minutes 7. Balamani Amma (Malayalam) Madhusudanan 27 minutes 8. Vinda Karandikar (Marathi) Nandan Kudhyadi 60 minutes 9. Annada Sankar Ray (Bengali) Budhadev Dasgupta 60 minutes 10. P.T. Narasimhachar (Kannada) Chandrasekhar Kambar 27 minutes 11. Baba Nagarjun (Hindi) Deepak Roy 27 minutes 12. Dharamvir Bharti (Hindi) Uday Prakash 27 minutes 13. D. Jayakanthan (Tamil) Sa. Kandasamy 27 minutes 14. Narayan Surve (Marathi) Dilip Chitre 27 minutes 15. Bhisham Sahni (Hindi) Nandan Kudhyadi 27 minutes 16. Subhash Mukhopadhyay (Bengali) Raja Sen 27 minutes 17. Tarashankar Bandhopadhyay (Bengali) Amiya Chattopadhyay 27 minutes 18. Vijaydan Detha (Rajasthani) Uday Prakash 27 minutes 19. Navakanta Barua (Assamese) Gautam Bora 27 minutes 20. Mulk Raj Anand (English) Suresh Kohli 27 minutes 21. Gopal Chhotray (Oriya) Jugal Debata 27 minutes 22. Qurratulain Hyder (Urdu) Mazhar Q. Kamran 27 minutes 23. U.R. Anantha Murthy (Kannada) Krishna Masadi 27 minutes 24. V.M. Basheer (Malayalam) M.A. Rahman 27 minutes 25. Rajendra Shah (Gujarati) Paresh Naik 27 minutes 26. Ale Ahmed Suroor (Urdu) Anwar Jamal 27 minutes 1 27. Trilochan Shastri (Hindi) Satya Prakash 27 minutes 28. Rehman Rahi (Kashmiri) M.K. Raina 27 minutes 29. Subramaniam Bharati (Tamil) Soudhamini 27 minutes 30. O.V. -

ON DADAJI PART I Second Edition Published by Sri A.N
ON DADAJI PART I Second Edition Published by Sri A.N. Sain on behalf of ‘Anami’ (online distribution only) Cover by Prof. Ratindra Nath Maitra – Govt. College of Arts, Secty, Academy October 2006 of Fine Arts Amida Press First Edition: March 1971 POB 801 Printed by: Bibbas Kumar Guha Thakurta La Center WA Byabosa-O-Banijya Press 98629 USA 9/3, Ramanath Majumdar Street, Calcutta – 9 PUBLISHER’S NOTE Email: Dadaji, the saint and savant of the present century, has revealed himself to [email protected] show people the real path of Truth which will qualify them for initiation into higher life. Articles of this book confirm that life cannot be divorced – Websites: from ethical background nor dissociated from spiritual urge; otherwise life www.dadaji.info becomes a mere aimless and rootless existence. According to Dadaji, no www.dadaji.us penance is required for spiritual salvation’ only by selfless love and the aspiration for truth we can reach the ultimate goal of life. --- February 16, 1971 - A.N. Sain, on behalf of ANIMI CONTENTS Page PDF file Introduction – An Unknown Mystic iii On.Dadaji.Vol.I.Intro.pdf 1. Views and Values about Bhibuti of Dadaji - Amit Anirban 1 On.Dadaji.Vol.I.1.pdf 2. Sradh and Satyanarayan – Professor Bibhuti Sarkar 3 3. How I Came to Know Dadaji – Dr S. Bose 11 On.Dadaji.Vol.I.2.pdf 4. Sri Dadaji – Dr M.N. Shukla 14 5. Know Your Dada – Sri Sachin Roy Chowdhury 16 6. Days of Miracles are Not Over – Dr Manas Maitra 19 On.Dadaji.Vol.I.3.pdf 7. -

Strategies Xxi the Complex and Dynamic Nature of The
“CAROL I” NATIONAL DEFENCE UNIVERSITY Centre for Defence and Security Strategic Studies THE INTERNATIONAL SCIENTIFIC CONFERENCE STRATEGIES XXI With the theme: THE COMPLEX AND DYNAMIC NATURE OF THE SECURITY ENVIRONMENT NOVEMBER 22-23, 2012, BUCHAREST Coordinators: Alexandra SARCINSCHI, PhD Cristina BOGZEANU “CAROL I” NATIONAL DEFENCE UNIVERSITY PUBLISHINGHOUSE BUCHAREST, 2012 SCIENTIFIC COMMITTEE - Teodor FRUNZETI, PhD. prof., “Carol I” National Defence University, Romania - Ion ROCEANU, PhD. prof., “Carol I” National Defence University, Romania - Petre DUŢU, senior researcher PhD., “Carol I” National Defence University, Romania - Bogdan AURESCU, PhD. lecturer, University of Bucharest, Romania - Silviu NEGUŢ, PhD. prof., Bucharest Academy of Economic Studies, Romania - Rudolf URBAN, PhD. prof., Defence University, Czech Republic - Pavel NECAS, PhD. prof. dipl. eng., Armed Forces Academy, Slovakia - Alexandra SARCINSCHI, senior researcher PhD., “Carol I” National Defence University, Romania - Cristian BĂHNĂREANU, senior researcher PhD., “Carol I” National Defence University, Romania - Mihai-Ştefan DINU, senior researcher PhD., “Carol I” National Defence University, Romania - Cristina BOGZEANU, junior researcher, “Carol I” National Defence University, Romania ADMINISTRATIVE COMMITTEE - Petre DUŢU senior researcher PhD. - Irina TĂTARU, PhD. - Mirela ATANASIU, PhD. - George RĂDUICĂ, PhD. - Daniela RĂPAN - Doina MIHAI - Marioara PETRE-BĂJENARU COPYRIGHT: Any reproduction is authorized, without fees, provided that the source is mentioned. • -

Draft District Survey Report (Dsr) of Jagatsinghpur District, Odisha for River Sand
DRAFT DISTRICT SURVEY REPORT (DSR) OF JAGATSINGHPUR DISTRICT, ODISHA FOR RIVER SAND (FOR PLANNING & EXPLOITING OF MINOR MINERAL RESOURCES) ODISHA As per Notification No. S.O. 3611(E) New Delhi, 25th July, 2018 MINISTRY OF ENVIRONMENT, FOREST AND CLIMATE CHANGE (MoEF & CC) COLLECTORATE, JAGATSINGHPUR CONTENT SL NO DESCRIPTION PAGE NO 1 INTRODUCTION 1 2 OVERVIEW OF MINING ACTIVITIES IN THE DISTRICT 2 3 LIST OF LEASES WITH LOCATION, AREA AND PERIOD OF 2 VALIDITY 4 DETAILS OF ROYALTY COLLECTED 2 5 DETAILS OF PRODUCTION OF SAND 3 6 PROCESS OF DEPOSIT OF SEDIMENTS IN THE RIVERS 3 7 GENERAL PROFILE 4 8 LAND UTILISATION PATTERN 5 9 PHYSIOGRAPHY 6 10 RAINFALL 6 11 GEOLOGY AND MINERAL WALTH 7 LIST OF PLATES DESCRIPTION PLATE NO INDEX MAP OF THE DISTRICT 1 MAP SHOWING TAHASILS 2 ROAD MAP OF THE DISTRICT 3 MINERAL MAP OF THE DISTRICT 4 LEASE/POTENTIAL AREA MAP OF THE DISTRICT 5 1 | Page PLATE NO- 1 INDEX MAP ODISHA PLATE NO- 2 MAP SHOWING THE TAHASILS OF JAGATSINGHPUR DISTRICT Cul ••• k L-. , •....~ .-.-.. ••... --. \~f ..•., lGte»d..) ( --,'-....• ~) (v~-~.... Bay of ( H'e:ngal 1< it B.., , . PLATE NO- 3 MAP SHOWING THE MAJOR ROADS OF JAGATSINGHPUR DISTRICT \... JAGADSINGHPU R KENDRAPARA \1\ DISTRICT ~ -,---. ----- ••.• "'1. ~ "<, --..... --...... --_ .. ----_ .... ---~.•.....•:-. "''"'\. W~~~~~·~ ~~~~;:;;:2---/=----- ...------...--, ~~-- . ,, , ~.....••.... ,. -'.__J-"'" L[GEND , = Majar Roaod /""r •.•.- •.... ~....-·i Railway -- ------ DisAJict '&IWldEIIY PURl - --- stale Baumlallji' River Map noI to Sl::a-,~ @ D~triGlHQ CopyTig:hI@2012w_mapso,fin.dia_oo:m • OlllerTi:nim (Updated on 17th iNll~el'llber 2012) MajorTcown PREFACE In compliance to the notification issued by the Ministry of Environment and Forest and Climate Change Notification no. -
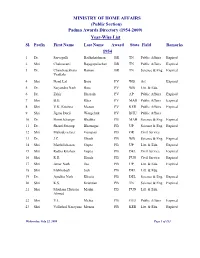
(Public Section) Padma Awards Directory (1954-2009) Year-Wise List Sl
MINISTRY OF HOME AFFAIRS (Public Section) Padma Awards Directory (1954-2009) Year-Wise List Sl. Prefix First Name Last Name Award State Field Remarks 1954 1 Dr. Sarvapalli Radhakrishnan BR TN Public Affairs Expired 2 Shri Chakravarti Rajagopalachari BR TN Public Affairs Expired 3 Dr. Chandrasekhara Raman BR TN Science & Eng. Expired Venkata 4 Shri Nand Lal Bose PV WB Art Expired 5 Dr. Satyendra Nath Bose PV WB Litt. & Edu. 6 Dr. Zakir Hussain PV AP Public Affairs Expired 7 Shri B.G. Kher PV MAH Public Affairs Expired 8 Shri V.K. Krishna Menon PV KER Public Affairs Expired 9 Shri Jigme Dorji Wangchuk PV BHU Public Affairs 10 Dr. Homi Jehangir Bhabha PB MAH Science & Eng. Expired 11 Dr. Shanti Swarup Bhatnagar PB UP Science & Eng. Expired 12 Shri Mahadeva Iyer Ganapati PB OR Civil Service 13 Dr. J.C. Ghosh PB WB Science & Eng. Expired 14 Shri Maithilisharan Gupta PB UP Litt. & Edu. Expired 15 Shri Radha Krishan Gupta PB DEL Civil Service Expired 16 Shri R.R. Handa PB PUN Civil Service Expired 17 Shri Amar Nath Jha PB UP Litt. & Edu. Expired 18 Shri Malihabadi Josh PB DEL Litt. & Edu. 19 Dr. Ajudhia Nath Khosla PB DEL Science & Eng. Expired 20 Shri K.S. Krishnan PB TN Science & Eng. Expired 21 Shri Moulana Hussain Madni PB PUN Litt. & Edu. Ahmed 22 Shri V.L. Mehta PB GUJ Public Affairs Expired 23 Shri Vallathol Narayana Menon PB KER Litt. & Edu. Expired Wednesday, July 22, 2009 Page 1 of 133 Sl. Prefix First Name Last Name Award State Field Remarks 24 Dr.