DOCSLIB.ORG

To Start Data Analysis You Must Log Into

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
To Start Data Analysis You Must Log Into Overview Your task is to use Spitzer Space Telescope observations to determine how much infrared energy is being emitted from the center of certain galaxies. You will use images of galaxies in 4 different wavelengths from the Infrared Array Camera (IRAC); 3.6, 4.5, 5.8 and 8.0 microns. The galaxies we have targeted are called Active Galactic Nuclei, or AGN. They are called "active" because they emit large amounts of energy at many wavelengths above and beyond what we would calculate based on the total numbers of stars at their center. We believe the excess energy is generated by material flowing into a huge black hole at their centers. Your measurements of the infrared emission from these objects will be combined with your (or other students’) measurements of the radio emission from these same objects, as well as estimates made by professional astronomers of the masses of the black holes at their centers. We hope that we will learn more about how AGNs work by determining if and how their infrared and radio emissions depend on the mass of the black hole. To determine the infrared energy emitted from the surrounding region of the black hole, you will do these things: 1) Log onto a Lewis Center computer, and run two computer programs (called IDL and ATV) that are used for visualizing and manipulating data. 2) Load your Spitzer data into ATV and adjust the image of the AGN so you can more easily see it. 3) Determine how much energy was received from the center of the AGN. This is a two step process. First, you measure how much total energy is coming from the central region. Second, you must subtract off any background emission that is present. (This background is emission from many other things that are in the area, in addition to the nucleus of the galaxy.) As you will see, the ATV program is set-up to make this very easy for you to do! 4) Answer some questions about what you have learned and relate them to your radio work. At the end of this document we list the masses of the black holes you have observed. You will use this information in the analysis of the data. 1. Start the Data Analysis Software To start data analysis you must log into: http://idl2.gavrt.org/ You will get a page with a password requirement. The password is: g4vrt4u Then you will get the following screen that may also require a password. Put in the same password. You will have an image of another desktop. On that desktop is an icon called “IDL.” Double click on it to open This will start two screens, one is running a program called IDL: and the other has a program called ATV which is generated by IDL. It is the tool you will use to display and analyze the data from the Spitzer Space Telescope. Right now it should be displaying a cross, which is the default image: IMPORTANT NOTE: At times the cursor can leave a trail that can cover the text (see figure on left). If you need to refresh the screen DO NOT use the “Page Reload” option of the browser (the one with the circular arrow on top)!!! Either use the “Refresh” button at the top center, or minimize and then maximize the screen. If you use the “Page Reload” button you will be taken to the login screen again, though your work will not be destroyed. 2. Loading Your Data and Adjusting the Image Spitzer files are saved in FITS format which is the most common format that astronomical images are saved. It stands for Flexible Image Transport System. Go to the “File” menu and open the image that you wish to analyze using “Readfits.” These images should have been uploaded to the Lewis Center and placed in a directory where you should be able to open them. If the images you are looking for do not show up when you use the “Readfits” function, contact the Lewis Center. As an example you can load in the image n4945-24um.fits. It should look like this: Once you have opened an image you can change the display in two forms to get a better look at the data. This is called changing the “stretch” of the image. First you can press the left mouse button and hold it down and move the mouse. This will change the relative brightness on the screen. If you only have one mouse button, which is typical on Apple computers, don't worry! You can jump straight to the second way of stretching the image. You also could try pressing either the "option" key, or the down- arrow key (if you have one) at the same time as pressing your mouse button. Second you can apply a mathematical function to the image. This is the most useful method since often the main problem is that there are very bright and very faint things in an image so trying to display both simultaneously is difficult. But if you apply a logarithm function to the images where each pixel value is replaced by the log of that value then it becomes easier to see bright things next to faint things. For example if one pixel has a value of 10 and the pixel next to it is 10 times brighter and has a value of 100, it is difficult to analyze. But if you took the log of both pixel values then their pixel values change from 10 and 100 to 1 and 2 (log(10)=1, log(100)=2) so it become easier to see the brighter value next to the fainter one. Go to the “Scaling” menu and select “log” for the image you have loaded. You can still use the left mouse button to change the relative brightness on the screen. A final way to change the display is to change the minimum (Min) and maximum (Max) values displayed. If the image has a value higher than the maximum you specify, all pixels higher than that maximum value are displayed as if they had that maximum value. Similarly, if you specify a minimum value to plot, image values lower than that are treated as if they have the minimum value. You specify the minimum and maximum values in the upper middle of the ATV window, just to the left of the two small images. Change those numbers to see how the image changes. Now you are ready to do photometry. 3. Determining the Light From the AGN Photometry is the measurement of the brightness of an object. The brightness that is recorded on an electronic detector (or any kind of detector) is a combination of the brightness of the source plus the brightness of the background that the source is on. In the case of the center of the galaxy above, a great deal of the "background" is in fact from the surrounding host galaxy. But what we are interested in is only the light from the center and not from the rest of the galaxy. To account for this, we will determine how much light is coming from where the center of the AGN is, and then compare it to how much light is coming from near the center of the AGN. We assume that the "background" near the AGN is the same as the background right on the AGN, so by subtracting the two, we are left with only the brightness of the center of the AGN. To start the photometry process, place the cursor on the center of the galaxy (or in general on whatever you want to do photometry on) and press the “P” key. Notice that on the upper right of ATV, there is a window that magnifies the region your cursor is on, or you can simply zoom in using the “ZoomIn” function just above the image. Once you press “P,” then a new window opens with a magnified region around where your cursor was with 3 circles drawn around your photometry target. The green circle is around the target whose light you want to measure and it is called your “photometry aperture.” The blue and purple circles define a ring in which the sky measurement will be made which will give the average background value per pixel that will be subtracted from each pixel within the aperture value. Then after all the pixels within the photometry aperture have this average per pixel sky value subtracted from them, they are totaled up and are displayed on the right as “Object Counts: 53770.5” The next step revolves around the radius of the photometry aperture. How do you know if it is big enough or maybe if it is too big? To see if you have included the light mainly from the center and not mostly from the background, press the “Show Radial Profile” key: This is a one dimensional representation of the image. The brightest part of the image is at zero radius on the x-axis (the numbers are partially hidden at the bottom of the screen) and has the most counts (2300 counts on the y-axis). But as you go away from the center of the image and to the right on the plot you see that the counts come down and then they are almost flat but they don’t actually reach zero counts. This is because there is background or sky contribution which in this case comes from the rest of the host galaxy and is noted in red as “sky level.” The sky level is measured within a ring between the inner sky measurement radius (insky) and the outer sky measurment radius (outsky).
Load more

Recommended publications
  • Guide for the Use of the International System of Units (SI)
    Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S.
    [Show full text]
  • The Equation of Radiative Transfer How Does the Intensity of Radiation Change in the Presence of Emission and / Or Absorption?
    The equation of radiative transfer How does the intensity of radiation change in the presence of emission and / or absorption? Definition of solid angle and steradian Sphere radius r - area of a patch dS on the surface is: dS = rdq ¥ rsinqdf ≡ r2dW q dS dW is the solid angle subtended by the area dS at the center of the † sphere. Unit of solid angle is the steradian. 4p steradians cover whole sphere. ASTR 3730: Fall 2003 Definition of the specific intensity Construct an area dA normal to a light ray, and consider all the rays that pass through dA whose directions lie within a small solid angle dW. Solid angle dW dA The amount of energy passing through dA and into dW in time dt in frequency range dn is: dE = In dAdtdndW Specific intensity of the radiation. † ASTR 3730: Fall 2003 Compare with definition of the flux: specific intensity is very similar except it depends upon direction and frequency as well as location. Units of specific intensity are: erg s-1 cm-2 Hz-1 steradian-1 Same as Fn Another, more intuitive name for the specific intensity is brightness. ASTR 3730: Fall 2003 Simple relation between the flux and the specific intensity: Consider a small area dA, with light rays passing through it at all angles to the normal to the surface n: n o In If q = 90 , then light rays in that direction contribute zero net flux through area dA. q For rays at angle q, foreshortening reduces the effective area by a factor of cos(q).
    [Show full text]
  • Relationships of the SI Derived Units with Special Names and Symbols and the SI Base Units
    Relationships of the SI derived units with special names and symbols and the SI base units Derived units SI BASE UNITS without special SI DERIVED UNITS WITH SPECIAL NAMES AND SYMBOLS names Solid lines indicate multiplication, broken lines indicate division kilogram kg newton (kg·m/s2) pascal (N/m2) gray (J/kg) sievert (J/kg) 3 N Pa Gy Sv MASS m FORCE PRESSURE, ABSORBED DOSE VOLUME STRESS DOSE EQUIVALENT meter m 2 m joule (N·m) watt (J/s) becquerel (1/s) hertz (1/s) LENGTH J W Bq Hz AREA ENERGY, WORK, POWER, ACTIVITY FREQUENCY second QUANTITY OF HEAT HEAT FLOW RATE (OF A RADIONUCLIDE) s m/s TIME VELOCITY katal (mol/s) weber (V·s) henry (Wb/A) tesla (Wb/m2) kat Wb H T 2 mole m/s CATALYTIC MAGNETIC INDUCTANCE MAGNETIC mol ACTIVITY FLUX FLUX DENSITY ACCELERATION AMOUNT OF SUBSTANCE coulomb (A·s) volt (W/A) C V ampere A ELECTRIC POTENTIAL, CHARGE ELECTROMOTIVE ELECTRIC CURRENT FORCE degree (K) farad (C/V) ohm (V/A) siemens (1/W) kelvin Celsius °C F W S K CELSIUS CAPACITANCE RESISTANCE CONDUCTANCE THERMODYNAMIC TEMPERATURE TEMPERATURE t/°C = T /K – 273.15 candela 2 steradian radian cd lux (lm/m ) lumen (cd·sr) 2 2 (m/m = 1) lx lm sr (m /m = 1) rad LUMINOUS INTENSITY ILLUMINANCE LUMINOUS SOLID ANGLE PLANE ANGLE FLUX The diagram above shows graphically how the 22 SI derived units with special names and symbols are related to the seven SI base units. In the first column, the symbols of the SI base units are shown in rectangles, with the name of the unit shown toward the upper left of the rectangle and the name of the associated base quantity shown in italic type below the rectangle.
    [Show full text]
  • CHAPTER 2: Radiometric Measurements Principles REFERENCE: Remote Sensing of the Environment John R
    CHAPTER 2: Radiometric Measurements Principles REFERENCE: Remote Sensing of the Environment John R. Jensen (2007) Second Edition Pearson Prentice Hall Energy-matter interactions in the atmosphere at the study area and at the remote sensor detector RADIANT ENERGY (Q): is the energy carried by a photon. Unit: Joules (J) RADIANT FLUX (Φ): is the time rate of flow of radiant energy. Unit: watts (W = J s-1) Φ = dQ = Joules = Watts dt seconds A derivative is the instantaneous rate of change of a function. RADIANT INTENSITY (I): Is a measure of the radiant flux proceeding from the source per unit solid angle in a specified direction. Unit: watts steradian-1 I = dΦ = watts dω steradian Solid Angle (ω ó Ω): Is equal to the spherical surface area (A) divided by the square of the radius (r). Unit: steradian Ω = A/r2 Radiance (L) Radiance in certain wavelengths (L)is: -the radiant flux (Φ) -per unit solid angle () -leaving an extended source area L in a given direction () Acos -per unit projected source area (A) Units: watts per meter squared per steradian (W m-2 sr -1 ) L is a function of direction, therefore the zenith and azimuth angles must be considered. The concept of radiance leaving a specific projected source area on the ground, in a specific direction, and within a specific solid angle. FIELD RADIOMETRY Lλ Radiance (L) REFLECTANCE Sample Radiation () R() = __________________ Reference Radiation () x100 = Reflectance Percent REFLECTANCE RADIANCE FLUX DENSITY Irradiance is a measure of the amount of radiant flux incident upon a surface per unit area of the surface measured in watts m-2.
    [Show full text]
  • Radiometry and Photometry
    Radiometry and Photometry Wei-Chih Wang Department of Power Mechanical Engineering National TsingHua University W. Wang Materials Covered • Radiometry - Radiant Flux - Radiant Intensity - Irradiance - Radiance • Photometry - luminous Flux - luminous Intensity - Illuminance - luminance Conversion from radiometric and photometric W. Wang Radiometry Radiometry is the detection and measurement of light waves in the optical portion of the electromagnetic spectrum which is further divided into ultraviolet, visible, and infrared light. Example of a typical radiometer 3 W. Wang Photometry All light measurement is considered radiometry with photometry being a special subset of radiometry weighted for a typical human eye response. Example of a typical photometer 4 W. Wang Human Eyes Figure shows a schematic illustration of the human eye (Encyclopedia Britannica, 1994). The inside of the eyeball is clad by the retina, which is the light-sensitive part of the eye. The illustration also shows the fovea, a cone-rich central region of the retina which affords the high acuteness of central vision. Figure also shows the cell structure of the retina including the light-sensitive rod cells and cone cells. Also shown are the ganglion cells and nerve fibers that transmit the visual information to the brain. Rod cells are more abundant and more light sensitive than cone cells. Rods are 5 sensitive over the entire visible spectrum. W. Wang There are three types of cone cells, namely cone cells sensitive in the red, green, and blue spectral range. The approximate spectral sensitivity functions of the rods and three types or cones are shown in the figure above 6 W. Wang Eye sensitivity function The conversion between radiometric and photometric units is provided by the luminous efficiency function or eye sensitivity function, V(λ).
    [Show full text]
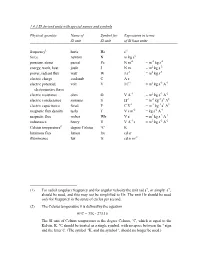
  • 1.4.3 SI Derived Units with Special Names and Symbols
    1.4.3 SI derived units with special names and symbols Physical quantity Name of Symbol for Expression in terms SI unit SI unit of SI base units frequency1 hertz Hz s-1 force newton N m kg s-2 pressure, stress pascal Pa N m-2 = m-1 kg s-2 energy, work, heat joule J N m = m2 kg s-2 power, radiant flux watt W J s-1 = m2 kg s-3 electric charge coulomb C A s electric potential, volt V J C-1 = m2 kg s-3 A-1 electromotive force electric resistance ohm Ω V A-1 = m2 kg s-3 A-2 electric conductance siemens S Ω-1 = m-2 kg-1 s3 A2 electric capacitance farad F C V-1 = m-2 kg-1 s4 A2 magnetic flux density tesla T V s m-2 = kg s-2 A-1 magnetic flux weber Wb V s = m2 kg s-2 A-1 inductance henry H V A-1 s = m2 kg s-2 A-2 Celsius temperature2 degree Celsius °C K luminous flux lumen lm cd sr illuminance lux lx cd sr m-2 (1) For radial (angular) frequency and for angular velocity the unit rad s-1, or simply s-1, should be used, and this may not be simplified to Hz. The unit Hz should be used only for frequency in the sense of cycles per second. (2) The Celsius temperature θ is defined by the equation θ/°C = T/K - 273.15 The SI unit of Celsius temperature is the degree Celsius, °C, which is equal to the Kelvin, K.
    [Show full text]
  • International System of Units （Si）
    ［TECHNICAL DATA］ INTERNATIONAL SYSTEM OF UNITS（ SI） Excerpts from JIS Z 8203（ 1985） 1. The International System of Units（ SI） and its usage 1－3. Integer exponents of SI units 1－1. Scope of application This standard specifies the International System of Units（ SI） and how to use units under the SI system, as well as （1） Prefixes The multiples, prefix names, and prefix symbols that compose the integer exponents of 10 for SI units are shown in Table 4. the units which are or may be used in conjunction with SI system units. Table 4. Prefixes 1 2. Terms and definitions The terminology used in this standard and the definitions thereof are as follows. － Multiple of Prefix Multiple of Prefix Multiple of Prefix （1） International System of Units（ SI） A consistent system of units adopted and recommended by the International Committee on Weights and Measures. It contains base units and supplementary units, units unit Name Symbol unit Name Symbol unit Name Symbol derived from them, and their integer exponents to the 10th power. SI is the abbreviation of System International d'Unites（ International System of Units）. 1018 Exa E 102 Hecto h 10−9 Nano n （2） SI units A general term used to describe base units, supplementary units, and derived units under the International System of Units（ SI）. 1015 Peta P 10 Deca da 10−12 Pico p （3） Base units The units shown in Table 1 are considered the base units. 1012 Tera T 10−1 Deci d 10−15 Femto f （4） Supplementary units The units shown in Table 2 below are considered the supplementary units.
    [Show full text]
  • The International System of Units (SI) - Conversion Factors For
    NIST Special Publication 1038 The International System of Units (SI) – Conversion Factors for General Use Kenneth Butcher Linda Crown Elizabeth J. Gentry Weights and Measures Division Technology Services NIST Special Publication 1038 The International System of Units (SI) - Conversion Factors for General Use Editors: Kenneth S. Butcher Linda D. Crown Elizabeth J. Gentry Weights and Measures Division Carol Hockert, Chief Weights and Measures Division Technology Services National Institute of Standards and Technology May 2006 U.S. Department of Commerce Carlo M. Gutierrez, Secretary Technology Administration Robert Cresanti, Under Secretary of Commerce for Technology National Institute of Standards and Technology William Jeffrey, Director Certain commercial entities, equipment, or materials may be identified in this document in order to describe an experimental procedure or concept adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the entities, materials, or equipment are necessarily the best available for the purpose. National Institute of Standards and Technology Special Publications 1038 Natl. Inst. Stand. Technol. Spec. Pub. 1038, 24 pages (May 2006) Available through NIST Weights and Measures Division STOP 2600 Gaithersburg, MD 20899-2600 Phone: (301) 975-4004 — Fax: (301) 926-0647 Internet: www.nist.gov/owm or www.nist.gov/metric TABLE OF CONTENTS FOREWORD.................................................................................................................................................................v
    [Show full text]
  • SI QUICK REFERENCE GUIDE: International System of Units (SI) the Modernized Metric System*
    SI QUICK REFERENCE GUIDE: International System of Units (SI) The Modernized Metric System* UNITS The International System of Units (SI) is based on seven fundamental (base) units: Base Units Quantity Name Symbol length metre m mass kilogram kg time second s electric current ampere A thermodynamic temperature kelvin K amount of substance mole mol luminous intensity candela cd and a number of derived units which are combinations of base units and which may have special names and symbols: Examples of Derived Units Quantity Expression Name Symbol acceleration angular rad/s2 linear m/s2 angle plane dimensionless radian rad solid dimensionless steradian sr area m2 Celsius temperature K degree Celsius °C density heat flux W/ m2 mass kg/m3 current A/m2 energy, enthalpy work, heat N • m joule J specific J/ kg entropy heat capacity J/ K specific J/ (kg•K) flow, mass kg/s flow, volume m3/s force kg • m/s2 newton N frequency periodic 1/s hertz Hz rotating rev/s inductance Wb/A henry H magnetic flux V • s weber Wb mass flow kg/s moment of a force N • m potential,electric W/A volt V power, radiant flux J/s watt W pressure, stress N/m2 pascal Pa resistance, electric V/A ohm Ω thermal conductivity W/(m • K) velocity angular rad/s linear m/s viscosity dynamic (absolute)(µ)Pa• s kinematic (ν)m2/s volume m3 volume, specific m3/kg *For complete information see IEEE/ASTM SI-10. SI QUICK REFERENCE GUIDE SYMBOLS Symbol Name Quantity Formula A ampere electric current base unit Bq becquerel activity (of a radio nuclide) 1/s C coulomb electric charge A • s °C
    [Show full text]
  • Radiometry and Photometry
    Radiometry and Photometry Wei-Chih Wang Department of Power Mechanical Engineering National TsingHua University Week 15 • Course Website: http://courses.washington.edu/me557/optics • Reading Materials: - Week 15 reading materials are from: http://courses.washington.edu/me557/readings/ • HW #2 due Week 16 • Set up a schedule to do Lab 2 (those who havne’t done the lab, you can do some designs projects relating to LED and detectors and send them to me before 6/25) • Prism Design Project memo and presentation due next two weeks (here are things you need to send me, video of your oral presentation with demo, PPTs, memos) • Final Project proposal: Due Today (please follow the instruction on what you need to include in your proposal) • Final Project Presentation on 6/7 (We will not do the final presentation on 6/7, but instead you will send me the videos of your oral presentations and demos along with your PPTs on 6/8) • Final project report and all the missing HW’s must be turned in by 6/19 5PM • Please send all these appropriate assignment and project materials to [email protected] according to the due dates. Again, I need videos of your oral presentations and demos besides your PPTs and reports or memos. w.wang 2 Last Week • Photodetectors - Photoemmissive Cells - Semiconductor Photoelectric Transducer (diode equation, energy gap equation, reviser bias voltage, quantum efficiency, responsivity, junction capacitance, detector angular response, temperature effect, different detector operating mode, noises in detectors, photoconductive, photovoltaic,
    [Show full text]
  • 1. 2 Photometric Units
    4 CHAPTERl INTRODUCTION 1. 2 Photometric units Before starting to describe photomultiplier tubes and their characteristics,this section briefly discusses photometric units commonly used to measurethe quantity of light. This section also explains the wavelength regions of light (spectralrange) and the units to denotethem, as well as the unit systemsused to expresslight intensity. Since information included here is just an overview of major photometric units, please refer to specialty books for more details. 1. 2. 1 Spectral regions and units Electromagneticwaves cover a very wide rangefrom gammarays up to millimeter waves.So-called "light" is a very narrow range of theseelectromagnetic waves. Table 1-1 showsdesignated spectral regions when light is classified by wavelength,along with the conver- sion diagram for light units. In general, what we usually refer to as light covers a range from 102to 106 nanometers(nm) in wavelength. The spectral region between 350 and 70Onmshown in the table is usually known as the visible region. The region with wavelengthsshorter than the visible region is divided into near UV (shorter than 35Onrn),vacuum UV (shorter than 200nm) where air is absorbed,and extremeUV (shorter than 100nm). Even shorter wavelengthsspan into the region called soft X-rays (shorter than IOnrn) and X- rays. In contrast, longer wavelengths beyond the visible region extend from near IR (750nm or up) to the infrared (severalmicrometers or up) and far IR (severaltens of micrometers) regions. Wavelength Spectral Range Frequency Energy nm (Hz) (eV) X-ray Soft X-ray 10 102 1016 ExtremeUV region 102 10 Vacuum UV region 200 Ultravioletregion 10'5 350 Visible region 750 103 Near infraredregion 1 1014 104 Infrared region 10-1 1013 105 10-2 Far infrared region 1012 106 10-3 .
    [Show full text]
  • Light and Motion
    Light and Motion Erik G. Learned-Miller Department of Computer Science University of Massachusetts, Amherst Amherst, MA 01003 December 10, 2009 Abstract 1 1 Analyzing the movement of light The goal of this section is to make sure that you understand some basic ideas about the emission of light, its interaction with surfaces, and its propagation through lenses. Some ideas, like the “inverse square” law, should be easy to remember once you un- derstand the intuition behind them. 1.1 Point sources of light We start with a discussion of point light sources. This is a simplified model of any small or distant light source, such as a distant light bulb, a star, or perhaps the sun, in which we treat it as though it were an infinitesimal point. Of course, we know that no light source is infinitely small, but assuming that it is a point can make certain analyses simpler. Any light source has associated with it a power output, which is the amount of energy consumed per unit of time (for example, joules per second). A common unit of power associated with light sources is the watt. For example, most of us are familiar with using 60-watt or 100-watt light bulbs. While this power rating refers to the amount of power consumed by the bulb, rather than the amount of power produced as light, for this discussion, we will assume that the power consumed and the power output as light are the same. As another example, the wattage of the sun is about 3.846 × 1026 watts.
    [Show full text]