Manuscript Final for HUSCAP.Pdf
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

2015 49Th Congress, Sapporo, Hokkaido, Japan
Applied ethology 2015: Ethology for sustainable society ISAE2015 Proceedings of the 49th Congress of the International Society for Applied Ethology 14-17 September 2015, Sapporo Hokkaido, Japan Ethology for sustainable society edited by: Takeshi Yasue Shuichi Ito Shigeru Ninomiya Katsuji Uetake Shigeru Morita Wageningen Academic Publishers Buy a print copy of this book at: www.WageningenAcademic.com/ISAE2015 This work is subject to copyright. All rights are reserved, whether the whole or part of the material is concerned. Nothing from this publication may be translated, reproduced, stored in a computerised system or published in any form or in any manner, including electronic, mechanical, reprographic or photographic, without prior written permission from the publisher: Wageningen Academic Publishers P.O. Box 220 EAN: 9789086862719 6700 AE Wageningen e-EAN: 9789086868179 The Netherlands ISBN: 978-90-8686-271-9 www.WageningenAcademic.com e-ISBN: 978-90-8686-817-9 [email protected] DOI: 10.3920/978-90-8686-817-9 The individual contributions in this publication and any liabilities arising from them remain First published, 2015 the responsibility of the authors. The publisher is not responsible for possible © Wageningen Academic Publishers damages, which could be a result of content The Netherlands, 2015 derived from this publication. ‘Sustainability for animals, human life and the Earth’ On behalf of the Organizing Committee of the 49th Congress of ISAE 2015, I would like to say fully welcome for all of you attendances to come to this Congress at Hokkaido, Japan! Now a day, our animals, that is, domestic, laboratory, zoo, companion, pest and captive animals or managed wild animals, and our life are facing to lots of problems. -

RADIOACTIVITY SURVEY DATA in Japan
RADIOACTIV SURVEY D」A ln Al)ri11963,in compli seLforthbytheJapanAtomi the Division oE Radioactiv Institute ofRadiologicalSci( 1.Collect,rCCOrd and on radiation from Natiorl 2.Analyze theinform之】 3.Establish a radiatior exchange center. As a p;lrt Of thc asく thc Nationwidc R;ldioactiv Were aSSClnbled an〔1coll叩il Prcscntl)1ans are toissuet On a quarterly basis. For furtherinformatioI POrtedin thisissue,rCadcr5 COntributorsindicatedin th RadioactivitySurveyDa inJapan Number 4 AⅦguSt1964 Comtents Page MeteorogictlData I)ieta Strontium-90and Cesium-137in Rain andDry Strontium-90and Cesiu] Fallout(Jbpan AnalyticalChemistry (肋如彿αZ血βま宜紬fβ Rβgβαγ¢九九β招%fβ)………………….1 ぶ¢宜β%¢ββ)‥.‥‥‥. (九pα≠A≠α‡〃抽αZ( GeograpbicalData ∫九βf宜紬fβ)‥.‥.‥‥ Strontium-90and Cesium-137in Soil Strontium-90and Cesiul (抽出0耽α£∫朋f宜f≠fβげ月αd宜0~og宜¢α乙 (九pα彿A≠α如£¢αい ぶβ£β≠¢ββ)‥.‥‥‥‥.‥‥‥‥‥.‥‥‥ J九β£宜紬fβ)‥‥‥‥‥ (九pα彿A≠α‡〃士官¢αZC九β刑由fγyRβg紺γ¢九 (乃αγαg宜Pγ小β£≠γβ 力ほ抽加ゎ)…………………………‥ 7 Strontium-90and Cesiu] Water Data (九pαれA%α如ま¢αヱ・ Strontium-90and Cesium-137in City Water ∫れβf宜ねfβ)‥‥.‥‥. (抽出0≠α~∫≠βま宜ねまβq′Rαd宜0わgieα£ Strontium-90andCesiuI ぶ¢宜β竹βββ).‥‥‥‥‥‥.‥‥‥‥‥.‥.‥ (tねpα雅Aれα如宜eα‡・ (九pα≠A≠αZyfま¢α乙C九β例言8fγyRβββαγC九 ∫那f宜f髄fβ).‥‥‥‥. ● MeteorologlCalData Strontium-90and Cesium-137in Rain and Dry Fallout (九pα彿A≠α如宜¢α‡C九β例言β£γ財月βββαγC九∫れβ£加古β) SinceMay1963,theJapanAnalyticalChemistry StrOntium and cesium c王 ResearchInstitute,On COmmission bytheScience COlumn fi11ed with sodil] andTechnologyAgency,hasmeasuredstrontium-90 resin(Dowex 50W-Ⅹ8, and cesium-137 contentin monthly deposits at COlumn was sent totheJ VariouslocationsthroughoutJapan.Samplingand ResearchInstitute for m. for Pre-treatment concentration have been carried used wasillustratedin Outby24prefecturalpublic healthlaboratories. this publication. The tray recommended by the Science and After a fraction conl TechnologyAgencyhasacollectionareaof5,000cm2, and cesium-137was elut( to andis exposed rain and dust throughout the ChemicalanalysIS WaS Ca二 depth month・The of waterin the trayiskept recommendedbytheScien to atlOmm preventdust from beingblown away. -

A Synopsis of the Parasites from Cyprinid Fishes of the Genus Tribolodon in Japan (1908-2013)
生物圏科学 Biosphere Sci. 52:87-115 (2013) A synopsis of the parasites from cyprinid fishes of the genus Tribolodon in Japan (1908-2013) Kazuya Nagasawa and Hirotaka Katahira Graduate School of Biosphere Science, Hiroshima University Published by The Graduate School of Biosphere Science Hiroshima University Higashi-Hiroshima 739-8528, Japan December 2013 生物圏科学 Biosphere Sci. 52:87-115 (2013) REVIEW A synopsis of the parasites from cyprinid fishes of the genus Tribolodon in Japan (1908-2013) Kazuya Nagasawa1)* and Hirotaka Katahira1,2) 1) Graduate School of Biosphere Science, Hiroshima University, 1-4-4 Kagamiyama, Higashi-Hiroshima, Hiroshima 739-8528, Japan 2) Present address: Graduate School of Environmental Science, Hokkaido University, N10 W5, Sapporo, Hokkaido 060-0810, Japan Abstract Four species of the cyprinid genus Tribolodon occur in Japan: big-scaled redfin T. hakonensis, Sakhalin redfin T. sachalinensis, Pacific redfin T. brandtii, and long-jawed redfin T. nakamuraii. Of these species, T. hakonensis is widely distributed in Japan and is important in commercial and recreational fisheries. Two species, T. hakonensis and T. brandtii, exhibit anadromy. In this paper, information on the protistan and metazoan parasites of the four species of Tribolodon in Japan is compiled based on the literature published for 106 years between 1908 and 2013, and the parasites, including 44 named species and those not identified to species level, are listed by higher taxon as follows: Ciliophora (2 named species), Myxozoa (1), Trematoda (18), Monogenea (0), Cestoda (3), Nematoda (9), Acanthocephala (2), Hirudinida (1), Mollusca (1), Branchiura (0), Copepoda (6 ), and Isopoda (1). For each taxon of parasite, the following information is given: its currently recognized scientific name, previous identification used for the parasite occurring in or on Tribolodon spp.; habitat (freshwater, brackish, or marine); site(s) of infection within or on the host; known geographical distribution in Japan; and the published source of each locality record. -

R98.23.01. Hokkaido Rev 1
HOKKAIDO, JAPAN, Mw 6.7 EARTHQUAKE OF SEPTEMBER 6, 2018 LIFELINE PERFORMANCE By JOHN M EIDINGER and ALEX K TANG The Council of Lifeline Earthquake Engineering TCLEE No. 4 G&E Report R98.23.01 Revision 1, March 18 2019 Hokkaido Mw 6.7 Earthquake of Sept 6 2018 R98.23.01 Rev. 1. March 18 2019 TAble of Contents TABLE OF CONTENTS ............................................................................................................................... I ABSTRACT .................................................................................................................................................... 1 PREFACE ...................................................................................................................................................... 3 AUTHORS’ AFFILIATIONS ...................................................................................................................... 4 ACKNOWLEDGEMENTS .......................................................................................................................... 6 REPORT COVER PHOTOS ...................................................................................................................... 13 ENDORSEMENTS ...................................................................................................................................... 13 1.0 INTRODUCTION ................................................................................................................................. 14 1.1 LIMITATIONS ....................................................................................................................................... -

Survey of PWRI 2012
Joint Research and Partnership with Other Organizations Joint Research We conduct joint research with research organizations such as private corporations and universities to promote more efficient and effective research and development. Joint research includes an external research organization participating in PWRI-proposed research topics, i.e. “PWRI proposed project”, and projects conducted in response to a proposal from an external organization, i.e. “private proposed project”. During the 3rd period of our medium-term goals, we are scheduled to conduct approximately 100 joint projects annually in an effort to create high-quality research results. Joint Research Project System Diagram PWRI proposed joint research project Private proposed joint research project Present Setting Proposing a research topic a research area technology Joint research project Private Joint research project Private PWRI sector, etc. PWRI sector, etc. Joint research project for which PWRI presents a research Joint research project for which PWRI sets a research area, receives proposals through public posting and designates topic, and publicly seeks or designates a partner a private, etc. partner who proposes unique and innovative technology Effects of efficiency-focused joint research system Discover technical seeds possessed by private sector Use part of intellectual property possessed by private sector Creation of high-quality research results Dissemination/Promotion of research results Alliance with other organizations PWRI makes Agreements for Civil Engineering Technology Alliance/Cooperation with local governments, universities and other research institutions, and strives to create better and more ample research results for the purpose of contributing to the efficient development of high-quality infrastructure under a comprehensive civil engineering technology alliance and in mutual cooperation. -

5. Revival of Salmon Resources and Restoration of a Traditional Ritual Of
5 Revival of Salmon Resources and Restoration of a Traditional Ritual of the Ainu, the Indigenous People of Japan Yōsuke Kosaka How Ainu people have traditionally regarded salmon Among the Ainu gods’ tales compiled and translated into Japanese by the young Ainu woman, Yukie Chiri, two stories out of 13 were on the theme of salmon. Yukie died at the age of 19 in 1922; however, her work has been well-known in Japan through her beautiful poetic translations, such as the following: ‘Silver droplets falling, falling all around, golden droplets falling, falling all around’ (Chiri 1978: 11). One of the tales about salmon begins with a scene in which, ‘A vicious man changed a clear stream into poisonous water by setting up walnut tree trunks in the river’ (Chiri 1978: 135). As a result, the salmon could not come back to the headwaters. Having discovered such a malicious act, a son of Okikirmuy, a personal god of the Ainu, fights against the spiteful man and finally defeats him in order to recover the clean water and salmon. This tale, I think, reminds us how important it is to protect the river environment for the salmon. 69 INDIGENOUS EFFLORESCENCE The Ainu people regarded famine as being caused by the misconduct of humans. An Ainu oral tradition tells of the God Who Controls Hunting Lands being informed that a human village was suffering from famine. When the god inquired the reason from another god whose spirit possesses the salmon, and from yet another god whose spirit possesses the deer, the God of Salmon answered that humans had forgotten to use a particular wooden stick when killing the salmon, which allows their souls to return to the gods’ world. -

Iha Applications
IHA APPLICATIONS This database is a summary of many of the applications of the Indicators of Hydrologic Alteration (IHA) software. Entries are listed according to author, with the name of the body/s of water highlighted in bold type. Individual users of IHA submitted some of the entries, and those persons have authorized themselves as contacts to obtain addition information. Other information was culled from public documents, published reports, journal articles and business correspondence. The reasons for IHA usage fall into four categories: 1. Hydrologic Research: Use of the IHA software in assessing changes in hydrologic conditions (e.g. river flows, lake levels) over time, including changes caused by water management activities (dams, diversions, ground water pumping), climate shifts, changes in land use, etc. 2. Ecological Research: Use of the IHA software in assessing connections between hydrologic conditions (or changes in these conditions) and ecological responses, including studies of the influence of specific hydrologic conditions on species, plant community types, or ecological processes such as sediment transport, and salinity distributions. 3. Environmental Flow Recommendations: Use of the IHA software to develop recommendations for environmental flow protection (also commonly referred to as instream flows or ecosystem flows). Papers in this category may include application of the "Range of Variability Approach" (RVA) component of the IHA software. 4. Other: All other uses of the IHA software that do not fit into the above categories. IHA DATABASE Alber, M. & Flory, J. 2002. The Effects of Changing Freshwater Inflow to Estuaries: A Georgia Perspective. Georgia Coastal Research Council. 3 The intrusion of saltwater in the upper Florida aquifier is of increasing concern due to population growth and the increase in water demands. -

Calendar of Events July 2015 Notes: 1
Calendar of Events July 2015 Notes: 1. Published by Tourist Information Center of Japan National Tourism Organization and all rights reserved. Reproduction in whole or in part without written permission is prohibited. ©2015 Japan National Tourism Organization 2. Dates, times and functions are subject to change without notice. Especially schedule of outdoor events and flower festival may change due to the weather. Be sure to check the latest information in advance. 3. The access shows only major route. Please refer to following URL for alternative transportation from the station where you want to start. http://www.hyperdia.com/en/ 4. Japanese words appearing in the column provide the name of the event, the place and access for you to point out to Japanese passerby when you need help. 5. Please refer to URL (basically in Japanese) for each event. If you have further questions, please call TIC, JNTO at following number. TIC, JNTO Tel : (03)-3201-3331 from overseas +81 3 3201 3331 七夕 TsuyuTanabata 梅雨 TsuyuTanabata, is the Star rainy Festival season is heldin early on Julysummer 7 in mostin Japan. parts It ofusually Japan starts or August 7 in some areas. Based on a Chinese folk legend in which two Glossary: around the beginning of June and ends in mid-July. Special Remarks: starts - Altair (Cowherd) and Vega (Weaver) - love each other but Horen Palanquin Hokkaido, the northern part of Japan, is least affected by Tsuyu. Dates and Times are shown as follows which is common in Japan. only allowed to cross the Milky Way to meet once a year on this day. -

Natural Disaster and Coastal Geomorphology Natural Disaster and Coastal Geomorphology Shigeko Haruyama • Toshihiko Sugai Editors
Shigeko Haruyama · Toshihiko Sugai Editors Natural Disaster and Coastal Geomorphology Natural Disaster and Coastal Geomorphology Shigeko Haruyama • Toshihiko Sugai Editors Natural Disaster and Coastal Geomorphology 123 Editors Shigeko Haruyama Toshihiko Sugai Mie University The University of Tokyo Tsu Tokyo Japan Japan ISBN 978-3-319-33812-5 ISBN 978-3-319-33814-9 (eBook) DOI 10.1007/978-3-319-33814-9 Library of Congress Control Number: 2016940115 © Springer International Publishing Switzerland 2016 This work is subject to copyright. All rights are reserved by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed. The use of general descriptive names, registered names, trademarks, service marks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use. The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the publisher nor the authors or the editors give a warranty, express or implied, with respect to the material contained herein or for any errors or omissions that may have been made. Printed on acid-free paper This Springer imprint is published by Springer Nature The registered company is Springer International Publishing AG Switzerland Preface Flooding, tsunami, and earthquake are important natural disaster issues for local people to understand the disaster process and to make evacuation method and reconstruction method in discussion in each local participant. -

July 2016 Calendar of Events
Calendar of Events July 2016 Notes: 1. Published by Tourist Information Center of Japan National Tourism Organization and all rights reserved. Reproduction in whole or in part without written permission is prohibited. ©2016 Japan National Tourism Organization 2. Dates, times and functions are subject to change without notice. Especially schedule of outdoor events and flower festival may change due to the weather. Be sure to check the latest information in advance. 3. The access shows only major route. Please refer to following URL for alternative transportation from the station where you want to start. http://www.hyperdia.com/en/ 4. Japanese words appearing in the column provide the name of the event, the place and access for you to point out to Japanese passerby when you need help. 5. Please refer to URL (basically in Japanese) for each event. If you have further questions, please call TIC, JNTO at following number. TIC, JNTO Tel : (03)-3201-3331 from overseas +81 3 3201 3331 Tanabata 七夕 Tanabata, Star Festival is held on July 7 in most parts of Japan or Glossary: August 7 in some areas. Based on a Chinese folk legend in which two Horen Palanquin Special Remarks: starts - Altair (Cowherd) and Vega (Weaver) - love each other but Kodomo-Kabuki Traditional play by boys Dates and Times are shown as follows which is common in Japan. only allowed to cross the Milky Way to meet once a year on this day. Matsuri Festival, Event Dates : M/D April 3 ⇒ 4/3 Wishes are written on long colored strips of paper and hung from a Mikoshi Portable shrine bamboo branch with other decorations. -

Computational Challenges in River Morphodynamics by Iric
Computational Challenges in River Morphodynamics by iRIC Yasuyuki Shimizu, Hokkaido University, Japan Yasuyuki Shimizu 清水 康行 Professor, Laboratory of Hydraulic and Research (Civil Engineering) Graduate School of Engineering Hokkaido University 北海道大学(札幌) Field of Interst: Water Related Disaster Prevention Research Hydraulic Engineering Water Resources Engineering Computational Fluid Dynamics, and Computational Models 2 Hokkaido Area: 83,000km2 SAPPORO Population: 5,700,000 Sapporo Population: 1,900,000 3 Where Hokkaido University is Main campus located in Sapporo, Hokkaido Hokkaido University Sapporo campus Another campus in Hakodate (Grad. School of Fisheries Sciences) Several off-campus facilities mostly in Hokkaido Established in 1876 11,000 Under Graduate Students 6,000 Graduate Students 2,000 Teaching Staff 1,800 Non-Teaching Staff 12 Faculties + 10 Institutes 5 6 7 K.Asahi, Y. Yoshida, H.Tsunematsu, Y. Shimizu and J. Nelson(2012), Development of the iRIC Software for River analysis 8 K.Asahi, Y. Yoshida, H.Tsunematsu, Y. Shimizu and J. Nelson(2012), Development of the iRIC Software for River analysis 9 K.Asahi, Y. Yoshida, H.Tsunematsu, Y. Shimizu and J. Nelson(2012), Development of the iRIC Software for River analysis 10 Typhoon passes between 1951 and 2018 of September 国立情報学研究所・デジタル台風サイトより12 August 2016 in Hokkaido Abashiri 網走 留萌Rumoi 旭川Asahi Kitami kawa 北見 Typhoon台風7号 #7 178/17th AUG上陸 Otaru小樽 札幌Sapporo 釧路 帯広Obihiro Kushiro Typhoon台風11号 #11 8/21th 上陸 室蘭Muroran 21 AUG Typhoon #10 Typhoon台風9 号#9 31th AUG台風10号 23th8/23AUG上陸 Hakodate函館 -
Research Findings and On-Site Case Studies
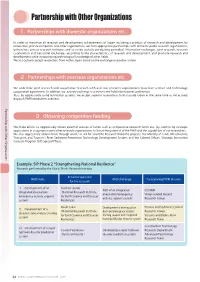
Partnership with Other Organizations 1. Partnerships with domestic organizations etc. In order to maximize all research and development achievements of Japan including a product of research and development by universities, private companies and other organizations, we form appropriate partnerships with domestic public research organizations, universities, private research institutes and so on by actively conducting periodical information exchanges, joint research, research cooperation and personnel exchanges according to the characteristics of research and development, and promote research and development while incorporating technological knowledge of other fields. We also actively accept researchers from within Japan based on the exchange researcher system. 2. Partnerships with overseas organizations etc. We undertake joint research and cooperative research with overseas research organizations based on science and technology cooperation agreements. In addition, we actively exchange researchers and hold international conferences. Also, by aggressively using fellowship systems, we accept superior researchers from outside Japan at the same time as we actively dispatch PWRI researchers overseas. Partnership with Other Organizations 3. Obtaining competitive funding We make efforts to aggressively obtain external sources of funds such as competitive research funds etc., by submitting strategic applications in cooperation with other research organizations, to boost the potential of the PWRI and the capabilities of our researchers. We also aggressively