DOCSLIB.ORG

Tripled Yield in Direct-Drive Laser Fusion Through Statistical Modelling V

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Tripled Yield in Direct-Drive Laser Fusion Through Statistical Modelling V ARTICLE https://doi.org/10.1038/s41586-019-0877-0 Tripled yield in direct-drive laser fusion through statistical modelling V. Gopalaswamy1,2*, R. Betti1,2,3, J. P. Knauer1, N. Luciani1,2,4, D. Patel1,2, K. M. Woo1,3, A. Bose1,5, I. V. Igumenshchev1, E. M. Campbell1, K. S. Anderson1, K. A. Bauer1, M. J. Bonino1, D. Cao1, A. R. Christopherson1,2, G. W. Collins1, T. J. B. Collins1, J. R. Davies1, J. A. Delettrez1, D. H. Edgell1, R. Epstein1, C. J. Forrest1, D. H. Froula1, V. Y. Glebov1, V. N. Goncharov1, D. R. Harding1, S. X. Hu1, D. W. Jacobs-Perkins1, R. T. Janezic1, J. H. Kelly1, O. M. Mannion1,3, A. Maximov1,2, F. J. Marshall1, D. T. Michel1, S. Miller1,2, S. F. B. Morse1, J. Palastro1, J. Peebles1, P. B. Radha1, S. P. Regan1, S. Sampat1, T. C. Sangster1, A. B. Sefkow1, W. Seka1, R. C. Shah1, W. T. Shmyada1, A. Shvydky1, C. Stoeckl1, A. A. Solodov1, W. Theobald1, J. D. Zuegel1, M. Gatu Johnson5, R. D. Petrasso5, C. K. Li5 & J. A. Frenje5 Focusing laser light onto a very small target can produce the conditions for laboratory-scale nuclear fusion of hydrogen isotopes. The lack of accurate predictive models, which are essential for the design of high-performance laser-fusion experiments, is a major obstacle to achieving thermonuclear ignition. Here we report a statistical approach that was used to design and quantitatively predict the results of implosions of solid deuterium–tritium targets carried out with the 30-kilojoule OMEGA laser system, leading to tripling of the fusion yield to its highest value so far for direct-drive laser fusion. When scaled to the laser energies of the National Ignition Facility (1.9 megajoules), these targets are predicted to produce a fusion energy output of about 500 kilojoules—several times larger than the fusion yields currently achieved at that facility. This approach could guide the exploration of the vast parameter space of thermonuclear ignition conditions and enhance our understanding of laser-fusion physics. Inertial confinement fusion (ICF)1–3 uses drivers such as lasers or where energy deposition by α particles is the dominant heating mech- pulsed power to implode a millimetre-size capsule made of a layer anism in the fusing plasma. Obtaining a burning plasma is considered of cryogenic deuterium (D) and tritium (T) enclosed within an abla- to be an important intermediate milestone on the path to ignition. tor shell composed of low-atomic-number material (typically a CH Recent publications provide detailed summaries of the indirect-17,18 polymer, high-density carbon or beryllium). The implosion produces and direct-drive19 efforts to achieve ignition, as well as an overview of copious amounts of DT fusion reactions, each producing a 14.1-MeV the current status of ICF13. neutron and a 3.5-MeV α particle. Laser ICF uses either direct illu- Historically, the design of ICF implosions has been primarily driven by mination of the capsule (direct drive)4 or indirect illumination of the one-dimensional (1D) and two-dimensional radiation–hydrodynamic capsule via X-rays produced by laser heating of a high-atomic-number (RH) codes20–24. Because of the substantial computational burden metal enclosure called a hohlraum (indirect drive)5. In direct-drive imposed by well resolved three-dimensional (3D) simulations, the laser fusion, laser light directly incident on the capsule surface at inten- use of 3D codes is mostly limited to post-shot simulations25,26. These sities of I ≈ 1015 W cm−2 drives mass ablation, which accelerates the simulations often include degradation sources (such as the ablator– shell inwards at velocities from 300 to 500 km s−1. As the shell con- fuel mix), engineering features (the stalk, fill tube or tent holding the verges, the central pressure increases and slows down the imploding capsule) and offsets from the target chamber centre to match experi- capsule. The central core reaches temperatures of several kiloelectron- mental observables post hoc, but cannot yet reliably predict the results volts, and the heat flux from the centre ablates fuel off the inner shell of a future experiment when changes to the target specifications and surface to form a low-density (30–100 g cm−3) central hot spot. This laser pulse shapes are made. At the Laboratory for Laser Energetics, the hot spot is confined by a nearly Fermi-degenerate6 (200–1,000 g cm−3) 1D RH code LILAC23 is used to design direct-drive implosions, with shell over a subnanosecond confinement time during which fusion experimentally benchmarked physics models for cross-beam energy reactions occur. If the areal density (ρR) of the compressed core is transfer27,28, thermal transport28,29 and first-principles models of the high enough, the α particles deposit their energy within the hot core, equation of state30. In part because of these improvements in com- driving a feedback process (known as alpha heating7–9) that amplifies puter modelling, experiments carried out with the OMEGA laser31 at the fusion reaction rates. Under the appropriate conditions of pres- energies of 26–28 kJ have demonstrated core compression that would sure, temperature and confinement time10–12, the alpha-heating process produce substantial fusion α-particle self-heating when scaled hydro- becomes intense enough to ‘ignite’ the central hot spot, resulting in dynamically to NIF energies (1.9 MJ)32,33 . Considerable performance a thermonuclear burn wave propagating radially through the entire improvements have also been achieved in indirect-drive ICF, with dense fuel, producing fusion energy yields many times greater than recent implosions of DT-layered targets producing over 50 kJ of fusion the driver energy input. Until now, demonstrating ignition via laser yield (about 2 × 1016 fusion reactions)14, greatly exceeding the energy fusion has been an elusive goal of the United States’ ICF Program13, input to the fusion fuel. although recent experiments14,15 using indirect drive at the National Despite the remarkable progress in modelling, it is still not possible to Ignition Facility (NIF)16 are approaching burning-plasma conditions7,8, predict a priori the results of an ICF experiment with enough accuracy 1Laboratory for Laser Energetics, University of Rochester, Rochester, NY, USA. 2Department of Mechanical Engineering, University of Rochester, Rochester, NY, USA. 3Department of Physics and Astronomy, University of Rochester, Rochester, NY, USA. 4Dipartimento di Energetica, Politecnico di Milano, Milan, Italy. 5Massachusetts Institute of Technology, Cambridge, MA, USA. *e-mail: [email protected] 31 JANUARY 2019 | VOL 565 | NATURE | 581 © 2019 Springer Nature Limited. All rights reserved. RESEARCH ARTICLE a Shot 80802 the DT ice34, or the ramp of the laser to full power, which is designed Ablator to adiabatically compress the shell. The late portion of the laser pulse 8.0 μm Ice 80802 can also be varied to prevent coasting of the shell or to launch a late 25 35 53 μm shock as in shock ignition . 20 The unexplored parameter space of the laser pulse shape and target specifications is vast, and today’s RH codes are not accurate enough to 15 Gas enable a high-confidence design of the optimum implosion that can 10 be applied at the existing ICF laser facilities. In addition, the param- 379 μm Power (TW) 5 eter space can be further extended if minor upgrades to the facility are included, such as changing the laser spot size on the target, the 0 target mount or the DT filling procedure19. It is not clear at this time 012 whether the lack of predictive capability in the RH codes is a result of Time (ns) inaccuracies in the physics models or of incomplete inputs provided b Shot 87266 to the codes or, as is most likely, both. It is clear, however, that the lack Ablator of predictive capability has hindered progress in improving the fusion yields in ICF. It is also clear that in this vast and unexplored parameter 7.4 μm 87266 Ice 25 space, there almost certainly exists a combination of target specifica- 42 μm tions, laser pulse shape and minor upgrades that leads to considerably 20 better performance than today’s implosions. 15 Here, we describe a new, statistically driven framework to aid in the Gas 10 traversal of this space, predict and design high-performance implo- Power (TW) sions and speed up the quest for thermonuclear ignition. The funda- 440 μm 5 mental principle behind this new framework is that even though the exp 0 RH codes are inaccurate, the experimental observables O are sim 012 expected to be correlated to the code output variables O because both the experiment and the code use the same input—that is, the laser Time (ns) pulse shape and the target geometry. Because the codes do not accurately reproduce the experimental results, the code–experiment expsim Fig. 1 | Target and laser pulse shape in the first phase of the relations are no longer one to one for each variable (Ojj≠ O ); Optimization Campaign. a, b, Shots 80802 (a) and 87266 (b) were the instead, a more global relation is theorized to exist, for which each first and last shot, respectively, of the first phase of the Optimization experimental observable is correlated to a combination of code output Campaign. The implosion design was guided by statistical methods and variables. led to the highest yield for direct-drive ICF. Design changes included To elucidate this approach, we use a set of parameters I1D to denote larger target radii, reductions of the DT ice thickness (reflected in the the initial conditions determining the 1D implosion dynamics (that is, changes to the gas, ice and ablator layer thicknesses shown on the left) and the laser pulse shape and target specifications) and S for the 3D non- substantial changes to the laser pulse shape.
Load more

Recommended publications
  • Progress Towards Polar-Drive Ignition for the NIF
    Home Search Collections Journals About Contact us My IOPscience Progress towards polar-drive ignition for the NIF This content has been downloaded from IOPscience. Please scroll down to see the full text. 2013 Nucl. Fusion 53 113021 (http://iopscience.iop.org/0029-5515/53/11/113021) View the table of contents for this issue, or go to the journal homepage for more Download details: IP Address: 198.125.179.18 This content was downloaded on 06/11/2013 at 22:08 Please note that terms and conditions apply. IOP PUBLISHING and INTERNATIONAL ATOMIC ENERGY AGENCY NUCLEAR FUSION Nucl. Fusion 53 (2013) 113021 (5pp) doi:10.1088/0029-5515/53/11/113021 Progress towards polar-drive ignition for the NIF R.L. McCrory1,a, R. Betti1,a, T.R. Boehly1, D.T. Casey2, T.J.B. Collins1, R.S. Craxton1, J.A. Delettrez1, D.H. Edgell1, R. Epstein1, J.A. Frenje2, D.H. Froula1, M. Gatu-Johnson2, V.Yu. Glebov1, V.N. Goncharov1, D.R. Harding1, M. Hohenberger1, S.X. Hu1, I.V. Igumenshchev1, T.J. Kessler1, J.P. Knauer1, C.K. Li2, J.A. Marozas1, F.J. Marshall1, P.W. McKenty1, D.D. Meyerhofer1,a, D.T. Michel1, J.F. Myatt1, P.M. Nilson1, S.J. Padalino3, R.D. Petrasso2, P.B. Radha1, S.P. Regan1, T.C. Sangster1, F.H. Seguin´ 2, W. Seka1, R.W. Short1, A. Shvydky1, S. Skupsky1, J.M. Soures1, C. Stoeckl1, W. Theobald1, B. Yaakobi1 and J.D. Zuegel1 1 Laboratory for Laser Energetics, University of Rochester, 250 East River Road, Rochester, NY 14623-1299, USA 2 Plasma Science Fusion Center, 173 Albany Street, Massachusetts Institute of Technology, Cambridge MA 02139, USA 3 Department of Physics, State University of New York at Geneseo, 1 College Circle, Geneseo NY 14454, USA E-mail: [email protected] Received 31 December 2012, accepted for publication 4 September 2013 Published 27 September 2013 Online at stacks.iop.org/NF/53/113021 Abstract The University of Rochester’s Laboratory for Laser Energetics (LLE) performs direct-drive inertial confinement fusion (ICF) research.
    [Show full text]
  • Fusion Ignition Via a Magnetically-Assisted Fast Ignition Approach
    Fusion ignition via a magnetically-assisted fast ignition approach W.-M. Wang1,3*, P. Gibbon2,4†, Z.-M. Sheng3,5,6‡, Y. T. Li1,3, and J. Zhang3,6 1Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, CAS, Beijing 100190, China 2Forschungszentrum Jülich GmbH, Institute for Advanced Simulation, Jülich Supercomputing Centre, D-52425 Jülich, Germany 3Collaborative Innovation Center of IFSA, Shanghai Jiao Tong University, Shanghai 200240, China 4Centre for Mathematical Plasma Astrophysics, Katholieke Universiteit Leuven, 3000 Leuven, Belgium 5SUPA, Department of Physics, University of Strathclyde, Glasgow G4 0NG, United Kingdom 6Key Laboratory for Laser Plasmas (MoE) and Department of Physics and Astronomy, Shanghai Jiao Tong University, Shanghai 200240, China * E-mail: [email protected] † E-mail: [email protected] ‡ E-mail: [email protected] 1 Significant progress has been made towards laser-driven fusion ignition via different schemes, including direct and indirect central ignition, fast ignition, shock ignition, and impact ignition schemes. However, to reach ignition conditions, there are still various technical and physical challenges to be solved for all these schemes. Here, our multi-dimensional integrated simulation shows that the fast-ignition conditions could be achieved when two 2.8 petawatt heating laser pulses counter-propagate along a 3.5 kilotesla external magnetic field. Within a period of 5 picoseconds, the laser pulses heat a nuclear fuel to reach the ignition conditions. Furthermore, we present the parameter windows of lasers and magnetic fields required for ignition for experimental test. To achieve controlled nuclear fusion energy, the central ignition concept of inertial confinement fusion (ICF) was proposed in 1970s [1-4].
    [Show full text]
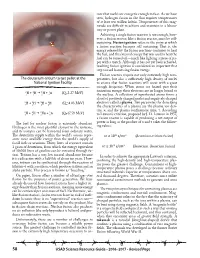
  • USAD Science Resource Guide • 2016–2017 • Revised Page The
    sure that nuclei are energetic enough to fuse. As we have seen, hydrogen fusion in the Sun requires temperatures of at least ten million kelvin. Temperatures of this mag- nitude are difficult to achieve and maintain in a labora- tory or power plant. Achieving a single fusion reaction is not enough, how- ever; a fusion reactor, like a fission reactor, must be self- sustaining. Fusion ignition refers to the point at which a fusion reaction becomes self-sustaining. That is, the energy released by the fusion reactions continues to heat the fuel, and the external energy that was used to heat the fuel can be turned off—much like lighting a piece of pa- per with a match. Although it has not yet been achieved, reaching fusion ignition is considered an important first step toward harnessing fusion energy. The deuterium-tritium target pellet at the Fusion reactors require not only extremely high tem- peratures, but also a sufficiently high density of nuclei National Ignition Facility. to ensure that fusion reactions will occur with a great enough frequency. When atoms are heated past their 2H + 2H 3H + 1n ionization energy, their electrons are no longer bound to 1 1 2 0 (Q=3.27 MeV) the nucleus. A collection of superheated atoms forms a cloud of positively charged nuclei and negatively charged 2H + 2 H 3 H + 1 H 1 1 1 1 (Q=4.03 MeV) electrons called a plasma. Two parameters for describing the characteristics of a plasma are the plasma ion den- τ 2H + 3H 4He + 1n sity, n, and the plasma confinement time, .
    [Show full text]
  • Road Map to Clean Energy Using Laser Beam Ignition of Boron-Hydrogen Fusion
    Laser and Particle Beams (2017), 35, 730–740. © Cambridge University Press, 2017 0263-0346/17 doi:10.1017/S0263034617000799 Road map to clean energy using laser beam ignition of boron-hydrogen fusion H. HORA,1 S. ELIEZER,2,4 G.J. KIRCHHOFF,3 N. NISSIM,2,5 J.X. WANG,6 P. LALOUSIS,7 Y.X. XU,6 8 4 9 9 G.H. MILEY, J.M. MARTINEZ-VAL, W. MCKENZIE, AND J. KIRCHHOFF 1Department of Theoretical Physics, University of New South Wales, Sydney 2052, Australia 2SOREQ Research Centre, Yavne, Israel 3UJG Management GmbH, 85586 Poing, Germany 4Polytechnique University, Madrid, Spain 5Department of Earth and Planetary Science, University of California, Berkeley, CA 94720, USA 6State Key Laboratory of Precision Spectroscopy, East China Normal University, Shanghai 200062, China 7Institute of Electronic Structure and Laser FORTH, Heraklion, Greece 8Department Nuclear, Plasma & Radiol. Engineering, University of Illinois, Urbana IL, USA 9HB11 Energy Pty. Ltd., Sydney, Australia (RECEIVED 26 September 2017; ACCEPTED 16 October 2017) Abstract With the aim to overcome the problems of climatic changes and rising ocean levels, one option is to produce large-scale sustainable energy by nuclear fusion of hydrogen and other very light nuclei similar to the energy source of the sun. Sixty years of worldwide research for the ignition of the heavy hydrogen isotopes deuterium (D) and tritium (T) have come close to a breakthrough for ignition. The problem with the DT fusion is that generated neutrons are producing radioactive waste. One exception as the ideal clean fusion process – without neutron production – is the fusion of hydrogen (H) with the boron isotope 11B11 (B11).
    [Show full text]
  • Late-Time Simulation of National Ignition Facility Hohlraums
    UCRL-JRNL-206693 Late-time simulation of National Ignition Facility Hohlraums D.C. Eder, O.S. Jones, M.M. Marinak, M.T. Tobin, B.J. MacGowan September 21, 2004 Nuclear Fusion 2004 Disclaimer This document was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor the University of California nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise, does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or the University of California. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or the University of California, and shall not be used for advertising or product endorsement purposes. Late-time simulation of National Ignition Facility hohlraums D. C. Eder, A. E. Koniges, O. S. Jones, M. M. Marinak, M. T. Tobin, and B. J. MacGowan Lawrence Livermore National Laboratory, Livermore, CA 94551 Abstract The late-time (t ≥ 80 ns) behavior of hohlraums designed for the National Ignition Facility (NIF) is simulated using the multiphysics radiation hydrodynamics codes LASNEX and HYDRA. The spatial distribution of x-radiation outside the hohlraum is shown as a function of time. The energy spectrum of the x-ray emission is presented for various hohlraum viewing angles.
    [Show full text]
  • Fusion Power a Ten-Year Plan for American Energy Security
    Fusion Power A Ten-Year Plan for American Energy Security 1 Andrew Holland and Nick Cunningham BOARD OF DIRECTORS The Honorable Gary Hart, Chairman Admiral William Fallon, USN (Ret.) Senator Hart served the State of Colorado in the Admiral Fallon has led U.S. and Allied forces and U.S. Senate and was a member of the Committee played a leadership role in military and diplomatic on Armed Services during his tenure. matters at the highest levels of the U.S. government. Norman R. Augustine Raj Fernando Mr. Augustine was Chairman and Principal Raj Fernando is CEO and founder of RGY Officer of the American Red Cross for nine Chopper Trading, a technology based trading years and Chairman of the Council of the firm headquartered in Chicago. E National Academy of Engineering. The Hon. Donald Beyer Vice Admiral Lee Gunn, USN (Ret.) N The Hon. Donald Beyer is the former United Vice Admiral Gunn is the President of the States Ambassador to to Switzerland and Institute of Public Research at the CNA Liechtenstein, as well as a former Lieutenant Corporation, a non-profit corporation in Virginia. Governor and President of the Senate of Virginia. E The Hon. Jeffery Bleich Lieutenant General Claudia Kennedy, USA (Ret.) The Hon. Jeffery Bleich heads the Global Practice Lieutenant General Kennedy was the first woman for Munger, Tolles & Olson. He served as the U.S. to achieve the rank of three-star general in the Ambassador to Australia from 2009 to 2013. He United States Army. previously served in the Clinton Administration. General Lester L.
    [Show full text]
  • Introduction to Magnetic Fusion
    MIT Plasma Science & Fusion Center Introduction to Magnetic Fusion Dennis Whyte MIT Plasma Science and Fusion Center Nuclear Science and Engineering SULI, PPPL June 2015 Whyte, MFE, SULI 2015 1 Overview: Fusion Energy • Why? ! To meet growing world energy demands using a safe, clean method of producing electricity. • What? ! Extract net energy from controlled thermonuclear fusion of light elements • Who? ! International research teams of engineers and physicists. • Where? ! Research is worldwide ….eventual energy source has few geographical restrictions. • When? ! Many feasibility issues resolved….demonstration in next decades • How? ! This lecture Whyte, MFE, SULI 2015 2 Fusion & fission: binding energy, E = Δm c2 Whyte, MFE, SULI 2015 3 Thermonuclear fusion of hydrogen powers the universe: stars Whyte, MFE, SULI 2015 4 As a terrestrial energy source we are primarily interested in the exothermic fusion reactions of heavier hydrogenic isotopes and 3He • Hydrogenic species definitions: ! Hydrogen or p (M=1), Deuterium (M=2), Tritium (M=3) Whyte, MFE, SULI 2015 5 Exothermic fusion reactions of interest Net energy gain is distributed in the Kinetic energy of the fusion products Whyte, MFE, SULI 2015 6 D-T fusion facts d + t → α + n Q = 17.6 MeV 2 3 4 1 H + 1 H → 2 He + n Q = 17.6 MeV Conservation of energy & linear momentum when Ed,t<<Q mn 1 mα 4 Eα ! Q = QDT = 3.5 MeV En ! Q = QDT = 14.1 MeV mα + mn 5 mα + mn 5 Whyte, MFE, SULI 2015 7 A note about units • In nuclear engineering, nuclear science and plasmas we use the unit of electron-volt “eV” for both energy and temperature ! N.B.
    [Show full text]
  • Extreme Laser Pulses for Non-Thermal Fusion Ignition of Hydrogen–Boron for Clean and Cambridge.Org/Lpb Low-Cost Energy
    Laser and Particle Beams Extreme laser pulses for non-thermal fusion ignition of hydrogen–boron for clean and cambridge.org/lpb low-cost energy 1,2 3,4 5 6 6 Review Article Heinrich Hora , Shalom Eliezer , George H. Miley , JiaXiang Wang , YanXia Xu and Noaz Nissim3 Cite this article: Hora H, Eliezer S, Miley GH, Wang J, Xu Y, Nissim N (2018). Extreme laser 1University of New South Wales, Sydney 2052, Australia; 2HB11 Energy Pty. Ltd., Sydney, Australia; 3Soreq NRC, pulses for non-thermal fusion ignition of 4 5 – Yavne, Israel; Polytechnique University, Madrid, Spain; Department of Nuclear Plasma and Radiological hydrogen boron for clean and low-cost 6 energy. Laser and Particle Beams 36,335–340. Engineering, University of Illinois, Urbana IL, USA and State Key Laboratory of Precision Spectroscopy, https://doi.org/10.1017/S0263034618000289 Science Building A908a, East China Normal University, Shanghai 200062, China Received: 7 June 2018 Abstract Accepted: 17 July 2018 After achieving significant research results on laser-driven boron fusion, the essential facts are Key words: presented how the classical very low-energy gains of the initially known thermal ignition con- Clean energy; extreme power laser pulses; ditions for fusion of hydrogen (H) with the boron isotope 11 (HB11 fusion) were bridged by hydrogen–boron fusion; non-thermal fusion; plasma blocks nine orders of magnitudes in agreement with experiments. This is possible under extreme non-thermal equilibrium conditions for ignition by >10 PW-ps laser pulses of extreme Author for correspondence: power and nonlinear conditions. This low-temperature clean and low-cost fusion energy Heinrich Hora, University of New South Wales, generation is in crucial contrast to local thermal equilibrium conditions with the advantage Sydney 2052, Australia.
    [Show full text]
  • Laser Boron Fusion Reactor with Picosecond Petawatt Block Ignition
    Laser boron fusion reactor with picosecond petawatt block ignition Heinrich Hora1*, Shalom Eliezer2, Jiaxiang Wang3, Georg Korn4, Noaz Nissim2, Yanxia Xu3, Paraskevas Lalousis5, Götz Kirchhoff6 and George H. Miley7 1Department of Theoretical Physics, University of New South Wales, Sydney 2052, Australia 2SOREQ Research Centre, Yavne, Israel 3State Key Laboratory of Precision Spectroscopy, East China Normal University, Shanghai 200062, China 4ELI-Beam, Prague, Czech Republic 5Institute of Electronic Structure and Laser FORTH, Heraklion, Greece 6UJG Management GmbH, 85586 Poing, Germany 7Dept. Nuclear, Plasma & Radiol. Engineering, University of Illinois, Urbana IL, USA *[email protected] Abstract. Fusion of hydrogen with the boron Isotope 11, HB11 at local thermal equilibrium LTE, is 105 times more difficult than fusion of deuterium and tritium, DT. If - in contrast - extreme non-equilibrium plasma conditions are used with picoseconds laser pulses of more than 10PW power, the difficulties for fusion of HB11 change to the level of DT. This is based on a non-thermal transfer of laser energy into macroscopic plasma motion by nonlinear (ponderomotive) forces as theoretically predicted and experimentally confirmed as “ultrahigh acceleration”. Including elastic nuclear collisions of the alpha particles from HB11 reactions results in an avalanche process such that the energy gains 1 from HB11 fusion is nine orders of magnitudes above the classical values. In contrast to preceding laser fusion with spherical compression of the fuel, the side-on direct drive fusion of cylindrical uncompressed solid boron fuel trapped by magnetic fields above kilotesla, permits a reactor design with only one single laser beam for ignition within a spherical reactor.
    [Show full text]
  • X-Ray Emission from National Ignition Facility Indirect Drive Targets
    UCRL-JC-123557 X-Ray Emission from National Ignition Facility Indirect Drive Targets A. T. Anderson, R. A. Managan, M. T. Tobin, and P. F. Peterson AUG 1 6 1338 This paper was prepared for submittal to the American Nuclear Society 12th Topical Meeting on the Technology of Fusion Energy Reno, NV June 16-20,1996 This isapreprintofapaperintendedforpublicationina journal orproceedings. Since changes may be made before publication, this preprint is made available with the understanding that it will not be cited or reproduced without the permission of the author. DISTRIBUTION OF THIS DOCUMENT IS UNIMTED DISCLAIMER This document was prepared as an account of work sponsored by an agency of the United States Government Neither the United States Government nor the University of California nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise, does not necessarily constitute or imply its-endorsement, recommendation, or favoring by the United States Government or the University of California. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or the University of California, and shall not be used for advertising or product endorsement purposes. DISCLAIMER Portions of this document may be illegible in electronic image products. Images are produced from the best available origmal document.
    [Show full text]
  • Extreme Laser Pulses for Possible Development of Boron Fusion Power Reactors for Clean and Lasting Energy
    Extreme laser pulses for possible development of boron fusion power reactors for clean and lasting energy H. Hora*1, S. Eliezer2, G. J. Kirchhoff3, G.Korn4, P. Lalousis5, G. H. Miley6 and S. Moustaizis7 1Department of Theoretical Physics, University of New South Wales, Sydney 2052, Australia 2SOREQ Research Centre, Yavne, Israel 3UJG Management GmbH, 85586 Poing, Germany 4 ELI-Beam, Prague, Czech Republic. 5Institute of Electronic Structure and Lasers FORTH, Heraklion, Greece 6Dept. Nuclear, Plasma & Radiol. Engineering, University of Illinois, Urbana IL, USA 7Technical University Crete, Laboratory of Matter Structure and Laser Physics, Chania, Greece *[email protected] ABSTRACT Extreme laser pulses driving non-equilibrium processes in high density plasmas permit an increase of the fusion of hydrogen with the boron isotope 11 by nine orders of magnitude of the energy gains above the classical values. This is the result of initiating the reaction by non-thermal ultrahigh acceleration of plasma blocks by the nonlinear (ponderomotive) force of the laser field in addition to the avalanche reaction that has now been experimentally and theoretically manifested. The design of a very compact fusion power reactor is scheduled to produce then environmentally fully clean and inexhaustive generation of energy at profitably low costs. The reaction within a volume of cubic millimetres during a nanosecond can only be used for controlled power generation. Keywords: boron laser fusion, ultrahigh acceleration, ultrahigh magnetic fields, avalanche HB11 reaction, 1. INTRODUCTION The pollution of the atmosphere with carbon dioxide CO2 was early recognized in a profoundly precise way by Al Gore [1] – when beginning his leadership in this field – with warning into what catastrophe the climate change will go by threatening the whole mankind [2].
    [Show full text]
  • An Assessment of the Power Balance in Fusion Reactors
    AN ASSESSMENT OF THE POWER BALANCE IN FUSION REACTORS Masao Nozawa Don Steiner IGSSU OAK RIDGE NATIONAL LABORATORY OPERATED BY UNION CAJ^DE CORPORATION, • FOR THE U.S. ATOMIC ENERGY COMMISSION 0RNL-TM-M21 Contract No. W-7^05-eng-26 Thermonuclear Division AN ASSESSMENT OF THE POWER BALANCE IN FUSION REACTORS Masao Nozawa and Don Steiner [To "be submitted for publication in Nuclear Fusion] JANUARY 1974 OAK RIDGE NATIONAL LABORATORY Oak Ridge, Tennessee 37830 operated by UNION CARBIDE CORPORATION for the U.S. ATOMIC ENERGY COMMISSION -NOTICE- This report was prepared as an account of work sponsored by the United States Government. Neither the United States nor the United States Atomic Energy Commission, nor any of their employees, nor any of their contractors, subcontractors, or their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, com- pleteness or usefulness of any information, apparatus, product or process disclosed, or represents that its use would not infringe privately owned rights. set _ lEHfi fefe ill AN ASSESSMENT OF THE POWER BALANCE IN FUSION REACTORS* + Masao Nozawa and Don Steiner Oak Ridge National Laboratory, Oak Ridge, Tennessee 3T830 ABSTRACT A general formalism has been developed for analysis of the energy balance in fusion reactors. This formalism has been applied in a detailed and consistent fashion to four current D-T fusion reactor concepts, the laser fusion, the mirror, the thet.a pinch and the tokamak reactor concept. On the basis of a critical examination of the reactor subsystems, sets of reference parameters were adopted for each concept.
    [Show full text]