An Assessment of the Power Balance in Fusion Reactors
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Progress Towards Polar-Drive Ignition for the NIF
Home Search Collections Journals About Contact us My IOPscience Progress towards polar-drive ignition for the NIF This content has been downloaded from IOPscience. Please scroll down to see the full text. 2013 Nucl. Fusion 53 113021 (http://iopscience.iop.org/0029-5515/53/11/113021) View the table of contents for this issue, or go to the journal homepage for more Download details: IP Address: 198.125.179.18 This content was downloaded on 06/11/2013 at 22:08 Please note that terms and conditions apply. IOP PUBLISHING and INTERNATIONAL ATOMIC ENERGY AGENCY NUCLEAR FUSION Nucl. Fusion 53 (2013) 113021 (5pp) doi:10.1088/0029-5515/53/11/113021 Progress towards polar-drive ignition for the NIF R.L. McCrory1,a, R. Betti1,a, T.R. Boehly1, D.T. Casey2, T.J.B. Collins1, R.S. Craxton1, J.A. Delettrez1, D.H. Edgell1, R. Epstein1, J.A. Frenje2, D.H. Froula1, M. Gatu-Johnson2, V.Yu. Glebov1, V.N. Goncharov1, D.R. Harding1, M. Hohenberger1, S.X. Hu1, I.V. Igumenshchev1, T.J. Kessler1, J.P. Knauer1, C.K. Li2, J.A. Marozas1, F.J. Marshall1, P.W. McKenty1, D.D. Meyerhofer1,a, D.T. Michel1, J.F. Myatt1, P.M. Nilson1, S.J. Padalino3, R.D. Petrasso2, P.B. Radha1, S.P. Regan1, T.C. Sangster1, F.H. Seguin´ 2, W. Seka1, R.W. Short1, A. Shvydky1, S. Skupsky1, J.M. Soures1, C. Stoeckl1, W. Theobald1, B. Yaakobi1 and J.D. Zuegel1 1 Laboratory for Laser Energetics, University of Rochester, 250 East River Road, Rochester, NY 14623-1299, USA 2 Plasma Science Fusion Center, 173 Albany Street, Massachusetts Institute of Technology, Cambridge MA 02139, USA 3 Department of Physics, State University of New York at Geneseo, 1 College Circle, Geneseo NY 14454, USA E-mail: [email protected] Received 31 December 2012, accepted for publication 4 September 2013 Published 27 September 2013 Online at stacks.iop.org/NF/53/113021 Abstract The University of Rochester’s Laboratory for Laser Energetics (LLE) performs direct-drive inertial confinement fusion (ICF) research. -

"Nuclear Safety Info Center:Structural Mechanics in Reactor Technology
e YE i<D- *' . INTERIM REPORT Accession No. ORNL/FTR-678 Contract Program or Project Title: Nuclear Safety Information Center Subject of this Document: Structural Mechanics in Reactor Technology Type of Document: Trip Report Author (s): Wm. B. Cottrell Date of Document: September 6, 1979 Responsible NRC Individual and NRC Office or Division: Dr. G. L. Bennett Office of Nuclear Regulatory Research Division of Reactor Safety Research This document was prepared primarily for preliminary or internal use. It has not received full review and approval. Since there may be substantive changes, this document should not be consid- ered final. Prepared for U.S. Nuclear Regulatory Commission Washington, D. C. 20555 Under Interagency Agreements DOE 40-551-75 and 40-552-75 NRC FIN No. B0126 Oak Ridge National Laboratory Oak Ridge, Tennessee 37830 operated by Union Carbide Corporation for the Department of Energy INTERIM REPORT HC lesearcl anc "ec1nica IU33 i x Assistance Repor: ) y f u, yg . OAK RIDGE NATIONAL LABORATORY OPERATED SV UNION CARBIDE CORPORATION NUCLEe AR Dm510N _ = = ,.. ORNL FOREIGN TMP REPORT ORNL/FTR-678 DATE: September 6, 1979 SUBJECT: Report of Foreign Travel of Wm. B. Cottrell, Manager, Safety Information Section, Engineering Technology Division To: Herman Postma F R OM: Wm. B. Cottrell PURPOSE: To attend the 5th Int ( national Conference on Structural Mechanics in Reactor Technology, August 13-17, 1979, and the following seminar on " Assuring Structural Integrity of Steel Reactor Pressure Vessels, August 20-21, 1979; to visit Dr. H. Steel of the GDR State Office for Atomic Safety and Radiation Protection. SITE VISITED: The above conference and seminar were held at the Inter- national Congress Center in West Berlin; the Wednesday, August 15th, meeting was at the GDR State Office for Atomic Safety ..nd Radiation Protection in East Berlin. -

600 Technology (Applied Sciences)
600 600 Technology (Applied sciences) Class here inventions See also 303.48 for technology as a cause of cultural change; also 306.4 for sociology of technology; also 338.1–338.4 for economic aspects of industries based on specific technologies; also 338.9 for technology transfer, appropriate technology See Manual at 300 vs. 600; also at 363 vs. 302–307, 333.7, 570–590, 600; also at 363.1 vs. 600; also at 583–585 vs. 600 SUMMARY 601–609 Standard subdivisions and technical drawing, hazardous materials technology, patents 610 Medicine and health 620 Engineering and allied operations 630 Agriculture and related technologies 640 Home and family management 650 Management and auxiliary services 660 Chemical engineering and related technologies 670 Manufacturing 680 Manufacture of products for specific uses 690 Construction of buildings 601 Philosophy and theory 602 Miscellany Do not use for patents; class in 608 Class interdisciplinary works on trademarks and service marks in 929.9 Interdisciplinary collections of standards relocated to 389 .9 Commercial miscellany Class commercial miscellany of products and services used in individual and family living in 640.29; class commercial miscellany of manufactured products in 670.29; class interdisciplinary commercial miscellany in 381.029 603 Dictionaries, encyclopedias, concordances 604 Technical drawing, hazardous materials technology; groups of people 657 604 Dewey Decimal Classification 604 .2 Technical drawing Including arrangement and organization of drafting rooms, preservation and storage of drawings; specific drafting procedures and conventions (e.g., production illustration, dimensioning; lettering, titling; shades, shadows, projections); preparation and reading of copies Class here engineering graphics, mechanical drawing For architectural drawing, see 720.28. -

July/August 2004 Newsletter
Environmental Defense Institute News on Environmental Health and Safety Issues ")··..--~~~~~~~~~-,-~~~~~~--"--~~~ I July/August 2004 Volume 15 Number 3 Idaho Cancer Rates Continue to Rise at Record Levels According to the Cancer Data Registry ofldaho Dr. Thomas Pigford which was commissioned by the US there is a steady increase in Idaho cancer rates from the District Court hearing the Hanford Downwinders suit, beginning of data collection through 2002 (the latest both showed that causation for the high rate of cancer in report issued by the Registry). The 2000 report notes an the Northern Idaho Panhandle and Health District 3 increase of 3 59 cancer cases in recent years. "This was (Lewiston area) can be attributed to Hanford emissions one. of the largest single-year increases in cancer following wind patterns up the Columbia and Snake incidence in the history of the Cancer Data Registry of River drainage canyons. Idaho. Cancer sites with notable increases from 1999 to The Hanford· Downwinder litigation won two 2000 were lung, melanoma (in-situ), oral cavity and significant legal wins; 1.) the US 9th District Court of pharynx cancer counts increased over 1999 levels. The Appeals overruled the 1998 Spokane District Court number ofin-situ melanoma cases is 65% higher than for ruling by Judge McDonald that previously rejected the any previous year. The prostate cancer incidence rate is claims of most of the plaintiffs, and remanded the case the highest it has been since the spike in prostate cancer back to District Court for trial, based on Plaintiffs rates in 1990-1993 due to prostate-specific antigen scientific briefs showing significantly more particulate screening. -

Nuclear Propulsion
16 Nuclear Propulsion Claudio Bruno DIMA, University of Rome (La Sapienza), Roma Italy 1. Introduction Nuclear propulsion (NP) concepts go back to the very end of WW II. Scientists informed about the effects of the US atomic bomb thought of exploiting its energy release for applications like commercial electric power generation, but also rockets and space flight [Shepherd and Cleaver, 1948, 1949; Bussard and DeLauer, 1958]. However, space flight was still considered science fiction, and the military had to deal with more concrete things, like the Cold War. Thus, besides power generation, second stages of ICBM, submarine propulsion, long range and long duration airplanes and missiles became the focus of nuclear energy applications. It was the second-stage and airplane application that drove R&D in nuclear propulsion. With the advent of reliable ICBM (the Atlas missile) and lighter fission and thermonuclear warheads, a nuclear-powered second stage became no longer necessary. Airplane applications were found impractical: the Convair NB-36 required such a heavy lead shield for the crew that testing and operation were much restricted. Nuclear-powered missiles were easier to design, e.g., project PLUTO, but still far more complicated compared to conventional. The Soviets investigated airplanes and rockets powered by nuclear power as well, and discarded them too. The history of NP can be found in [Czysz and Bruno, 2009, Chapter 7; Lawrence, 2008; Lawrence et al, 1995; Gunn and Ehresman, 2003; Dewar, 2004] and will not be reported here. Basic technology is also discussed in the references above, in particular reactor design is in [Lawrence et al, 1995]. -

Fusion Ignition Via a Magnetically-Assisted Fast Ignition Approach
Fusion ignition via a magnetically-assisted fast ignition approach W.-M. Wang1,3*, P. Gibbon2,4†, Z.-M. Sheng3,5,6‡, Y. T. Li1,3, and J. Zhang3,6 1Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, CAS, Beijing 100190, China 2Forschungszentrum Jülich GmbH, Institute for Advanced Simulation, Jülich Supercomputing Centre, D-52425 Jülich, Germany 3Collaborative Innovation Center of IFSA, Shanghai Jiao Tong University, Shanghai 200240, China 4Centre for Mathematical Plasma Astrophysics, Katholieke Universiteit Leuven, 3000 Leuven, Belgium 5SUPA, Department of Physics, University of Strathclyde, Glasgow G4 0NG, United Kingdom 6Key Laboratory for Laser Plasmas (MoE) and Department of Physics and Astronomy, Shanghai Jiao Tong University, Shanghai 200240, China * E-mail: [email protected] † E-mail: [email protected] ‡ E-mail: [email protected] 1 Significant progress has been made towards laser-driven fusion ignition via different schemes, including direct and indirect central ignition, fast ignition, shock ignition, and impact ignition schemes. However, to reach ignition conditions, there are still various technical and physical challenges to be solved for all these schemes. Here, our multi-dimensional integrated simulation shows that the fast-ignition conditions could be achieved when two 2.8 petawatt heating laser pulses counter-propagate along a 3.5 kilotesla external magnetic field. Within a period of 5 picoseconds, the laser pulses heat a nuclear fuel to reach the ignition conditions. Furthermore, we present the parameter windows of lasers and magnetic fields required for ignition for experimental test. To achieve controlled nuclear fusion energy, the central ignition concept of inertial confinement fusion (ICF) was proposed in 1970s [1-4]. -

Fact Sheet on U.S. Nuclear Powered Warship (NPW) Safety
Fact Sheet on U.S. Nuclear Powered Warship (NPW) Safety 1. Commitments of the U.S. Government about the Safety of U.S. NPWs U.S. Nuclear Powered Warships (NPWs) have safely operated for more than 50 years without experiencing any reactor accident or any release of radioactivity that hurt human health or had an adverse effect on marine life. Naval reactors have an outstanding record of over 134 million miles safely steamed on nuclear power, and they have amassed over 5700 reactor-years of safe operation. Currently, the U.S. has 83 nuclear-powered ships: 72 submarines, 10 aircraft carriers and one research vessel. These NPWs make up about forty percent of major U.S. naval combatants, and they visit over 150 ports in over 50 countries, including approximately 70 ports in the U.S. and three in Japan. Regarding the safety of NPWs visiting Japanese ports, the U.S. Government has made firm commitments including those in the Aide-Memoire of 1964; the Statement by the U.S. Government on Operation of Nuclear Powered Warships in Foreign Ports of 1964; the Aide-Memoire of 1967; and the Memorandum of Conversation of 1968. Since 1964 U.S. NPWs have visited Japanese ports (i.e., Yokosuka, Sasebo and White Beach) more than 1200 times. The results of monitoring in these ports conducted by the Government of Japan and the U.S. Government, respectively, demonstrate that the operation of U.S. NPWs does not result in any increase in the general background radioactivity of the environment. The U.S. Government states that every single aspect of these commitments continues to be firmly in place. -

ORNL Review Dorothy M
Oak Ridge National Laboratory VOLUME 11, NUMBER 2 SPRING 1978 2 State of the Laboratory-1977 - A Longer-Range View By HERMAN POSTMA THE COVER PHOTOS: Director Herman Postma, on the cover, and Henry Inouye, opposite page, take turns peering into an environmental test chamber in which new Long Range Ordered Alloys will be tested later this year. The tests will demonstrate the alloys' increased strength with main 22 How Deep Is the Burn? tenance of ductility at temperatures up to By JEFF McKENNA 950°C. This is one of the metallurgical achievements at the Laboratory in 1977 described by Postma in the State of the Laboratory address he delivered early this year. 30 Stopping Biological Time Editor By CAROLYN KRAUSE BARBARA LYON Staff Writer CAROLYN KRAUSE Consulting Editor 46 Regional Impacts of the Energy Plan ALEX ZUCKER Art Director BILL CLARK Publication taff: Technical Editing/ DEPARTMENTS LaRue Foster; Typography/ Betty Little ton; Makeup/ Betty Jo Williams; Repro Take a Number 21 duction/ Bill West Awards and Appointments 28 Letters 38 Information Meeting Highlights 39 Books 45 The Review is published quarterly and distributed to employees and others asso ciated with the Oak Ridge National Lab oratory. The editorial office is in Building 4500-North, Oak Ridge National Labora tory, P.O. Box X, Oak Ridge, Tennessee 37830. Telephone: (615) 483-8611 , Exten OAK RIDGE NATIONAL LABORATORY sion 3-6900 (J.<'TS 850-6900). OPERATED BY UN ION CARBIDE CORPORAT ION • FOR THE DEPARTMEN T OF ENERGY :ritv/-- state of the Laboratory-1977 -A Longer-Range View By Herman Postma hile the State of the Labora This year I not only will review with respect to energy-particu W tory address itself is a tra what has characterized ORNL in larly during this year with respect dition at ORNL, there is little in 1977, but also will place it in the to nuclear energy. -
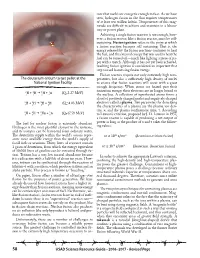
USAD Science Resource Guide • 2016–2017 • Revised Page The
sure that nuclei are energetic enough to fuse. As we have seen, hydrogen fusion in the Sun requires temperatures of at least ten million kelvin. Temperatures of this mag- nitude are difficult to achieve and maintain in a labora- tory or power plant. Achieving a single fusion reaction is not enough, how- ever; a fusion reactor, like a fission reactor, must be self- sustaining. Fusion ignition refers to the point at which a fusion reaction becomes self-sustaining. That is, the energy released by the fusion reactions continues to heat the fuel, and the external energy that was used to heat the fuel can be turned off—much like lighting a piece of pa- per with a match. Although it has not yet been achieved, reaching fusion ignition is considered an important first step toward harnessing fusion energy. The deuterium-tritium target pellet at the Fusion reactors require not only extremely high tem- peratures, but also a sufficiently high density of nuclei National Ignition Facility. to ensure that fusion reactions will occur with a great enough frequency. When atoms are heated past their 2H + 2H 3H + 1n ionization energy, their electrons are no longer bound to 1 1 2 0 (Q=3.27 MeV) the nucleus. A collection of superheated atoms forms a cloud of positively charged nuclei and negatively charged 2H + 2 H 3 H + 1 H 1 1 1 1 (Q=4.03 MeV) electrons called a plasma. Two parameters for describing the characteristics of a plasma are the plasma ion den- τ 2H + 3H 4He + 1n sity, n, and the plasma confinement time, . -

The Nuclear Non-Proliferation Treaty's Obligation to Transfer Peaceful Nuclear Energy Technology: One Proposal of a Technology
Fordham International Law Journal Volume 19, Issue 5 1995 Article 11 The Nuclear Non-Proliferation Treaty’s Obligation to Transfer Peaceful Nuclear Energy Technology: One Proposal of a Technology Seth Grae∗ ∗ Copyright c 1995 by the authors. Fordham International Law Journal is produced by The Berke- ley Electronic Press (bepress). http://ir.lawnet.fordham.edu/ilj The Nuclear Non-Proliferation Treaty’s Obligation to Transfer Peaceful Nuclear Energy Technology: One Proposal of a Technology Seth Grae Abstract This Essay discusses the technology transfer provisions of the Treaty on the Non-Proliferation of Nuclear Weapons (“NPT”) and describes the Radkowsky Thorium Reactor, which is being developed as a peaceful nuclear energy technology. THE NUCLEAR NON-PROLIFERATION TREATY'S OBLIGATION TO TRANSFER PEACEFUL NUCLEAR ENERGY TECHNOLOGY: ONE PROPOSAL OF A TECHNOLOGY Seth Grae* INTRODUCTION The Treaty on the Non-Proliferaticn of Nuclear Weapons ("NPT")1 is the main document in the international effort to stop the proliferation of nuclear weapons. As stated in the pre- amble of the NPT, "proliferation of nuclear weapons would seri- ously enhance the danger of nuclear war," and devastation "would be visited upon all mankind by a nuclear war."' The NPT calls for a halt to proliferation of nuclear weapons and tech- nology and also calls for the transfer of "peaceful" nuclear en- ergy technology. This Essay discusses the technology transfer provisions of the NPT and describes the Radkowsky Thorium Re- actor, which is being developed as a peaceful nuclear energy technology. I. BACKGROUND TO THE RADKOWSKY THORIUM REACTOR A. The Treaty on the Non-Proliferationof Nuclear Weapons Obligation to Transfer Peaceful Nuclear Energy Technology Article IV(1) of the NPT asserts that parties to the NPT have an "inalienable right" to develop, research, produce, and use nu- clear energy for peaceful purposes. -

Road Map to Clean Energy Using Laser Beam Ignition of Boron-Hydrogen Fusion
Laser and Particle Beams (2017), 35, 730–740. © Cambridge University Press, 2017 0263-0346/17 doi:10.1017/S0263034617000799 Road map to clean energy using laser beam ignition of boron-hydrogen fusion H. HORA,1 S. ELIEZER,2,4 G.J. KIRCHHOFF,3 N. NISSIM,2,5 J.X. WANG,6 P. LALOUSIS,7 Y.X. XU,6 8 4 9 9 G.H. MILEY, J.M. MARTINEZ-VAL, W. MCKENZIE, AND J. KIRCHHOFF 1Department of Theoretical Physics, University of New South Wales, Sydney 2052, Australia 2SOREQ Research Centre, Yavne, Israel 3UJG Management GmbH, 85586 Poing, Germany 4Polytechnique University, Madrid, Spain 5Department of Earth and Planetary Science, University of California, Berkeley, CA 94720, USA 6State Key Laboratory of Precision Spectroscopy, East China Normal University, Shanghai 200062, China 7Institute of Electronic Structure and Laser FORTH, Heraklion, Greece 8Department Nuclear, Plasma & Radiol. Engineering, University of Illinois, Urbana IL, USA 9HB11 Energy Pty. Ltd., Sydney, Australia (RECEIVED 26 September 2017; ACCEPTED 16 October 2017) Abstract With the aim to overcome the problems of climatic changes and rising ocean levels, one option is to produce large-scale sustainable energy by nuclear fusion of hydrogen and other very light nuclei similar to the energy source of the sun. Sixty years of worldwide research for the ignition of the heavy hydrogen isotopes deuterium (D) and tritium (T) have come close to a breakthrough for ignition. The problem with the DT fusion is that generated neutrons are producing radioactive waste. One exception as the ideal clean fusion process – without neutron production – is the fusion of hydrogen (H) with the boron isotope 11B11 (B11). -

NAVY Safety & Occupational Health Manual OPNAV M-5100.23 of 5 Jun
OPNAV M-5100.23 5 Jun 2020 NAVY SAFETY AND OCCUPATIONAL HEALTH MANUAL THIS PAGE INTENTIONALLY LEFT BLANK THIS PAGE INTENTIONALLY LEFT BLANK OPNAV M-5100.23 5 Jun 2020 TABLE OF CONTENTS SECTION A. SAFETY MANAGEMENT SYSTEM Chapter 1. INTRODUCTION A0101. Purpose……………………………………………………………………..... A1-2 A0102. Scope and Applicability……………………………………………………… A1-2 A0103. Definition of Terms………………………………………………………….. A1-4 A0104. Background…………………………………………………………………... A1-4 A0105. Discussion……………………………………………………………………. A1-5 A0106. Introduction to the Navy SMS Framework………………………………….. A1-6 A0107. Responsibilities………………………………………………………………. A1-7 Chapter 2. POLICY AND ORGANIZATIONAL COMMITMENT A0201. Introduction………………………………………………………………….. A2-1 A0202. Methodology………………………………………………………………… A2-1 A0203. Organizational Commitment and Accountability…………………………… A2-3 A0204. Appointment of SMS Personnel……………………………………………… A2-4 Chapter 3. RISK MANAGEMENT A0301. Introduction………………………………………………………………….. A3-1 A0302. Methodology………………………………………………………………… A3-1 A0303. Error Tolerance……………………………………………………………… A3-1 A0304. Principles…………………………………………………………………..... A3-2 A0305. Requirements………………………………………………………………… A3-3 Chapter 4. ASSURANCE A0401. Introduction………………………………………………………………….. A4-1 A0402. Methodology………………………………………………………………… A4-1 A0403. Requirements……………………………………………………..................... A4-1 A0404. Continuous Improvement………………………………………………….… A4-2 A0405. Management Review……………………………………………………….... A4-2 Chapter 5. PROMOTION A0501. Introduction………………………………………………………………….. A5-1