DOCSLIB.ORG

Introduction to Magnetic Fusion

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

MIT Plasma Science & Fusion Center Introduction to Magnetic Fusion Dennis Whyte MIT Plasma Science and Fusion Center Nuclear Science and Engineering SULI, PPPL June 2015 Whyte, MFE, SULI 2015 1 Overview: Fusion Energy • Why? ! To meet growing world energy demands using a safe, clean method of producing electricity. • What? ! Extract net energy from controlled thermonuclear fusion of light elements • Who? ! International research teams of engineers and physicists. • Where? ! Research is worldwide ….eventual energy source has few geographical restrictions. • When? ! Many feasibility issues resolved….demonstration in next decades • How? ! This lecture Whyte, MFE, SULI 2015 2 Fusion & fission: binding energy, E = Δm c2 Whyte, MFE, SULI 2015 3 Thermonuclear fusion of hydrogen powers the universe: stars Whyte, MFE, SULI 2015 4 As a terrestrial energy source we are primarily interested in the exothermic fusion reactions of heavier hydrogenic isotopes and 3He • Hydrogenic species definitions: ! Hydrogen or p (M=1), Deuterium (M=2), Tritium (M=3) Whyte, MFE, SULI 2015 5 Exothermic fusion reactions of interest Net energy gain is distributed in the Kinetic energy of the fusion products Whyte, MFE, SULI 2015 6 D-T fusion facts d + t → α + n Q = 17.6 MeV 2 3 4 1 H + 1 H → 2 He + n Q = 17.6 MeV Conservation of energy & linear momentum when Ed,t<<Q mn 1 mα 4 Eα ! Q = QDT = 3.5 MeV En ! Q = QDT = 14.1 MeV mα + mn 5 mα + mn 5 Whyte, MFE, SULI 2015 7 A note about units • In nuclear engineering, nuclear science and plasmas we use the unit of electron-volt “eV” for both energy and temperature ! N.B. Energy and temperature are NOT the same thing! • The eV, rather than Joules, is the natural energy unit when dealing with elementary particles: Energy gained by a particle with unit electron charge falling through 1 Volt of electrostatic potential energy…that’s natural? • Yes! E.g. Electrostatic particle accelerator, beam of protons fall through potential drop of 1 MV x 1 Ampere current. Beam power: V x I =1 MW..so what is the energy per proton? 106 eV! e ⎛ C ⎞ 6 I ⎛ proton ⎞ 6 6 J i I ⎜ ⎟ i10 V = ⎜ ⎟ i10 e V = 10 e ⎝ s ⎠ e ⎝ s ⎠ s Whyte, MFE, SULI 2015 8 Handy dandy unit conversions & ! Typical physical parameters • 1 eV = 1.6 x 10-19 J (conversion between single particle & SI) • 1 e = 1.6 x 10 -19 C • 1 eV ~ 11600 Kelvin ~ 104 K (describing temperatures) • 10 keV ~ 108 K ~ 100 million K (typical fusion T)! 4 1/2 • vth ~ 10 (T / M) m/s {T in eV, M in amu} ! At typical fusion temperature thermal velocity of protons ~ 106 m/s • 1 barn = 10-28 m2 = 10-24 m2 (nuclear cross section) Whyte, MFE, SULI 2015 9 We also use eV to describe mass ! through energy-mass equivalence • E = m c2 " m = E / c2 • Electron: 0.511 MeV / c2 • Atomic mass unit ~ proton ~ neutron: 970 MeV / c2 ~ 103 MeV • So note D-T fusion gain: ~ 20 MeV arises from relative decrease in rest mass energies of products compared to reactants! ~ 20 MeV / (5x1000 MeV) ~ 0.4% Whyte, MFE, SULI 2015 10 Fusion is a nuclear reaction…it occurs due to the strong nuclear force • Fundamental competition: nuclear binding force vs. repulsive Coulomb force for the like + charged nuclei. U rnucleus Potential ! repulsive diagram for Coulomb force Interacting! nuclei If the nuclei get Close enough r Together (~ nuclei radius)! Distance of separation then the binding nuclear force Dominates --> fusion attracting nuclear force Whyte, MFE, SULI 2015 11 The Coulomb repulsion must be overcome with very high particle energies • Repulsive force acting on two U particles with same charge (ions), rnucleus 2 repulsive Z Z e Z Z e Coulomb force U[J] = 1 2 [J] → U[eV ] = 1 2 4πε0r 4πε0r r attracting Z Z nuclear force U[eV ] = 1.4[eV i nm] 1 2 r [nm] -6 Z=1 " rnucleus ~ 4 fm = 4x10 nm " U ~ 350,000 eV Compare to average atom energy at room temperature Ethermal ~ 300 K ~ 0.03 eV ! Whyte, MFE, SULI 2015 12 Despite Ucoulomb~350 keV, ! we can obtain D-T fusion at T~10 keV • Three important effects allow this:! 1. Quantum-mechanical tunneling (wave-particle nature of the interacting nuclei_ provides finite probability for energies below Ucoulomb! 2. Large low-energy nuclear resonance for d-t 3. Fusion achieved in thermalized population distribution with significant population at E > T Whyte, MFE, SULI 2015 13 Fusion cross-sections: Peak of D-T reaction at 0.06 MeV " x 300 energy gain! http://www.psfc.mit.edu/research/MFEFormulary/ Whyte, MFE, SULI 2015 14 Cross-section has units of area but is actually an expression of normalized probability of a reaction occurring per target particle Linear reaction coefficient in homogenous medium dP µ [m−1] ≡ d−t dx µ [m−1] m2 d−t σ ⎣⎡ ⎦⎤ ≡ 3 ntarget[#/ m ] For nuclear reactions, nuclei typically must approach to nuclear distances for strong-force to come into play. Thus “cross-section” -14 2 -28 2 of (rnuclesu ~10 m) ~ 10 m = 1 barn is quite large… Whyte, MFE, SULI 2015 15 Fusion cross-sections: Peak of D-T reaction at 0.06 MeV " x 300 energy gain! Whyte, MFE, SULI 2015 16 Major conceptual challenge #1:! Nuclei have much higher probability of undergoing non-fusion Coulomb collisions ) 2 Cross-section (m Whyte, MFE, SULI 2015 17 Major conceptual challenge #1:! Nuclei have much higher probability of undergoing non-fusion Coulomb collisions Coulomb collision occurs “at distance”, unlike nuclear reactions By carefully integrating over appropriate impact parameters MeV ions are dominated by energy loss to electrons in matter This “competes” against fusion reactions because it removes energy of needed fast particles Whyte, MFE, SULI 2015 18 Fusion is easy, produced all the time in accelerator labs. Fusion energy is hard because it requires thermalized population • Let’s try to make a fusion energy reactor by producing a 1 MeV beam of deuterons streaming into a tritium target • Mass density solid hydrogen ! ~ 0.1 g/cm3 • From previous graph: Stopping power for the deuteron! S ~ 103 MeV cm2/g " S ! ~ 102 MeV / cm! • Distance 1 MeV deuteron travels in solid tritium before coming to rest due to slowing down by Coulomb collisions ! 2 -2 E0 / (S !) ~ 1 MeV / 10 MeV / cm ~ 10 cm (100 microns) • Probability of fusion reaction? Average cross-section ~ 2 barn (generous!) = 2 x 10-24 cm2 continued on next slide Whyte, MFE, SULI 2015 19 Fusion is easy, produced all the time in accelerator labs. Fusion energy is hard because it requires thermalized population -3 • n ~ ! NA / A = 0.1 * 6e23 / 1 = 6e22 cm : this is the volumetric number density of tritons in target • Probability of fusion per unit distance in tritium target! = 2x10-24 cm2 * 6e22 cm-3 = 0.1 fusion reactions / cm-1 • Approximate probability that ion fuses before full stopping:! 0.1 cm-1 * 10-2 cm ~ 10-3 (oh man that doesn’t sound good) ! Note this probability is independent of the target number density.! • Power balance?! - Power supplied by you: 1 MeV / particle - Power gained from fusion: ! ~20 MeV / fusion * 10-3 fusion/ particle ~ 0.02 MeV/particle Whyte, MFE, SULI 2015 20 Thermonuclear fusion is necessary! Coulomb collisions in thermalized population Interior of sun ~ 15 MK Fusion energy needs confinement Needs Temperature ASSURES FUSION ENERGY MUST BE IN PLASMA STATE Whyte, MFE, SULI 2015 21 Major conceptual challenge #2:! There are no natural sources of tritium -4 • Deuterium is so abundant on earth…fD/H ~ 1.5x10 … as to make an essentially infinite fuel supply for fusion. ! Think of the # water molecules in the ocean!! • But tritium does not occur naturally due to its short half-life, ! T " 3He + e- 1/2 life = 12.3 years.! • So Tritium must be bred. How? ! D + n --> T + (e.g. CANDU fission reactor) ! This is the present “seed” source for fusion tritium amounting to ~20 kg Whyte, MFE, SULI 2015 22 Major conceptual challenge #2:! Fusion must be a breeder reactor • For fusion we have another important set of nuclear reactions involving the neutron product from the D-T fusion reaction and lithium that can produce tritium.! 6Li + n " T + 4He + 4.8 MeV! 7Li + n " T + 4He + n - 2.3 MeV • Lithium is highly abundant: 93% Li-7, 7% Li-6 Whyte, MFE, SULI 2015 23 Major conceptual challenge #2:! Fusion energy system is a very simple breeder reactor d + t → α + n Q = 17.6 MeV n + 6 Li → t +α Q = 4.8 MeV d + 6 Li → 2α Q = 22.4 MeV Whyte, MFE, SULI 2015 24 A fusion energy device heats itself and recycles neutrons internally for tritium hydrogen fuel Energy Before (MeV) Energy After (MeV) ~ 0.01 14.1 ~0.01 3.5 Plasma physics: T=10 keV Whyte, MFE, SULI 2015 25 A fusion energy device heats itself and recycles neutrons internally for tritium hydrogen fuel Energy Before Energy After ~0.01 14.1 + 3.5 ~0.01 + Plasma physics, MAlfven >1 Alphas heat plasma through scattering Whyte, MFE, SULI 2015 26 A fusion energy device heats itself and recycles neutrons internally for tritium hydrogen fuel Escapes plasma 14.1 MeV Nuclear Physics + + Whyte, MFE, SULI 2015 27 A fusion energy device heats itself and recycles neutrons internally for tritium hydrogen fuel 14.1 " 0 + Heat + Nuclear Engineering Electricity Whyte, MFE, SULI 2015 28 A fusion energy device heats itself and recycles neutrons internally for tritium hydrogen fuel 6-Li + n " He + T + + Nuclear Engineering, Radiochemistry Whyte, MFE, SULI 2015 29 A fusion energy device heats itself and recycles neutrons internally for tritium hydrogen fuel Surrounding materials Nuclear Material Science sheath + + Low-T Plasma Material Science Whyte, MFE, SULI 2015 30 The lure of fusion • Nearly limitless fuel:! Deuterium + Lithium-6 ! 2 Helium-4 + 22 MeV • No radioactive waste in fuel cycle • Million times power density of “chemical” energy ! Minimal fuel / waste stream ! Minimized environmental footprint • Inherently safe because it requires T > 5 keV Whyte, MFE, SULI 2015 31 The basic idea of electricity generation from fusion • For electricity generation we absorb the power of the fusion reactants in a “blanket” and use this heating to run a turbine/ generator cycle.! • Tricky bit? ! The fusion core.
Recommended publications
  • Progress Towards Polar-Drive Ignition for the NIF

    Progress Towards Polar-Drive Ignition for the NIF

    Home Search Collections Journals About Contact us My IOPscience Progress towards polar-drive ignition for the NIF This content has been downloaded from IOPscience. Please scroll down to see the full text. 2013 Nucl. Fusion 53 113021 (http://iopscience.iop.org/0029-5515/53/11/113021) View the table of contents for this issue, or go to the journal homepage for more Download details: IP Address: 198.125.179.18 This content was downloaded on 06/11/2013 at 22:08 Please note that terms and conditions apply. IOP PUBLISHING and INTERNATIONAL ATOMIC ENERGY AGENCY NUCLEAR FUSION Nucl. Fusion 53 (2013) 113021 (5pp) doi:10.1088/0029-5515/53/11/113021 Progress towards polar-drive ignition for the NIF R.L. McCrory1,a, R. Betti1,a, T.R. Boehly1, D.T. Casey2, T.J.B. Collins1, R.S. Craxton1, J.A. Delettrez1, D.H. Edgell1, R. Epstein1, J.A. Frenje2, D.H. Froula1, M. Gatu-Johnson2, V.Yu. Glebov1, V.N. Goncharov1, D.R. Harding1, M. Hohenberger1, S.X. Hu1, I.V. Igumenshchev1, T.J. Kessler1, J.P. Knauer1, C.K. Li2, J.A. Marozas1, F.J. Marshall1, P.W. McKenty1, D.D. Meyerhofer1,a, D.T. Michel1, J.F. Myatt1, P.M. Nilson1, S.J. Padalino3, R.D. Petrasso2, P.B. Radha1, S.P. Regan1, T.C. Sangster1, F.H. Seguin´ 2, W. Seka1, R.W. Short1, A. Shvydky1, S. Skupsky1, J.M. Soures1, C. Stoeckl1, W. Theobald1, B. Yaakobi1 and J.D. Zuegel1 1 Laboratory for Laser Energetics, University of Rochester, 250 East River Road, Rochester, NY 14623-1299, USA 2 Plasma Science Fusion Center, 173 Albany Street, Massachusetts Institute of Technology, Cambridge MA 02139, USA 3 Department of Physics, State University of New York at Geneseo, 1 College Circle, Geneseo NY 14454, USA E-mail: [email protected] Received 31 December 2012, accepted for publication 4 September 2013 Published 27 September 2013 Online at stacks.iop.org/NF/53/113021 Abstract The University of Rochester’s Laboratory for Laser Energetics (LLE) performs direct-drive inertial confinement fusion (ICF) research.
  • Thermonuclear AB-Reactors for Aerospace

    Thermonuclear AB-Reactors for Aerospace

    1 Article Micro Thermonuclear Reactor after Ct 9 18 06 AIAA-2006-8104 Micro -Thermonuclear AB-Reactors for Aerospace* Alexander Bolonkin C&R, 1310 Avenue R, #F-6, Brooklyn, NY 11229, USA T/F 718-339-4563, [email protected], [email protected], http://Bolonkin.narod.ru Abstract About fifty years ago, scientists conducted R&D of a thermonuclear reactor that promises a true revolution in the energy industry and, especially, in aerospace. Using such a reactor, aircraft could undertake flights of very long distance and for extended periods and that, of course, decreases a significant cost of aerial transportation, allowing the saving of ever-more expensive imported oil-based fuels. (As of mid-2006, the USA’s DoD has a program to make aircraft fuel from domestic natural gas sources.) The temperature and pressure required for any particular fuel to fuse is known as the Lawson criterion L. Lawson criterion relates to plasma production temperature, plasma density and time. The thermonuclear reaction is realised when L > 1014. There are two main methods of nuclear fusion: inertial confinement fusion (ICF) and magnetic confinement fusion (MCF). Existing thermonuclear reactors are very complex, expensive, large, and heavy. They cannot achieve the Lawson criterion. The author offers several innovations that he first suggested publicly early in 1983 for the AB multi- reflex engine, space propulsion, getting energy from plasma, etc. (see: A. Bolonkin, Non-Rocket Space Launch and Flight, Elsevier, London, 2006, Chapters 12, 3A). It is the micro-thermonuclear AB- Reactors. That is new micro-thermonuclear reactor with very small fuel pellet that uses plasma confinement generated by multi-reflection of laser beam or its own magnetic field.
  • Article Thermonuclear Bomb 5 7 12

    Article Thermonuclear Bomb 5 7 12

    1 Inexpensive Mini Thermonuclear Reactor By Alexander Bolonkin [email protected] New York, April 2012 2 Article Thermonuclear Reactor 1 26 13 Inexpensive Mini Thermonuclear Reactor By Alexander Bolonkin C&R Co., [email protected] Abstract This proposed design for a mini thermonuclear reactor uses a method based upon a series of important innovations. A cumulative explosion presses a capsule with nuclear fuel up to 100 thousands of atmospheres, the explosive electric generator heats the capsule/pellet up to 100 million degrees and a special capsule and a special cover which keeps these pressure and temperature in capsule up to 0.001 sec. which is sufficient for Lawson criteria for ignition of thermonuclear fuel. Major advantages of these reactors/bombs is its very low cost, dimension, weight and easy production, which does not require a complex industry. The mini thermonuclear bomb can be delivered as a shell by conventional gun (from 155 mm), small civil aircraft, boat or even by an individual. The same method may be used for thermonuclear engine for electric energy plants, ships, aircrafts, tracks and rockets. ----------------------------------------------------------------------- Key words: Thermonuclear mini bomb, thermonuclear reactor, nuclear energy, nuclear engine, nuclear space propulsion. Introduction It is common knowledge that thermonuclear bombs are extremely powerful but very expensive and difficult to produce as it requires a conventional nuclear bomb for ignition. In stark contrast, the Mini Thermonuclear Bomb is very inexpensive. Moreover, in contrast to conventional dangerous radioactive or neutron bombs which generates enormous power, the Mini Thermonuclear Bomb does not have gamma or neutron radiation which, in effect, makes it a ―clean‖ bomb having only the flash and shock wave of a conventional explosive but much more powerful (from 1 ton of TNT and more, for example 100 tons).
  • Cumulative List of INFUSE Awards

    Cumulative List of INFUSE Awards

    Cumulative List of INFUSE Awards INFUSE 2021a, June 14, 2021 Company: Air Squared, Inc., DUNS: 824841027 Title: Design, test, and evaluation of a scroll roughing vacuum pump with filter and Vespel tip seals for tritium handling Abstract: Development of a novel scroll pump that meets the strict containment levels of D/T experimental campaigns aiming to replace both the scroll and metal bellows pumps with a single scroll pump utilizing Vespel tip seals to demonstrate improved reliability, discharge pressure, and reduced costs. Co. PI: Mr. John Wilson Co. e-mail: [email protected] Laboratory: ORNL Lab PI: Mr. Charles Smith III, [email protected] Cumulative List of INFUSE Awards INFUSE 2021a, June 14, 2021 Company: Commonwealth Fusion Systems, DUNS: 117005109 Title: Informing Layout and Performance Requirements for SPARC Massive Gas Injection Abstract: Commonwealth Fusion Systems (CFS) is designing a compact tokamak called SPARC and is evaluating massive gas injection (MGI) as its primary means of plasma disruption mitigation technique. Present conservative scoping has enabled a preliminary design of the MGI system. However, physics-based modeling can help CFS inform an optimized layout, which can either reduce the cost of MGI system by reducing the number of gas injectors or provide supporting evidence that present scoping estimates are correct. This program leverages the 3D magneto-hydrodynamic modeling expertise at Princeton Plasma Physics Laboratory (PPPL), which is maintained through the development and use of the M3D-C1 code. CFS and PPPL will develop a gas source model representative of SPARC MGI’s system. PPPL would then use M3D- C1 to simulate unmitigated SPARC disruptions, to develop a baseline response, and then simulate mitigated disruptions representing a variety of MGI system configurations.
  • Fusion Ignition Via a Magnetically-Assisted Fast Ignition Approach

    Fusion Ignition Via a Magnetically-Assisted Fast Ignition Approach

    Fusion ignition via a magnetically-assisted fast ignition approach W.-M. Wang1,3*, P. Gibbon2,4†, Z.-M. Sheng3,5,6‡, Y. T. Li1,3, and J. Zhang3,6 1Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, CAS, Beijing 100190, China 2Forschungszentrum Jülich GmbH, Institute for Advanced Simulation, Jülich Supercomputing Centre, D-52425 Jülich, Germany 3Collaborative Innovation Center of IFSA, Shanghai Jiao Tong University, Shanghai 200240, China 4Centre for Mathematical Plasma Astrophysics, Katholieke Universiteit Leuven, 3000 Leuven, Belgium 5SUPA, Department of Physics, University of Strathclyde, Glasgow G4 0NG, United Kingdom 6Key Laboratory for Laser Plasmas (MoE) and Department of Physics and Astronomy, Shanghai Jiao Tong University, Shanghai 200240, China * E-mail: [email protected] † E-mail: [email protected] ‡ E-mail: [email protected] 1 Significant progress has been made towards laser-driven fusion ignition via different schemes, including direct and indirect central ignition, fast ignition, shock ignition, and impact ignition schemes. However, to reach ignition conditions, there are still various technical and physical challenges to be solved for all these schemes. Here, our multi-dimensional integrated simulation shows that the fast-ignition conditions could be achieved when two 2.8 petawatt heating laser pulses counter-propagate along a 3.5 kilotesla external magnetic field. Within a period of 5 picoseconds, the laser pulses heat a nuclear fuel to reach the ignition conditions. Furthermore, we present the parameter windows of lasers and magnetic fields required for ignition for experimental test. To achieve controlled nuclear fusion energy, the central ignition concept of inertial confinement fusion (ICF) was proposed in 1970s [1-4].
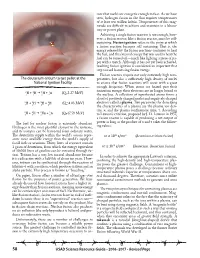
  • USAD Science Resource Guide • 2016–2017 • Revised Page The

    USAD Science Resource Guide • 2016–2017 • Revised Page The

    sure that nuclei are energetic enough to fuse. As we have seen, hydrogen fusion in the Sun requires temperatures of at least ten million kelvin. Temperatures of this mag- nitude are difficult to achieve and maintain in a labora- tory or power plant. Achieving a single fusion reaction is not enough, how- ever; a fusion reactor, like a fission reactor, must be self- sustaining. Fusion ignition refers to the point at which a fusion reaction becomes self-sustaining. That is, the energy released by the fusion reactions continues to heat the fuel, and the external energy that was used to heat the fuel can be turned off—much like lighting a piece of pa- per with a match. Although it has not yet been achieved, reaching fusion ignition is considered an important first step toward harnessing fusion energy. The deuterium-tritium target pellet at the Fusion reactors require not only extremely high tem- peratures, but also a sufficiently high density of nuclei National Ignition Facility. to ensure that fusion reactions will occur with a great enough frequency. When atoms are heated past their 2H + 2H 3H + 1n ionization energy, their electrons are no longer bound to 1 1 2 0 (Q=3.27 MeV) the nucleus. A collection of superheated atoms forms a cloud of positively charged nuclei and negatively charged 2H + 2 H 3 H + 1 H 1 1 1 1 (Q=4.03 MeV) electrons called a plasma. Two parameters for describing the characteristics of a plasma are the plasma ion den- τ 2H + 3H 4He + 1n sity, n, and the plasma confinement time, .
  • Arxiv:2105.10954V1 [Physics.Plasm-Ph] 23 May 2021

    Arxiv:2105.10954V1 [Physics.Plasm-Ph] 23 May 2021

    manuscript No. (will be inserted by the editor) Progress toward Fusion Energy Breakeven and Gain as Measured against the Lawson Criterion Samuel E. Wurzel · Scott C. Hsu the date of receipt and acceptance should be inserted later Abstract The Lawson criterion is a key concept in the products exceeds the sum of the energy required to heat pursuit of fusion energy, relating the fuel density n, (en- the fusion fuel and the energy lost from the fusion fuel ergy) confinement time τ, and fuel temperature T to due to radiation, Lawson concluded that the product the energy gain Q of a fusion plasma. The purpose of of fuel density n and pulse duration τ (Lawson used this paper is to explain and review the Lawson crite- t) must exceed a certain threshold value. When ther- rion and to provide a compilation of achieved parame- mal conduction losses are included (extending Lawson's ters for a broad range of historical and contemporary analysis), the product of n and energy confinement time fusion experiments. Although this paper focuses on the τE must exceed a certain threshold value. We call this Lawson criterion, it is only one of many equally impor- product nτE (also nτ) the Lawson parameter. A suffi- tant factors in assessing the progress and ultimate like- ciently high T is implied such that the energy of charged lihood of any fusion concept becoming a commercially fusion products overcomes radiation losses. These con- viable fusion energy system. Only experimentally mea- ditions are now known as the Lawson criterion. A fusion sured or inferred values of n, τ, and T that have been plasma that has reached these conditions is said to have published in the peer-reviewed literature are included achieved ignition.
  • Road Map to Clean Energy Using Laser Beam Ignition of Boron-Hydrogen Fusion

    Road Map to Clean Energy Using Laser Beam Ignition of Boron-Hydrogen Fusion

    Laser and Particle Beams (2017), 35, 730–740. © Cambridge University Press, 2017 0263-0346/17 doi:10.1017/S0263034617000799 Road map to clean energy using laser beam ignition of boron-hydrogen fusion H. HORA,1 S. ELIEZER,2,4 G.J. KIRCHHOFF,3 N. NISSIM,2,5 J.X. WANG,6 P. LALOUSIS,7 Y.X. XU,6 8 4 9 9 G.H. MILEY, J.M. MARTINEZ-VAL, W. MCKENZIE, AND J. KIRCHHOFF 1Department of Theoretical Physics, University of New South Wales, Sydney 2052, Australia 2SOREQ Research Centre, Yavne, Israel 3UJG Management GmbH, 85586 Poing, Germany 4Polytechnique University, Madrid, Spain 5Department of Earth and Planetary Science, University of California, Berkeley, CA 94720, USA 6State Key Laboratory of Precision Spectroscopy, East China Normal University, Shanghai 200062, China 7Institute of Electronic Structure and Laser FORTH, Heraklion, Greece 8Department Nuclear, Plasma & Radiol. Engineering, University of Illinois, Urbana IL, USA 9HB11 Energy Pty. Ltd., Sydney, Australia (RECEIVED 26 September 2017; ACCEPTED 16 October 2017) Abstract With the aim to overcome the problems of climatic changes and rising ocean levels, one option is to produce large-scale sustainable energy by nuclear fusion of hydrogen and other very light nuclei similar to the energy source of the sun. Sixty years of worldwide research for the ignition of the heavy hydrogen isotopes deuterium (D) and tritium (T) have come close to a breakthrough for ignition. The problem with the DT fusion is that generated neutrons are producing radioactive waste. One exception as the ideal clean fusion process – without neutron production – is the fusion of hydrogen (H) with the boron isotope 11B11 (B11).
  • ICF Ignition, the Lawson Criterion and Comparison with MCF FSC Deuterium–Tritium Plasmas 100 Ignition

    ICF Ignition, the Lawson Criterion and Comparison with MCF FSC Deuterium–Tritium Plasmas 100 Ignition

    ICF Ignition, the Lawson Criterion and Comparison with MCF FSC Deuterium–Tritium Plasmas 100 Ignition E Q ~ 10 x i OMEGA (2009) T i 10 Q ~ 1 n Q = Tokamaks 1993–1999 W /W ) Fusion Input Q ~ 0.1 1 W = energy Laser direct kev s kev Q ~ 0.01 3 drive (1996) – 0.1 m Q ~ 0.001 Laser direct 20 0.01 drive (1986) 10 ( Q ~ 0.0001 Laser indirect 0.001 drive (1986) Q ~ 0.00001 Lawson fusion parameter, Lawson fusion parameter, 0.0001 0.1 1 10 100 “Review of Burning Plasma Physics,” Central ion temperature (keV) FESAC Report (September 2001). 51st Annual Meeting of the R. Betti American Physical Society University of Rochester Division of Plasma Physics Fusion Science Center and Atlanta, GA Laboratory for Laser Energetics 2–6 November 2009 Collaborators FSC K. S. Anderson (UO5.00004) P. Chang (TO5.00004) R. Nora C. D. Zhou University of Rochester Laboratory for Laser Energetics B. Spears (UO5.00013) J. Edwards S. Haan J. Lindl Lawrence Livermore National Laboratory Summary The measurable Lawson criterion and hydro-equivalent curves determine the requirements for an early hydro-equivalent demonstration of ignition on OMEGA and on the NIF (THD) FSC • Cryogenic implosions on OMEGA have achieved a Lawson parameter PxE á 1 atm-s comparable to large tokamaks • Performance requirements for hydroequivalent ignition on OMEGA and NIF (THD)* GtRH GT H YOC Px Hydro-equivalent ignition n i n E g/cm2 keV (atm s) 15% OMEGA (25 kJ) ~0.30 ~3.4 (~3 × 1013 2.6 neutrons) NIF (THD) ~1.8 ~4.7 ~40% 20 * NIF will begin the cryogenic implosion campaign using a surrogate Tritium– Hydrogen–Deuterium (THD) target.
  • Computer Simulations of the ITER Fusion Reactor Federico D

    Computer Simulations of the ITER Fusion Reactor Federico D

    Computer simulations of the ITER fusion reactor Federico D. Halpern*, Glenn Bateman, Christopher M. Wolfe, Alexei Pankin, and A. H. Kritz Department of Physics, Lehigh University ITER [1], the thermonuclear experimental device currently under construction in France, is the first fusion reactor that is expected to produce large amounts of power. In ITER, energy will be produced from the fusion of hydrogen isotopes (deuterium and tritium) into helium. In order to overcome the electrostatic repulsion between atomic nuclei, the mixture of deuterium and tritium gas must be heated to extremely high temperatures. The resulting gas forms a plasma in which atomic nuclei and electrons are no longer bound together. Fusion reactors such as ITER confine plasmas using strong magnetic fields. Plasmas must be confined for a long enough period of time at sufficiently high temperature and density to produce more fusion power than input power. This energy confinement prerequisite for fusion, usually expressed using the Lawson criterion [2], cannot be achieved in present day reactors. ITER is expected to confine plasma discharges for 500 seconds, at a density of 1020 m-3, and a temperature of 20 KeV, which is about 15 times the temperature of the center of the sun. It is anticipated that ITER will produce about ten times more fusion power than input power. The first plasma operation is projected to be in 2017. In the research described here, the performance of ITER is predicted with computer modeling simulations that are carried Figure 1: Rendition of the ITER design. To illustrate out using leading theory-based models for the colossal scale of the device, a person is shown whole-device simulations.
  • Fusion Power a Ten-Year Plan for American Energy Security

    Fusion Power a Ten-Year Plan for American Energy Security

    Fusion Power A Ten-Year Plan for American Energy Security 1 Andrew Holland and Nick Cunningham BOARD OF DIRECTORS The Honorable Gary Hart, Chairman Admiral William Fallon, USN (Ret.) Senator Hart served the State of Colorado in the Admiral Fallon has led U.S. and Allied forces and U.S. Senate and was a member of the Committee played a leadership role in military and diplomatic on Armed Services during his tenure. matters at the highest levels of the U.S. government. Norman R. Augustine Raj Fernando Mr. Augustine was Chairman and Principal Raj Fernando is CEO and founder of RGY Officer of the American Red Cross for nine Chopper Trading, a technology based trading years and Chairman of the Council of the firm headquartered in Chicago. E National Academy of Engineering. The Hon. Donald Beyer Vice Admiral Lee Gunn, USN (Ret.) N The Hon. Donald Beyer is the former United Vice Admiral Gunn is the President of the States Ambassador to to Switzerland and Institute of Public Research at the CNA Liechtenstein, as well as a former Lieutenant Corporation, a non-profit corporation in Virginia. Governor and President of the Senate of Virginia. E The Hon. Jeffery Bleich Lieutenant General Claudia Kennedy, USA (Ret.) The Hon. Jeffery Bleich heads the Global Practice Lieutenant General Kennedy was the first woman for Munger, Tolles & Olson. He served as the U.S. to achieve the rank of three-star general in the Ambassador to Australia from 2009 to 2013. He United States Army. previously served in the Clinton Administration. General Lester L.
  • Extreme Laser Pulses for Non-Thermal Fusion Ignition of Hydrogen–Boron for Clean and Cambridge.Org/Lpb Low-Cost Energy

    Extreme Laser Pulses for Non-Thermal Fusion Ignition of Hydrogen–Boron for Clean and Cambridge.Org/Lpb Low-Cost Energy

    Laser and Particle Beams Extreme laser pulses for non-thermal fusion ignition of hydrogen–boron for clean and cambridge.org/lpb low-cost energy 1,2 3,4 5 6 6 Review Article Heinrich Hora , Shalom Eliezer , George H. Miley , JiaXiang Wang , YanXia Xu and Noaz Nissim3 Cite this article: Hora H, Eliezer S, Miley GH, Wang J, Xu Y, Nissim N (2018). Extreme laser 1University of New South Wales, Sydney 2052, Australia; 2HB11 Energy Pty. Ltd., Sydney, Australia; 3Soreq NRC, pulses for non-thermal fusion ignition of 4 5 – Yavne, Israel; Polytechnique University, Madrid, Spain; Department of Nuclear Plasma and Radiological hydrogen boron for clean and low-cost 6 energy. Laser and Particle Beams 36,335–340. Engineering, University of Illinois, Urbana IL, USA and State Key Laboratory of Precision Spectroscopy, https://doi.org/10.1017/S0263034618000289 Science Building A908a, East China Normal University, Shanghai 200062, China Received: 7 June 2018 Abstract Accepted: 17 July 2018 After achieving significant research results on laser-driven boron fusion, the essential facts are Key words: presented how the classical very low-energy gains of the initially known thermal ignition con- Clean energy; extreme power laser pulses; ditions for fusion of hydrogen (H) with the boron isotope 11 (HB11 fusion) were bridged by hydrogen–boron fusion; non-thermal fusion; plasma blocks nine orders of magnitudes in agreement with experiments. This is possible under extreme non-thermal equilibrium conditions for ignition by >10 PW-ps laser pulses of extreme Author for correspondence: power and nonlinear conditions. This low-temperature clean and low-cost fusion energy Heinrich Hora, University of New South Wales, generation is in crucial contrast to local thermal equilibrium conditions with the advantage Sydney 2052, Australia.