Voting with Partially-Ordered Preferences
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-
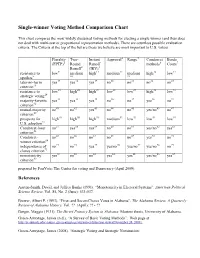
Single-Winner Voting Method Comparison Chart
Single-winner Voting Method Comparison Chart This chart compares the most widely discussed voting methods for electing a single winner (and thus does not deal with multi-seat or proportional representation methods). There are countless possible evaluation criteria. The Criteria at the top of the list are those we believe are most important to U.S. voters. Plurality Two- Instant Approval4 Range5 Condorcet Borda (FPTP)1 Round Runoff methods6 Count7 Runoff2 (IRV)3 resistance to low9 medium high11 medium12 medium high14 low15 spoilers8 10 13 later-no-harm yes17 yes18 yes19 no20 no21 no22 no23 criterion16 resistance to low25 high26 high27 low28 low29 high30 low31 strategic voting24 majority-favorite yes33 yes34 yes35 no36 no37 yes38 no39 criterion32 mutual-majority no41 no42 yes43 no44 no45 yes/no 46 no47 criterion40 prospects for high49 high50 high51 medium52 low53 low54 low55 U.S. adoption48 Condorcet-loser no57 yes58 yes59 no60 no61 yes/no 62 yes63 criterion56 Condorcet- no65 no66 no67 no68 no69 yes70 no71 winner criterion64 independence of no73 no74 yes75 yes/no 76 yes/no 77 yes/no 78 no79 clones criterion72 81 82 83 84 85 86 87 monotonicity yes no no yes yes yes/no yes criterion80 prepared by FairVote: The Center for voting and Democracy (April 2009). References Austen-Smith, David, and Jeffrey Banks (1991). “Monotonicity in Electoral Systems”. American Political Science Review, Vol. 85, No. 2 (June): 531-537. Brewer, Albert P. (1993). “First- and Secon-Choice Votes in Alabama”. The Alabama Review, A Quarterly Review of Alabama History, Vol. ?? (April): ?? - ?? Burgin, Maggie (1931). The Direct Primary System in Alabama. -

Ranked-Choice Voting from a Partisan Perspective
Ranked-Choice Voting From a Partisan Perspective Jack Santucci December 21, 2020 Revised December 22, 2020 Abstract Ranked-choice voting (RCV) has come to mean a range of electoral systems. Broadly, they can facilitate (a) majority winners in single-seat districts, (b) majority rule with minority representation in multi-seat districts, or (c) majority sweeps in multi-seat districts. Such systems can be combined with other rules that encourage/discourage slate voting. This paper describes five major versions used in U.S. public elections: Al- ternative Vote (AV), single transferable vote (STV), block-preferential voting (BPV), the bottoms-up system, and AV with numbered posts. It then considers each from the perspective of a `political operative.' Simple models of voting (one with two parties, another with three) draw attention to real-world strategic issues: effects on minority representation, importance of party cues, and reasons for the political operative to care about how voters rank choices. Unsurprisingly, different rules produce different outcomes with the same votes. Specific problems from the operative's perspective are: majority reversal, serving two masters, and undisciplined third-party voters (e.g., `pure' independents). Some of these stem from well-known phenomena, e.g., ballot exhaus- tion/ranking truncation and inter-coalition \vote leakage." The paper also alludes to vote-management tactics, i.e., rationing nominations and ensuring even distributions of first-choice votes. Illustrative examples come from American history and comparative politics. (209 words.) Keywords: Alternative Vote, ballot exhaustion, block-preferential voting, bottoms- up system, exhaustive-preferential system, instant runoff voting, ranked-choice voting, sequential ranked-choice voting, single transferable vote, strategic coordination (10 keywords). -

Democracy Without Elections Mainz
Democracy without Elections: Is electoral accountability essential for democracy? Felix Gerlsbeck [email protected] Paper prepared for the workshop “Democratic Anxiety. Democratic Resilience.” Mainz, 15-17 June 2017 DRAFT VERSION, PLEASE DO NOT CITE WITHOUT AUTHOR’S PERMISSION 1. Introduction The idea of choosing political decision-makers by sortition, that is, choosing them randomly from a pool of the entire population or from some qualified subset, through some form of lottery or other randomizing procedure, is familiar to democrats at least since ancient Athens. Apart from the selection of trial juries, however, sortition has all but disappeared from official decision-making procedures within contemporary democratic systems, and free, equal, and regular election through voting by the entire qualified population of candidates who put themselves forward for political office, has taken its place. Nevertheless, there has been renewed interest in the idea of reviving sortition-based elements within modern democratic systems over the last years: a number of democratic theorists see great promise in complementing elected decision-making institutions with those selected randomly. These proposals variously go under the names mini-publics, citizen juries, citizen assemblies, lottocracy, enfranchisement lottery, and even Machiavellian Democracy.1 The roots of this practice go back to ancient Athens. During the 5th century Athenian democracy, the equivalent of the parliamentary body tasked with deliberating 1 See for instance, Guerrero 2014; Fishkin 2009; Warren & Gastil 2015; Ryan & Smith 2014; Saunders 2012; López-Guerra 2014; López-Guerra 2011; McCormick 2011. 1 and drafting policy proposals, the boule, was chosen by lot from the citizens of Athens through a complex system of randomization. -

2016 US Presidential Election Herrade Igersheim, François Durand, Aaron Hamlin, Jean-François Laslier
Comparing Voting Methods: 2016 US Presidential Election Herrade Igersheim, François Durand, Aaron Hamlin, Jean-François Laslier To cite this version: Herrade Igersheim, François Durand, Aaron Hamlin, Jean-François Laslier. Comparing Voting Meth- ods: 2016 US Presidential Election. 2018. halshs-01972097 HAL Id: halshs-01972097 https://halshs.archives-ouvertes.fr/halshs-01972097 Preprint submitted on 7 Jan 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. WORKING PAPER N° 2018 – 55 Comparing Voting Methods: 2016 US Presidential Election Herrade Igersheim François Durand Aaron Hamlin Jean-François Laslier JEL Codes: D72, C93 Keywords : Approval voting, range voting, instant runoff, strategic voting, US Presidential election PARIS-JOURDAN SCIENCES ECONOMIQUES 48, BD JOURDAN – E.N.S. – 75014 PARIS TÉL. : 33(0) 1 80 52 16 00= www.pse.ens.fr CENTRE NATIONAL DE LA RECHERCHE SCIENTIFIQUE – ECOLE DES HAUTES ETUDES EN SCIENCES SOCIALES ÉCOLE DES PONTS PARISTECH – ECOLE NORMALE SUPÉRIEURE INSTITUT NATIONAL DE LA RECHERCHE AGRONOMIQUE – UNIVERSITE PARIS 1 Comparing Voting Methods: 2016 US Presidential Election Herrade Igersheim☦ François Durand* Aaron Hamlin✝ Jean-François Laslier§ November, 20, 2018 Abstract. Before the 2016 US presidential elections, more than 2,000 participants participated to a survey in which they were asked their opinions about the candidates, and were also asked to vote according to different alternative voting rules, in addition to plurality: approval voting, range voting, and instant runoff voting. -

City Council Election Methods in Order to Ensure That the Election Please Do Not Hesitate to Contact Us
The Center for Voting and Democracy City 6930 Carroll Avenue, Suite 610 – Takoma Park, MD 20912 Phone: (301) 270-4616 – Fax: (301) 270-4133 Council Email: [email protected] Website: http://www.fairvote.org Election This Manual is intended to assist Charter Review Comissions, city officials, and other community Methods leaders in determining what electoral systems will best meet the needs and goals of their community. Given that no system can accomplish every goal, this manual will help you analyze the INTRODUCTION consequences of adopting one system over The range of options that exists for electing a municipal government is broader than many people realize. Voting systems can have a another and will aid you in comparing the features striking impact on the type of candidates who run for office, how of various electoral systems. representative the council is, which candidates are elected, which parties control the city council, which voters feel well represented, Should you desire more information about any of and so on. This booklet is intended to aid in the evaluation of possible the voting systems discussed within this manual, city council election methods in order to ensure that the election please do not hesitate to contact us. method is determined by conscious choice, not inertia. A separate companion booklet, Mayoral Election Methods , deals with the selection of an executive. A summary of this booklet can be found in the city council election method evaluation grid at Page 11. 1 CRITERIA FOR EVALUATING CITY COUNCIL ELECTION METHODS 1. VOTER CHOICE Different election methods will encourage different numbers of It is important to recognize from the outset that no election candidates to run, and will thus impact the level of choice which method is perfect. -

Democracy in the Age of Pandemic – Fair Vote UK Report June 2020
Democracy in the Age of Pandemic How to Safeguard Elections & Ensure Government Continuity APPENDICES fairvote.uk Published June 2020 Appendix 1 - 86 1 Written Evidence, Responses to Online Questionnaire During the preparation of this report, Fair Vote UK conducted a call for written evidence through an online questionnaire. The questionnaire was open to all members of the public. This document contains the unedited responses from that survey. The names and organisations for each entry have been included in the interest of transparency. The text of the questionnaire is found below. It indicates which question each response corresponds to. Name Organisation (if applicable) Question 1: What weaknesses in democratic processes has Covid-19 highlighted? Question 2: Are you aware of any good articles/publications/studies on this subject? Or of any countries/regions that have put in place mediating practices that insulate it from the social distancing effects of Covid-19? Question 3: Do you have any ideas on how to address democratic shortcomings exposed by the impact of Covid-19? Appendix 1 - 86 2 Appendix 1 Name S. Holledge Organisation Question 1 Techno-phobia? Question 2 Estonia's e-society Question 3 Use technology and don't be frightened by it 2 Appendix 1 - 86 3 Appendix 2 Name S. Page Organisation Yes for EU (Scotland) Question 1 The Westminster Parliament is not fit for purpose Question 2 Scottish Parliament Question 3 Use the internet and electronic voting 3 Appendix 1 - 86 4 Appendix 3 Name J. Sanders Organisation emergency legislation without scrutiny removing civil liberties railroading powers through for example changes to mental health act that impact on individual rights (A) Question 1 I live in Wales, and commend Mark Drakeford for his quick response to the crisis by enabling the Assembly to continue to meet and debate online Question 2 no, not until you asked. -

Download Legal Document
Case: 4:14-cv-02077-RWS Doc. #: 212 Filed: 11/21/16 Page: 1 of 26 PageID #: 9139 UNITED STATES DISTRICT COURT EASTERN DISTRICT OF MISSOURI EASTERN DIVISION MISSOURI STATE CONFERENCE ) OF THE NATIONAL ASSOCIATION ) FOR THE ADVANCEMENT OF ) COLORED PEOPLE, et al., ) ) Plaintiffs, ) ) vs. ) Case No. 4:14 CV 2077 RWS ) FERGUSON-FLORISSANT ) SCHOOL DISTRICT, et al., ) ) Defendants. ) REMEDIAL ORDER Plaintiffs Doris Bailey, Redditt Hudson, F. Willis Johnson, and the Missouri State Conference of the National Association for the Advancement of Colored People filed suit against Defendants Ferguson-Florissant School District (the School District) and the St. Louis County Board of Election Commissioners (the Election Board) under Section 2 of the Voting Rights Act of 1965, 52 U.S.C. § 10301. Plaintiffs alleged that the electoral structures used in Ferguson-Florissant School Board elections, together with historical and socioeconomic conditions, deprive African American voters in the School District of an equal opportunity to elect representatives of their choice. After a six-day non-jury trial and post-trial briefing, I concluded Plaintiffs established a Section 2 violation. I enjoined Defendants from conducting any elections for the Ferguson-Florissant School Case: 4:14-cv-02077-RWS Doc. #: 212 Filed: 11/21/16 Page: 2 of 26 PageID #: 9140 Board until a new system is properly implemented. See Mem. Op. & Order, ECF No. 185. At a status conference held to discuss remedies, Defendants were afforded the first opportunity to submit a remedial plan, but the School District stated it preferred that Plaintiffs, rather than the School District, submit initial remedial proposals for the Court’s consideration. -

Approval Voting
Approval Voting 21-301 2018 3 May 1 Approval Voting All of the voting methods we have yet discussed are what is known as \preferential voting" methods. In a preferential voting system, voters are asked for their specific preferences regarding candidates: who do you prefer most, who in second place, etc. Nonpreferential voting is a variant in which voters do not rank candidates, but instead divide into categories of \acceptable" and \unacceptable." The following schema include some elements of nonpreferential voting, although some combine preferential and nonpreferential ideas. 1.1 Approval Voting: Basics In an approval voting system, each voter indicates, for each candidate, whether they approve of that choice or not. There is no ranking necessary. The candidate that then has the highest number of approvals goes on to win the election. Approval voting has gotten some recent support in political circles as a way of preventing a so-called \spoiler" candidate from taking support away from an otherwise viable first-choice candidate. If voters are permitted to approve multiple candidates, then they can vote both for the major candidate and the minor \spoiler." In addition, proponents of approval voting say that such systems reduce negative campaigning, as your goal is not to become a \lesser of two evils" but to maximize the number of voters who approve of you (this claim is hotly debated, but we've veered now into the crossover between mathematics and behavioral science). Criticisms of this approach center around the tendency of voters to engage in \bullet" voting, that is, voting only for their first choice preferred candidate rather than all those they approve; and the tendency of voters to approve of a candidate that they may not actually approve in order to prevent a different candidate from winning. -

Voting Systems: from Method to Algorithm
Voting Systems: From Method to Algorithm A Thesis Presented to The Faculty of the Com puter Science Department California State University Channel Islands In (Partial) Fulfillment of the Requirements for the Degree M asters of Science in Com puter Science b y Christopher R . Devlin Advisor: Michael Soltys December 2019 © 2019 Christopher R. Devlin ALL RIGHTS RESERVED APPROVED FOR MS IN COMPUTER SCIENCE Advisor: Dr. Michael Soltys Date Name: Dr. Bahareh Abbasi Date Name: Dr. Vida Vakilian Date APPROVED FOR THE UNIVERITY Name Date Acknowledgements I’d like to thank my wife, Eden Byrne for her patience and support while I completed this Masters Degree. I’d also like to thank Dr. Michael Soltys for his guidance and mentorship. Additionally I’d like to thank the faculty and my fellow students at CSUCI who have given nothing but assistance and encouragement during my time here. Voting Systems: From Method to Algorithm Christopher R. Devlin December 18, 2019 Abstract Voting and choice aggregation are used widely not just in poli tics but in business decision making processes and other areas such as competitive bidding procurement. Stakeholders and others who rely on these systems require them to be fast, efficient, and, most impor tantly, fair. The focus of this thesis is to illustrate the complexities inherent in voting systems. The algorithms intrinsic in several voting systems are made explicit as a way to simplify choices among these systems. The systematic evaluation of the algorithms associated with choice aggregation will provide a groundwork for future research and the implementation of these tools across public and private spheres. -

APPENDIX T* * * * ** * * * * * ** * * * * * * * * * **************************** * "·"""1
*************************** * * * * * * * * * * * ** * * * * t* APPENDIX t* * * * ** * * * * * ** * * * * * * * * * **************************** * "·"""1 ~ : , ' • ~.;~\ flbntgomery Cbunty Cbvemmenl ROCKVILLE, MARYLAND 20850 February 28,2014 Montgomery County Council Stella Werner Council Office Building 100 Maryland A venue, 6th Floor Rockvil Ie, Maryland 20850 Dear Councilmembers: Thank you on behalf ofthe entire Right to Vote Task Force for the creation of this effort to evaluate election laws and practices and for our appointment to the Task Force. Since being appointed on November 26,2013 the full Task Force has met for more than 6 hours to initially discuss the Actions assigned, assess topics associated with the Actions, and divide the workload across all members. This document is the interim report requested for delivery on February 28, 2014 on our progress to date and the Task Force is on track to complete a final report due by May 31, 2014. We have organized ourselves into three subcommittees to focus on the tasks assigned, with each subcommittee having from four to five members. These subcommittees meet on a weekly or biweekly basis until the final report is ready for delivery. The subcommittees are: Registration: This subcommittee is recommending changes that would increase voter participation, developing plans to promote same-day registration and recommendations to Council to strengthen such efforts, evaluate and make recommendations on high school voter registration efforts. The subcommittee is also evaluating whether the General Assembly should allow automatic voter registration or other 'opt-in' approaches to registration. Access: This subcommittee is evaluating voter education programs and plans to promote early voting. Voting Rights: This subcommittee is reviewing local laws and practices that may affect the right to vote and will be recommending changes that would strengthen the right to vote in the county. -

Kids Voting Usa 9-12 Classroom Activities
KIDS VOTING USA 9-12 CLASSROOM ACTIVITIES TABLE OF CONTENTS EDUCATOR’S GUIDE OVERVIEW SCOPE AND SEQUENCE INDEX TO ACTIVITIES BY SKILL AND DISCIPLINE CLASSROOM ACTIVITIES ELECTIONS AND THE VOTING EXPERIENCE AMERICAN DEMOCRACY AND CITIZENSHIP SUFFRAGE AND THE RIGHT TO VOTE ACTIVE CITIZENSHIP ADDITIONAL RESOURCES APPENDIX GLOSSARY BIBLIOGRAPHY LOCAL INFORMATION KIDS VOTING USA 9–12 EDUCATOR’S GUIDE Copyright © 2005 Kids Voting USA, Inc. All rights reserved. The materials contained herein are protected by copyright laws, and may not be reproduced, republished, distributed, transmitted or otherwise exploited in any manner without the express prior written permission of Kids Voting USA. The Kids Voting USA name and logo and all related trademarks, trade names, and other intellectual property are the property of Kids Voting USA and cannot be used without its express prior written permission. 9–12 EDUCATOR’S GUIDE TABLE OF CONTENTS AN OVERVIEW . 2 SCOPE AND SEQUENCE . 6 INDEX TO ACTIVITIES BY SKILL . 8 INDEX TO ACTIVITIES BY DISCIPLINE . 10 INDEX TO ACTIVITIES BY ADDITIONAL CATEGORIES . 11 THE TEACHER AND THE TOWN . 12 EDUCATOR’S GUIDE 1 ©2005 Kids Voting USA, Inc. – All rights reserved. 9–12 EDUCATOR’S GUIDE AN OVERVIEW WHAT IS KIDS VOTING USA? Kids Voting USA (KVUSA) is a national nonprofit organization working to secure the future of democracy by preparing young people to be educated, engaged voters. KVUSA operates through a national network of community-based affiliates that partner with schools and election officials. The program offers students in kindergarten through high school a wide range of opportunities for civic learning. It is the combination of classroom instruction, family dialogue, and an authentic voting experience throughout a young person’s formative years that makes Kids Voting USA a powerful strategy for achieving long-term change in voting behavior. -

Why Approval Voting Is Unworkable in Contested Elections
Why Approval Voting is Unworkable in Contested Elections And How the Borda Count, Score Voting, Range Voting and Bucklin Voting are Similarly Flawed Due to Vulnerability to Strategic Voting An Analysis by FairVote, July 2011 Summary Approval voting is a method of voting to elect single winners that has adherents among some voting theorists, but is unworkable in contested elections in which voters have a stake in the outcome. Once aware of how approval voting works, strategic voters will always earn a significant advantage over less informed voters. This problem with strategic voting far outweighs any other factor when evaluating the potential use of approval voting in governmental elections. Among other methods that should not be used in meaningfully contested elections are range voting, score voting, the Borda Count and Bucklin voting. They all share approval voting’s practical flaw of not allowing voters to support a second choice without potentially causing the defeat of their first choice. Such voting methods have their potential value, but only in elections where voters have no particular stake in the outcome. The only voting methods that should be weighed seriously for governmental elections are methods that do not violate this “later-no-harm” criterion (plurality voting and forms of runoff elections and instant runoff voting [http://www.instantrunoff.com] ) or only do so indirectly (such as Condorcet voting methods). We support our claims about approval voting and similar voting methods both with theoretical analysis and with a broad range of evidence, including the failure of these voting methods in every single significant use in meaningfully contested elections.