Picometre-Precision Analysis of Scanning Transmission Electron Microscopy Images of Platinum Nanocatalysts
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Measurement-Resource-Book-1.Pdf
First Steps in Mathematics Measurement Understand Units and Resource Book 1 Direct Measure Improving the mathematics outcomes of students FSIM010 | First Steps in Mathematics: Measurement Book 1 © Western Australian Minister for Education 2013. Published by Pearson Canada Inc. First Steps in Mathematics: Measurement Resource Book 1 Understand Units and Direct Measure © Western Australian Minister for Education 2013 Published in Canada by Pearson Canada Inc. 26 Prince Andrew Place Don Mills, ON M3C 2T8 Text by Sue Willis with Wendy Devlin, Lorraine Jacob, Beth Powell, Dianne Tomazos, and Kaye Treacy for STEPS Professional Development on behalf of the Department of Education and Training, Western Australia. Photos: Ray Boudreau Illustrations: Neil Curtis, Vesna Krstanovich and David Cheung ISBN-13: 978-0-13-188205-8 ISBN-10: 0-13-188205-8 Publisher: Debbie Davidson Director, Pearson Professional Learning: Terry (Theresa) Nikkel Research and Communications Manager: Chris Allen Canadian Edition Consultants: Craig Featherstone, David McKillop, Barry Onslow Development House: Pronk&Associates Project Coordinator: Joanne Close Art Direction: Jennifer Stimson and Zena Denchik Design: Jennifer Stimson and David Cheung Page Layout: Computer Composition of Canada Inc. FSIM010 | First Steps in Mathematics: Measurement Book 1 © Western Australian Minister for Education 2013. Published by Pearson Canada Inc. Diagnostic Map: Measurement Matching and Emergent Phase Comparing Phase Quantifying Phase Most students will enter the Matching and Most students -

Orders of Magnitude (Length) - Wikipedia
03/08/2018 Orders of magnitude (length) - Wikipedia Orders of magnitude (length) The following are examples of orders of magnitude for different lengths. Contents Overview Detailed list Subatomic Atomic to cellular Cellular to human scale Human to astronomical scale Astronomical less than 10 yoctometres 10 yoctometres 100 yoctometres 1 zeptometre 10 zeptometres 100 zeptometres 1 attometre 10 attometres 100 attometres 1 femtometre 10 femtometres 100 femtometres 1 picometre 10 picometres 100 picometres 1 nanometre 10 nanometres 100 nanometres 1 micrometre 10 micrometres 100 micrometres 1 millimetre 1 centimetre 1 decimetre Conversions Wavelengths Human-defined scales and structures Nature Astronomical 1 metre Conversions https://en.wikipedia.org/wiki/Orders_of_magnitude_(length) 1/44 03/08/2018 Orders of magnitude (length) - Wikipedia Human-defined scales and structures Sports Nature Astronomical 1 decametre Conversions Human-defined scales and structures Sports Nature Astronomical 1 hectometre Conversions Human-defined scales and structures Sports Nature Astronomical 1 kilometre Conversions Human-defined scales and structures Geographical Astronomical 10 kilometres Conversions Sports Human-defined scales and structures Geographical Astronomical 100 kilometres Conversions Human-defined scales and structures Geographical Astronomical 1 megametre Conversions Human-defined scales and structures Sports Geographical Astronomical 10 megametres Conversions Human-defined scales and structures Geographical Astronomical 100 megametres 1 gigametre -

6411 Measure Unit Qualifier Indication of the Unit of Measurement in Which Weight (Mass), Capacity, Length, Area, Volume Or Other Quantity Is Expressed
Code list 6411 Standard: UN D.96B S3 6411 Measure unit qualifier Indication of the unit of measurement in which weight (mass), capacity, length, area, volume or other quantity is expressed. Note: See UN/ECE Recommendation 20. 04 small spray 05 lift 08 heat lot 10 group 11 outfit 13 ration 14 shot 15 stick 16 hundred fifteen kg drum 17 hundred lb drum 18 fiftyfive gallon (US) drum 19 tank truck 20 twenty foot container 21 forty foot container 22 decilitre per gram 23 gram per cubic centimetre 24 theoretical pound 25 gram per square centimetre 26 actual ton 27 theoretical ton 28 kilogram per square metre 29 pound per thousand square feet 30 horse power day per air dry metric ton 31 catch weight 32 kilogram per air dry metric ton 33 kilopascal square metres per gram 34 kilopascals per millimetre 35 millilitres per square centimetre second 36 cubic feet per minute per square foot 37 ounce per square foot 38 ounces per square foot per 0,01 inch 40 millilitre per second 41 millilitre per minute 43 super bulk bag 44 fivehundred kg bulk bag 45 threehundred kg bulk bag 46 fifty lb bulk bag 47 fifty lb bag 48 bulk car load 53 theoretical kilograms Printed by GEFEG EDIFIX® Print date: 26/09/2001 Page: 1 Code list 6411 Standard: UN D.96B S3 54 theoretical tonne 56 sitas 57 mesh 58 net kilogram 59 part per million 60 percent weight 61 part per billion (US) 62 percent per 1000 hour 63 failure rate in time 64 pound per square inch, gauge 66 oersted 69 test specific scale 71 volt ampere per pound 72 watt per pound 73 ampere tum per centimetre 74 millipascal -
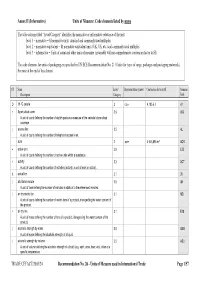
Units of Measure Used in International Trade Page 1/57 Annex II (Informative) Units of Measure: Code Elements Listed by Name
Annex II (Informative) Units of Measure: Code elements listed by name The table column titled “Level/Category” identifies the normative or informative relevance of the unit: level 1 – normative = SI normative units, standard and commonly used multiples level 2 – normative equivalent = SI normative equivalent units (UK, US, etc.) and commonly used multiples level 3 – informative = Units of count and other units of measure (invariably with no comprehensive conversion factor to SI) The code elements for units of packaging are specified in UN/ECE Recommendation No. 21 (Codes for types of cargo, packages and packaging materials). See note at the end of this Annex). ST Name Level/ Representation symbol Conversion factor to SI Common Description Category Code D 15 °C calorie 2 cal₁₅ 4,185 5 J A1 + 8-part cloud cover 3.9 A59 A unit of count defining the number of eighth-parts as a measure of the celestial dome cloud coverage. | access line 3.5 AL A unit of count defining the number of telephone access lines. acre 2 acre 4 046,856 m² ACR + active unit 3.9 E25 A unit of count defining the number of active units within a substance. + activity 3.2 ACT A unit of count defining the number of activities (activity: a unit of work or action). X actual ton 3.1 26 | additional minute 3.5 AH A unit of time defining the number of minutes in addition to the referenced minutes. | air dry metric ton 3.1 MD A unit of count defining the number of metric tons of a product, disregarding the water content of the product. -

Not Made to Measure
Made in Britain: Not made to measure. Ronnie Cohen © 2011 Ronnie Cohen. All rights reserved. 1 Table of Contents Foreword...............................................................................................................................................5 Introduction..........................................................................................................................................6 Central Role of Measurement in Daily Life.........................................................................................7 Why Measurement Matters..................................................................................................................8 Quest for Honest Measurements since Ancient Times.........................................................................9 Measurement Facts: Did you know that....?.......................................................................................10 Description of the British Imperial System........................................................................................11 Introduction to the British Imperial System..............................................................................11 Units of Length..........................................................................................................................11 Units of Area.............................................................................................................................11 Units of Volume........................................................................................................................12 -

Siunitx – a Comprehensive (Si) Units Package∗
siunitx – A comprehensive (si) units package∗ Joseph Wright† Released 2021-09-22 Contents 1 Introduction 3 2 siunitx for the impatient 3 3 Using the siunitx package 4 3.1 Numbers . 4 3.2 Angles . 5 3.3 Units . 6 3.4 Complex numbers and quantities . 7 3.5 The unit macros . 8 3.6 Unit abbreviations . 10 3.7 Creating new macros . 14 3.8 Tabular material . 15 4 Package control options 17 4.1 The key–value control system . 17 4.2 Printing . 18 4.3 Parsing numbers . 20 4.4 Post-processing numbers . 22 4.5 Printing numbers . 25 4.6 Lists, products and ranges . 28 4.7 Complex numbers . 31 4.8 Angles . 32 4.9 Creating units . 34 4.10 Using units . 35 4.11 Quantities . 38 4.12 Tabular material . 39 4.13 Locale options . 49 4.14 Preamble-only options . 49 5 Upgrading from version 2 49 6 Unit changes made by BIPM 51 ∗This file describes v3.0.31, last revised 2021-09-22. †E-mail: [email protected] 1 7 Localisation 52 8 Compatibility with other packages 52 9 Hints for using siunitx 52 9.1 Adjusting \litre and \liter ........................ 52 9.2 Ensuring text or math output . 53 9.3 Expanding content in tables . 53 9.4 Using siunitx with datatool .......................... 54 9.5 Using units in section headings and bookmarks . 55 9.6 A left-aligned column visually centred under a heading . 56 9.7 Regression tables . 57 9.8 Maximising performance . 58 9.9 Special considerations for the \kWh unit . -

Poster Abstracts
1794-A-1902 Influence of the support on stabilizing local defects in strained monolayer oxide films Shuqiu Wang1, Xiao Hu1, Jacek Goniakowski2, Claudine Noguera2, Martin R. Castell1 1 Department of Materials, University of Oxford, Oxford, U.K. 2 CNRS-Sorbonne Université, Paris, France Two-dimensional materials with a honeycomb lattice, such as graphene and hexagonal boron nitride, often contain local defects in which the hexagonal elements are replaced by four, five, seven, and eight-membered rings. An example is the Stone-Wales (S-W) defect, where a bond rotation causes four hexagons to be transformed into a cluster of two pentagons and two heptagons. A further series of similar defects incorporating divacancies results in larger structures of non-hexagonal elements. In this paper, we use scanning tunneling microscopy (STM) and density functional theory (DFT) modeling to investigate the structure and energetics of S-W and divacancy defects in a honeycomb (2 × 2) Ti2O3 monolayer grown on an Au(111) substrate. The epitaxial rumpled Ti2O3 monolayer is pseudomorphic and in a state of elastic compression. As a consequence, divacancy defects, which induce tension in freestanding films, relieve the compression in the epitaxial Ti2O3 monolayer and therefore have significantly lower energies when compared with their freestanding counterparts. We find that at the divacancy defect sites, there is a local reduction of the charge transfer between the film and the substrate, the rumpling is reduced, and the film has an increased separation from the substrate. Our results demonstrate the capacity of the substrate to significantly influence the energetics, and hence favor vacancy-type defects, in compressively strained 2D materials. -

Notes for Authors Notes for Authors SSGCID Special Issue of Acta Cryst. F
notes for authors Acta Crystallographica Section F Structural Biology Notes for Authors and Crystallization SSGCID special issue of Acta Cryst. F Communications ISSN 1744-3091 1. Submission aged but if a reference is unavoidable it should be indicated in the form Smith et al. Authors should read the online submission should be sufficiently full within the Abstract (1998) or (Smith et al., 1998) etc. All authors instructions at http://journals.iucr.org/f/services/ for unambiguous identification, e.g. [Jones should be included in a full list at the end of new_submitinstructions.html and submit (2001). Acta Cryst. D57, 1–10]. the paper. This list should be arranged their paper via the web at http://journals. Authors should supply a synopsis of no alphabetically and conform with the iucr.org/f/services/conferenceproceedings.html. more than two sentences for inclusion in the following style: Papers are expected to be submitted no later contents listing of the journal. Andrews, M. D., Wright, H. E. & Clarke, S. A. than 1 November 2010. (2007). In preparation. 2.5. Units Bru¨nger, A. T. (1992). X-PLOR. Version 3.1. A System for X-ray Crystallography and NMR. 2. Manuscript preparation The International System of Units (SI) is Yale University, Connecticut, USA. ˚ ˚ 2.1. File format used except that the angstro¨m (symbol A, Collaborative Computational Project, Number 4 defined as 10À10 m) is generally preferred to The source files required for a paper are: a (1994). Acta Cryst. D50, 760–763. the nanometre (nm) or picometre (pm) as single file in Word, RTF or LAT X format of Crowther, R. -

Laser Actuation of Cantilevers for Picometre Amplitude Dynamic
OPEN Laser Actuation of Cantilevers for SUBJECT AREAS: Picometre Amplitude Dynamic Force CHARACTERIZATION AND ANALYTICAL Microscopy TECHNIQUES POLYMERS Drew R. Evans1,2, Ponlawat Tayati1, Hongjie An1, Ping Koy Lam3, Vincent S. J. Craig1 & Tim J. Senden1 CHEMICAL PHYSICS 1Department of Applied Mathematics, Research School of Physics and Engineering, The Australian National University, Canberra, ACT, 0200, Australia, 2Thin Film Coatings Group, Mawson Institute, University of South Australia, Mawson Lakes, SA 5095, Received 3 Australia, Department of Quantum Science, Research School of Physics and Engineering, The Australian National University, 24 March 2014 Canberra, ACT, 0200, Australia. Accepted 5 June 2014 As nanoscale and molecular devices become reality, the ability to probe materials on these scales is Published increasing in importance. To address this, we have developed a dynamic force microscopy technique where 4 July 2014 the flexure of the microcantilever is excited using an intensity modulated laser beam to achieve modulation on the picoscale. The flexure arises from thermally induced bending through differential expansion and the conservation of momentum when the photons are reflected and absorbed by the cantilever. In this study, we investigated the photothermal and photon pressure responses of monolithic and layered cantilevers using a Correspondence and modulated laser in air and immersed in water. The developed photon actuation technique is applied to the requests for materials stretching of single polymer chains. should be addressed to T.J.S. (tim.senden@ he Atomic Force Microscope (AFM) is widely used for high resolution imaging of surfaces, performing force anu.edu.au) or analysis, surface characterization1,2, and manipulating molecular systems ranging from DNA3 and motor V.S.J.C. -

The International System of Units (SI)
—————————————————————————— Bureau International des Poids et Mesures The International System of Units (SI) 9th edition 2019 ———————————————— v1.08 Copyright statement The SI Brochure is distributed under the terms of the Creative Commons Attribution 3.0 IGO (https://creativecommons.org/licenses/by/3.0/igo/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The BIPM and the Metre Convention • 117 The BIPM and the Metre Convention The International Bureau of Weights and Measures (BIPM) was set up by the Metre As of 20 May 2019 there Convention signed in Paris on 20 May 1875 by seventeen States during the final session of were fifty nine Member States: Argentina, Australia, the diplomatic Conference of the Metre. This Convention was amended in 1921. Austria, Belgium, Brazil, Bulgaria, Canada, Chile, 2 The BIPM has its headquarters near Paris, in the grounds (43 520 m ) of the Pavillon de China, Colombia, Croatia, Breteuil (Parc de Saint-Cloud) placed at its disposal by the French Government; its upkeep Czech Republic, Denmark, Egypt, Finland, France, is financed jointly by the Member States of the Metre Convention. Germany, Greece, Hungary, India, Indonesia, Iran (Islamic The task of the BIPM is to ensure worldwide unification of measurements; its objectives are Rep. of), Iraq, Ireland, Israel, to: Italy, Japan, Kazakhstan, Kenya, Korea (Republic of), -

10.01A Units and Measurement
Topic Check In - 10.01a Units and measurement 1. Complete this statement. 2000 mm = ___________ m 2. State the volume of a 10 cm by 10 cm by 10 cm cube and the capacity of a box of the same dimensions. Volume ___________ cm3 Capacity ___________ litres 600 cm 3. The diagram opposite shows a garden lawn. 100 cm State appropriate units for the area of the lawn. 500 cm 200 cm 400 cm 4. A coach takes 3 hours 50 minutes to complete a journey from Manchester to London. If the coach leaves Manchester at 09:25, what time does it arrive in London? 5. The luggage allowance on a British flight is 23 kg. If your luggage weighs 21 kg 35 g, how much more weight could you take? 1 6. Show that 142 minutes is less than 2 hours. 2 2 2 7. Show that 700 cm is the same as 0.07 m . 8. Given that 1 inch is approximately 2.5 cm, show that a 12 inch ruler is approximately 30 cm. 9. Farook is designing a photo montage poster for the PE department. What is the maximum number of 5 cm by 4 cm photographs that he can fit (without overlap) on his 2 m by 2 m piece of card? 10. Here is a recipe for pancakes. Recipe for 10 pancakes Simon looks up the prices of the ingredients on the internet. 100 g flour 2 eggs Flour (1 kg bag) costs £1.00 Eggs (box of 10) cost £1.26 300 ml milk Milk (1 litre bottle) costs 90p 1 lemon Lemons (bag of 3) cost £1.00 How much would it cost to make 50 pancakes? Give your answer to the nearest penny. -
The Universe
The Universe N.G. Schultheiss translated and adapted by K. Schadenberg 1 Introduction This module ‘The Universe’ follows on the module ‘The Sky’ and can give you some inspiration for the use of your own telescope (see module series leading to ‘Telescopes’). 2 Man as measure of things When looking at the world around us we look at it with a human measure. We express size in a familiar unit; the metre or foot. A man is roughly 6 feet tall. We can easily imagine how large a metre is. The same is true for other common units; the litre, the second, etc. But when looking at ‘worlds’ much larger or smaller than our every day world these human measures begin to fail. Can you imagine the length of a light year? Or the duration of a nanosecond? Below is a small table which lists common length scales and the objects which can comfortably be expressed using these units: Unit Object Organism mm: millimetre grain of sand cm: centimetre rubber (eraser) fly, grass dm: decimetre pen, paper rabbit, sunflower m: metre furniture, bicycle human, shrub dm: decametre house, bus whale, tree hm: hectometre street, ship km: kilometre village, city Table 1: Different length scales. Going down in the table, everything becomes a factor 10 larger. Going up the opposite happens, every- thing becomes a factor 10 smaller. Using this table we see that a city is roughly 1,000,000 times larger than a grain of sand. A rather large number. This is why different units can be convenient, smaller number are easier to understand.