Linear Functions. Definition. Suppose V and W Are Vector Spaces and L
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Research Brief March 2017 Publication #2017-16
Research Brief March 2017 Publication #2017-16 Flourishing From the Start: What Is It and How Can It Be Measured? Kristin Anderson Moore, PhD, Child Trends Christina D. Bethell, PhD, The Child and Adolescent Health Measurement Introduction Initiative, Johns Hopkins Bloomberg School of Every parent wants their child to flourish, and every community wants its Public Health children to thrive. It is not sufficient for children to avoid negative outcomes. Rather, from their earliest years, we should foster positive outcomes for David Murphey, PhD, children. Substantial evidence indicates that early investments to foster positive child development can reap large and lasting gains.1 But in order to Child Trends implement and sustain policies and programs that help children flourish, we need to accurately define, measure, and then monitor, “flourishing.”a Miranda Carver Martin, BA, Child Trends By comparing the available child development research literature with the data currently being collected by health researchers and other practitioners, Martha Beltz, BA, we have identified important gaps in our definition of flourishing.2 In formerly of Child Trends particular, the field lacks a set of brief, robust, and culturally sensitive measures of “thriving” constructs critical for young children.3 This is also true for measures of the promotive and protective factors that contribute to thriving. Even when measures do exist, there are serious concerns regarding their validity and utility. We instead recommend these high-priority measures of flourishing -

Ligature Modeling for Recognition of Characters Written in 3D Space Dae Hwan Kim, Jin Hyung Kim
Ligature Modeling for Recognition of Characters Written in 3D Space Dae Hwan Kim, Jin Hyung Kim To cite this version: Dae Hwan Kim, Jin Hyung Kim. Ligature Modeling for Recognition of Characters Written in 3D Space. Tenth International Workshop on Frontiers in Handwriting Recognition, Université de Rennes 1, Oct 2006, La Baule (France). inria-00105116 HAL Id: inria-00105116 https://hal.inria.fr/inria-00105116 Submitted on 10 Oct 2006 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Ligature Modeling for Recognition of Characters Written in 3D Space Dae Hwan Kim Jin Hyung Kim Artificial Intelligence and Artificial Intelligence and Pattern Recognition Lab. Pattern Recognition Lab. KAIST, Daejeon, KAIST, Daejeon, South Korea South Korea [email protected] [email protected] Abstract defined shape of character while it showed high recognition performance. Moreover when a user writes In this work, we propose a 3D space handwriting multiple stroke character such as ‘4’, the user has to recognition system by combining 2D space handwriting write a new shape which is predefined in a uni-stroke models and 3D space ligature models based on that the and which he/she has never seen. -
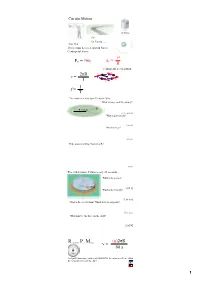
FC = Mac V2 R V = 2Πr T F = T 1
Circular Motion Gravitron Cars Car Turning (has a curse) Rope Skip There must be a net inward force: Centripetal Force v2 F = maC a = C C R Centripetal acceleration 2πR v v v = R v T v 1 f = T The motorcycle rider does 13 laps in 150 s. What is his period? Frequency? R = 30 m [11.5 s, 0.087 Hz] What is his velocity? [16.3 m/s] What is his aC? [8.9 m/s2] If the mass is 180 kg, what is his FC? [1600 N] The child rotates 5 times every 22 seconds... What is the period? 60 kg [4.4 s] What is the velocity? [2.86 m/s] What is the acceleration? Which way does it point? [4.1 m/s2] What must be the force on the child? [245 N] Revolutions Per Minute (n)2πR v = 60 s An Ipod's hard drive rotates at 4200 RPM. Its radius is 0.03 m. What is the velocity in m/s of its edge? 1 Airplane Turning v = 232 m/s (520 mph) aC = 7 g's What is the turn radius? [785 m = 2757 ft] 2 FC Solving Circular Motion Problems 1. Determine FC (FBD) 2 2. Set FC = m v R 3. Solve for unknowns The book's mass is 2 kg it is spun so that the tension is 45 N. What is the velocity of the book in m/s? In RPM? R = 0.75 m [4.11 m/s] [52 RPM] What is the period (T) of the book? [1.15 s] The car is traveling at 25 m/s and the turn's radius is 63 m. -

ISO Basic Latin Alphabet
ISO basic Latin alphabet The ISO basic Latin alphabet is a Latin-script alphabet and consists of two sets of 26 letters, codified in[1] various national and international standards and used widely in international communication. The two sets contain the following 26 letters each:[1][2] ISO basic Latin alphabet Uppercase Latin A B C D E F G H I J K L M N O P Q R S T U V W X Y Z alphabet Lowercase Latin a b c d e f g h i j k l m n o p q r s t u v w x y z alphabet Contents History Terminology Name for Unicode block that contains all letters Names for the two subsets Names for the letters Timeline for encoding standards Timeline for widely used computer codes supporting the alphabet Representation Usage Alphabets containing the same set of letters Column numbering See also References History By the 1960s it became apparent to thecomputer and telecommunications industries in the First World that a non-proprietary method of encoding characters was needed. The International Organization for Standardization (ISO) encapsulated the Latin script in their (ISO/IEC 646) 7-bit character-encoding standard. To achieve widespread acceptance, this encapsulation was based on popular usage. The standard was based on the already published American Standard Code for Information Interchange, better known as ASCII, which included in the character set the 26 × 2 letters of the English alphabet. Later standards issued by the ISO, for example ISO/IEC 8859 (8-bit character encoding) and ISO/IEC 10646 (Unicode Latin), have continued to define the 26 × 2 letters of the English alphabet as the basic Latin script with extensions to handle other letters in other languages.[1] Terminology Name for Unicode block that contains all letters The Unicode block that contains the alphabet is called "C0 Controls and Basic Latin". -

Form W-4, Employee's Withholding Certificate
Employee’s Withholding Certificate OMB No. 1545-0074 Form W-4 ▶ (Rev. December 2020) Complete Form W-4 so that your employer can withhold the correct federal income tax from your pay. ▶ Department of the Treasury Give Form W-4 to your employer. 2021 Internal Revenue Service ▶ Your withholding is subject to review by the IRS. Step 1: (a) First name and middle initial Last name (b) Social security number Enter Address ▶ Does your name match the Personal name on your social security card? If not, to ensure you get Information City or town, state, and ZIP code credit for your earnings, contact SSA at 800-772-1213 or go to www.ssa.gov. (c) Single or Married filing separately Married filing jointly or Qualifying widow(er) Head of household (Check only if you’re unmarried and pay more than half the costs of keeping up a home for yourself and a qualifying individual.) Complete Steps 2–4 ONLY if they apply to you; otherwise, skip to Step 5. See page 2 for more information on each step, who can claim exemption from withholding, when to use the estimator at www.irs.gov/W4App, and privacy. Step 2: Complete this step if you (1) hold more than one job at a time, or (2) are married filing jointly and your spouse Multiple Jobs also works. The correct amount of withholding depends on income earned from all of these jobs. or Spouse Do only one of the following. Works (a) Use the estimator at www.irs.gov/W4App for most accurate withholding for this step (and Steps 3–4); or (b) Use the Multiple Jobs Worksheet on page 3 and enter the result in Step 4(c) below for roughly accurate withholding; or (c) If there are only two jobs total, you may check this box. -

Ffontiau Cymraeg
This publication is available in other languages and formats on request. Mae'r cyhoeddiad hwn ar gael mewn ieithoedd a fformatau eraill ar gais. [email protected] www.caerphilly.gov.uk/equalities How to type Accented Characters This guidance document has been produced to provide practical help when typing letters or circulars, or when designing posters or flyers so that getting accents on various letters when typing is made easier. The guide should be used alongside the Council’s Guidance on Equalities in Designing and Printing. Please note this is for PCs only and will not work on Macs. Firstly, on your keyboard make sure the Num Lock is switched on, or the codes shown in this document won’t work (this button is found above the numeric keypad on the right of your keyboard). By pressing the ALT key (to the left of the space bar), holding it down and then entering a certain sequence of numbers on the numeric keypad, it's very easy to get almost any accented character you want. For example, to get the letter “ô”, press and hold the ALT key, type in the code 0 2 4 4, then release the ALT key. The number sequences shown from page 3 onwards work in most fonts in order to get an accent over “a, e, i, o, u”, the vowels in the English alphabet. In other languages, for example in French, the letter "c" can be accented and in Spanish, "n" can be accented too. Many other languages have accents on consonants as well as vowels. -

Gerard Manley Hopkins' Diacritics: a Corpus Based Study
Gerard Manley Hopkins’ Diacritics: A Corpus Based Study by Claire Moore-Cantwell This is my difficulty, what marks to use and when to use them: they are so much needed, and yet so objectionable.1 ~Hopkins 1. Introduction In a letter to his friend Robert Bridges, Hopkins once wrote: “... my apparent licences are counterbalanced, and more, by my strictness. In fact all English verse, except Milton’s, almost, offends me as ‘licentious’. Remember this.”2 The typical view held by modern critics can be seen in James Wimsatt’s 2006 volume, as he begins his discussion of sprung rhythm by saying, “For Hopkins the chief advantage of sprung rhythm lies in its bringing verse rhythms closer to natural speech rhythms than traditional verse systems usually allow.”3 In a later chapter, he also states that “[Hopkins’] stress indicators mark ‘actual stress’ which is both metrical and sense stress, part of linguistic meaning broadly understood to include feeling.” In his 1989 article, Sprung Rhythm, Kiparsky asks the question “Wherein lies [sprung rhythm’s] unique strictness?” In answer to this question, he proposes a system of syllable quantity coupled with a set of metrical rules by which, he claims, all of Hopkins’ verse is metrical, but other conceivable lines are not. This paper is an outgrowth of a larger project (Hayes & Moore-Cantwell in progress) in which Kiparsky’s claims are being analyzed in greater detail. In particular, we believe that Kiparsky’s system overgenerates, allowing too many different possible scansions for each line for it to be entirely falsifiable. The goal of the project is to tighten Kiparsky’s system by taking into account the gradience that can be found in metrical well-formedness, so that while many different scansion of a line may be 1 Letter to Bridges dated 1 April 1885. -

Teresa Blackford V. Welborn Clinic
IN THE Indiana Supreme Court Supreme Court Case No. 21S-CT-85 Teresa Blackford Appellant (Plaintiff below) –v– Welborn Clinic Appellee (Defendant below) Argued: April 22, 2021 | Decided: August 31, 2021 Appeal from the Vanderburgh Circuit Court No. 82C01-1804-CT-2434 The Honorable David D. Kiely, Judge On Petition to Transfer from the Indiana Court of Appeals No. 19A-CT-2054 Opinion by Justice Goff Chief Justice Rush and Justices David, Massa, and Slaughter concur. Goff, Justice. Statutory limitations of action are “fundamental to a well-ordered judicial system.” See Bd. of Regents of Univ. of State of N. Y. v. Tomanio, 446 U.S. 478, 487 (1980). The process of discovery and trial, revealing ultimate facts that either help or harm the plaintiff, are “obviously more reliable if the witness or testimony in question is relatively fresh.” Id. And potential defendants, of course, seek to avoid indefinite liability for past conduct. C. Corman, 1 Limitation of Actions § 1.1, at 5 (1991). Naturally, then, “there comes a point at which the delay of a plaintiff in asserting a claim is sufficiently likely either to impair the accuracy of the fact-finding process or to upset settled expectations that a substantive claim will be barred” regardless of its merit. Tomanio, 446 U.S. at 487. At the same time, most courts recognize that certain circumstances may “justify an exception to these strong policies of repose,” extending the time in which a plaintiff may file a claim—a process known as “tolling.” Id. at 487–88. The circumstances here present us with these competing interests: the plaintiff, having been misinformed of a medical diagnosis by her provider, which dissolved its business more than five years prior to the plaintiff filing her complaint, seeks relief for her injuries on grounds of fraudulent concealment, despite expiration of the applicable limitation period. -

Chapter 3 Motion in Two and Three Dimensions
Chapter 3 Motion in Two and Three Dimensions 3.1 The Important Stuff 3.1.1 Position In three dimensions, the location of a particle is specified by its location vector, r: r = xi + yj + zk (3.1) If during a time interval ∆t the position vector of the particle changes from r1 to r2, the displacement ∆r for that time interval is ∆r = r1 − r2 (3.2) = (x2 − x1)i +(y2 − y1)j +(z2 − z1)k (3.3) 3.1.2 Velocity If a particle moves through a displacement ∆r in a time interval ∆t then its average velocity for that interval is ∆r ∆x ∆y ∆z v = = i + j + k (3.4) ∆t ∆t ∆t ∆t As before, a more interesting quantity is the instantaneous velocity v, which is the limit of the average velocity when we shrink the time interval ∆t to zero. It is the time derivative of the position vector r: dr v = (3.5) dt d = (xi + yj + zk) (3.6) dt dx dy dz = i + j + k (3.7) dt dt dt can be written: v = vxi + vyj + vzk (3.8) 51 52 CHAPTER 3. MOTION IN TWO AND THREE DIMENSIONS where dx dy dz v = v = v = (3.9) x dt y dt z dt The instantaneous velocity v of a particle is always tangent to the path of the particle. 3.1.3 Acceleration If a particle’s velocity changes by ∆v in a time period ∆t, the average acceleration a for that period is ∆v ∆v ∆v ∆v a = = x i + y j + z k (3.10) ∆t ∆t ∆t ∆t but a much more interesting quantity is the result of shrinking the period ∆t to zero, which gives us the instantaneous acceleration, a. -

Driquik W/R VOC
Driquik™ W/R VOC DTM PRODUCT DATA SHEET SELECTION & SPECIFICATION DATA Generic Type PVA / Acrylic Latex One component, water based, low VOC, low gloss, Direct to Metal (DTM) acrylic latex coating that Description provides an excellent moisture barrier. • Excellent water resistance • Low VOC • Easy one coat coverage • Excellent adhesion to metal Features • Resistant to spillage /splash of mild chemical • Flexible • Very fast dry • Heat Resistant Color Black or per customer requirements Finish Flat 3 - 5 mils (76 - 127 microns) single coat Dry Film Thickness Not to exceed 10 mils (250 µm) DFT Solids Content By Volume 39% +/- 3% 626 ft²/gal at 1.0 mils (15.4 m²/l at 25 microns) Theoretical Coverage 209 ft²/gal at 3.0 mils (5.1 m²/l at 75 microns) Rate 125 ft²/gal at 5.0 mils (3.1 m²/l at 125 microns) Allow for loss in mixing and application. As Supplied : 0 VOC Values Calculated SUBSTRATES & SURFACE PREPARATION General Designed to be applied direct to metal in a single or two coat application. Severe service applications – blasted to SSPC-SP-10 to a 1.5-2.5 mil angular profile Steel Lesser service applications – blasted to SSPC-SP-6 Surface to be free of all looser rust, dirt, grease and other contaminants Aluminum Remove all surface contaminants and treat with Strathmore’s Wash Primer or equivalent September 2020 113S Page 1 of 3 Driquik™ W/R VOC DTM PRODUCT DATA SHEET PERFORMANCE DATA All test data was generated under laboratory conditions. Field testing results may vary. Test Method System Results Adhesion (ASTM D3359) Driquik W/R VOC DTM 5B Conical Mandrel Flexibility (ASTM D522) Driquik W/R VOC DTM Passes 1/8" Hardness (ASTM D3363) Driquik W/R VOC DTM 3B 5 hrs @ 400°F (204°C) Heat Resistance Driquik W/R VOC DTM for two consecutive days Humidity Resistance (ASTM D4585) Driquik W/R VOC DTM >2000 hrs Up to 120 lbs.in (Direct) Impact Resistance (ASTM D2794) Driquik W/R VOC DTM 60 lbs. -

Alphabets, Letters and Diacritics in European Languages (As They Appear in Geography)
1 Vigleik Leira (Norway): [email protected] Alphabets, Letters and Diacritics in European Languages (as they appear in Geography) To the best of my knowledge English seems to be the only language which makes use of a "clean" Latin alphabet, i.d. there is no use of diacritics or special letters of any kind. All the other languages based on Latin letters employ, to a larger or lesser degree, some diacritics and/or some special letters. The survey below is purely literal. It has nothing to say on the pronunciation of the different letters. Information on the phonetic/phonemic values of the graphic entities must be sought elsewhere, in language specific descriptions. The 26 letters a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z may be considered the standard European alphabet. In this article the word diacritic is used with this meaning: any sign placed above, through or below a standard letter (among the 26 given above); disregarding the cases where the resulting letter (e.g. å in Norwegian) is considered an ordinary letter in the alphabet of the language where it is used. Albanian The alphabet (36 letters): a, b, c, ç, d, dh, e, ë, f, g, gj, h, i, j, k, l, ll, m, n, nj, o, p, q, r, rr, s, sh, t, th, u, v, x, xh, y, z, zh. Missing standard letter: w. Letters with diacritics: ç, ë. Sequences treated as one letter: dh, gj, ll, rr, sh, th, xh, zh. -
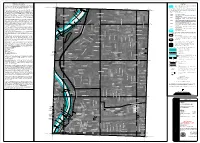
Map 5 South Riverfront
! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! NOTES TO USERS ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! LEGEND ! ! ! ! ! ! ! ! ! ! ! ! ! !