Ligature Modeling for Recognition of Characters Written in 3D Space Dae Hwan Kim, Jin Hyung Kim
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Research Brief March 2017 Publication #2017-16
Research Brief March 2017 Publication #2017-16 Flourishing From the Start: What Is It and How Can It Be Measured? Kristin Anderson Moore, PhD, Child Trends Christina D. Bethell, PhD, The Child and Adolescent Health Measurement Introduction Initiative, Johns Hopkins Bloomberg School of Every parent wants their child to flourish, and every community wants its Public Health children to thrive. It is not sufficient for children to avoid negative outcomes. Rather, from their earliest years, we should foster positive outcomes for David Murphey, PhD, children. Substantial evidence indicates that early investments to foster positive child development can reap large and lasting gains.1 But in order to Child Trends implement and sustain policies and programs that help children flourish, we need to accurately define, measure, and then monitor, “flourishing.”a Miranda Carver Martin, BA, Child Trends By comparing the available child development research literature with the data currently being collected by health researchers and other practitioners, Martha Beltz, BA, we have identified important gaps in our definition of flourishing.2 In formerly of Child Trends particular, the field lacks a set of brief, robust, and culturally sensitive measures of “thriving” constructs critical for young children.3 This is also true for measures of the promotive and protective factors that contribute to thriving. Even when measures do exist, there are serious concerns regarding their validity and utility. We instead recommend these high-priority measures of flourishing -

Manual LEIBINGER JET2 Neo
Manual LEIBINGER JET2 neo Release R1.00e Group 1 Table of contents Page 1 1.1 Table of contents 1.1 Table of contents ..........................................................................................................1 1.2 Group directory.............................................................................................................9 1.3 Publisher.....................................................................................................................10 1.4 Introduction.................................................................................................................12 1.5 Document information.................................................................................................13 1.6 Guarantee...................................................................................................................13 2. Safety ..............................................................................................................................14 2.1 Dangers......................................................................................................................14 2.2 Safety instructions and recommendations...................................................................14 2.3 Intended use...............................................................................................................16 2.4 Safety sticker ..............................................................................................................17 2.5 Operating staff ............................................................................................................18 -

The Origin of the Peculiarities of the Vietnamese Alphabet André-Georges Haudricourt
The origin of the peculiarities of the Vietnamese alphabet André-Georges Haudricourt To cite this version: André-Georges Haudricourt. The origin of the peculiarities of the Vietnamese alphabet. Mon-Khmer Studies, 2010, 39, pp.89-104. halshs-00918824v2 HAL Id: halshs-00918824 https://halshs.archives-ouvertes.fr/halshs-00918824v2 Submitted on 17 Dec 2013 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Published in Mon-Khmer Studies 39. 89–104 (2010). The origin of the peculiarities of the Vietnamese alphabet by André-Georges Haudricourt Translated by Alexis Michaud, LACITO-CNRS, France Originally published as: L’origine des particularités de l’alphabet vietnamien, Dân Việt Nam 3:61-68, 1949. Translator’s foreword André-Georges Haudricourt’s contribution to Southeast Asian studies is internationally acknowledged, witness the Haudricourt Festschrift (Suriya, Thomas and Suwilai 1985). However, many of Haudricourt’s works are not yet available to the English-reading public. A volume of the most important papers by André-Georges Haudricourt, translated by an international team of specialists, is currently in preparation. Its aim is to share with the English- speaking academic community Haudricourt’s seminal publications, many of which address issues in Southeast Asian languages, linguistics and social anthropology. -

Daniel O'connell
Daniel O’Connell 708 Hoover St., Norman OK 73072 (405) 820-6218 – [email protected] EDUCATION ACCELERATED DUAL DEGREE PROGRAM: Completing Petroleum Engineering undergraduate Degree and an MBA concurrently Michael F. Price College of Business, University of Oklahoma Norman, OK Master of Business Administration; GPA: 4.0/4.0 May 2018 Training the Street; Two-Day Financial Modeling Seminar Mewbourne College of Earth and Energy, University of Oklahoma Norman, OK Bachelor of Science in Petroleum Engineering; GPA: 3.4/4.0 May 2018 EXPERIENCE May 2017- Gulfport Energy Oklahoma City, OK August 2017 Reservoir Engineering, (Internship) Forecasted oil, gas, and water production and revenues for all PDP wells within ARIES Quantified the effect of compression and spacing on already producing wells Created a water type-curve lookup table within ARIES, based on correlations found in Spotfire, to be used in water production forecasting for new wells drilled in the Utica January 2017- OU Center for Creation of Economic Wealth (CCEW) Norman, OK May 2017 Oklahoma Funding Accelerator Consulting Associate (Internship) Semester-long internship working closely with local Oklahoma City startup, SendARide, on business model generation, business plan creation, financial projections, and loan proposal preparation Researched and suggested top priority candidates for adoption of the SendARide app Explored healthcare regulations for possible limitations and opportunities for success May 2016- LINN Energy Agua Dulce, TX August 2016 Production Engineering, -

Desktop + Mobile Style Guide 06.22.15
DESKTOP + MOBILE STYLE GUIDE 06.22.15 SITE BASICS PRIMARY TYPEFACE PRIMARY COLORS SECONDARY COLORS Helvetica, Arial, sans-serif R0 G70 B127 R0 G24 B46 HEX# 00467F HEX# 00182E R255 G201 B57 R47 G107 B189 HEX# FFC939 HEX# 2F6BBD R77 G79 B83 HEX# 4D4F53 R0 G0 B0 HEX# 000000 2 UNIVERSAL ELEMENTS PRIMARY BUTTONS LINKS CARETS IDLE ROLLOVER IDLE ROLLOVER ON CLEAN BACKGROUND PRIMARY NAVIGATION ON BUSY BACKGROUND IDLE ROLLOVER 3 HEADINGS AND LISTS A Font Family Helvetica, Arial, sans-serif B Font Family Helvetica, Arial, sans-serif Font Size 40px/48px Font Size 30px A Font Weight Bold Color #ffffff Color #000000 B C C Font Family Helvetica, Arial, sans-serif D Font Family Helvetica, Arial, sans-serif Font Weight Bold Font Size 24px/34px D Font Size 24px/34px Color #000000 Color #2F6BBD E E Font Family Helvetica, Arial, sans-serif F Font Family Helvetica, Arial, sans-serif Font Size 24px/34px Font Size 24px/34px F Color #000000 Color #000000 Margin-bottom 34px Margin-bottom 17px G Font Family Helvetica, Arial, sans-serif Font Size 24px/34px Color #000000 Margin-bottom 17px G 4 DESKTOP TYPOGRAPHY B A A Font Family Helvetica, Arial, sans-serif B Font Family Helvetica, Arial, sans-serif C Font Size 16px Font Size 16px Font Weight Bold Color #ffffff Color #cccccc Hover Underline Hover Underline C Font Family Helvetica, Arial, sans-serif D Font Family Helvetica, Arial, sans-serif Font Weight Bold Font Size 24px/30px D Font Size 22px/24px Color #000000 E Color #ffffff F E Font Family Helvetica, Arial, sans-serif F Font Family Helvetica, Arial, sans-serif -

ISO Basic Latin Alphabet
ISO basic Latin alphabet The ISO basic Latin alphabet is a Latin-script alphabet and consists of two sets of 26 letters, codified in[1] various national and international standards and used widely in international communication. The two sets contain the following 26 letters each:[1][2] ISO basic Latin alphabet Uppercase Latin A B C D E F G H I J K L M N O P Q R S T U V W X Y Z alphabet Lowercase Latin a b c d e f g h i j k l m n o p q r s t u v w x y z alphabet Contents History Terminology Name for Unicode block that contains all letters Names for the two subsets Names for the letters Timeline for encoding standards Timeline for widely used computer codes supporting the alphabet Representation Usage Alphabets containing the same set of letters Column numbering See also References History By the 1960s it became apparent to thecomputer and telecommunications industries in the First World that a non-proprietary method of encoding characters was needed. The International Organization for Standardization (ISO) encapsulated the Latin script in their (ISO/IEC 646) 7-bit character-encoding standard. To achieve widespread acceptance, this encapsulation was based on popular usage. The standard was based on the already published American Standard Code for Information Interchange, better known as ASCII, which included in the character set the 26 × 2 letters of the English alphabet. Later standards issued by the ISO, for example ISO/IEC 8859 (8-bit character encoding) and ISO/IEC 10646 (Unicode Latin), have continued to define the 26 × 2 letters of the English alphabet as the basic Latin script with extensions to handle other letters in other languages.[1] Terminology Name for Unicode block that contains all letters The Unicode block that contains the alphabet is called "C0 Controls and Basic Latin". -

Form W-4, Employee's Withholding Certificate
Employee’s Withholding Certificate OMB No. 1545-0074 Form W-4 ▶ (Rev. December 2020) Complete Form W-4 so that your employer can withhold the correct federal income tax from your pay. ▶ Department of the Treasury Give Form W-4 to your employer. 2021 Internal Revenue Service ▶ Your withholding is subject to review by the IRS. Step 1: (a) First name and middle initial Last name (b) Social security number Enter Address ▶ Does your name match the Personal name on your social security card? If not, to ensure you get Information City or town, state, and ZIP code credit for your earnings, contact SSA at 800-772-1213 or go to www.ssa.gov. (c) Single or Married filing separately Married filing jointly or Qualifying widow(er) Head of household (Check only if you’re unmarried and pay more than half the costs of keeping up a home for yourself and a qualifying individual.) Complete Steps 2–4 ONLY if they apply to you; otherwise, skip to Step 5. See page 2 for more information on each step, who can claim exemption from withholding, when to use the estimator at www.irs.gov/W4App, and privacy. Step 2: Complete this step if you (1) hold more than one job at a time, or (2) are married filing jointly and your spouse Multiple Jobs also works. The correct amount of withholding depends on income earned from all of these jobs. or Spouse Do only one of the following. Works (a) Use the estimator at www.irs.gov/W4App for most accurate withholding for this step (and Steps 3–4); or (b) Use the Multiple Jobs Worksheet on page 3 and enter the result in Step 4(c) below for roughly accurate withholding; or (c) If there are only two jobs total, you may check this box. -

Ffontiau Cymraeg
This publication is available in other languages and formats on request. Mae'r cyhoeddiad hwn ar gael mewn ieithoedd a fformatau eraill ar gais. [email protected] www.caerphilly.gov.uk/equalities How to type Accented Characters This guidance document has been produced to provide practical help when typing letters or circulars, or when designing posters or flyers so that getting accents on various letters when typing is made easier. The guide should be used alongside the Council’s Guidance on Equalities in Designing and Printing. Please note this is for PCs only and will not work on Macs. Firstly, on your keyboard make sure the Num Lock is switched on, or the codes shown in this document won’t work (this button is found above the numeric keypad on the right of your keyboard). By pressing the ALT key (to the left of the space bar), holding it down and then entering a certain sequence of numbers on the numeric keypad, it's very easy to get almost any accented character you want. For example, to get the letter “ô”, press and hold the ALT key, type in the code 0 2 4 4, then release the ALT key. The number sequences shown from page 3 onwards work in most fonts in order to get an accent over “a, e, i, o, u”, the vowels in the English alphabet. In other languages, for example in French, the letter "c" can be accented and in Spanish, "n" can be accented too. Many other languages have accents on consonants as well as vowels. -
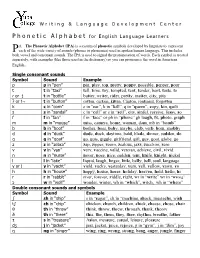
Writing & Language Development Center Phonetic Alphabet for English Language Learners Pin, Play, Top, Pretty, Poppy, Possibl
Writing & Language Development Center Phonetic Alphabet f o r English Language Learners A—The Phonetic Alphabet (IPA) is a system of phonetic symbols developed by linguists to represent P each of the wide variety of sounds (phones or phonemes) used in spoken human language. This includes both vowel and consonant sounds. The IPA is used to signal the pronunciation of words. Each symbol is treated separately, with examples (like those used in the dictionary) so you can pronounce the word in American English. Single consonant sounds Symbol Sound Example p p in “pen” pin, play, top, pretty, poppy, possible, pepper, pour t t in “taxi” tell, time, toy, tempted, tent, tender, bent, taste, to ɾ or ţ t in “bottle” butter, writer, rider, pretty, matter, city, pity ʔ or t¬ t in “button” cotton, curtain, kitten, Clinton, continent, forgotten k c in “corn” c in “car”, k in “kill”, q in “queen”, copy, kin, quilt s s in “sandal” c in “cell” or s in “sell”, city, sinful, receive, fussy, so f f in “fan” f in “face” or ph in “phone” gh laugh, fit, photo, graph m m in “mouse” miss, camera, home, woman, dam, mb in “bomb” b b in “boot” bother, boss, baby, maybe, club, verb, born, snobby d d in “duck” dude, duck, daytime, bald, blade, dinner, sudden, do g g in “goat” go, guts, giggle, girlfriend, gift, guy, goat, globe, go z z in “zebra” zap, zipper, zoom, zealous, jazz, zucchini, zero v v in “van” very, vaccine, valid, veteran, achieve, civil, vivid n n in “nurse” never, nose, nice, sudden, tent, knife, knight, nickel l l in “lake” liquid, laugh, linger, -

Gerard Manley Hopkins' Diacritics: a Corpus Based Study
Gerard Manley Hopkins’ Diacritics: A Corpus Based Study by Claire Moore-Cantwell This is my difficulty, what marks to use and when to use them: they are so much needed, and yet so objectionable.1 ~Hopkins 1. Introduction In a letter to his friend Robert Bridges, Hopkins once wrote: “... my apparent licences are counterbalanced, and more, by my strictness. In fact all English verse, except Milton’s, almost, offends me as ‘licentious’. Remember this.”2 The typical view held by modern critics can be seen in James Wimsatt’s 2006 volume, as he begins his discussion of sprung rhythm by saying, “For Hopkins the chief advantage of sprung rhythm lies in its bringing verse rhythms closer to natural speech rhythms than traditional verse systems usually allow.”3 In a later chapter, he also states that “[Hopkins’] stress indicators mark ‘actual stress’ which is both metrical and sense stress, part of linguistic meaning broadly understood to include feeling.” In his 1989 article, Sprung Rhythm, Kiparsky asks the question “Wherein lies [sprung rhythm’s] unique strictness?” In answer to this question, he proposes a system of syllable quantity coupled with a set of metrical rules by which, he claims, all of Hopkins’ verse is metrical, but other conceivable lines are not. This paper is an outgrowth of a larger project (Hayes & Moore-Cantwell in progress) in which Kiparsky’s claims are being analyzed in greater detail. In particular, we believe that Kiparsky’s system overgenerates, allowing too many different possible scansions for each line for it to be entirely falsifiable. The goal of the project is to tighten Kiparsky’s system by taking into account the gradience that can be found in metrical well-formedness, so that while many different scansion of a line may be 1 Letter to Bridges dated 1 April 1885. -
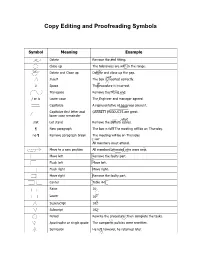
Copy Editing and Proofreading Symbols
Copy Editing and Proofreading Symbols Symbol Meaning Example Delete Remove the end fitting. Close up The tolerances are with in the range. Delete and Close up Deltete and close up the gap. not Insert The box is inserted correctly. # # Space Theprocedure is incorrect. Transpose Remove the fitting end. / or lc Lower case The Engineer and manager agreed. Capitalize A representative of nasa was present. Capitalize first letter and GARRETT PRODUCTS are great. lower case remainder stet stet Let stand Remove the battery cables. ¶ New paragraph The box is full. The meeting will be on Thursday. no ¶ Remove paragraph break The meeting will be on Thursday. no All members must attend. Move to a new position All members attended who were new. Move left Remove the faulty part. Flush left Move left. Flush right Move right. Move right Remove the faulty part. Center Table 4-1 Raise 162 Lower 162 Superscript 162 Subscript 162 . Period Rewrite the procedure. Then complete the tasks. ‘ ‘ Apostrophe or single quote The companys policies were rewritten. ; Semicolon He left however, he returned later. ; Symbol Meaning Example Colon There were three items nuts, bolts, and screws. : : , Comma Apply pressure to the first second and third bolts. , , -| Hyphen A valuable byproduct was created. sp Spell out The info was incorrect. sp Abbreviate The part was twelve feet long. || or = Align Personnel Facilities Equipment __________ Underscore The part was listed under Electrical. Run in with previous line He rewrote the pages and went home. Em dash It was the beginning so I thought. En dash The value is 120 408. -

Classifying Type Thunder Graphics Training • Type Workshop Typeface Groups
Classifying Type Thunder Graphics Training • Type Workshop Typeface Groups Cla sifying Type Typeface Groups The typefaces you choose can make or break a layout or design because they set the tone of the message.Choosing The the more right you font know for the about job is type, an important the better design your decision.type choices There will are be. so many different fonts available for the computer that it would be almost impossible to learn the names of every one. However, manys typefaces share similar qualities. Typographers classify fonts into groups to help Typographers classify type into groups to help remember the different kinds. Often, a font from within oneremember group can the be different substituted kinds. for Often, one nota font available from within to achieve one group the samecan be effect. substituted Different for anothertypographers usewhen different not available groupings. to achieve The classifi the samecation effect. system Different used by typographers Thunder Graphics use different includes groups. seven The major groups.classification system used byStevenson includes seven major groups. Use the Right arrow key to move to the next page. • Use the Left arrow key to move back a page. Use the key combination, Command (⌘) + Q to quit the presentation. Thunder Graphics Training • Type Workshop Typeface Groups ����������������������� ��������������������������������������������������������������������������������� ���������������������������������������������������������������������������� ������������������������������������������������������������������������������