DOCSLIB.ORG

Teresa Blackford V. Welborn Clinic

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Teresa Blackford V. Welborn Clinic IN THE Indiana Supreme Court Supreme Court Case No. 21S-CT-85 Teresa Blackford Appellant (Plaintiff below) –v– Welborn Clinic Appellee (Defendant below) Argued: April 22, 2021 | Decided: August 31, 2021 Appeal from the Vanderburgh Circuit Court No. 82C01-1804-CT-2434 The Honorable David D. Kiely, Judge On Petition to Transfer from the Indiana Court of Appeals No. 19A-CT-2054 Opinion by Justice Goff Chief Justice Rush and Justices David, Massa, and Slaughter concur. Goff, Justice. Statutory limitations of action are “fundamental to a well-ordered judicial system.” See Bd. of Regents of Univ. of State of N. Y. v. Tomanio, 446 U.S. 478, 487 (1980). The process of discovery and trial, revealing ultimate facts that either help or harm the plaintiff, are “obviously more reliable if the witness or testimony in question is relatively fresh.” Id. And potential defendants, of course, seek to avoid indefinite liability for past conduct. C. Corman, 1 Limitation of Actions § 1.1, at 5 (1991). Naturally, then, “there comes a point at which the delay of a plaintiff in asserting a claim is sufficiently likely either to impair the accuracy of the fact-finding process or to upset settled expectations that a substantive claim will be barred” regardless of its merit. Tomanio, 446 U.S. at 487. At the same time, most courts recognize that certain circumstances may “justify an exception to these strong policies of repose,” extending the time in which a plaintiff may file a claim—a process known as “tolling.” Id. at 487–88. The circumstances here present us with these competing interests: the plaintiff, having been misinformed of a medical diagnosis by her provider, which dissolved its business more than five years prior to the plaintiff filing her complaint, seeks relief for her injuries on grounds of fraudulent concealment, despite expiration of the applicable limitation period. Because we consider the limitation period at issue a statute of repose (rather than a general statute of limitation or non-claim statute), we conclude that fraudulent concealment may not extend the time in which to file a claim. And even if the limitation period were subject to tolling, the defendant’s constructive fraud precludes equitable relief. For these Indiana Supreme Court | Case No. 21S-CT-85 | August 31, 2021 Page 2 of 18 reasons, we hold that the plaintiff’s claim is untimely.1 As such, we affirm the trial court’s order granting summary judgment to the defendant and denying the plaintiff’s motion for partial summary judgment. Facts and Procedural History In 2003, the Welborn Clinic (or, the Clinic) tested Teresa Blackford for hepatitis, a known cause of a skin condition from which she suffered at the time. Upon completing the test, the Clinic informed Blackford that the results were negative. For the next several years, Blackford continued to receive treatment for her skin condition from the Clinic. But on June 30, 2009, the Clinic, under the Indiana Business Trust Act (IBTA or Act), surrendered its authority to conduct business in the state, effectively terminating its relationship with Blackford. In 2014, as Blackford’s health declined, her new doctor diagnosed her with hepatitis. This diagnosis prompted Blackford to request her medical records from the Clinic, which revealed that she had in fact tested positive for hepatitis in 2003. Though treated for her condition by her new doctor, Blackford had developed cirrhosis of the liver because of the delay in treatment, exposing her to a heightened risk of other medical problems. Upon discovering the original test results, Blackford, on March 13, 2015, sued for medical malpractice—first with the Indiana Department of Insurance and then in the trial court. At trial, the Clinic moved for summary judgment, arguing that, because Blackford sued more than five years after the Clinic dissolved, the IBTA time-barred her claim. See Ind. 1 The Indiana Trial Lawyers Association (ITLA) raises a separate constitutional claim in its amicus brief, arguing that the Indiana Business Trust Act, as applied to Blackford, violates the Privileges and Immunities Clause and the Open Courts Clause of the Indiana Constitution. ITLA, however, as amicus, could not raise a new claim that the parties failed to raise. ITLA is not a party on appeal. See Ind. Appellate Rule 17(A). And it is well established that “[a]n amicus is not permitted to raise new questions but rather must accept the case as it finds it at the time of its petition to intervene.” Indiana Dep’t of Transportation v. FMG Indianapolis, LLC, 167 N.E.3d 321, 333 (Ind. Ct. App. 2021) (citing Anderson Fed’n of Tchrs., Loc. 519 v. Sch. City of Anderson, 252 Ind. 558, 254 N.E.2d 329 (1970)). Indiana Supreme Court | Case No. 21S-CT-85 | August 31, 2021 Page 3 of 18 Code § 23-5-1-11 (2018) (entitling a business trust to “prosecute and defend” all claims filed within a five-year period after the trust surrenders its authority to conduct business). Blackford responded by moving for partial summary judgment on the same issue, asserting that the Clinic fraudulently concealed her test results, thus equitably tolling the IBTA’s five-year limitation period. The trial court ruled for the Clinic. In a divided opinion, the Court of Appeals reversed. Blackford v. Welborn Clinic, 150 N.E.3d 687 (Ind. Ct. App. 2020). The majority held (1) that fraudulent concealment may, upon a sufficient showing of facts, toll the IBTA’s five-year limitation period; (2) that, as a matter of law, by giving Blackford inaccurate test results in 2003, and by designating no evidence to the contrary, the Clinic fraudulently concealed—passively, if not actively—material medical information; and (3) that, by investigating her condition after termination of the doctor-patient relationship “in a reasonably diligent manner,” Blackford filed a timely complaint under the IBTA. Id. at 696–97. The dissent, however, would have affirmed the trial court on grounds of Blackford’s untimeliness in filing the complaint, reasoning that, while the discovery rule applies to active fraud, passive (or constructive) fraud, as Blackford alleged here, tolls the limitations period only “‘until the termination of the physician-patient relationship.’” Id. at 697–98 (Brown, J., dissenting) (quoting Boggs v. Tri-State Radiology, Inc., 730 N.E.2d 692, 698 (Ind. 2000)). We granted the Clinic’s petition for transfer, thus vacating the Court of Appeals opinion. See Ind. Appellate Rule 58(A). Standard of Review A de novo standard of review applies to summary-judgment rulings. Alldredge v. Good Samaritan Home, Inc., 9 N.E.3d 1257, 1259 (Ind. 2014). Under this standard, summary judgment is appropriate “if the designated evidentiary matter shows that there is no genuine issue as to any material fact and that the moving party is entitled to a judgment as a matter of law.” Ind. Trial Rule 56(C). Claims asserting a defense based on a statutory limitation period are particularly suitable for summary- Indiana Supreme Court | Case No. 21S-CT-85 | August 31, 2021 Page 4 of 18 judgment determination. See City of Marion v. London Witte Grp., LLC, 169 N.E.3d 382, 390 (Ind. 2021). “When a moving party asserts as an affirmative defense that an action is time-barred, and establishes that the action was commenced beyond the statutory period, the burden shifts to the nonmovant to establish an issue of fact material to a theory that avoids the defense.” Jurich v. John Crane, Inc., 824 N.E.2d 777, 780 (Ind. Ct. App. 2005). Discussion and Decision On transfer, the Clinic—joined by the Defense Trial Counsel of Indiana as amicus curiae—argues that, by its plain terms, the IBTA “creates a date certain after which all claims against it are barred.” Pet. to Trans. at 15. And to recognize an equitable exception for fraud, the Clinic contends, runs contrary to the IBTA’s plain language and to its purpose of shielding businesses from the need to defend against stale claims. Id. at 15–18. For her part, Blackford, along with amicus curiae the Indiana Trial Lawyers Association, maintains that the Clinic’s fraudulent concealment of her test results tolled the IBTA’s five-year limitation period. Legislative policy and principles of equity, she insists, prevent a party from exploiting another by fraudulent activity. Resp. to Trans. at 6. Simply put, she asserts, “[f]raud vitiates anything.” Id. To resolve this dispute, our decision proceeds in two parts. We first examine the various statutory limitations of action—general statutes of limitation, statutes of repose, and non-claim statutes—to determine whether the IBTA permits equitable tolling. Concluding that it does not, we then ask whether a limited exception applies in cases of fraudulent concealment—a question we likewise answer in the negative on grounds that the Clinic’s constructive fraud justifies no equitable relief for Blackford. Indiana Supreme Court | Case No. 21S-CT-85 | August 31, 2021 Page 5 of 18 I. The IBTA’s limitation period is not subject to equitable tolling. Enacted in 1963, the IBTA expressly recognizes a business trust—an unincorporated association in which one or more trustees engage in professional activities for the profit of its beneficiaries—as a type of organization permitted to conduct business in the state.2 Act of Mar. 14, 1963, ch. 353, §§ 2, 3, 1963 Ind. Acts 900, 901–02 (codified as amended at I.C. §§ 23-5-1-2, -3). When a business trust withdraws or “surrender[s]” its authority to conduct business, by filing a notice of intent with the secretary of state, the IBTA allows for a five-year winding-up period, during which the trust may “convey and dispose of its property and assets” and “perform any other act or acts pertinent to the liquidation of its business.” I.C.
Load more

Recommended publications
  • Research Brief March 2017 Publication #2017-16
    Research Brief March 2017 Publication #2017-16 Flourishing From the Start: What Is It and How Can It Be Measured? Kristin Anderson Moore, PhD, Child Trends Christina D. Bethell, PhD, The Child and Adolescent Health Measurement Introduction Initiative, Johns Hopkins Bloomberg School of Every parent wants their child to flourish, and every community wants its Public Health children to thrive. It is not sufficient for children to avoid negative outcomes. Rather, from their earliest years, we should foster positive outcomes for David Murphey, PhD, children. Substantial evidence indicates that early investments to foster positive child development can reap large and lasting gains.1 But in order to Child Trends implement and sustain policies and programs that help children flourish, we need to accurately define, measure, and then monitor, “flourishing.”a Miranda Carver Martin, BA, Child Trends By comparing the available child development research literature with the data currently being collected by health researchers and other practitioners, Martha Beltz, BA, we have identified important gaps in our definition of flourishing.2 In formerly of Child Trends particular, the field lacks a set of brief, robust, and culturally sensitive measures of “thriving” constructs critical for young children.3 This is also true for measures of the promotive and protective factors that contribute to thriving. Even when measures do exist, there are serious concerns regarding their validity and utility. We instead recommend these high-priority measures of flourishing
    [Show full text]
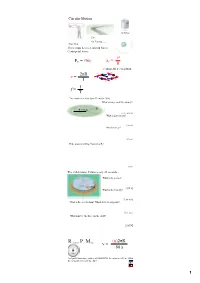
  • FC = Mac V2 R V = 2Πr T F = T 1
    Circular Motion Gravitron Cars Car Turning (has a curse) Rope Skip There must be a net inward force: Centripetal Force v2 F = maC a = C C R Centripetal acceleration 2πR v v v = R v T v 1 f = T The motorcycle rider does 13 laps in 150 s. What is his period? Frequency? R = 30 m [11.5 s, 0.087 Hz] What is his velocity? [16.3 m/s] What is his aC? [8.9 m/s2] If the mass is 180 kg, what is his FC? [1600 N] The child rotates 5 times every 22 seconds... What is the period? 60 kg [4.4 s] What is the velocity? [2.86 m/s] What is the acceleration? Which way does it point? [4.1 m/s2] What must be the force on the child? [245 N] Revolutions Per Minute (n)2πR v = 60 s An Ipod's hard drive rotates at 4200 RPM. Its radius is 0.03 m. What is the velocity in m/s of its edge? 1 Airplane Turning v = 232 m/s (520 mph) aC = 7 g's What is the turn radius? [785 m = 2757 ft] 2 FC Solving Circular Motion Problems 1. Determine FC (FBD) 2 2. Set FC = m v R 3. Solve for unknowns The book's mass is 2 kg it is spun so that the tension is 45 N. What is the velocity of the book in m/s? In RPM? R = 0.75 m [4.11 m/s] [52 RPM] What is the period (T) of the book? [1.15 s] The car is traveling at 25 m/s and the turn's radius is 63 m.
    [Show full text]
  • Chapter 3 Motion in Two and Three Dimensions
    Chapter 3 Motion in Two and Three Dimensions 3.1 The Important Stuff 3.1.1 Position In three dimensions, the location of a particle is specified by its location vector, r: r = xi + yj + zk (3.1) If during a time interval ∆t the position vector of the particle changes from r1 to r2, the displacement ∆r for that time interval is ∆r = r1 − r2 (3.2) = (x2 − x1)i +(y2 − y1)j +(z2 − z1)k (3.3) 3.1.2 Velocity If a particle moves through a displacement ∆r in a time interval ∆t then its average velocity for that interval is ∆r ∆x ∆y ∆z v = = i + j + k (3.4) ∆t ∆t ∆t ∆t As before, a more interesting quantity is the instantaneous velocity v, which is the limit of the average velocity when we shrink the time interval ∆t to zero. It is the time derivative of the position vector r: dr v = (3.5) dt d = (xi + yj + zk) (3.6) dt dx dy dz = i + j + k (3.7) dt dt dt can be written: v = vxi + vyj + vzk (3.8) 51 52 CHAPTER 3. MOTION IN TWO AND THREE DIMENSIONS where dx dy dz v = v = v = (3.9) x dt y dt z dt The instantaneous velocity v of a particle is always tangent to the path of the particle. 3.1.3 Acceleration If a particle’s velocity changes by ∆v in a time period ∆t, the average acceleration a for that period is ∆v ∆v ∆v ∆v a = = x i + y j + z k (3.10) ∆t ∆t ∆t ∆t but a much more interesting quantity is the result of shrinking the period ∆t to zero, which gives us the instantaneous acceleration, a.
    [Show full text]
  • Linear Functions. Definition. Suppose V and W Are Vector Spaces and L
    Linear functions. Definition. Suppose V and W are vector spaces and L : V → W. (Remember: This means that L is a function; the domain of L equals V ; and the range of L is a subset of W .) We say L is linear if L(cv) = cL(v) whenever c ∈ R and v ∈ V and L(v1 + v2) = L(v1) + L(v2) whenever v1, v2 ∈ V . We let ker L = {v ∈ V : L(v) = 0} and call ker L the kernel of L and we let rng L = {L(v): v ∈ V } so rng L is the range of L. We let L(V, W ) be the set of L such that L : V → W and L is linear. Example. Suppose m and n are positive integers and L ∈ L(Rn, Rm). For each i = 1, . , m and each j = 1, . , n we let i lj be the i-th component of L(ej). Thus Xm 1 m i L(ej) = (lj , . , lj ) = ljei whenever j = 1, . , n. i=1 n Suppose x = (x1, . , xn) ∈ R . Then Xn x = xjej j=1 so à ! 0 1 Xn Xn Xn Xn Xm Xm Xn i @ i A L(x) = L( xjej) = L(xjej) = xjL(ej) = xj ljei = xjlj ei. j=1 j=1 j=1 j=1 i=1 i=1 j=1 We call 2 1 1 1 3 l1 l2 ··· ln 6 7 6 2 1 2 7 6 l1 22 ··· ln 7 6 7 6 . .. 7 4 . 5 m m m l1 l2 ··· ln the standard matrix of L.
    [Show full text]
  • 1. Roman Numerals
    Chapter 1: Roman Numerals 1. Roman Numerals Introduction: In ancient Europe, people used some capital Roman letters to write numbers. Hence these numerals were known as Roman numerals. In this chapter, we will learn to write Roman numerals from 1 to 20. We see the use of Roman numerals in several clocks and watches, ancient European coins, books etc. Summative Assessment Let’s Study Symbols used for writing Roman numerals The three basic symbols used to write Roman numerals are given in the table below: Symbol used as Roman numeral I V X Numeric value represented by it 1 5 10 [Note: (1) There is no symbol for zero in Roman numerals. (2) The value of a symbol used for Roman numeral does not change with its place.] Rules for writing Roman numerals The rules for writing numbers from 1 to 20 using the Roman numerals are as follows: Rule 1: The number formed by writing the symbols I or X consecutively two or three times is the sum of the numeric values of the individual symbols. Examples: II = 1 + 1 = 2, III = 1 + 1 + 1 = 3, XX = 10 + 10 = 20 1 Std. V: Mathematics Rule 2: The consecutive repetition of symbols I and X is allowed for a maximum of three times to form a number. However, the symbol V is never repeated. Examples: (1) III = 3, however IIII ≠ 4 (2) XXX = 30, however XXXX ≠ 40 (3) VV ≠ 10 and VVV ≠ 15. Rule 3: When either I or V is written on the right side of the symbol of a bigger number, add its value to the value of the bigger number.
    [Show full text]
  • Proposal for Generation Panel for Latin Script Label Generation Ruleset for the Root Zone
    Generation Panel for Latin Script Label Generation Ruleset for the Root Zone Proposal for Generation Panel for Latin Script Label Generation Ruleset for the Root Zone Table of Contents 1. General Information 2 1.1 Use of Latin Script characters in domain names 3 1.2 Target Script for the Proposed Generation Panel 4 1.2.1 Diacritics 5 1.3 Countries with significant user communities using Latin script 6 2. Proposed Initial Composition of the Panel and Relationship with Past Work or Working Groups 7 3. Work Plan 13 3.1 Suggested Timeline with Significant Milestones 13 3.2 Sources for funding travel and logistics 16 3.3 Need for ICANN provided advisors 17 4. References 17 1 Generation Panel for Latin Script Label Generation Ruleset for the Root Zone 1. General Information The Latin script1 or Roman script is a major writing system of the world today, and the most widely used in terms of number of languages and number of speakers, with circa 70% of the world’s readers and writers making use of this script2 (Wikipedia). Historically, it is derived from the Greek alphabet, as is the Cyrillic script. The Greek alphabet is in turn derived from the Phoenician alphabet which dates to the mid-11th century BC and is itself based on older scripts. This explains why Latin, Cyrillic and Greek share some letters, which may become relevant to the ruleset in the form of cross-script variants. The Latin alphabet itself originated in Italy in the 7th Century BC. The original alphabet contained 21 upper case only letters: A, B, C, D, E, F, Z, H, I, K, L, M, N, O, P, Q, R, S, T, V and X.
    [Show full text]
  • V Codes (DSM-5) & Z Codes (ICD-10)
    V Codes (DSM-5) & Z Codes (ICD-10) Relational Problems V61.20 (Z62.820) Parent-Child Relational Problem V61.8 (Z62.891) Sibling Relational Problem V61.8 (Z62.29) Upbringing Away From Parents V61.29 (Z62.898) Child Affected by Parental Relationship Distress V61.10 (Z63.0) Relationship Distress With Spouse or Intimate Partner V61.03 (Z63.5) Disruption of Family by Separation or Divorce V61.8 (Z63.8) High Expressed Emotion Level Within Family V62.82 (Z63.4) Uncomplicated Bereavement Educational and Occupational Problems V62.3 (Z55.9) Academic or Educational Problem V62.21 (Z56.82) Problem Related to Current Military Deployment Status V62.29 (Z56.9) Other Problem Related to Employment Housing and Economic Problems V60.0 (Z59.0) Homelessness V60.1 (Z59.1) Inadequate Housing V60.89 (Z59.2) Discord With Neighbor, Lodger, or Landlord V60.6 (Z59.3) Problem Related to Living in a Residential Institution V60.2 (Z59.4) Lack of Adequate Food or Safe Drinking Water V60.2 (Z59.5) Extreme Poverty V60.2 (Z59.6) Low Income V60.2 (Z59.7) Insufficient Social Insurance or Welfare Support V60.9 (Z59.9) Unspecified Housing or Economic Problem Social Environment Other Problems Related to the Social Environment V62.89 (Z60.0) Phase of Life Problem V60.3 (Z60.2) Problem Related to Living Alone V62.4 (Z60.3) Acculturation Difficulty V62.4 (Z60.4) Social Exclusion or Rejection V62.4 (Z60.5) Target of (Perceived) Adverse Discrimination or Persecution V62.9 (Z60.9) Unspecified Problem Related to Social Environment Crime and Legal System Problems Related to Crime or
    [Show full text]
  • Let V Be an Inner Product Space, and Let W Be a Subspace of V with Orthogonal Basis = W1, W2, ..., Wn
    Definition 3.11: Let V be an inner product space, and let W be a subspace of V with orthogonal basis = w1, w2, ..., wn. For any u V , the orthogonal projection of u on W Bis { ∈ u, w u, w u, w proj u = 1 w + 2 w + + n w W w , w 1 w , w 2 ··· w , w n 1 1 2 2 n n and the component of u orthogonal to W is perp u = u proj u. W − W Theorem 3.12: Let V be an inner product space, and let W be a subspace of V . For any u V there exist unique vectors w W and w⊥ W ⊥ such that ∈ ∈ ∈ ⊥ u = w + w . ⊥ In particular, w = projW u and w = perpW u. 3 1 1 Example 3.3(c): For the matrix A = 1− 3 −1 and any u, v R3, we can define an inner product ⋄ −1 1− 3 ∈ − − 2 0 T 3 u, v = u Av on R . The vectors u1 = 1 and u2 = 3 are orthogonal in the resulting inner 1 1 4 − product space, so they form an orthogonal basis for a subspace W of R3. For the vector v = 5 , find 2 vectors w W and w⊥ W ⊥ such that v = w + w⊥. ∈ ∈ First we project v onto W to find w: 2 0 4 v, u1 v, u2 16 56 − w = projW v = u1 + u2 = − 1 + 3 = 5 . u1, u1 u2, u2 8 24 1 1 1 3 We then obtain 4 4 0 ⊥ − − w = perpW v = v projW v = 5 5 = 0 − − 1 5 2 3 3 It is clear that v = w + w⊥.
    [Show full text]
  • The Alphabets of the Bible: Latin and English John Carder
    274 The Testimony, July 2004 The alphabets of the Bible: Latin and English John Carder N A PREVIOUS article we looked at the trans- • The first major change is in the third letter, formation of the Hebrew aleph-bet into the originally the Hebrew gimal and then the IGreek alphabet (Apr. 2004, p. 130). In turn Greek gamma. The Etruscan language had no the Greek was used as a basis for writing down G sound, so they changed that place in the many other languages. Always the spoken lan- alphabet to a K sound. guage came first and writing later. We complete The Greek symbol was rotated slightly our look at the alphabets of the Bible by briefly by the Romans and then rounded, like the B considering Latin, then our English alphabet in and D symbols. It became the Latin letter C which we normally read the Bible. and, incidentally, created the confusion which still exists in English. Our C can have a hard From Greek to Latin ‘k’ sound, as in ‘cold’, or a soft sound, as in The Greek alphabet spread to the Romans from ‘city’. the Greek colonies on the coast of Italy, espe- • In the sixth place, either the Etruscans or the cially Naples and district. (Naples, ‘Napoli’ in Romans revived the old Greek symbol di- Italian, is from the Greek ‘Neapolis’, meaning gamma, which had been dropped as a letter ‘new city’). There is evidence that the Etruscans but retained as a numeral. They gave it an ‘f’ were also involved in an intermediate stage.
    [Show full text]
  • Fonts for Latin Paleography 
    FONTS FOR LATIN PALEOGRAPHY Capitalis elegans, capitalis rustica, uncialis, semiuncialis, antiqua cursiva romana, merovingia, insularis majuscula, insularis minuscula, visigothica, beneventana, carolina minuscula, gothica rotunda, gothica textura prescissa, gothica textura quadrata, gothica cursiva, gothica bastarda, humanistica. User's manual 5th edition 2 January 2017 Juan-José Marcos [email protected] Professor of Classics. Plasencia. (Cáceres). Spain. Designer of fonts for ancient scripts and linguistics ALPHABETUM Unicode font http://guindo.pntic.mec.es/jmag0042/alphabet.html PALEOGRAPHIC fonts http://guindo.pntic.mec.es/jmag0042/palefont.html TABLE OF CONTENTS CHAPTER Page Table of contents 2 Introduction 3 Epigraphy and Paleography 3 The Roman majuscule book-hand 4 Square Capitals ( capitalis elegans ) 5 Rustic Capitals ( capitalis rustica ) 8 Uncial script ( uncialis ) 10 Old Roman cursive ( antiqua cursiva romana ) 13 New Roman cursive ( nova cursiva romana ) 16 Half-uncial or Semi-uncial (semiuncialis ) 19 Post-Roman scripts or national hands 22 Germanic script ( scriptura germanica ) 23 Merovingian minuscule ( merovingia , luxoviensis minuscula ) 24 Visigothic minuscule ( visigothica ) 27 Lombardic and Beneventan scripts ( beneventana ) 30 Insular scripts 33 Insular Half-uncial or Insular majuscule ( insularis majuscula ) 33 Insular minuscule or pointed hand ( insularis minuscula ) 38 Caroline minuscule ( carolingia minuscula ) 45 Gothic script ( gothica prescissa , quadrata , rotunda , cursiva , bastarda ) 51 Humanist writing ( humanistica antiqua ) 77 Epilogue 80 Bibliography and resources in the internet 81 Price of the paleographic set of fonts 82 Paleographic fonts for Latin script 2 Juan-José Marcos: [email protected] INTRODUCTION The following pages will give you short descriptions and visual examples of Latin lettering which can be imitated through my package of "Paleographic fonts", closely based on historical models, and specifically designed to reproduce digitally the main Latin handwritings used from the 3 rd to the 15 th century.
    [Show full text]
  • (R ,T)= Ù Iux, Y,Z,T )+ Ù Jvx, Y,Z,T Ù Kwx, Y, Z,T ∂ V ∂ T ∂ V ∂ X ∂ V ∂ Y
    IV. DIFFERENTIAL RELATIONS FOR A FLUID PARTICLE This chapter presents the development and application of the basic differential equations of fluid motion. Simplifications in the general equations and common boundary conditions are presented that allow exact solutions to be obtained. Two of the most common simplifications are 1) steady flow and 2) incompressible flow. The Acceleration Field of a Fluid A general expression of the flow field velocity vector is given by V (r ,t) = iˆ u( x, y,z,t) + jˆ v(x, y,z,t) + kˆ w( x, y, z,t) One of two reference frames can be used to specify the flow field characteristics eulerian – the coordinates are fixed and we observe the flow field characteristics as it passes by the fixed coordinates. lagrangian - the coordinates move through the flow field following individual particles in the flow. Since the primary equation used in specifying the flow field velocity is based on Newton’s second law, the acceleration vector is an important solution parameter. In cartesian coordinates, this is expressed as d V ∂ V ∂ V ∂ V ∂ V ∂ V a = = + u + v + w = + ()V ⋅∇ V dt ∂ t ∂ x ∂ y ∂ z ∂ t total local convective The acceleration vector is expressed in terms of three types of derivatives: Total acceleration = total derivative of velocity vector = local derivative + convective derivative of velocity vector IV - 1 Likewise, the total derivative (also referred to as the substantial derivative ) of other variables can be expressed in a similar form, e.g. dP ∂ P ∂ P ∂ P ∂ P ∂ P = + u + v + w = + ()V ⋅∇ P dt ∂ t ∂ x ∂ y ∂ z ∂ t Example 4.1 Given the eulerian velocity-vector field 2 V = 3t iˆ + xzjˆ + ty kˆ find the acceleration of the particle.
    [Show full text]
  • Roman Numerals
    ROMAN NUMERALS Romans developed a different system of numeration about 2000 years ago Roman numerals. There are seven basic Roman numerals. These numerals and corresponding Hindu Arabic numerals are given below. Roman Numerals I V X L C D M Hindu- Arabic 1 5 10 50 100 500 1000 Numerals Writing Numbers in Roman Numerals You already know about the numerals I, V and X and the method to write numbers up to 39. Here, we will learn how to write large numbers using Roman numerals. Note! There is no symbol form in Roman system Rule 1 When a letter is used more than once, we add its value each time to get the number Examples: II= 1 + 1 = 2 XXX = 10 + 10 + 10 = 30 CCC = 100 + 100 + 100 MM = 1000 + 1000 = 2000 MMM = 1000 + 1000 + 1000 = 3000 Note! 1. The some symbol cannot be repeated more than 3 times together 2. The symbol V, L ond ore never repeated Rule 2 When a symbol of smaller value is written to the right of a symbol of larger value, add the two values. Examples: VII = 5 +1+1= 7 XXVII = 10 + 10 + 5 + 1 + 1 = 27 LXVI = 50 + 10 + 5+1 = 66 CLXV = 100 + 50 + 10 + 5 = 165 XII = 10 +1+1= 12 LVII = 50 + 5 + 1 + 1 = 57 CVII = 100 + 5 +1+1 = 107 DC = 500 + 100 = 600 MDCXVIII = 1000 + 500 + 100 + 10 + 5 +1+1 +1 = 1618 Rule 3 When a symbol of smaller value is written to the left of a symbol of larger value, the smaller value is subtracted from the larger value.
    [Show full text]