DOCSLIB.ORG

Orthogonality Inner Or Dot Product in R : Uv = U · V = U V1 +

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Orthogonality Inner Or Dot Product in R : Uv = U · V = U V1 + Math 52 0 - Linear algebra, Spring Semester 2012-2013 Dan Abramovich Orthogonality n Inner or dot product in R : T u v = u · v = u1v1 + ··· unvn examples Properties: • u · v = v · u • (u + v) · w = u · w + v · w • (cv) · w = c(v · w) • u · u ≥ 0, and u · u > 0 unless u = 0. 1 2 Norm = length: p kvk = v · v u is a unit vector if kuk = 1. If v =6 0 then 1 u = v kvk is a unit vector positively-proportional examples! to v. 3 We argue that u ? v if and only if ku − vk = ku − (−v)k. perpendicular or or- thogonal This means (u−v)·(u−v) = (u+v)·(u+v) Expand and get kuk2 + kvk2 − 2u · v = kuk2 + kvk2 + 2u · v So u ? v () u · v = 0 4 Exercise: u ? v () kuk2 + kvk2 = ku + vk2 Angles: We define the angle cosine between nonzero u and v to be cos θ = u·v examples! kuk kvk This fits with the law of cosines! 5 n W ⊂ R a subspace. we say u ? W if for all v 2 W we have u ? v: ? n W = fu 2 R ju ? W g. 6 Theorem: if fv1;:::; vkg spans W then u ? W if and only if u ? vi for all i: ? n Theorem: W ⊂ R is a subspace. Theorem: dim W + dim W ? = n Theorem: (W ?)? = W . 7 Key examples: Row (A)? = Null (A). Col (A)? = Null (AT ) 8 fu1;:::; ukg is an orthogonal set if u ? u whenever i =6 j. 3 examples - fill in R ! i j Theorem. If fu1;:::; ukg is an orthogonal set and ui are non-zero, prove it!! then they are linearly independent. 9 An orthogonal set of non-zero vec- tors is a basis for its span. Definition: An orthogonal basis of W is a basis which is an orthogo- nal set. just a change of per- spective Theorem. If fu1;:::; ukg is an orthogonal basis for W and we want to decompose a vector y 2 W as y = c1u1 + ··· + ckuk then y · ui examples!! cj = : ui · ui 10 Things get better if we normalize: fu1;:::; ukg is an orthonormal set if it is an orthogonal set of unit examples! vectors. 11 Theorem. A matrix U has or- thonormal columns if and only if UT U = I: Theorem. If U has orthonormal columns then (Ux) · (Uy) = x · y Corollary If U has orthonormal columns then •k Uxk = kxk • x ? y () Ux ? Uy 12 If U is a square matrix with or- thonormal columns then it is called an orthogonal matrix. Note: UT U = I; and U a square matrix means UUT = I: meaning the rows are also orthonor- mal! 13 Suppose fu1;:::; ukg is an orthog- onal basis for W but y 62 W . What can we do? Theorem. There is a unique expression y = yW + yW ? ? where yW 2 W and yW ? 2 W . In fact yW = c1u1 + ··· + ckuk where y · ui examples!! cj = : ui · ui 14 If fu1;:::; ukg is orthonormal, the formula gets simpler: yW = (y · u1)u1 + ··· + (y · uk)uk Writing U = [u1 ::: uk] this gives T yW = UU y 15 We call yW the perpendicular pro- jection of y on W . Notation: yW = projW y So y = projW y + projW ? y: Then yW is the vector in W closest to W . 16 Gram-Schmidt Algorithm. Say fx1;:::; xkg is a basis for W . Think about Wi = Span fx1; xig We construct inductively vi as fol- examples! lows: v1 = x1 v2 = Proj ? x2 =x2−ProjW x2 W1 1 x2 · v1 = x2 − v1 v1 · v1 . vk = Proj ? xk Wk−1 xk·v1 xk·vk−1 = x − v1+···+ v k v1·v1 vk−1·vk−1 k−1 1 We can normalize: ui = vi. kvik 17 QR factorization Matrix interpretation of Gram-Schmidt: say A has linearly independent columns A = [x1 ··· xn] and say Q = [u1 ··· un]: Since Span (u1;:::; ui) = Span (x1;:::; xi) we have xi = r1iu1 + ··· + riiui 2 3 r1i 6 . 7 6 . 7 6 7 6rii7 meaning xi = Q6 7 6 0 7 6 . 7 4 . 5 0 So A = [x1 ··· xn] = Q[r1 ··· rn]. 18 In other words A = QR, where Q has orthonormal columns, and R is invertible upper triangular. Note: R = QT A 19 Least squares approximation. Say Col A does not span b. You still want to approximate Ax ≈ b: We'll calculate x^ such that kAx^ − bk is minimized. Then we'll apply. 20 The closest an element Ax^ of the Gram-Schmidt? column space gets to b is ouch!! ^ b = projCol A b: Now b^ 2 Col A, so we can solve Ax^ = b^: This seems hard. But. 21 ^ Ax^ = b = projCol A b: () (b − b^) ? Col A = Row AT () AT (b − Ax^) = 0 () AT A x^ = AT b 22 Linear regression Theoretically a system behaves like y = β0 + β1x; and you want to find βi. You run experiments which give data points (xi; yi). They will not actu- ally lie of a line. You get the approximate equations β0 + x1β1 ≈ y1 β0 + x2β1 ≈ y2 . β0 + xnβn ≈ yn 23 In matrix notation: 2 3 1 x1 2 3 y1 61 x27 β1 . 6. 7 ≈ 4 . 5 4. 5 β2 yn 1 xn or Xβ ≈ y: 24 To solve it we take XT Xβ = XT y We can solve directly, or expand: P P n xi β0 yi P P 2 = P xi xi β1 xiyi.
Load more

Recommended publications
  • Research Brief March 2017 Publication #2017-16
    Research Brief March 2017 Publication #2017-16 Flourishing From the Start: What Is It and How Can It Be Measured? Kristin Anderson Moore, PhD, Child Trends Christina D. Bethell, PhD, The Child and Adolescent Health Measurement Introduction Initiative, Johns Hopkins Bloomberg School of Every parent wants their child to flourish, and every community wants its Public Health children to thrive. It is not sufficient for children to avoid negative outcomes. Rather, from their earliest years, we should foster positive outcomes for David Murphey, PhD, children. Substantial evidence indicates that early investments to foster positive child development can reap large and lasting gains.1 But in order to Child Trends implement and sustain policies and programs that help children flourish, we need to accurately define, measure, and then monitor, “flourishing.”a Miranda Carver Martin, BA, Child Trends By comparing the available child development research literature with the data currently being collected by health researchers and other practitioners, Martha Beltz, BA, we have identified important gaps in our definition of flourishing.2 In formerly of Child Trends particular, the field lacks a set of brief, robust, and culturally sensitive measures of “thriving” constructs critical for young children.3 This is also true for measures of the promotive and protective factors that contribute to thriving. Even when measures do exist, there are serious concerns regarding their validity and utility. We instead recommend these high-priority measures of flourishing
    [Show full text]
  • Relativistic Dynamics
    Chapter 4 Relativistic dynamics We have seen in the previous lectures that our relativity postulates suggest that the most efficient (lazy but smart) approach to relativistic physics is in terms of 4-vectors, and that velocities never exceed c in magnitude. In this chapter we will see how this 4-vector approach works for dynamics, i.e., for the interplay between motion and forces. A particle subject to forces will undergo non-inertial motion. According to Newton, there is a simple (3-vector) relation between force and acceleration, f~ = m~a; (4.0.1) where acceleration is the second time derivative of position, d~v d2~x ~a = = : (4.0.2) dt dt2 There is just one problem with these relations | they are wrong! Newtonian dynamics is a good approximation when velocities are very small compared to c, but outside of this regime the relation (4.0.1) is simply incorrect. In particular, these relations are inconsistent with our relativity postu- lates. To see this, it is sufficient to note that Newton's equations (4.0.1) and (4.0.2) predict that a particle subject to a constant force (and initially at rest) will acquire a velocity which can become arbitrarily large, Z t ~ d~v 0 f ~v(t) = 0 dt = t ! 1 as t ! 1 . (4.0.3) 0 dt m This flatly contradicts the prediction of special relativity (and causality) that no signal can propagate faster than c. Our task is to understand how to formulate the dynamics of non-inertial particles in a manner which is consistent with our relativity postulates (and then verify that it matches observation, including in the non-relativistic regime).
    [Show full text]
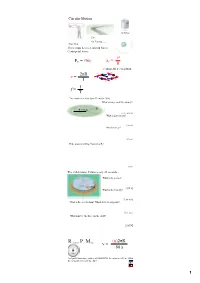
  • FC = Mac V2 R V = 2Πr T F = T 1
    Circular Motion Gravitron Cars Car Turning (has a curse) Rope Skip There must be a net inward force: Centripetal Force v2 F = maC a = C C R Centripetal acceleration 2πR v v v = R v T v 1 f = T The motorcycle rider does 13 laps in 150 s. What is his period? Frequency? R = 30 m [11.5 s, 0.087 Hz] What is his velocity? [16.3 m/s] What is his aC? [8.9 m/s2] If the mass is 180 kg, what is his FC? [1600 N] The child rotates 5 times every 22 seconds... What is the period? 60 kg [4.4 s] What is the velocity? [2.86 m/s] What is the acceleration? Which way does it point? [4.1 m/s2] What must be the force on the child? [245 N] Revolutions Per Minute (n)2πR v = 60 s An Ipod's hard drive rotates at 4200 RPM. Its radius is 0.03 m. What is the velocity in m/s of its edge? 1 Airplane Turning v = 232 m/s (520 mph) aC = 7 g's What is the turn radius? [785 m = 2757 ft] 2 FC Solving Circular Motion Problems 1. Determine FC (FBD) 2 2. Set FC = m v R 3. Solve for unknowns The book's mass is 2 kg it is spun so that the tension is 45 N. What is the velocity of the book in m/s? In RPM? R = 0.75 m [4.11 m/s] [52 RPM] What is the period (T) of the book? [1.15 s] The car is traveling at 25 m/s and the turn's radius is 63 m.
    [Show full text]
  • More on Vectors Math 122 Calculus III D Joyce, Fall 2012
    More on Vectors Math 122 Calculus III D Joyce, Fall 2012 Unit vectors. A unit vector is a vector whose length is 1. If a unit vector u in the plane R2 is placed in standard position with its tail at the origin, then it's head will land on the unit circle x2 + y2 = 1. Every point on the unit circle (x; y) is of the form (cos θ; sin θ) where θ is the angle measured from the positive x-axis in the counterclockwise direction. u=(x;y)=(cos θ; sin θ) 7 '$θ q &% Thus, every unit vector in the plane is of the form u = (cos θ; sin θ). We can interpret unit vectors as being directions, and we can use them in place of angles since they carry the same information as an angle. In three dimensions, we also use unit vectors and they will still signify directions. Unit 3 vectors in R correspond to points on the sphere because if u = (u1; u2; u3) is a unit vector, 2 2 2 3 then u1 + u2 + u3 = 1. Each unit vector in R carries more information than just one angle since, if you want to name a point on a sphere, you need to give two angles, longitude and latitude. Now that we have unit vectors, we can treat every vector v as a length and a direction. The length of v is kvk, of course. And its direction is the unit vector u in the same direction which can be found by v u = : kvk The vector v can be reconstituted from its length and direction by multiplying v = kvk u.
    [Show full text]
  • Lecture 3.Pdf
    ENGR-1100 Introduction to Engineering Analysis Lecture 3 POSITION VECTORS & FORCE VECTORS Today’s Objectives: Students will be able to : a) Represent a position vector in Cartesian coordinate form, from given geometry. In-Class Activities: • Applications / b) Represent a force vector directed along Relevance a line. • Write Position Vectors • Write a Force Vector along a line 1 DOT PRODUCT Today’s Objective: Students will be able to use the vector dot product to: a) determine an angle between In-Class Activities: two vectors, and, •Applications / Relevance b) determine the projection of a vector • Dot product - Definition along a specified line. • Angle Determination • Determining the Projection APPLICATIONS This ship’s mooring line, connected to the bow, can be represented as a Cartesian vector. What are the forces in the mooring line and how do we find their directions? Why would we want to know these things? 2 APPLICATIONS (continued) This awning is held up by three chains. What are the forces in the chains and how do we find their directions? Why would we want to know these things? POSITION VECTOR A position vector is defined as a fixed vector that locates a point in space relative to another point. Consider two points, A and B, in 3-D space. Let their coordinates be (XA, YA, ZA) and (XB, YB, ZB), respectively. 3 POSITION VECTOR The position vector directed from A to B, rAB , is defined as rAB = {( XB –XA ) i + ( YB –YA ) j + ( ZB –ZA ) k }m Please note that B is the ending point and A is the starting point.
    [Show full text]
  • Teresa Blackford V. Welborn Clinic
    IN THE Indiana Supreme Court Supreme Court Case No. 21S-CT-85 Teresa Blackford Appellant (Plaintiff below) –v– Welborn Clinic Appellee (Defendant below) Argued: April 22, 2021 | Decided: August 31, 2021 Appeal from the Vanderburgh Circuit Court No. 82C01-1804-CT-2434 The Honorable David D. Kiely, Judge On Petition to Transfer from the Indiana Court of Appeals No. 19A-CT-2054 Opinion by Justice Goff Chief Justice Rush and Justices David, Massa, and Slaughter concur. Goff, Justice. Statutory limitations of action are “fundamental to a well-ordered judicial system.” See Bd. of Regents of Univ. of State of N. Y. v. Tomanio, 446 U.S. 478, 487 (1980). The process of discovery and trial, revealing ultimate facts that either help or harm the plaintiff, are “obviously more reliable if the witness or testimony in question is relatively fresh.” Id. And potential defendants, of course, seek to avoid indefinite liability for past conduct. C. Corman, 1 Limitation of Actions § 1.1, at 5 (1991). Naturally, then, “there comes a point at which the delay of a plaintiff in asserting a claim is sufficiently likely either to impair the accuracy of the fact-finding process or to upset settled expectations that a substantive claim will be barred” regardless of its merit. Tomanio, 446 U.S. at 487. At the same time, most courts recognize that certain circumstances may “justify an exception to these strong policies of repose,” extending the time in which a plaintiff may file a claim—a process known as “tolling.” Id. at 487–88. The circumstances here present us with these competing interests: the plaintiff, having been misinformed of a medical diagnosis by her provider, which dissolved its business more than five years prior to the plaintiff filing her complaint, seeks relief for her injuries on grounds of fraudulent concealment, despite expiration of the applicable limitation period.
    [Show full text]
  • Chapter 3 Motion in Two and Three Dimensions
    Chapter 3 Motion in Two and Three Dimensions 3.1 The Important Stuff 3.1.1 Position In three dimensions, the location of a particle is specified by its location vector, r: r = xi + yj + zk (3.1) If during a time interval ∆t the position vector of the particle changes from r1 to r2, the displacement ∆r for that time interval is ∆r = r1 − r2 (3.2) = (x2 − x1)i +(y2 − y1)j +(z2 − z1)k (3.3) 3.1.2 Velocity If a particle moves through a displacement ∆r in a time interval ∆t then its average velocity for that interval is ∆r ∆x ∆y ∆z v = = i + j + k (3.4) ∆t ∆t ∆t ∆t As before, a more interesting quantity is the instantaneous velocity v, which is the limit of the average velocity when we shrink the time interval ∆t to zero. It is the time derivative of the position vector r: dr v = (3.5) dt d = (xi + yj + zk) (3.6) dt dx dy dz = i + j + k (3.7) dt dt dt can be written: v = vxi + vyj + vzk (3.8) 51 52 CHAPTER 3. MOTION IN TWO AND THREE DIMENSIONS where dx dy dz v = v = v = (3.9) x dt y dt z dt The instantaneous velocity v of a particle is always tangent to the path of the particle. 3.1.3 Acceleration If a particle’s velocity changes by ∆v in a time period ∆t, the average acceleration a for that period is ∆v ∆v ∆v ∆v a = = x i + y j + z k (3.10) ∆t ∆t ∆t ∆t but a much more interesting quantity is the result of shrinking the period ∆t to zero, which gives us the instantaneous acceleration, a.
    [Show full text]
  • Linear Functions. Definition. Suppose V and W Are Vector Spaces and L
    Linear functions. Definition. Suppose V and W are vector spaces and L : V → W. (Remember: This means that L is a function; the domain of L equals V ; and the range of L is a subset of W .) We say L is linear if L(cv) = cL(v) whenever c ∈ R and v ∈ V and L(v1 + v2) = L(v1) + L(v2) whenever v1, v2 ∈ V . We let ker L = {v ∈ V : L(v) = 0} and call ker L the kernel of L and we let rng L = {L(v): v ∈ V } so rng L is the range of L. We let L(V, W ) be the set of L such that L : V → W and L is linear. Example. Suppose m and n are positive integers and L ∈ L(Rn, Rm). For each i = 1, . , m and each j = 1, . , n we let i lj be the i-th component of L(ej). Thus Xm 1 m i L(ej) = (lj , . , lj ) = ljei whenever j = 1, . , n. i=1 n Suppose x = (x1, . , xn) ∈ R . Then Xn x = xjej j=1 so à ! 0 1 Xn Xn Xn Xn Xm Xm Xn i @ i A L(x) = L( xjej) = L(xjej) = xjL(ej) = xj ljei = xjlj ei. j=1 j=1 j=1 j=1 i=1 i=1 j=1 We call 2 1 1 1 3 l1 l2 ··· ln 6 7 6 2 1 2 7 6 l1 22 ··· ln 7 6 7 6 . .. 7 4 . 5 m m m l1 l2 ··· ln the standard matrix of L.
    [Show full text]
  • Concept of a Dyad and Dyadic: Consider Two Vectors a and B Dyad: It Consists of a Pair of Vectors a B for Two Vectors a a N D B
    1/11/2010 CHAPTER 1 Introductory Concepts • Elements of Vector Analysis • Newton’s Laws • Units • The basis of Newtonian Mechanics • D’Alembert’s Principle 1 Science of Mechanics: It is concerned with the motion of material bodies. • Bodies have different scales: Microscropic, macroscopic and astronomic scales. In mechanics - mostly macroscopic bodies are considered. • Speed of motion - serves as another important variable - small and high (approaching speed of light). 2 1 1/11/2010 • In Newtonian mechanics - study motion of bodies much bigger than particles at atomic scale, and moving at relative motions (speeds) much smaller than the speed of light. • Two general approaches: – Vectorial dynamics: uses Newton’s laws to write the equations of motion of a system, motion is described in physical coordinates and their derivatives; – Analytical dynamics: uses energy like quantities to define the equations of motion, uses the generalized coordinates to describe motion. 3 1.1 Vector Analysis: • Scalars, vectors, tensors: – Scalar: It is a quantity expressible by a single real number. Examples include: mass, time, temperature, energy, etc. – Vector: It is a quantity which needs both direction and magnitude for complete specification. – Actually (mathematically), it must also have certain transformation properties. 4 2 1/11/2010 These properties are: vector magnitude remains unchanged under rotation of axes. ex: force, moment of a force, velocity, acceleration, etc. – geometrically, vectors are shown or depicted as directed line segments of proper magnitude and direction. 5 e (unit vector) A A = A e – if we use a coordinate system, we define a basis set (iˆ , ˆj , k ˆ ): we can write A = Axi + Ay j + Azk Z or, we can also use the A three components and Y define X T {A}={Ax,Ay,Az} 6 3 1/11/2010 – The three components Ax , Ay , Az can be used as 3-dimensional vector elements to specify the vector.
    [Show full text]
  • Two Worked out Examples of Rotations Using Quaternions
    TWO WORKED OUT EXAMPLES OF ROTATIONS USING QUATERNIONS This note is an attachment to the article \Rotations and Quaternions" which in turn is a companion to the video of the talk by the same title. Example 1. Determine the image of the point (1; −1; 2) under the rotation by an angle of 60◦ about an axis in the yz-plane that is inclined at an angle of 60◦ to the positive y-axis. p ◦ ◦ 1 3 Solution: The unit vector u in the direction of the axis of rotation is cos 60 j + sin 60 k = 2 j + 2 k. The quaternion (or vector) corresponding to the point p = (1; −1; 2) is of course p = i − j + 2k. To find −1 θ θ the image of p under the rotation, we calculate qpq where q is the quaternion cos 2 + sin 2 u and θ the angle of rotation (60◦ in this case). The resulting quaternion|if we did the calculation right|would have no constant term and therefore we can interpret it as a vector. That vector gives us the answer. p p p p p We have q = 3 + 1 u = 3 + 1 j + 3 k = 1 (2 3 + j + 3k). Since q is by construction a unit quaternion, 2 2 2 4 p4 4 p −1 1 its inverse is its conjugate: q = 4 (2 3 − j − 3k). Now, computing qp in the routine way, we get 1 p p p p qp = ((1 − 2 3) + (2 + 3 3)i − 3j + (4 3 − 1)k) 4 and then another long but routine computation gives 1 p p p qpq−1 = ((10 + 4 3)i + (1 + 2 3)j + (14 − 3 3)k) 8 The point corresponding to the vector on the right hand side in the above equation is the image of (1; −1; 2) under the given rotation.
    [Show full text]
  • 1. Roman Numerals
    Chapter 1: Roman Numerals 1. Roman Numerals Introduction: In ancient Europe, people used some capital Roman letters to write numbers. Hence these numerals were known as Roman numerals. In this chapter, we will learn to write Roman numerals from 1 to 20. We see the use of Roman numerals in several clocks and watches, ancient European coins, books etc. Summative Assessment Let’s Study Symbols used for writing Roman numerals The three basic symbols used to write Roman numerals are given in the table below: Symbol used as Roman numeral I V X Numeric value represented by it 1 5 10 [Note: (1) There is no symbol for zero in Roman numerals. (2) The value of a symbol used for Roman numeral does not change with its place.] Rules for writing Roman numerals The rules for writing numbers from 1 to 20 using the Roman numerals are as follows: Rule 1: The number formed by writing the symbols I or X consecutively two or three times is the sum of the numeric values of the individual symbols. Examples: II = 1 + 1 = 2, III = 1 + 1 + 1 = 3, XX = 10 + 10 = 20 1 Std. V: Mathematics Rule 2: The consecutive repetition of symbols I and X is allowed for a maximum of three times to form a number. However, the symbol V is never repeated. Examples: (1) III = 3, however IIII ≠ 4 (2) XXX = 30, however XXXX ≠ 40 (3) VV ≠ 10 and VVV ≠ 15. Rule 3: When either I or V is written on the right side of the symbol of a bigger number, add its value to the value of the bigger number.
    [Show full text]
  • Proposal for Generation Panel for Latin Script Label Generation Ruleset for the Root Zone
    Generation Panel for Latin Script Label Generation Ruleset for the Root Zone Proposal for Generation Panel for Latin Script Label Generation Ruleset for the Root Zone Table of Contents 1. General Information 2 1.1 Use of Latin Script characters in domain names 3 1.2 Target Script for the Proposed Generation Panel 4 1.2.1 Diacritics 5 1.3 Countries with significant user communities using Latin script 6 2. Proposed Initial Composition of the Panel and Relationship with Past Work or Working Groups 7 3. Work Plan 13 3.1 Suggested Timeline with Significant Milestones 13 3.2 Sources for funding travel and logistics 16 3.3 Need for ICANN provided advisors 17 4. References 17 1 Generation Panel for Latin Script Label Generation Ruleset for the Root Zone 1. General Information The Latin script1 or Roman script is a major writing system of the world today, and the most widely used in terms of number of languages and number of speakers, with circa 70% of the world’s readers and writers making use of this script2 (Wikipedia). Historically, it is derived from the Greek alphabet, as is the Cyrillic script. The Greek alphabet is in turn derived from the Phoenician alphabet which dates to the mid-11th century BC and is itself based on older scripts. This explains why Latin, Cyrillic and Greek share some letters, which may become relevant to the ruleset in the form of cross-script variants. The Latin alphabet itself originated in Italy in the 7th Century BC. The original alphabet contained 21 upper case only letters: A, B, C, D, E, F, Z, H, I, K, L, M, N, O, P, Q, R, S, T, V and X.
    [Show full text]