Molecular Classification of Cancer: Unsupervised Self- Organizing Map Analysis of Gene Expression Microarray Data1
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-
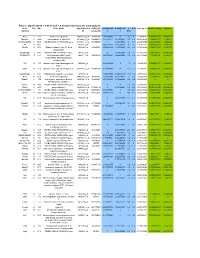
Table 2. Significant
Table 2. Significant (Q < 0.05 and |d | > 0.5) transcripts from the meta-analysis Gene Chr Mb Gene Name Affy ProbeSet cDNA_IDs d HAP/LAP d HAP/LAP d d IS Average d Ztest P values Q-value Symbol ID (study #5) 1 2 STS B2m 2 122 beta-2 microglobulin 1452428_a_at AI848245 1.75334941 4 3.2 4 3.2316485 1.07398E-09 5.69E-08 Man2b1 8 84.4 mannosidase 2, alpha B1 1416340_a_at H4049B01 3.75722111 3.87309653 2.1 1.6 2.84852656 5.32443E-07 1.58E-05 1110032A03Rik 9 50.9 RIKEN cDNA 1110032A03 gene 1417211_a_at H4035E05 4 1.66015788 4 1.7 2.82772795 2.94266E-05 0.000527 NA 9 48.5 --- 1456111_at 3.43701477 1.85785922 4 2 2.8237185 9.97969E-08 3.48E-06 Scn4b 9 45.3 Sodium channel, type IV, beta 1434008_at AI844796 3.79536664 1.63774235 3.3 2.3 2.75319499 1.48057E-08 6.21E-07 polypeptide Gadd45gip1 8 84.1 RIKEN cDNA 2310040G17 gene 1417619_at 4 3.38875643 1.4 2 2.69163229 8.84279E-06 0.0001904 BC056474 15 12.1 Mus musculus cDNA clone 1424117_at H3030A06 3.95752801 2.42838452 1.9 2.2 2.62132809 1.3344E-08 5.66E-07 MGC:67360 IMAGE:6823629, complete cds NA 4 153 guanine nucleotide binding protein, 1454696_at -3.46081884 -4 -1.3 -1.6 -2.6026947 8.58458E-05 0.0012617 beta 1 Gnb1 4 153 guanine nucleotide binding protein, 1417432_a_at H3094D02 -3.13334396 -4 -1.6 -1.7 -2.5946297 1.04542E-05 0.0002202 beta 1 Gadd45gip1 8 84.1 RAD23a homolog (S. -

Erk Direction of CD4 T Cell Subsets Chiung-Fang Chang, Warren N
Polar Opposites: Erk Direction of CD4 T Cell Subsets Chiung-Fang Chang, Warren N. D'Souza, Irene L. Ch'en, Gilles Pages, Jacques Pouyssegur and Stephen M. Hedrick This information is current as of September 25, 2021. J Immunol 2012; 189:721-731; Prepublished online 6 June 2012; doi: 10.4049/jimmunol.1103015 http://www.jimmunol.org/content/189/2/721 Downloaded from Supplementary http://www.jimmunol.org/content/suppl/2012/06/06/jimmunol.110301 Material 5.DC1 References This article cites 67 articles, 28 of which you can access for free at: http://www.jimmunol.org/ http://www.jimmunol.org/content/189/2/721.full#ref-list-1 Why The JI? Submit online. • Rapid Reviews! 30 days* from submission to initial decision • No Triage! Every submission reviewed by practicing scientists by guest on September 25, 2021 • Fast Publication! 4 weeks from acceptance to publication *average Subscription Information about subscribing to The Journal of Immunology is online at: http://jimmunol.org/subscription Permissions Submit copyright permission requests at: http://www.aai.org/About/Publications/JI/copyright.html Email Alerts Receive free email-alerts when new articles cite this article. Sign up at: http://jimmunol.org/alerts The Journal of Immunology is published twice each month by The American Association of Immunologists, Inc., 1451 Rockville Pike, Suite 650, Rockville, MD 20852 Copyright © 2012 by The American Association of Immunologists, Inc. All rights reserved. Print ISSN: 0022-1767 Online ISSN: 1550-6606. The Journal of Immunology Polar Opposites: Erk Direction of CD4 T Cell Subsets Chiung-Fang Chang,* Warren N. D’Souza,† Irene L. -

Atbf1 Is Required for the Pit1 Gene Early Activation
Atbf1 is required for the Pit1 gene early activation Yingchuan Qi*, Jeffrey A. Ranish†, Xiaoyan Zhu*, Anna Krones*, Jie Zhang*, Ruedi Aebersold†‡, David W. Rose§, Michael G. Rosenfeld*¶, and Catherine Carrie` re¶ʈ *Howard Hughes Medical Institute and Department of Medicine, School of Medicine, University of California at San Diego, La Jolla, CA 92093; †Institute for Systems Biology, 1441 North 34th Street, Seattle, WA 98103; ‡Institute of Molecular Systems Biology, Swiss Federal Institute of Technology (ETH) Ho¨nggerberg and Faculty of Sciences, University of Zu¨rich, CH-8093 Zu¨rich, Switzerland; §Department of Medicine, Division of Endocrinology and Metabolism, School of Medicine, University of California at San Diego, La Jolla, CA 92093; and ʈDepartment of Medicine, Dartmouth Medical School, Norris Cotton Cancer Center, 1 Medical Center Drive, Lebanon, NH 03756 Contributed by Michael G. Rosenfeld, December 24, 2007 (sent for review November 28, 2007) Enhancers have been functionally described for >35 years, but the Pit1-defective Snell (dw/dw) mutant mice, demonstrating that the molecular principles underlying the integration of regulatory in- elements required for Pit1 early activation were present in the same puts to alternate gene enhancers used during mammalian orga- genomic region (10). Further mapping showed that the regions nogenesis remain incompletely understood. Using a combination required for the Pit1 early activation were located between Ϫ10 kb of in vivo enhancer mapping and proteomics approaches, we have and Ϫ3.5 kb (10). Thus, Pit1 expression appears to be under the established that two distant and distinct early enhancers, each control of multiple enhancers, at least one for its activation and one requiring different transcription complexes, are required for full for its maintained expression. -

Gene Expression Profile of Amyloid Beta Protein-Injected Mouse Model for Alzheimer Disease
Acta Pharmacologica Sinica 2005 Jun; 26 (6): 666–672 Full-length article Gene expression profile of amyloid beta protein-injected mouse model for Alzheimer disease Ling-na KONG, Ping-ping ZUO1, Liang MU, Yan-yong LIU, Nan YANG Department of Pharmacology, School of Basic Medicine, Peking Union Medical College and Chinese Academy of Medical Sciences, Beijing 100005, China Key words Abstract Alzheimer disease; dementia; amyloid beta- Aim: To investigate the gene expression profile changes in the cerebral cortex of protein; cDNA microarray mice injected icv with amyloid beta-protein (Aβ) fragment 25-35 using cDNA microarray. Methods: Balb/c mice were randomly divided into a control group and 1 Correspondence to Prof Ping-ping ZUO. Aβ-treated group. The Morris water maze test was performed to detect the effect Phn/Fax 86-10-6529-6404. of Aβ-injection on the learning and memory of mice. Atlas Mouse 1.2 Expression E-mail [email protected] Arrays containing 1176 genes were used to investigate the gene expression pat- Received 2004-11-25 tern of each group. Results: The gene expression profiles showed that 19 genes Accepted 2005-03-14 including TBX1, NF-κB, AP-1/c-Jun, cadherin, integrin, erb-B2, and FGFR1 were doi: 10.1111/j.1745-7254.2005.00129.x up-regulated after 2 weeks of icv administration of Aβ; while 12 genes were down- regulated, including NGF, glucose phosphate isomerase 1, AT motif binding fac- tor 1, Na+/K+-ATPase, and Akt. Conclusions: The results provide important leads for pursuing a more complete understanding of the molecular events of Aβ- injection into mice with Alzheimer disease. -

Regulation of Skeletal Muscle Differentiation by ATBF1, a Multiple Homeodomain-Zinc Finger Transcription Factor
University of Calgary PRISM: University of Calgary's Digital Repository Graduate Studies Legacy Theses 2000 Regulation of skeletal muscle differentiation by ATBF1, a multiple homeodomain-zinc finger transcription factor Berry, Fred Brandon Berry, F. B. (2000). Regulation of skeletal muscle differentiation by ATBF1, a multiple homeodomain-zinc finger transcription factor (Unpublished doctoral thesis). University of Calgary, Calgary, AB. doi:10.11575/PRISM/23689 http://hdl.handle.net/1880/39899 doctoral thesis University of Calgary graduate students retain copyright ownership and moral rights for their thesis. You may use this material in any way that is permitted by the Copyright Act or through licensing that has been assigned to the document. For uses that are not allowable under copyright legislation or licensing, you are required to seek permission. Downloaded from PRISM: https://prism.ucalgary.ca NOTE TO USERS Page(s) not included in the original manuscript and are unavailable from the author or university. The manuscript was microfilmed as received. This reproduction is the best copy available. THE UNIVERSITY OF CALGARY Regulation of Skeletal MuscIe Differentiation by ATBF1, a Multiple Homeodomain-zinc Finger Transcription Factor Fred Brandon Berry A DISSERTATION SUBMITTED TO THlE FACC?TYOF GRADUATE STUDIES IN PARTIAL FULFILMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY DEPARTMENT OF BIOCHEMISTRY AND MOLECULAR BIOLOGY CALGARY, ALBERTA APRIL, 2000 O Fred Brandon Berry 2000 National Library Bibliotheque nationale I+IofCanada -

Regulating the Suprachiasmatic Nucleus (SCN) Circadian Clockwork: Interplay Between Cell- Autonomous and Circuit-Level Mechanisms
Downloaded from http://cshperspectives.cshlp.org/ on October 8, 2021 - Published by Cold Spring Harbor Laboratory Press Regulating the Suprachiasmatic Nucleus (SCN) Circadian Clockwork: Interplay between Cell- Autonomous and Circuit-Level Mechanisms Erik D. Herzog,1 Tracey Hermanstyne,1 Nicola J. Smyllie,2 and Michael H. Hastings2 1Department of Biology, Washington University in St. Louis, St. Louis, Missouri 63130-4899 2Division of Neurobiology, MRC Laboratory of Molecular Biology, Cambridge CB2 0QH, United Kingdom Correspondence: [email protected]; [email protected] The suprachiasmatic nucleus (SCN) is the principal circadian clock of the brain, directing daily cycles of behavior and physiology. SCN neurons contain a cell-autonomous transcrip- tion-based clockwork but, in turn, circuit-level interactions synchronize the 20,000 or so SCN neurons into a robust and coherent daily timer. Synchronization requires neuropeptide signaling, regulated by a reciprocal interdependence between the molecular clockwork and rhythmic electrical activity, which in turn depends on a daytime Naþ drive and nighttime Kþ drag. Recent studies exploiting intersectional genetics have started to identify the pacemak- ing roles of particular neuronal groups in the SCN. They support the idea that timekeeping involves nonlinear and hierarchical computations that create and incorporate timing infor- mation through the interactions between key groups of neurons within the SCN circuit. The field is now poised to elucidate these computations, their underlying cellular mechanisms, and how the SCN clock interacts with subordinate circadian clocks across the brain to determine the timing and efficiency of the sleep–wake cycle, and how perturbations of this coherence contribute to neurological and psychiatric illness. -

Spatial and Temporal Patterns of Gene Expression During Neurogenesis in the Sea Urchin Lytechinus Variegatus Leslie A
Slota et al. EvoDevo (2019) 10:2 https://doi.org/10.1186/s13227-019-0115-8 EvoDevo RESEARCH Open Access Spatial and temporal patterns of gene expression during neurogenesis in the sea urchin Lytechinus variegatus Leslie A. Slota , Esther M. Miranda and David R. McClay* Abstract Background: The sea urchin is a basal deuterostome that is more closely related to vertebrates than many organisms traditionally used to study neurogenesis. This phylogenetic position means that the sea urchin can provide insights into the evolution of the nervous system by helping resolve which developmental processes are deuterostome inno- vations, which are innovations in other clades, and which are ancestral. However, the nervous system of echinoderms is one of the least understood of all major metazoan phyla. To gain insights into echinoderm neurogenesis, spatial and temporal gene expression data are essential. Then, functional data will enable the building of a detailed gene regula- tory network for neurogenesis in the sea urchin that can be compared across metazoans to resolve questions about how nervous systems evolved. Results: Here, we analyze spatiotemporal gene expression during sea urchin neurogenesis for genes that have been shown to be neurogenic in one or more species. We report the expression of 21 genes expressed in areas of neurogenesis in the sea urchin embryo from blastula stage (just before neural progenitors begin their specifca- tion sequence) through pluteus larval stage (when much of the nervous system has been patterned). Among those 21 gene expression patterns, we report expression of 11 transcription factors and 2 axon guidance genes, each expressed in discrete domains in the neuroectoderm or in the endoderm. -

Genome-Wide Analysis of the Mouse Lung Transcriptome Reveals
Alberts et al. Respiratory Research 2011, 12:61 http://respiratory-research.com/content/12/1/61 RESEARCH Open Access Genome-wide analysis of the mouse lung transcriptome reveals novel molecular gene interaction networks and cell-specific expression signatures Rudi Alberts1,LuLu2,3, Robert W Williams2 and Klaus Schughart1* Abstract Background: The lung is critical in surveillance and initial defense against pathogens. In humans, as in mice, individual genetic differences strongly modulate pulmonary responses to infectious agents, severity of lung disease, and potential allergic reactions. In a first step towards understanding genetic predisposition and pulmonary molecular networks that underlie individual differences in disease vulnerability, we performed a global analysis of normative lung gene expression levels in inbred mouse strains and a large family of BXD strains that are widely used for systems genetics. Our goal is to provide a key community resource on the genetics of the normative lung transcriptome that can serve as a foundation for experimental analysis and allow predicting genetic predisposition and response to pathogens, allergens, and xenobiotics. Methods: Steady-state polyA+ mRNA levels were assayed across a diverse and fully genotyped panel of 57 isogenic strains using the Affymetrix M430 2.0 array. Correlations of expression levels between genes were determined. Global expression QTL (eQTL) analysis and network covariance analysis was performed using tools and resources in GeneNetwork http://www.genenetwork.org. Results: Expression values were highly variable across strains and in many cases exhibited a high heri-tability factor. Several genes which showed a restricted expression to lung tissue were identified. Using correlations between gene expression values across all strains, we defined and extended memberships of several important molecular networks in the lung. -

(12) Patent Application Publication (10) Pub. No.: US 2012/0322864 A1 Rossi Et Al
US 2012O322864A1 (19) United States (12) Patent Application Publication (10) Pub. No.: US 2012/0322864 A1 Rossi et al. (43) Pub. Date: Dec. 20, 2012 (54) SUSTAINED POLYPEPTIDE EXPRESSION (60) Provisional application No. 61/325,003, filed on Apr. FROM SYNTHETIC, MODIFIED RNAS AND 16, 2010, provisional application No. 61/387,220, USES THEREOF filed on Sep. 28, 2010. Publication Classification (75) Inventors: Derrick Rossi, Roslindale, MA (US); (51) Int. Cl. Luigi Warren, Cambridge, MA (US) CI2N5/07 (2010.01) A6IR 48/00 (2006.01) (73) Assignee: IMMUNE DISEASE INSTITUTE, C7H 2L/02 (2006.01) INC., Boston, MA (US) (52) U.S. Cl. ...................... 514/44 R; 536/23.5; 435/377 (57) ABSTRACT (21) Appl. No.: 13/590,880 Described herein are synthetic, modified RNAs for changing the phenotype of a cell. Such as expressing a polypeptide or altering the developmental potential. Accordingly, provided (22) Filed: Aug. 21, 2012 herein are compositions, methods, and kits comprising Syn thetic, modified RNAs for changing the phenotype of a cellor Related U.S. Application Data cells. These methods, compositions, and kits comprising Syn thetic, modified RNAs can be used either to express a desired (63) Continuation of application No. 13/088,009, filed on protein in a cell or tissue, or to change the differentiated Apr. 15, 2011. phenotype of a cell to that of another, desired cell type. Patent Application Publication Dec. 20, 2012 Sheet 1 of 45 US 2012/0322864 A1 s se xxx S s s nnnn s e sit. occa S. s Ra w s e s S. iiii is is iiiiSE SEE SS Patent Application Publication Dec. -

1 Table 1S. Genes Over-Expressed in AILT Vs. Normal T-Lymphocytes
Table 1S. Genes over-expressed in AILT vs. normal T-lymphocytes (corresponding to CD4+, CD8+ and HLA-DR+ elements) Over-expression (Z Gene Common GeneBank Description score) 9.38 232544_at AU144916 CDNA FLJ11572 fis, clone HEMBA1003373 9.179 220423_at PLA2G2D NM_012400 phospholipase A2, group IID 9.093 211719_x_at FN1 BC005858 fibronectin 1 9.005 204163_at EMILIN1 NM_007046 elastin microfibril interfacer 1 8.642 216442_x_at FN1 AK026737 fibronectin 1 8.552 220690_s_at DKFZp566O084 NM_015510 DKFZP566O084 protein 8.204 210072_at CCL19 U88321 chemokine (CC motif) ligand 19 7.996 230047_at FLJ32810 BF439533 nab67d10.x1 Soares_NSF_F8_9W_OT_PA_P_S1 Homo sapiens cDNA clone IMAGE:3272875 3', mRNA sequence. 7.641 225575_at LIFR AI680541 leukemia inhibitory factor receptor 7.59 215076_s_at COL3A1 AU144167 collagen, type III, alpha 1 (EhlersDanlos syndrome type IV, autosomal dominant) 7.581 204570_at COX7A1 NM_001864 cytochrome c oxidase subunit VIIa polypeptide 1 (muscle) 7.56 217767_at C3 NM_000064 complement component 3 7.411 211981_at COL4A1 NM_001845 collagen, type IV, alpha 1 7.384 204606_at CCL21 NM_002989 chemokine (CC motif) ligand 21 7.384 201162_at IGFBP7 NM_001553 insulinlike growth factor binding protein 7 7.2 208747_s_at C1S M18767 complement component 1, s subcomponent 7.102 203915_at CXCL9 NM_002416 chemokine (CXC motif) ligand 9 6.938 222162_s_at ADAMTS1 AK023795 a disintegrinlike and metalloprotease (reprolysin type) with thrombospondin type 1 motif, 1 6.931 205890_s_at UBD NM_006398 ubiquitin D 6.813 222885_at EMCN AF205940 endomucin -

(Indels) of the ATBF1 Gene and Their Effects on Growth-Related Traits in Three Indigenous Goat Breeds
Arch. Anim. Breed., 61, 311–319, 2018 https://doi.org/10.5194/aab-61-311-2018 Open Access © Author(s) 2018. This work is distributed under the Creative Commons Attribution 4.0 License. Archives Animal Breeding Detection of insertion/deletions (indels) of the ATBF1 gene and their effects on growth-related traits in three indigenous goat breeds Zhenyu Wei1,*, Ke Wang1,*, Yiqing Hui1, Hailong Yan1,2,3, Haijing Zhu2,3, Lei Qu2,3, Chuanying Pan1, Hong Chen1, and Xianyong Lan1 1College of Animal Science and Technology, Northwest A&F University, Shaanxi Key Laboratory of Molecular Biology for Agriculture, Yangling, Shaanxi, China 2Shaanxi Provincial Engineering and Technology Research Center of Cashmere Goats,Yulin University, Yulin, China 3Life Science Research Center, Yulin University, Yulin, China *These authors contributed equally to this work. Correspondence: Xianyong Lan ([email protected]) Received: 3 April 2018 – Revised: 23 June 2018 – Accepted: 11 July 2018 – Published: 26 July 2018 Abstract. The AT motif-binding factor (ATBF1), also known as zinc finger homeobox 3 (ZFXH3), is necessary for activating the POU1F1 gene; thus, the ATBF1 gene greatly affects the grow traits in animals. The objective of this work was to explore novel indel (insertion/deletion) variations and their associations with growth traits in three native Chinese goat breeds. Two indels within the ATBF1 gene were found in the Shaanbei white cashmere goat (SWCG; n D 581), the Guanzhong dairy goat (GZDG; n D 334) and the Hainan black goat (HNBG; n D 270) for the first time using 12 pairs of primers. Association analysis revealed that the P1-12-bp indel was consistently correlated with the body height of the three breeds, and individuals with ID (insertion/deletion) and DD (deletion/deletion) genotypes had a higher body weight than the II (insertion/insertion) genotype (P D 0:036); the P11-6-bp indel was consistently correlated with chest circumference and hip width of the three breeds. -

BMC Biology Biomed Central
BMC Biology BioMed Central Research article Open Access Classification and nomenclature of all human homeobox genes PeterWHHolland*†1, H Anne F Booth†1 and Elspeth A Bruford2 Address: 1Department of Zoology, University of Oxford, South Parks Road, Oxford, OX1 3PS, UK and 2HUGO Gene Nomenclature Committee, European Bioinformatics Institute (EMBL-EBI), Wellcome Trust Genome Campus, Hinxton, Cambridgeshire, CB10 1SA, UK Email: Peter WH Holland* - [email protected]; H Anne F Booth - [email protected]; Elspeth A Bruford - [email protected] * Corresponding author †Equal contributors Published: 26 October 2007 Received: 30 March 2007 Accepted: 26 October 2007 BMC Biology 2007, 5:47 doi:10.1186/1741-7007-5-47 This article is available from: http://www.biomedcentral.com/1741-7007/5/47 © 2007 Holland et al; licensee BioMed Central Ltd. This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Abstract Background: The homeobox genes are a large and diverse group of genes, many of which play important roles in the embryonic development of animals. Increasingly, homeobox genes are being compared between genomes in an attempt to understand the evolution of animal development. Despite their importance, the full diversity of human homeobox genes has not previously been described. Results: We have identified all homeobox genes and pseudogenes in the euchromatic regions of the human genome, finding many unannotated, incorrectly annotated, unnamed, misnamed or misclassified genes and pseudogenes.