Geometry, Kinematics, Exhumation, and Sedimentation of the Northern Bolivian Fold-Thrust-Belt-Foreland Basin System
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-
11677671 02.Pdf
DEPARTAMENTO DE LA PAZ N E D L A R R U T I IXIAMAS LEGEND TUMUPASA Department Province SAN JOSE DE Capital of Canton CHUPUAMONAS RURRENABAQUE LEGEND SAN BUENA F R A N Z VENTURA T/L 230kV(Exist. 2000) T/L 115kV(Exist. 2000) PATA SAN MOJOS ANTONIO T/L 69kv(Exist. 2000) SANTA CRUZ DEL T/L 34.5kv(Exist. 2000) VALLE AMENO T A M A Y T/L 24.9kv(Exist. 2000) T/L 19.9kv(Exist. 2000) O T/L 14.4kv(Exist. 2000) APOLO PELECHUCO SUCHES PULI ANTAQUILA DE IMPLEMENTATION PLAN BY RENEWABLE ENERGY PLAN BY RENEWABLE IMPLEMENTATION COPACABANA ATEN JAPAN INTERNATIONAL COOPERATION AGENCY COOPERATION INTERNATIONAL JAPAN ULLA ULLA THE STUDY ON RURAL ELECTRIFICATION ELECTRIFICATION THE STUDY ON RURAL TAYPI CUNUMA CAMSAYA CALAYA KAPNA OPINUAYA CURVA LAGUNILLASAAVEDRA GRAL. J.J. PEREZ CHULLINA STA. ROSA DE CAATA CHARI GRAL. RAMON CARIJANA IN THE REPUBLIC OF BOLIVIA GONZALES CAMATA YUCUMO AMARETE MAPIRI VILLA ROSARIO CAMAC DE WILACALA PUSILLANI CONSATA MARIAPU INICUA BAJO MOCOMOCO AUCAPATA SARAMPIUNI TUILUNI AYATA HUMANATA PAJONAL CHUMA VILAQUE ITALAQUE SUAPI DE ALTO BENI SAN JUAN DE CANCANI LIQUISANI COLLABAMBA GUANAY COTAPAMPA TEOPONTE PUERTO ACOSTA CHINAÑA 6 SANTA ROSA DE AGOSTO ANANEA CARGUARANI PAUCARES CHAJLAYA BELEN SANTA ANA DEL TAJANI PTO. ESCOMA MUÑECAS130 PANIAGUA ALTO BENI ANBANA TACACOMA PARAJACHI YANI H QUIABAYA LARECAJATIPUANI PALOS BLANCOS V. PUNI SANTA ROSA DE CHALLANA COLLASUYO SAN MIGUELO CALAMA I EDUARDO AVAROA DE YARICOA TIMUSI OBISPO BOSQUE CALLAPATA SOCOCONI VILLA ELEVACION PTO. CARABUCO CARRASCO LA RESERVAV CHUCHULAYA ANKOMA SAPUCUNI ALTO ILLIMANI ROSARIO 112 SORATA CARRASCO ENTRE RIOS PTO. -

5945-Iii-Penas.Pdf
- BOLIVIA 1:50.000 PENAS HOJA 5945 III MINA NATIVIDAD 13 KM. AGENCIA MINA PALCOCO 7 KM. 5 68 30' 54 55 56 57 58 59 560 61 62 25' 63 64 5 20' 80 16 30' 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 68 15' 4464 16 30' Cmdad Aluvion 4566 Cerro Nazacara LAGUNA Bofedal Huancuyo Cerro Kamaqueni Parqui Cerro Jankho Khala 5064 Estancia Parque KHARA KKOTA PACOLLA 12 Cabana 12 12 Estancia Hichu Kkota SORA CUCHO Cerro Penas Cunca KELWANA KKOTA WICHINCALCOTA 4946 Cerro Janchallani Capilla Santa Barbara Cerro Kilan Churu Estancia Escuela SATOCO Cerro Maru Khollu 4462 Cerro Chiar Khala PUCUN KHALA Comador 4200 Cmdad San Agustin 4014 Cruzani Loma Huari Lipina CUMBRANA Cerro Lapucho 11 Aluvi¢n 11 11 Capilla Exaltacion 5054 Ruinas HICHU KKOTA LAGUNA Cerro Jipara Cem PAMPA ESTANCIA SORA KKOTA LAGUNA 5229 SURA TIRA SISTHANA Ruinas Loma Cruzani Cerro Jankalluisa SORA PATILLA 5328 CONDOR HUMANA 4592 82 82 10 10 Corral 10 Comunidad Alto Penas Estancia Pastizal LAGUNA JURI KKOTA Vado 4424 WILLKKI PATA Pacuni Cerro Milluni 4306 Cerro Jachcha Jipina Cerro Huari Umana LAGUNA LLACHU KKOTA 4968 Escuela Gualberto Villarroel Vado Cerro Tira Kkollu 4950 4468 Vado 09 09 09 Capilla Ascencion 4832 Vado LACAYA PATA Comunidad Corral KHALA SIRCA Isquilllani LAGUNA HUANKHUNI KANLLAN KKOTA LAGUNA Cerro Paco Thojo Vado COCOTA TAYPI CHACA Cerro Japuchu Loma JACHA TIRA 4584 4884 08 08 PAMPA UMA TOMAS PUNCU JOKHO 08 Vado CHIAR KHOLLU Cerro Kollpani Vado 4304 Escuela Uma Tomas 4926 Vado Vado Pastizal LAGUNA LAKHO KKOTA Pastizal Cerro Quimsa Puiru OVEJHUYO Cerro Cashtanshiari 07 -

Las Relaciones Entre El Perú Y Bolivia (1826-2013)
Fabián Novak Sandra Namihas SERIE: POLÍTICA EXTERIOR PERUANA LAS RELACIONES ENTRE EL PERÚ Y BOLIVIA ( 1826-2013 ) SERIE: POLÍTICA EXTERIOR PERUANA LAS RELACIONES ENTRE EL PERÚ Y BOLIVIA (1826-2013) Serie: Política Exterior Peruana LAS RELACIONES ENTRE EL PERÚ Y BOLIVIA (1826-2013) Fabián Novak Sandra Namihas 2013 Serie: Política Exterior Peruana Las relaciones entre el Perú y Bolivia (1826-2013) Primera edición, octubre de 2013 © Konrad Adenauer Stiftung General Iglesias 630, Lima 18 – Perú Email: [email protected] URL: <www.kas.de/peru> Telf: (51-1) 208-9300 Fax: (51-1) 242-1371 © Instituto de Estudios Internacionales (IDEI) Pontificia Universidad Católica del Perú Plaza Francia 1164, Lima 1 – Perú Email: [email protected] URL: <www.pucp.edu.pe/idei> Telf: (51-1) 626-6170 Fax: (51-1) 626-6176 Diseño de cubierta: Eduardo Aguirre / Sandra Namihas Derechos reservados, prohibida la reproducción de este libro por cualquier medio, total o parcialmente, sin permiso expreso de los editores. Hecho el depósito legal en la Biblioteca Nacional del Perú Registro: Nº 2013-14683 ISBN Nº 978-9972-671-18-0 Impreso en: EQUIS EQUIS S.A. RUC: 20117355251 Jr. Inca 130, Lima 34 – Perú Impreso en el Perú – Printed in Peru A la memoria de mi padre y hermano, F.N. A mis padres, Jorge y María Luisa S.N. Índice Introducción …………………………….……...…………….…… 17 CAPÍTULO 1: El inicio de ambas repúblicas y los grandes temas bilaterales en el siglo XIX ……………………….………..……… 19 1 El inicio de las relaciones diplomáticas y el primer intento de federación peruano-boliviana ……………............. 22 2 El comienzo del largo camino para la definición de los límites ……………………………………………...…. -

El Ciclo De Los Bicentenarios En Bolivia
Este libro forma parte del acervo de la Biblioteca Jurídica Virtual del Instituto de Investigaciones Jurídicas de la UNAM www.juridicas.unam.mx Libro completo en: https://biblio.juridicas.unam.mx/bjv https://goo.gl/py4fme Las independencias iberoamericanas Bibliografía Galasso, Norberto, Mariano Moreno y la revolución nacional, Buenos Aires, Ed. Goyoacan, 1963. Halperin Donghi, Tulio, Revolución y guerra: formación de una elite dirigente en la Argentina criolla, Ed. Siglo XXI, 1994. ———————, Historia contemporánea de América Latina, Ed. Alianza, 1994. ———————, De la revolución de independencia a la confedera- ción rosista, Buenos Aires, Ed. Paidós, 2000. Puiggros, Rodolfo, Historia crítica de los partidos políticos argentinos, El ciclo de los bicentenarios Ed. Álvarez, 1965. en Bolivia ———————, Mariano Moreno y la revolución democrática argentina, Ed. Problemas, 1941. Iviça Tadic Pereira* Ramos, Jorge Abelardo, Revolución y contrarrevolución en la Argen- tina: las masas en nuestra historia, Ed. Amerindia, 1957. Zapata, Federico, MERCOSUR, tan joven y tan viejo, Argentina, 2006. Contexto histórico mundial Para mediados del siglo XViii, el sistema económico y político que había regido el mundo occidental durante varios siglos estaba agotado. Ya en la Europa del siglo XViii, como consecuencia de la incapacidad de las clases gobernantes —nobleza, clero y burgue- sía— para hacer frente a los problemas de Estado, la indecisión de la monarquía, los excesivos impuestos que recaían sobre los vasa- llos, el empobrecimiento de la población y la profunda corrupción determinaron el agotamiento del sistema y el surgimiento de una corriente filosófica crítica —la Ilustración, también denominada en- ciclopedismo— que afirmaba el poder ilimitado de la Razón para * Economista e historiadora, responsable de Bibliotecas Especializadas, Dirección de Patrimonio Tangible y Natural, Gobierno Municipal de La Paz-Bolivia. -

“Plan De Desarrollo De La Actividad Turistica En El Municipio De La Asunta”
“PLAN DE DESARROLLO DE LA ACTIVIDAD TURÍSTICA DEL MUNICIPIO DE LA ASUNTA” UNIVERSIDAD MAYOR DE SAN ANDRES FACULTAD DE HUMANIDADES Y CIENCIAS DE LA EDUCACION CARRERA DE TURISMO PROYECTO DE GRADO “PLAN DE DESARROLLO DE LA ACTIVIDAD TURISTICA EN EL MUNICIPIO DE LA ASUNTA” POSTULANTES: Univ. JUAN DANIEL CHURA TRIGO Univ. MABEDDY E. VILLCA SANDOVAL TUTOR: Lic. LUIS AMERICO TRINO TRUJILLO LA PAZ – BOLIVIA 2016 1 “PLAN DE DESARROLLO DE LA ACTIVIDAD TURÍSTICA DEL MUNICIPIO DE LA ASUNTA” PLAN DE DESARROLLO DE LA ACTIVIDAD TURÍSTICA EN EL MUNICIPIO DE LA ASUNTA El presente proyecto de grado se elaboró con el fin de diversificar la actividad económica del Municipio y de esta manera desarrollar el turismo y esta sea una actividad complementaria al cultivo de la hoja de coca en La Asunta. El problema el principal que se identificó es que: “En el municipio de La Asunta no existe un Plan de Desarrollo de la actividad Turística, que incide en un escaso flujo turístico hacia el Municipio. Se desarrolló una investigación consistente en entrevistas a los actores del tema turístico y se realizó una encuesta para definir objetivos prioritarios en los programas de desarrollo turístico. Una vez realizado el trabajo de campo se propone los siguientes programas: El programa I: Inventariación y Señalización de Atractivos Turísticos Programa II: Capacitación Turística a prestadores de servicios hospedaje, alimentación, transporte y guías locales. El programa III Diversificación de la oferta turística. El programa IV: Marketing y promoción turística, con proyectos de Diseño de la Imagen Corporativa del Municipio y proyecto Diseño del Portal Virtual. -

FORMATO 18X26 ESTUDIO.Indd
ESTUDIO DE NIÑAS Y ADOLESCENTES EN MATRIMONIOS Y UNIONES FORZADAS A TEMPRANA EDAD A TEMPRANA Y UNIONES FORZADAS ESTUDIO DE NIÑAS Y ADOLESCENTES EN MATRIMONIOS CYANMAGENTA AMARILLO NEGRO OT: 1666 CLIENTE: TAPA UNFPA FECHA: 27-02-20 MATERIAL Y GRAMAJE: COUCHE MATE 300 GR. TAMAÑO 36,7 X 26 CM. TIRAJE: UNI. 500 FORMATO: TIRA TAPAS ESTUDIO DE NIÑAS Y ADOLESCENTES/TIRA Ficha Bibliográfica Título: Estudio de niñas y adolescentes en matrimonios y uniones forzadas a temprana edad, en municipios seleccionados de Bolivia. Autor: Fondo de Población de las Naciones Unidas (UNFPA), Plan International INC. 136 pag Descriptores: GÉNERO/ NIÑAS/ ADOLESCENTES/ EMBARAZO INFANTIL/ UNIONES TEMPRANAS FORZADAS/ VIOLENCIA/ EMBARAZO EN LA ADOLESCENCIA / BOLIVIA. Elaborado por: Fondo de Población de las Naciones Unidas - UNFPA Plan International INC. Equipo de Investigación: María Dolores Castro, (Coordinadora de equipo) Franklin García, Cristina Rentería, Lorena Tapia, Teresa Ayala, Adrián Aliaga, Edwin Choque y Robin Mamani. Observatorio de Mortalidad Materna y Neonatal (OMMN) - CIDES, UMSA. Ilustraciones: 3K IMPRESIONES & PUBLICIDAD Diseño: ATÓMICAMARIA S.R.L. Impresión: General Internacional S.R.L. Depósito legal: 4-1-578-20 Esta publicación es posible gracias al apoyo financiero de la Embajada de Suecia en Bolivia. Se permite la reproducción total o parcial de la información aquí publicada, siempre que no sea alterada y se asignen los créditos correspondientes. Esta publicación es de distribución gratuita. Prohibida su venta. La Paz - Bolivia 2020 ESTUDIO DE -

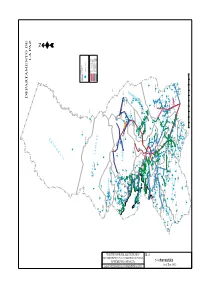
Maps and Database of Quaternary Faults in Bolivia and Chile
U.S. Department of the Interior U.S. Geological Survey Maps and Database of Quaternary Faults in Bolivia and Chile By Alain Lavenu, Ricardo Thiele, Michael N. Machette, Richard L. Dart, Lee-Ann Bradley and Kathleen M. Haller Open-File Report 00-283 This report is preliminary and has not been reviewed for conformity with U.S. Geological Survey editorial standards nor with the North American Stratigraphic Code. Any use of trade names in this publication is for descriptive purposes only and does not imply endorsement by the U.S. Geological Survey. 2000 1 Map and Database of Quaternary Faults in Bolivia and Chile A project of the International Lithosphere Program Task Group II-2, Major Active Faults of the World Proyecto Internacional de la Litósfera, Grupo de Trabajo II-2, Principales Fallas Activas del Mundo Data and map compiled by Datos y mapa compilado por 1 ALAIN LAVENU, 2RICARDO THIELE, 3 MICHAEL N. MACHETTE, 3 RICHARD L. DART, 3LEE-ANN BRADLEY, AND 3 KATHLEEN M. HALLER 1 IRD (Institut de Recherche pour le Développement) 213 rue La Fayette 75480 Paris, cedex 10, France 2 Departamento de Geología 3 U.S. Geological Survey Universidad de Chile Central Geologic Hazards Team Casilla 13518, Correo 21 MS 966, P.O. Box 25046 Santiago, Chile Denver, Colorado, USA Regional Coordinator for South America Coordinador Regionale por Sur America CARLOS COSTA Universidad Nacional de San Luis Departamento de Geología Casilla de Correo 320 San Luis, Argentina ILP Task Group II-2 Co-Chairman, Western Hemisphere ILP Grupo de Trabajo II-2 Co-Chairman, Hemisferio Occidental MICHAEL MACHETTE U.S. -

New Data on Tectonics of Bolivian Andes from a Photograph by Gemini 5, and Field Knowledges
[Trav. Lab. Gébl. Grenoble, t. 42, 1966] New data on Tectonics of Bolivian Andes from a photograph by Gemini 5, and field knowledges by Luigi RADELLI To my children, who will fly among the planets. ABSTRACT : A photograph taken by Gemini 5 shows many of the basic géomorphologie units of Bolivian Andes, which are : the Western volcanic Cordiller.a; the Altiplano with the lakes of Titikaka and Poopo, and <the Sait lakes of Uyuni and Coipasa; the Huayllamarca Range; the Eastern Cordilleras, including Cordillera Real; and the Sub Andean Zone. The whole of Bolivian Andes is eut by several tectonic lines, either paraHel or transverse to the géographie trend of the mountain ranges, some ones of which were revealed first by the photograph taken from Gemini 5. The tectonic lines (Coniri, Ichilo-Achacachi, Poopo, Palca, Chacarilla, and Chiriquina) correspond to faults which were active ever since Paleozoic. Their existence is proved by précise both stratigraphie and tectonic remarks within the blocks separated by them- selves. Of those, the Poopo Line crosses the Andean géographie trend; the Ichilo-Achacachi one does also that between the town of Santa Gruz on the East and the Cordillera Real on the West, but then it becomes paraUel to this trend. The other ones are always parallel to it. Mutual movements of Andean blocks separated by the indicated intersecting faults occurred during géologie time are studied since Silurian, and they are summarized at S 18. Spécial attention is paid to both Hercynian and Nevadian tectonic movements. With regard to Bolivian Andes, the conclusion is attained that one Hercynian cordillera existed Eastwards of the actual Altiplano, ano'ther Westwards of it, and a minor third one in place of Altiplano itself, Eastwards of tihe actual Huayllamarca Range. -

Documento UNODC Programa País Para Bolivia 2016-2020
PROGRAMA PAÍS PARA BOLIVIA 2016-2020 Fortaleciendo la capacidad del Estado Plurinacional de Bolivia para prevenir el delito y responder a las amenazas interconectadas de la droga, de la delincuencia organizada y de la corrupción Oficina País de la UNODC en Bolivia Enero de 2017 Tabla de contenido Lista de abreviaciones ...................................................................................................................... 5 RESUMEN EJECUTIVO ....................................................................................................................... 6 I. Introducción ......................................................................................................................... 8 Proceso de desarrollo del Programa País .......................................................................................... 8 Objetivo del Programa País ............................................................................................................. 10 Estructura del Programa País .......................................................................................................... 10 II. Análisis del contexto ........................................................................................................... 11 Coca y Desarrollo Integral ............................................................................................................... 11 Salud y Fiscalización de Drogas ....................................................................................................... 11 Prevención -

Ministerio De Economía Y Finanzas Públicas Viceministerio De Presupuesto Y Contabilidad Fiscal 2017
MINISTERIO DE ECONOMÍA Y FINANZAS PÚBLICAS VICEMINISTERIO DE PRESUPUESTO Y CONTABILIDAD FISCAL 2017 MINISTERIO DE ECONOMÍA Y FINANZAS PÚBLICAS VICEMINISTERIO DE PRESUPUESTO Y CONTABILIDAD FISCAL 2017 ÍNDICE RESOLUCIÓN MINISTERIAL N° 536 ................................................................................................................ 1 CLASIFICADOR INSTITUCIONAL ...…………………………………………………………………………………………………………… 3 CLASIFICADOR DE RECURSOS POR RUBROS ‐ Versión Descriptiva .............................................................20 CLASIFICADOR POR OBJETO DEL GASTO ‐ Versión Descriptiva ...................................................................43 CLASIFICADOR DE GASTOS POR FINALIDAD Y FUNCIÓN ‐ Versión Sintética ..............................................81 CLASIFICADOR DE GASTOS POR FINALIDAD Y FUNCIÓN ‐ Versión Descriptiva ..........................................85 CLASIFICADOR DE FUENTES DE FINANCIAMIENTO ‐ Versión Sintética .................................................... 120 CLASIFICADOR DE FUENTES DE FINANCIAMIENTO ‐ Versión Descriptiva ................................................ 121 CLASIFICADOR DE ORGANISMOS FINANCIADORES ‐ Versión Sintética ................................................... 124 CLASIFICADOR DE ORGANISMOS FINANCIADORES ‐ Versión Descriptiva ............................................... 128 CLASIFICADOR DE SECTORES ECONÓMICOS ............................................................................................ 130 CLASIFICADOR GEOGRÁFICO ................................................................................................................... -
Clasificador Presupuestario
CLASIFICADORES PRESUPUESTARIOS ÍNDICE ¡Error! Marcador no definido. CLASIFICADOR INSTITUCIONAL ..................................................................................................................... 3 CLASIFICADOR DE RECURSOS POR RUBROS - Versión Descriptiva .............................................................20 CLASIFICADOR POR OBJETO DEL GASTO - Versión Descriptiva ...................................................................43 CLASIFICADOR DE GASTOS POR FINALIDAD Y FUNCIÓN – Versión Sintética ..............................................81 CLASIFICADOR DE GASTOS POR FINALIDAD Y FUNCIÓN - Versión Descriptiva ..........................................85 CLASIFICADOR DE FUENTES DE FINANCIAMIENTO - Versión Sintética .....................................................120 CLASIFICADOR DE FUENTES DE FINANCIAMIENTO - Versión Descriptiva .................................................121 CLASIFICADOR DE ORGANISMOS FINANCIADORES - Versión Sintética ....................................................124 CLASIFICADOR DE ORGANISMOS FINANCIADORES - Versión Descriptiva ................................................128 CLASIFICADOR DE SECTORES ECONÓMICOS .............................................................................................130 CLASIFICADOR GEOGRÁFICO .....................................................................................................................142 CLASIFICADOR INSTITUCIONAL Entidades Presupuestables Gestión 2018 COD. DENOMINACIÓN SIGLA ADMINISTRACIÓN PÚBLICA APUB ADMINISTRACIÓN -

El Cargo Del Kamani, Su Papel Cultural En La Comunidad Y Su Funcion En El Ciclo Agrario Aymara
UNIVERSIDAD MAYOR DE SAN ANDRES FACULTAD DE CIENCIAS SOCIALES CARRERA DE ANTROPOLOGÍA TESIS DE GRADO EL CARGO DEL KAMANI, SU PAPEL CULTURAL EN LA COMUNIDAD Y SU FUNCION EN EL CICLO AGRARIO AYMARA Estudio realizado en el Cantón Santiago de Llallagua, Municipio de Colquencha, Provincia Aroma La Paz Postulante: Jannet Mery Patzi Apaza Tutor: Dr. Bernard Fishermann La Paz- Bolivia 2017 DEDICATORIA A la luz de mis ojos, amorosa dadiva de mis creadores, mi motivación constante y a sus generaciones en el tiempo... Mi hijo Jhamil Nefi Patzi A mí amado compañero eterno, mi bendición celestial, mi fortaleza, la razón de mi alegría diaria… Mi esposo Juan Francisco Sanhueza Bravo Y a la memoria de mis uywiris (cuidadores) terrenales a quienes agradezco profundamente el legado cultural de mis ancestros aymaras. Mis abuelos Rafael Phaxipati natural de Tiwanaku (Com. Achuta) Enriqueta Mendoza Flores de Wiacha Aunque fallecidos seguimos conectados en sueños… AGRADECIMIENTOS A nuestro Padre y Madre celestiales, creadores de vida y mis orígenes preexistentes y por tenerme en esta parte de tu regazo yuspajara pachamama… A la familia que me cobija con cariño en La Paz, mi hermana mayor (mi madre sustituta) Ruth Patzi Apaza, su esposo Angel Layme y mis queridos sobrinos Marlenne Burgoa Patzi, Israel Rafael Patzi, Mireya Layme Pazi, Fabio Layme Patzi y mi nña esperanza…Alejandra Apaza Poma. A mi tutor de tesis Bernard Fishermann un jiliri, irpiri (un consejero guía) amigo, compañero de la inolvidable Rosa Maria Quiroga, Por toda la experiencia y enseñanza compartidas conmigo. A los informantes de esta investigación sin su compromiso nos sería posible este logro Informantes principales y meritorios: Sr.