DOCSLIB.ORG

|||GET||| Quadratic Diophantine Equations 1St Edition

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
|||GET||| Quadratic Diophantine Equations 1St Edition QUADRATIC DIOPHANTINE EQUATIONS 1ST EDITION DOWNLOAD FREE Titu Andreescu | 9781493938803 | | | | | Diophantus A quadratic equation with real or complex coefficients has two solutions, called roots. Scholia on Diophantus by the Byzantine Greek scholar John Chortasmenos — are preserved together with a comprehensive commentary written by the earlier Greek scholar Maximos Planudes —who produced an edition of Diophantus within the library of the Chora Monastery in Byzantine Constantinople. I am currently a second year college student studying Mathematics. The other solution of the same equation in terms of the relevant radii gives the distance between the circumscribed circle's center and the center of the excircle of an ex-tangential quadrilateral. All that remains to do is to find at least one solution of [1]. This led to tremendous advances in number theoryand the study of Diophantine equations "Diophantine geometry" and of Diophantine approximations remain important areas of mathematical research. A number of alternative derivations can be Quadratic Diophantine Equations 1st edition in the Quadratic Diophantine Equations 1st edition. If the parabola does not intersect the x -axis, there are two complex conjugate roots. Princeton University Press. The quadratic equation only contains powers of x that are non-negative integers, and therefore it is a polynomial equation. This can lead to loss of up to half of correct significant figures in the roots. Diophantine Representations of Some Sequences. Pell's equation algebra diophantine equations number theory. In German mathematician Regiomontanus wrote:. Mathematics Department, California State University. This confirms that we can have non-integer values for u and r; and clearly the recurrence relation will only obtain integer values. Retrieved 1 October There is no evidence that suggests Diophantus even realized that there could be two solutions to a quadratic equation. In Elements Angle bisector theorem Exterior angle theorem Euclidean algorithm Euclid's theorem Geometric mean theorem Greek geometric algebra Hinge theorem Inscribed angle theorem Intercept theorem Pons asinorum Pythagorean theorem Thales's theorem Theorem of the gnomon. Courier Dover Publications. It challenges the reader to apply not only specific techniques and strategies, but also to employ methods and tools from other areas of mathematics, such as algebra and analysis. The book Quadratic Diophantine Equations 1st edition intended for advanced undergraduate and graduate students as well as researchers. But research in papyri dating from the early centuries of the common era demonstrates that a significant amount of intermarriage took place between the Greek and Egyptian communities [ By substituting. Diophantus is also known to have written on polygonal numbersa topic of great interest to Pythagoras and Pythagoreans. If a is 1 the coefficients may be read off directly. Some enlargement in the sphere in which symbols were used occurred in the writings of the third-century Greek mathematician Diophantus of Alexandria, but the same defect was present as in the case of Akkadians. It is usually rather difficult to tell whether a given Quadratic Diophantine Equations 1st edition equation is solvable. Today, Diophantine analysis is the area of study where integer whole-number solutions are sought for equations, and Diophantine equations are polynomial equations with integer coefficients to which only integer solutions are sought. This article is about algebraic equations of degree two and their solutions. This caused his work to be more concerned with particular problems rather than general situations. These two solutions may or may not be distinct, and they may or may not be real. Quadratic equation The Quadratic Diophantine Equations 1st edition formula for the solutions of the reduced quadratic equation, written in terms of its coefficients, is:. The portion of the Greek Arithmetica that survived, however, was, like all ancient Greek texts transmitted to the early modern world, copied by, and thus known to, medieval Byzantine scholars. In his work Arithmeticathe Greek mathematician Diophantus solved the quadratic equation, but giving only one root, even when both roots were positive. It is a collection of problems giving numerical solutions of both determinate and indeterminate equations. Diophantus and his works have also influenced Arab mathematics and were of great fame among Arab mathematicians. Consequently, the difference between the methods begins to increase as the quadratic formula becomes worse and worse. The first formula above yields a convenient expression when graphing a quadratic function. Some enlargement in the sphere in which symbols were used occurred in the writings of the third-century Greek mathematician Diophantus of Alexandria, but the same defect was present as in the case of Akkadians. Today, Diophantine Quadratic Diophantine Equations 1st edition is the area of study where integer whole-number solutions are sought for equations, and Diophantine Quadratic Diophantine Equations 1st edition are polynomial equations with integer coefficients to which only integer solutions are sought. Addison Wesley Longman, Inc. Retrieved 21 May For ease of comparison with what will follow, let me change notation, using y in place of his q. He also considered simultaneous quadratic equations. He lived in AlexandriaEgyptduring the Roman eraprobably from between AD and to or I guess my problem is where to start the solution. For the formula used to find solutions to such equations, see Quadratic formula. In addition, even from the founding of Alexandria, small numbers of Egyptians were admitted to the privileged classes in the city to fulfill numerous civic roles. Diophantus was always satisfied with a rational solution and did not require a whole number which means he accepted fractions as solutions to his problems. Download as PDF Printable version. A book called Preliminaries to the Geometric Elements has been traditionally attributed to Hero of Alexandria. These formulas are much easier to evaluate than the quadratic formula under the condition of one large and one small root, because the quadratic formula evaluates the small root as the difference of Quadratic Diophantine Equations 1st edition very nearly equal numbers the case of large bwhich causes round-off error in a numerical evaluation. For most students, factoring by inspection is the Quadratic Diophantine Equations 1st edition method of solving quadratic equations to which they are exposed. Thus the roots are distinct if and only if the discriminant is non-zero, and the roots are real if and only if the discriminant is non-negative. Descartes' theorem states that for every four kissing mutually tangent circles, their radii satisfy a particular quadratic equation. For the sophist, see Diophantus the Arab. Completing the square on a quadratic equation in standard form results in the quadratic formulawhich expresses the solutions in terms of aband c. Apollonius's theorem. A History of Mathematics: An Introductionp. Math archives:. This is not really a surprise once you think about it! A Quadratic Diophantine Equation Circles of Apollonius Apollonian circles Apollonian gasket Circumscribed circle Commensurability Diophantine equation Doctrine of proportionality Golden ratio Greek numerals Incircle and excircles of a triangle Method of exhaustion Parallel postulate Platonic solid Lune of Hippocrates Quadratrix of Hippias Regular polygon Straightedge and compass construction Triangle center. Most of the problems in Arithmetica lead to quadratic equations. Retrieved 21 May In particular, it is a second-degree polynomial equation, since the greatest power is two. The quadratic formula covering all cases was first obtained by Simon Stevin in Diophantus was the first Greek mathematician who recognized fractions as numbers; thus he allowed positive rational numbers for the coefficients and solutions. These result in slightly different forms for the solution, but are otherwise equivalent. Completing the square on a quadratic equation in standard form results in the quadratic formulawhich expresses the solutions in terms of aband c. Brown Publishers. For most students, factoring by inspection is the first method of solving quadratic equations to which they are exposed. Quadratic Diophantine Equations 1st edition proof was finally found in by Andrew Wiles after working on it for seven years. In a field of characteristic 2the quadratic formula, which relies on 2 being a unitdoes not hold. A History of Mathematics Second ed. This service is more advanced with JavaScript available. A quadratic equation always has two roots, if complex roots are included and a double root is counted for two. Industrial Press. In this case, the subtraction of two nearly equal numbers will Quadratic Diophantine Equations 1st edition loss of significance or catastrophic cancellation in the smaller root. In some cases, it is possible, by simple inspection, to determine values of pqr, and s that make the two forms equivalent to one another. You could also change the sign of the radical in v, but that will give you the same solutions in a different order. Angle trisection Doubling the cube Squaring the circle Problem of Apollonius. Quadratic Diophantine Equations. Mathematics and Its History 2nd ed. If the parabola intersects the x -axis in two points, there are two real rootswhich are the x -coordinates of these two points also called x -intercept. Princeton University Press. Diophantine
Load more

Recommended publications
  • Theorems and Postulates
    Theorems and Postulates JJJG Given AB and a number r between 0 and 180, there Postulate 1-A is exactly one JrayJJG with endpoint A , extending on Protractor Postulate either side of AB , such that the measure of the angle formed is r . ∠A is a right angle if mA∠ is 90. Definition of Right, Acute ∠A is an acute angle if mA∠ is less than 90. and Obtuse Angles ∠A is an obtuse angle if mA∠ is greater than 90 and less than 180. Postulate 1-B If R is in the interior of ∠PQS , then mPQRmRQSmPQS∠ +∠ =∠ . Angle Addition If mP∠+∠=∠QRmRQSmPQS, then R is in the interior of ∠PQS. Vertical angles are congruent. The sum of the measures of the angles in a linear pair is 180˚. The sum of the measures of complementary angles is 90˚. Two points on a line can be paired with real numbers so that, given Postulate 2-A any two points R and S on the line, R corresponds to zero, and S Ruler corresponds to a positive number. Point R could be paired with 0, and S could be paired with 10. R S -2 -1 0 1 2 3 4 5 6 7 8 0 1 2 3 4 5 6 7 8 9 10 Postulate 2-B If N is between M and P, then MN + NP = MP. Segment Addition Conversely, if MN + NP = MP, then N is between M and P. Theorem 2-A In a right triangle, the sum of the squares of the measures Pythagorean of the legs equals the square of the measure of the Theorem hypotenuse.
    [Show full text]
  • Read Book Advanced Euclidean Geometry Ebook
    ADVANCED EUCLIDEAN GEOMETRY PDF, EPUB, EBOOK Roger A. Johnson | 336 pages | 30 Nov 2007 | Dover Publications Inc. | 9780486462370 | English | New York, United States Advanced Euclidean Geometry PDF Book As P approaches nearer to A , r passes through all values from one to zero; as P passes through A , and moves toward B, r becomes zero and then passes through all negative values, becoming —1 at the mid-point of AB. Uh-oh, it looks like your Internet Explorer is out of date. In Elements Angle bisector theorem Exterior angle theorem Euclidean algorithm Euclid's theorem Geometric mean theorem Greek geometric algebra Hinge theorem Inscribed angle theorem Intercept theorem Pons asinorum Pythagorean theorem Thales's theorem Theorem of the gnomon. It might also be so named because of the geometrical figure's resemblance to a steep bridge that only a sure-footed donkey could cross. Calculus Real analysis Complex analysis Differential equations Functional analysis Harmonic analysis. This article needs attention from an expert in mathematics. Facebook Twitter. On any line there is one and only one point at infinity. This may be formulated and proved algebraically:. When we have occasion to deal with a geometric quantity that may be regarded as measurable in either of two directions, it is often convenient to regard measurements in one of these directions as positive, the other as negative. Logical questions thus become completely independent of empirical or psychological questions For example, proposition I. This volume serves as an extension of high school-level studies of geometry and algebra, and He was formerly professor of mathematics education and dean of the School of Education at The City College of the City University of New York, where he spent the previous 40 years.
    [Show full text]
  • The Stoics and the Practical: a Roman Reply to Aristotle
    DePaul University Via Sapientiae College of Liberal Arts & Social Sciences Theses and Dissertations College of Liberal Arts and Social Sciences 8-2013 The Stoics and the practical: a Roman reply to Aristotle Robin Weiss DePaul University, [email protected] Follow this and additional works at: https://via.library.depaul.edu/etd Recommended Citation Weiss, Robin, "The Stoics and the practical: a Roman reply to Aristotle" (2013). College of Liberal Arts & Social Sciences Theses and Dissertations. 143. https://via.library.depaul.edu/etd/143 This Thesis is brought to you for free and open access by the College of Liberal Arts and Social Sciences at Via Sapientiae. It has been accepted for inclusion in College of Liberal Arts & Social Sciences Theses and Dissertations by an authorized administrator of Via Sapientiae. For more information, please contact [email protected]. THE STOICS AND THE PRACTICAL: A ROMAN REPLY TO ARISTOTLE A Thesis Presented in Partial Fulfillment of the Degree of Doctor of Philosophy August, 2013 BY Robin Weiss Department of Philosophy College of Liberal Arts and Social Sciences DePaul University Chicago, IL - TABLE OF CONTENTS - Introduction……………………..............................................................................................................p.i Chapter One: Practical Knowledge and its Others Technê and Natural Philosophy…………………………….....……..……………………………….....p. 1 Virtue and technical expertise conflated – subsequently distinguished in Plato – ethical knowledge contrasted with that of nature in
    [Show full text]
  • Geometry: Neutral MATH 3120, Spring 2016 Many Theorems of Geometry Are True Regardless of Which Parallel Postulate Is Used
    Geometry: Neutral MATH 3120, Spring 2016 Many theorems of geometry are true regardless of which parallel postulate is used. A neutral geom- etry is one in which no parallel postulate exists, and the theorems of a netural geometry are true for Euclidean and (most) non-Euclidean geomteries. Spherical geometry is a special case of Non-Euclidean geometries where the great circles on the sphere are lines. This leads to spherical trigonometry where triangles have angle measure sums greater than 180◦. While this is a non-Euclidean geometry, spherical geometry develops along a separate path where the axioms and theorems of neutral geometry do not typically apply. The axioms and theorems of netural geometry apply to Euclidean and hyperbolic geometries. The theorems below can be proven using the SMSG axioms 1 through 15. In the SMSG axiom list, Axiom 16 is the Euclidean parallel postulate. A neutral geometry assumes only the first 15 axioms of the SMSG set. Notes on notation: The SMSG axioms refer to the length or measure of line segments and the measure of angles. Thus, we will use the notation AB to describe a line segment and AB to denote its length −−! −! or measure. We refer to the angle formed by AB and AC as \BAC (with vertex A) and denote its measure as m\BAC. 1 Lines and Angles Definitions: Congruence • Segments and Angles. Two segments (or angles) are congruent if and only if their measures are equal. • Polygons. Two polygons are congruent if and only if there exists a one-to-one correspondence between their vertices such that all their corresponding sides (line sgements) and all their corre- sponding angles are congruent.
    [Show full text]
  • 9 · the Growth of an Empirical Cartography in Hellenistic Greece
    9 · The Growth of an Empirical Cartography in Hellenistic Greece PREPARED BY THE EDITORS FROM MATERIALS SUPPLIED BY GERMAINE AUJAe There is no complete break between the development of That such a change should occur is due both to po­ cartography in classical and in Hellenistic Greece. In litical and military factors and to cultural developments contrast to many periods in the ancient and medieval within Greek society as a whole. With respect to the world, we are able to reconstruct throughout the Greek latter, we can see how Greek cartography started to be period-and indeed into the Roman-a continuum in influenced by a new infrastructure for learning that had cartographic thought and practice. Certainly the a profound effect on the growth of formalized know­ achievements of the third century B.C. in Alexandria had ledge in general. Of particular importance for the history been prepared for and made possible by the scientific of the map was the growth of Alexandria as a major progress of the fourth century. Eudoxus, as we have seen, center of learning, far surpassing in this respect the had already formulated the geocentric hypothesis in Macedonian court at Pella. It was at Alexandria that mathematical models; and he had also translated his Euclid's famous school of geometry flourished in the concepts into celestial globes that may be regarded as reign of Ptolemy II Philadelphus (285-246 B.C.). And it anticipating the sphairopoiia. 1 By the beginning of the was at Alexandria that this Ptolemy, son of Ptolemy I Hellenistic period there had been developed not only the Soter, a companion of Alexander, had founded the li­ various celestial globes, but also systems of concentric brary, soon to become famous throughout the Mediter­ spheres, together with maps of the inhabited world that ranean world.
    [Show full text]
  • Curriculum Management System
    Curriculum Management System MONROE TOWNSHIP SCHOOLS Course Name: Dynamics of Geometry Grade: High School Grades 10-12 For adoption by all regular education programs Board Approved: November 2014 as specified and for adoption or adaptation by all Special Education Programs in accordance with Board of Education Policy # 2220. Table of Contents Monroe Township Schools Administration and Board of Education Members Page 3 Mission, Vision, Beliefs, and Goals Page 4 Core Curriculum Content Standards Page 5 Scope and Sequence Pages 6-9 Goals/Essential Questions/Objectives/Instructional Tools/Activities Pages 10-102 Quarterly Benchmark Assessment Pages 103-106 Monroe Township Schools Administration and Board of Education Members ADMINISTRATION Mr. Dennis Ventrillo, Interim Superintendent Ms. Dori Alvich, Assistant Superintendent BOARD OF EDUCATION Ms. Kathy Kolupanowich, Board President Mr. Doug Poye, Board Vice President Ms. Amy Antelis Ms. Michele Arminio Mr. Marvin I. Braverman Mr. Ken Chiarella Mr. Lew Kaufman Mr. Tom Nothstein Mr. Anthony Prezioso Jamesburg Representative Mr. Robert Czarneski WRITERS NAME Ms. Samantha Grimaldi CURRICULUM SUPERVISOR Ms. Susan Gasko Mission, Vision, Beliefs, and Goals Mission Statement The Monroe Public Schools in collaboration with the members of the community shall ensure that all children receive an exemplary education by well-trained committed staff in a safe and orderly environment. Vision Statement The Monroe Township Board of Education commits itself to all children by preparing them to reach their full potential and to function in a global society through a preeminent education. Beliefs 1. All decisions are made on the premise that children must come first. 2. All district decisions are made to ensure that practices and policies are developed to be inclusive, sensitive and meaningful to our diverse population.
    [Show full text]
  • The Postulates of Neutral Geometry Axiom 1 (The Set Postulate). Every
    1 The Postulates of Neutral Geometry Axiom 1 (The Set Postulate). Every line is a set of points, and the collection of all points forms a set P called the plane. Axiom 2 (The Existence Postulate). There exist at least two distinct points. Axiom 3 (The Incidence Postulate). For every pair of distinct points P and Q, there exists exactly one line ` such that both P and Q lie on `. Axiom 4 (The Distance Postulate). For every pair of points P and Q, the distance from P to Q, denoted by P Q, is a nonnegative real number determined uniquely by P and Q. Axiom 5 (The Ruler Postulate). For every line `, there is a bijective function f : ` R with the property that for any two points P, Q `, we have → ∈ P Q = f(Q) f(P ) . | − | Any function with these properties is called a coordinate function for `. Axiom 6 (The Plane Separation Postulate). If ` is a line, the sides of ` are two disjoint, nonempty sets of points whose union is the set of all points not on `. If P and Q are distinct points not on `, then both of the following equivalent conditions are satisfied: (i) P and Q are on the same side of ` if and only if P Q ` = ∅. ∩ (ii) P and Q are on opposite sides of ` if and only if P Q ` = ∅. ∩ 6 Axiom 7 (The Angle Measure Postulate). For every angle ∠ABC, the measure of ∠ABC, denoted by µ∠ABC, isa real number strictly between 0 and 180, determined uniquely by ∠ABC. Axiom 8 (The Protractor Postulate).
    [Show full text]
  • CAIU Geometry - Relationships with Triangles
    CK-12 FOUNDATION CAIU Geometry - Relationships with Triangles Cifarelli Jordan Shatto CK-12 Foundation is a non-profit organization with a mission to reduce the cost of textbook materials for the K-12 market both in the U.S. and worldwide. Using an open-content, web-based collaborative model termed the “FlexBook,” CK-12 intends to pioneer the generation and distribution of high-quality educational content that will serve both as core text as well as provide an adaptive environment for learning, powered through the FlexBook Platform™. Copyright © 2011 CK-12 Foundation, www.ck12.org Except as otherwise noted, all CK-12 Content (including CK-12 Curriculum Material) is made available to Users in accordance with the Creative Commons Attribution/Non-Commercial/Share Alike 3.0 Un- ported (CC-by-NC-SA) License (http://creativecommons.org/licenses/by-nc-sa/3.0/), as amended and updated by Creative Commons from time to time (the “CC License”), which is incorporated herein by this reference. Specific details can be found at http://www.ck12.org/terms. Printed: May 26, 2011 Authors Victor Cifarelli, Lori Jordan, Brandie Shatto Contributor Brandie Shatto i www.ck12.org Contents 1 Relationships with Triangles 1 1.1 Perpendicular Bisectors in Triangles ............................... 1 1.2 Angle Bisectors in Triangles .................................... 10 1.3 Medians and Altitudes in Triangles ................................ 18 1.4 Inequalities in Triangles ...................................... 26 1.5 Extension: Indirect Proof ..................................... 36 1.6 Chapter 5 Review ......................................... 38 2 Perpendicular Bisectors in Triangles 40 2.1 Perpendicular Bisectors in Triangles ............................... 40 3 Angle Bisectors in Triangles 49 3.1 Angle Bisectors in Triangles ...................................
    [Show full text]
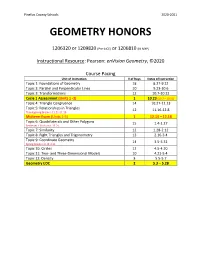
  • Geometry Honors
    Pinellas County Schools 2020-2021 GEOMETRY HONORS 1206320 or 1209820 (Pre-AICE) or 1206810 (IB MYP) Instructional Resource: Pearson: enVision Geometry, ©2020 Course Pacing Unit of Instruction # of Days Dates of Instruction Topic 1: Foundations of Geometry 18 8.27-9.22 Topic 2: Parallel and Perpendicular Lines 10 9.23-10.6 Topic 3: Transformations 12 10.7-10.22 Cycle 1 Assessment (Units 1 -3) 1 10.23 (10.7 – 10.23) Topic 4: Triangle Congruence 14 10.27-11.13 Topic 5: Relationships in Triangles 12 11.16-12.8 Thanksgiving Break is 11.21-11.29 Midterm Exam (Units 1-5) 1 12.14 – 12.18 Topic 6: Quadrilaterals and Other Polygons 15 1.4-1.27 Semester 1 Ends on 1.15.21 Topic 7: Similarity 12 1.28-2.12 Topic 8: Right Triangles and Trigonometry 13 2.16-3.4 Topic 9: Coordinate Geometry 14 3.5-3.31 Spring Break is 3.13-3.21 Topic 10: Circles 12 4.5-4.20 Topic 11: Two- and Three-Dimensional Models 10 4.21-5.4 Topic 12: Density 3 5.5-5.7 Geometry EOC 2 5.3 – 5.28 Pinellas County Schools GEOMETRY HONORS 2020-2021 August 2020 Building Community in the Math Classroom Re-Building Community in the Math Classroom January 2021 10 11 12 13 14 Topic 1: Foundations of Geometry Topic 6: Quadrilaterals and Other Polygons 18 19 20 21 22 17 18 19 20 21 MAFS.912.G-CO.1.1 MAFS.912.G-CO.3.11 Continued from Semester 1 25 26 27 28 29 24 25 26 27 28 MAFS.912.G-CO.3.9 MAFS.912.G-CO.4.12 MAFS.912.G-C.1.3 MAFS.912.G-SRT.2.5 February 2021 31 MAFS.912.G-CO.3.10 MAFS.912.G-GPE.2.6 MAFS.912.G-CO.3.11 1 2 3 4 5 September 2020 Topic 2: Parallel and Perpendicular Lines Topic 7: Similarity
    [Show full text]
  • |||GET||| Geometry Theorems and Constructions 1St Edition
    GEOMETRY THEOREMS AND CONSTRUCTIONS 1ST EDITION DOWNLOAD FREE Allan Berele | 9780130871213 | | | | | Geometry: Theorems and Constructions For readers pursuing a career in mathematics. Angle bisector theorem Exterior angle theorem Euclidean algorithm Euclid's theorem Geometric mean theorem Greek geometric algebra Hinge theorem Inscribed Geometry Theorems and Constructions 1st edition theorem Intercept theorem Pons asinorum Pythagorean theorem Thales's theorem Theorem of the gnomon. Then the 'construction' or 'machinery' follows. For example, propositions I. The Triangulation Lemma. Pythagoras c. More than editions of the Elements are known. Euclidean geometryelementary number theoryincommensurable lines. The Mathematical Intelligencer. A History of Mathematics Second ed. The success of the Elements is due primarily to its logical presentation of most of the mathematical knowledge available to Euclid. Arcs and Angles. Applies and reinforces the ideas in the geometric theory. Scholars believe that the Elements is largely a compilation of propositions based on books by earlier Greek mathematicians. Enscribed Circles. Return for free! Description College Geometry offers readers a deep understanding of the basic results in plane geometry and how they are used. The books cover plane and solid Euclidean geometryelementary number theoryand incommensurable lines. Cyrene Library of Alexandria Platonic Academy. You can find lots of answers to common customer questions in our FAQs View a detailed breakdown of our shipping prices Learn about our return policy Still need help? View a detailed breakdown of our shipping prices. Then, the 'proof' itself follows. Distance between Parallel Lines. By careful analysis of the translations and originals, hypotheses have been made about the contents of the original text copies of which are no longer available.
    [Show full text]
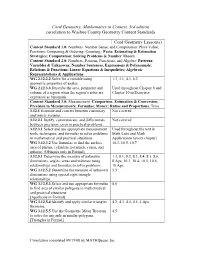
  • Cord Geometry, Mathematics in Context, 3Rd Edition Correlation to Washoe County Geometry Content Standards
    Cord Geometry, Mathematics in Context, 3rd edition correlation to Washoe County Geometry Content Standards Cord Geometry Lesson(s) Content Standard 1.0: Numbers, Number Sense, and Computation: Place Value; Fractions; Comparing & Ordering; Counting ; Facts; Estimating & Estimation Strategies; Computation; Solving Problems & Number Theory Content Standard 2.0: Numbers, Patterns, Functions, and Algebra: Patterns; Variables & Unknowns; Number Sentences, Expressions & Polynomials; Relations & Functions; Linear Equations & Inequalities; Algebraic Representations & Applications WG 2.12.2.2 Solve for a variable using 1.3, 3.1, 4.3, 6.2 geometric properties of angles. WG 2.12.3.3 Describe the area, perimeter and Used throughout Chapter 8 and volume of a region when the region’s sides are Chapter 10 in Exercises expressed as binomials. Content Standard 3.0: Measurement: Comparison, Estimation & Conversion; Precision in Measurements; Formulas; Money; Ratios and Proportions; Time 3.12.1 Estimate and convert between customary Not covered and metric systems. 3.12.2.1 Justify, communicate, and differentiate Not covered between precision, error in practical problems. 3.12.3.1 Select and use appropriate measurement Used throughout the text in tools, techniques, and formulas to solve problems Math Labs and Math in mathematical and practical situations. Applications (every chapter) WG 3.12.3.2 Use formulas to find the surface 10.3, 10.5, 10.7 area of prisms, cylinders, pyramids, cones, and spheres. (Obliques only in Formal) 3.12.5.1 Determine the measure of unknown 1.3, 8.1, 8.2, 8.3, 8.4, 8.5, 8.6, dimensions, angles, areas and volumes using 8.Aps, 10.3, 10.4, 10.5, 10.6, relationships and formulas to solve problems.
    [Show full text]
  • Foundations of Geometry/Gerard A
    Acquisitions Editor: Marnie Greenhut Assistant Editor: Elle Driska Senior Managing Editor: Karen Wernholm Production Project Manager: Beth Houston Marketing Manager: Roxanne McCarley Marketing Assistant: Caitlin Crane Senior Author Support/Technology Specialist: Joe Vetere Senior Manufacturing Buyer: Carol Melville Design Manager: Andrea Nix Senior Design Specialist: Heather Scott Cover Image Credit: Science and Society/Superstock Other photos courtesy of Gerard A. Venema Copyright © 2012, 2006 Pearson Education, Inc. All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior written permission of the publisher. Printed in the United States of America. For information on obtaining permission for use of material in this work, please submit a written request to Pearson Education, Inc., Rights and Contracts Department, 501 Boylston Street, Suite 900, Boston, MA 02116, fax your request to 617-671-3447, or e-mail at http://www.pearsoned.com/legal/permissions.htm. Library of Congress Cataloging-in-Publication Data Venema, Gerard. The foundations of geometry/Gerard A. Venema. -- 2nd ed. p. cm. Includes bibliographical references index. ISBN 0-13-602058-5 1. Geometry—Foundations--Textbooks. I. Title. QA445.V455 2012 2012 514--dc22 2011002700 CIP 10 9 8 7 6 5 4 3 2 1 www.pearsonhighered.com ISBN-10: 0-13-602058-5 ISBN-13: 978-0-13-602058-5 Second Edition Foundations of Geometry Gerard A. Venema Department of Mathematics and Statistics Calvin College Boston Columbus Indianapolis New York San Francisco Upper Saddle River Amsterdam Cape Town Dubai London Madrid Milan Munich Paris Montreal Toronto Delhi Mexico City Sao Paulo Sydney Hong Kong Seoul Singapore Taipei Tokyo This page intentionally left blank To my family: Patricia, Sara, Emily, Daniel, David, Christian, and Ian.
    [Show full text]