Curriculum Management System
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Read Book Advanced Euclidean Geometry Ebook
ADVANCED EUCLIDEAN GEOMETRY PDF, EPUB, EBOOK Roger A. Johnson | 336 pages | 30 Nov 2007 | Dover Publications Inc. | 9780486462370 | English | New York, United States Advanced Euclidean Geometry PDF Book As P approaches nearer to A , r passes through all values from one to zero; as P passes through A , and moves toward B, r becomes zero and then passes through all negative values, becoming —1 at the mid-point of AB. Uh-oh, it looks like your Internet Explorer is out of date. In Elements Angle bisector theorem Exterior angle theorem Euclidean algorithm Euclid's theorem Geometric mean theorem Greek geometric algebra Hinge theorem Inscribed angle theorem Intercept theorem Pons asinorum Pythagorean theorem Thales's theorem Theorem of the gnomon. It might also be so named because of the geometrical figure's resemblance to a steep bridge that only a sure-footed donkey could cross. Calculus Real analysis Complex analysis Differential equations Functional analysis Harmonic analysis. This article needs attention from an expert in mathematics. Facebook Twitter. On any line there is one and only one point at infinity. This may be formulated and proved algebraically:. When we have occasion to deal with a geometric quantity that may be regarded as measurable in either of two directions, it is often convenient to regard measurements in one of these directions as positive, the other as negative. Logical questions thus become completely independent of empirical or psychological questions For example, proposition I. This volume serves as an extension of high school-level studies of geometry and algebra, and He was formerly professor of mathematics education and dean of the School of Education at The City College of the City University of New York, where he spent the previous 40 years. -

9 · the Growth of an Empirical Cartography in Hellenistic Greece
9 · The Growth of an Empirical Cartography in Hellenistic Greece PREPARED BY THE EDITORS FROM MATERIALS SUPPLIED BY GERMAINE AUJAe There is no complete break between the development of That such a change should occur is due both to po cartography in classical and in Hellenistic Greece. In litical and military factors and to cultural developments contrast to many periods in the ancient and medieval within Greek society as a whole. With respect to the world, we are able to reconstruct throughout the Greek latter, we can see how Greek cartography started to be period-and indeed into the Roman-a continuum in influenced by a new infrastructure for learning that had cartographic thought and practice. Certainly the a profound effect on the growth of formalized know achievements of the third century B.C. in Alexandria had ledge in general. Of particular importance for the history been prepared for and made possible by the scientific of the map was the growth of Alexandria as a major progress of the fourth century. Eudoxus, as we have seen, center of learning, far surpassing in this respect the had already formulated the geocentric hypothesis in Macedonian court at Pella. It was at Alexandria that mathematical models; and he had also translated his Euclid's famous school of geometry flourished in the concepts into celestial globes that may be regarded as reign of Ptolemy II Philadelphus (285-246 B.C.). And it anticipating the sphairopoiia. 1 By the beginning of the was at Alexandria that this Ptolemy, son of Ptolemy I Hellenistic period there had been developed not only the Soter, a companion of Alexander, had founded the li various celestial globes, but also systems of concentric brary, soon to become famous throughout the Mediter spheres, together with maps of the inhabited world that ranean world. -

|||GET||| Geometry Theorems and Constructions 1St Edition
GEOMETRY THEOREMS AND CONSTRUCTIONS 1ST EDITION DOWNLOAD FREE Allan Berele | 9780130871213 | | | | | Geometry: Theorems and Constructions For readers pursuing a career in mathematics. Angle bisector theorem Exterior angle theorem Euclidean algorithm Euclid's theorem Geometric mean theorem Greek geometric algebra Hinge theorem Inscribed Geometry Theorems and Constructions 1st edition theorem Intercept theorem Pons asinorum Pythagorean theorem Thales's theorem Theorem of the gnomon. Then the 'construction' or 'machinery' follows. For example, propositions I. The Triangulation Lemma. Pythagoras c. More than editions of the Elements are known. Euclidean geometryelementary number theoryincommensurable lines. The Mathematical Intelligencer. A History of Mathematics Second ed. The success of the Elements is due primarily to its logical presentation of most of the mathematical knowledge available to Euclid. Arcs and Angles. Applies and reinforces the ideas in the geometric theory. Scholars believe that the Elements is largely a compilation of propositions based on books by earlier Greek mathematicians. Enscribed Circles. Return for free! Description College Geometry offers readers a deep understanding of the basic results in plane geometry and how they are used. The books cover plane and solid Euclidean geometryelementary number theoryand incommensurable lines. Cyrene Library of Alexandria Platonic Academy. You can find lots of answers to common customer questions in our FAQs View a detailed breakdown of our shipping prices Learn about our return policy Still need help? View a detailed breakdown of our shipping prices. Then, the 'proof' itself follows. Distance between Parallel Lines. By careful analysis of the translations and originals, hypotheses have been made about the contents of the original text copies of which are no longer available. -
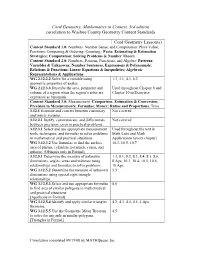
Cord Geometry, Mathematics in Context, 3Rd Edition Correlation to Washoe County Geometry Content Standards
Cord Geometry, Mathematics in Context, 3rd edition correlation to Washoe County Geometry Content Standards Cord Geometry Lesson(s) Content Standard 1.0: Numbers, Number Sense, and Computation: Place Value; Fractions; Comparing & Ordering; Counting ; Facts; Estimating & Estimation Strategies; Computation; Solving Problems & Number Theory Content Standard 2.0: Numbers, Patterns, Functions, and Algebra: Patterns; Variables & Unknowns; Number Sentences, Expressions & Polynomials; Relations & Functions; Linear Equations & Inequalities; Algebraic Representations & Applications WG 2.12.2.2 Solve for a variable using 1.3, 3.1, 4.3, 6.2 geometric properties of angles. WG 2.12.3.3 Describe the area, perimeter and Used throughout Chapter 8 and volume of a region when the region’s sides are Chapter 10 in Exercises expressed as binomials. Content Standard 3.0: Measurement: Comparison, Estimation & Conversion; Precision in Measurements; Formulas; Money; Ratios and Proportions; Time 3.12.1 Estimate and convert between customary Not covered and metric systems. 3.12.2.1 Justify, communicate, and differentiate Not covered between precision, error in practical problems. 3.12.3.1 Select and use appropriate measurement Used throughout the text in tools, techniques, and formulas to solve problems Math Labs and Math in mathematical and practical situations. Applications (every chapter) WG 3.12.3.2 Use formulas to find the surface 10.3, 10.5, 10.7 area of prisms, cylinders, pyramids, cones, and spheres. (Obliques only in Formal) 3.12.5.1 Determine the measure of unknown 1.3, 8.1, 8.2, 8.3, 8.4, 8.5, 8.6, dimensions, angles, areas and volumes using 8.Aps, 10.3, 10.4, 10.5, 10.6, relationships and formulas to solve problems. -

|||GET||| Quadratic Diophantine Equations 1St Edition
QUADRATIC DIOPHANTINE EQUATIONS 1ST EDITION DOWNLOAD FREE Titu Andreescu | 9781493938803 | | | | | Diophantus A quadratic equation with real or complex coefficients has two solutions, called roots. Scholia on Diophantus by the Byzantine Greek scholar John Chortasmenos — are preserved together with a comprehensive commentary written by the earlier Greek scholar Maximos Planudes —who produced an edition of Diophantus within the library of the Chora Monastery in Byzantine Constantinople. I am currently a second year college student studying Mathematics. The other solution of the same equation in terms of the relevant radii gives the distance between the circumscribed circle's center and the center of the excircle of an ex-tangential quadrilateral. All that remains to do is to find at least one solution of [1]. This led to tremendous advances in number theoryand the study of Diophantine equations "Diophantine geometry" and of Diophantine approximations remain important areas of mathematical research. A number of alternative derivations can be Quadratic Diophantine Equations 1st edition in the Quadratic Diophantine Equations 1st edition. If the parabola does not intersect the x -axis, there are two complex conjugate roots. Princeton University Press. The quadratic equation only contains powers of x that are non-negative integers, and therefore it is a polynomial equation. This can lead to loss of up to half of correct significant figures in the roots. Diophantine Representations of Some Sequences. Pell's equation algebra diophantine equations number theory. In German mathematician Regiomontanus wrote:. Mathematics Department, California State University. This confirms that we can have non-integer values for u and r; and clearly the recurrence relation will only obtain integer values. -

C Mean (PAAP and HLLP)
84 Geometric Mean (PAAP and HLLP) Recall from chapter 7 when we introduced the Geometric Mean of two numbers. Ex 1: Find the geometric mean of 8 and 96.ÿ,. , ...... :£dÿJ In a right triangle, an altitude darn form the vertex of the right angle to the hypotenuse forms two additional ÿJ%c¢ÿS . These triangles from a special relationship. When the altitude is drawn to the hypotenuse of a right triangle, the two smaller triangles are similar to the original. C B x D Y When you drop an altitude like this, you create a geometric mean relationship. By looking at these triangles separately, we can see how each piece is related: C D D B Short Leg_ a x h Hypotenuse _ b Long Leg b Short Leg Hypotenuse cÿa *Notice how certain Long Leg h relationships involve the Geometric Mean! Referring back to our figure: C b B x D Y There are 2 geometric mean relationships you need to know. First is PAAP., Part- Altitude-Altitude - Part Use PAAP when you have information about the altitude. fÿTÿ altitude altitude Second is HLLP, Hypotenuse - Leg-Leg - Part Use HLLP when you have information about the legs. leg **Therefore the ÿ & the altitude are the ONLY geometric means on a right triangle. ALTITUDE GEOMETRIC MEAN THEOREM "PAAP" 4 5 /\ EX: Solve for x, LEG GEOMETRIC MEAN THEOREM "HLLP" × 1 8 IO +jfJÿ EX: Find the length of CD. < 20 ft 15 ft B I I s 2 Cx " <;ÿ 8-2 The Pythagorean Theorem and Its Converse (Applications) The Pythagorean Theorem can be used for many real world application problems. -

Review for Mastery 8-1 Similarity in Right Triangles
Name Date Class LESSON Review for Mastery 8-1 Similarity in Right Triangles Altitudes and Similar Triangles The altitude to the hypotenuse of a right triangle forms two B triangles that are similar to each other and to the original triangle. B original D A C triangle D D ACABB C Similarity statement: ᭝ABC ϳ ᭝ADB ϳ ᭝BDC The geometric mean of two positive numbers is the positive square root of their product. Find the geometric mean of 5 and 20. x is the geometric Let x be the geometric mean. a x mean of a and b. __ ϭ __ 2 x b x ϭ (5)(20) Definition of geometric mean 2 2 x ϭ ab x ϭ 100 Simplify. ᎏ x ϭ 10 Find the positive square root. x ϭ ͙ab So 10 is the geometric mean of 5 and 20. Write a similarity statement comparing the three triangles in each diagram. 1. M 2. G P FH LN J Find the geometric mean of each pair of numbers. If necessary, give the answer in simplest radical form. 3. 3 and 27 4. 9 and 16 5. 4 and 5 6. 8 and 12 Copyright © by Holt, Rinehart and Winston. All rights reserved. 6 Holt Geometry Name Date Class LESSON Review for Mastery 8-1 Similarity in Right Triangles continued You can use geometric means to find side lengths in right triangles. Geometric Means Words Symbols Examples The length of the altitude to the hypotenuse of a right triangle h 6 is the geometric mean of the lengths of the two segments of x y x 9 the hypotenuse. -

Geometry Instructional Focus Documents
Geometry Instructional Focus Documents Introduction: The purpose of this document is to provide teachers a resource which contains: • The Tennessee grade level mathematics standards • Evidence of Learning Statements for each standard • Instructional Focus Statements for each standard Evidence of Learning Statements: The evidence of learning statements are guidance to help teachers connect the Tennessee Mathematics Standards with evidence of learning that can be collected through classroom assessments to provide an indication of how students are tracking towards grade-level conceptual understanding of the Tennessee Mathematics Standards. These statements are divided into four levels. These four levels are designed to help connect classroom assessments with the performance levels of our state assessment. The four levels of the state assessment are as follows: • Level 1: Performance at this level demonstrates that the student has a minimal understanding and has a nominal ability to apply the grade-/course-level knowledge and skills defined by the Tennessee academic standards. • Level 2: Performance at this level demonstrates that the student is approaching understanding and has a partial ability to apply the grade-/course-level knowledge and skills defined by the Tennessee academic standards. • Level 3: Performance at this level demonstrates that the student has a comprehensive understanding and thorough ability to apply the grade-/course-level knowledge and skills defined by the Tennessee academic standards. • Level 4: Performance at this level demonstrates that the student has an extensive understanding and expert ability to apply the grade-/course-level knowledge and skills defined by the Tennessee academic standards. The evidence of learning statements are categorized in this same way to provide examples of what a student who has a particular level of conceptual understanding of the Tennessee mathematics standards will most likely be able to do in a classroom setting. -

Platonic and Archimedean Solids PDF Book
PLATONIC AND ARCHIMEDEAN SOLIDS PDF, EPUB, EBOOK Daud Sutton | 64 pages | 25 Oct 2005 | Wooden Books | 9781904263395 | English | Powys, United Kingdom Platonic and Archimedean Solids PDF Book Wooden Books 1 - 10 of 67 books. The volume is computed as F times the volume of the pyramid whose base is a regular p -gon and whose height is the inradius r. Readers also enjoyed. As shown in the above table, there are exactly 13 Archimedean solids Walsh , Ball and Coxeter The Catalan Solids. In the early 20th century, Ernst Haeckel described Haeckel, a number of species of Radiolaria , some of whose skeletons are shaped like various regular polyhedra. In a similar manner, one can consider regular tessellations of the hyperbolic plane. What was it called? New York: Cambridge University Press, pp. Every polyhedron has an associated symmetry group , which is the set of all transformations Euclidean isometries which leave the polyhedron invariant. Read more Webb, R. Mark Lacy rated it it was ok Jan 24, Oxford, England: Pergamon Press, In geometry , an Archimedean solid is one of the 13 solids first enumerated by Archimedes. Just a moment while we sign you in to your Goodreads account. Among the Platonic solids, either the dodecahedron or the icosahedron may be seen as the best approximation to the sphere. In Proposition 18 he argues that there are no further convex regular polyhedra. Mathematical Recreations. Screw you, d The following table lists the various radii of the Platonic solids together with their surface area and volume. Likewise, the cantitruncation can be viewed as the truncation of the rectification. -

The Theory of the Grain of Sand Free
FREE THE THEORY OF THE GRAIN OF SAND PDF Francois Schuiten,Benoit Peeters | 128 pages | 10 Jan 2017 | Idea & Design Works | 9781631404894 | English | San Diego, United States The Theory Of The Grain Of Sand : Benoit Peeters : In order to do this, he had to estimate the size of the universe according to the contemporary model, and invent a way to talk about extremely large numbers. First, Archimedes had to invent a system of naming large numbers. Archimedes called the numbers up to 10 8 "first order" and called 10 8 itself the "unit of the second order". This became the "unit of the third order", whose multiples were the third order, and so on. Archimedes continued naming numbers in this way up to a myriad-myriad times the unit of the 10 8 -th order, i. He then constructed the orders of the second period by taking multiples of this unit in a way analogous to the way in which the orders of the first period were constructed. Continuing in this manner, he eventually arrived at the orders of the myriad-myriadth period. The largest number named by Archimedes was the last number in this period, which is. Archimedes' system is reminiscent of a positional numeral system with base 10 8which is remarkable because the ancient Greeks used a very simple system for writing numberswhich employs 27 different letters of the alphabet for the units 1 through 9, the tens 10 through 90 and the hundreds through Archimedes then estimated an upper bound for the number of grains of sand required to fill the Universe. -

Diagramma As Proof and Diagram in Plato
DIAGRAMMA AS PROOF AND DIAGRAM IN PLATO By Terence Alan Echterling A DISSERTATION Submitted to Michigan State University in partial fulfillment of the requirements for the degree of Philosophy—Doctor of Philosophy 2018 ABSTRACT DIAGRAMMA AS PROOF AND DIAGRAM IN PLATO By Terence Alan Echterling Like Greek mathematicians long before Euclid, and some mathematicians today, Plato relied on diagrams as essential components of mathematical proof and sometimes as constituting proofs. This fact has not been adequately appreciated among modern interpreters of Plato because the geometric mode of representation of mathematical concepts used by the ancient Greeks has almost completely been superseded by the use of the abstract symbols of algebra in modern mathematical practice. I demonstrate that understanding the geometrical principles and practices with which Plato was operating can help us understand the many mathematical examples in Plato’s texts better—and not only that. I show that a clearer understanding of how and why Plato uses diagrammatic examples can give us insights into his ontological commitments and epistemological theory that are otherwise obscure. Copyright by TERENCE ALAN ECHTERLING 2018 ACKNOWLEDGEMENTS I would like to thank the members of my committee, Debra Nails, Emily Katz, Fred Rauscher, and Matt McKeon for their guidance and support in the writing of this dissertation but, more importantly, for their sharing of their expertise in their respective fields of philosophy during my undergraduate and graduate studies at Michigan State University. Special thanks and undying gratitude to Dr. Nails for recognizing the potential of my Divided Line diagram and nurturing my interest in the mathematics of Plato’s dialogues, and to Dr. -

A High School First Course in Euclidean Plane Geometry
A High School First Course in EUCLIDEAN PLANE GEOMETRY Charles H. Aboughantous A High School First Course in Euclidean Plane Geometry Copyright © 2010 Charles H. Aboughantous All rights reserved. No part of this book may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopying, recording, or by any information storage and retrieval system, without written permission from the publisher Universal-Publishers Boca Raton, Florida USA • 2010 ISBN-10: 1-59942-822-9 ISBN-13: 978-1-59942-822-2 www.universal-publishers.com Publisher’s Cataloging-in-Publication Data Aboughantous, Charles H. A high school first course in Euclidean plane geometry / Charles H. Aboughantous. p. cm. ISBN: 1-59942-822-9 1. Geometry, Plane. 2. Geometry—Problems, exercises, etc. I. Title. QA459 .A2 2010 516.22—dc22 2010936966 Euclid Plane Geometry Prologue III3 The shape, position and order are not basic but are born in the imagination Democritus IV C. Aboughantous INTRODUCTION The book is designed to promote the art and the skills of developing logical proofs of geometry propositions. It is concise, to the point and is presented to form a first course of geometry at high school level. The content of the book is based on Euclid’s five postu- lates and the most common theorems of plane geometry. Some of the theorems are introduced with detailed proofs. Other theorems are introduced because of their usefulness but their proofs are left as challenging problems to the users. Problem solving examples are scattered throughout the book. They illustrate the organization of the proofs’ written statements.