(OLS) Consider the Following Simple Linear Regression Model Yi =
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
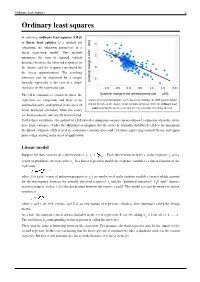
Ordinary Least Squares 1 Ordinary Least Squares
Ordinary least squares 1 Ordinary least squares In statistics, ordinary least squares (OLS) or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear approximation. The resulting estimator can be expressed by a simple formula, especially in the case of a single regressor on the right-hand side. The OLS estimator is consistent when the regressors are exogenous and there is no Okun's law in macroeconomics states that in an economy the GDP growth should multicollinearity, and optimal in the class of depend linearly on the changes in the unemployment rate. Here the ordinary least squares method is used to construct the regression line describing this law. linear unbiased estimators when the errors are homoscedastic and serially uncorrelated. Under these conditions, the method of OLS provides minimum-variance mean-unbiased estimation when the errors have finite variances. Under the additional assumption that the errors be normally distributed, OLS is the maximum likelihood estimator. OLS is used in economics (econometrics) and electrical engineering (control theory and signal processing), among many areas of application. Linear model Suppose the data consists of n observations { y , x } . Each observation includes a scalar response y and a i i i vector of predictors (or regressors) x . In a linear regression model the response variable is a linear function of the i regressors: where β is a p×1 vector of unknown parameters; ε 's are unobserved scalar random variables (errors) which account i for the discrepancy between the actually observed responses y and the "predicted outcomes" x′ β; and ′ denotes i i matrix transpose, so that x′ β is the dot product between the vectors x and β. -

Ordinary Least Squares: the Univariate Case
Introduction The OLS method The linear causal model A simulation & applications Conclusion and exercises Ordinary Least Squares: the univariate case Clément de Chaisemartin Majeure Economie September 2011 Clément de Chaisemartin Ordinary Least Squares Introduction The OLS method The linear causal model A simulation & applications Conclusion and exercises 1 Introduction 2 The OLS method Objective and principles of OLS Deriving the OLS estimates Do OLS keep their promises ? 3 The linear causal model Assumptions Identification and estimation Limits 4 A simulation & applications OLS do not always yield good estimates... But things can be improved... Empirical applications 5 Conclusion and exercises Clément de Chaisemartin Ordinary Least Squares Introduction The OLS method The linear causal model A simulation & applications Conclusion and exercises Objectives Objective 1 : to make the best possible guess on a variable Y based on X . Find a function of X which yields good predictions for Y . Given cigarette prices, what will be cigarettes sales in September 2010 in France ? Objective 2 : to determine the causal mechanism by which X influences Y . Cetebus paribus type of analysis. Everything else being equal, how a change in X affects Y ? By how much one more year of education increases an individual’s wage ? By how much the hiring of 1 000 more policemen would decrease the crime rate in Paris ? The tool we use = a data set, in which we have the wages and number of years of education of N individuals. Clément de Chaisemartin Ordinary Least Squares Introduction The OLS method The linear causal model A simulation & applications Conclusion and exercises Objective and principles of OLS What we have and what we want For each individual in our data set we observe his wage and his number of years of education. -

Chapter 2: Ordinary Least Squares Regression
Chapter 2: Ordinary Least Squares In this chapter: 1. Running a simple regression for weight/height example (UE 2.1.4) 2. Contents of the EViews equation window 3. Creating a workfile for the demand for beef example (UE, Table 2.2, p. 45) 4. Importing data from a spreadsheet file named Beef 2.xls 5. Using EViews to estimate a multiple regression model of beef demand (UE 2.2.3) 6. Exercises Ordinary Least Squares (OLS) regression is the core of econometric analysis. While it is important to calculate estimated regression coefficients without the aid of a regression program one time in order to better understand how OLS works (see UE, Table 2.1, p.41), easy access to regression programs makes it unnecessary for everyday analysis.1 In this chapter, we will estimate simple and multivariate regression models in order to pinpoint where the regression statistics discussed throughout the text are found in the EViews program output. Begin by opening the EViews program and opening the workfile named htwt1.wf1 (this is the file of student height and weight that was created and saved in Chapter 1). Running a simple regression for weight/height example (UE 2.1.4): Regression estimation in EViews is performed using the equation object. To create an equation object in EViews, follow these steps: Step 1. Open the EViews workfile named htwt1.wf1 by selecting File/Open/Workfile on the main menu bar and click on the file name. Step 2. Select Objects/New Object/Equation from the workfile menu.2 Step 3. -

Time-Series Regression and Generalized Least Squares in R*
Time-Series Regression and Generalized Least Squares in R* An Appendix to An R Companion to Applied Regression, third edition John Fox & Sanford Weisberg last revision: 2018-09-26 Abstract Generalized least-squares (GLS) regression extends ordinary least-squares (OLS) estimation of the normal linear model by providing for possibly unequal error variances and for correlations between different errors. A common application of GLS estimation is to time-series regression, in which it is generally implausible to assume that errors are independent. This appendix to Fox and Weisberg (2019) briefly reviews GLS estimation and demonstrates its application to time-series data using the gls() function in the nlme package, which is part of the standard R distribution. 1 Generalized Least Squares In the standard linear model (for example, in Chapter 4 of the R Companion), E(yjX) = Xβ or, equivalently y = Xβ + " where y is the n×1 response vector; X is an n×k +1 model matrix, typically with an initial column of 1s for the regression constant; β is a k + 1 ×1 vector of regression coefficients to estimate; and " is 2 an n×1 vector of errors. Assuming that " ∼ Nn(0; σ In), or at least that the errors are uncorrelated and equally variable, leads to the familiar ordinary-least-squares (OLS) estimator of β, 0 −1 0 bOLS = (X X) X y with covariance matrix 2 0 −1 Var(bOLS) = σ (X X) More generally, we can assume that " ∼ Nn(0; Σ), where the error covariance matrix Σ is sym- metric and positive-definite. Different diagonal entries in Σ error variances that are not necessarily all equal, while nonzero off-diagonal entries correspond to correlated errors. -

Chapter 2 Simple Linear Regression Analysis the Simple
Chapter 2 Simple Linear Regression Analysis The simple linear regression model We consider the modelling between the dependent and one independent variable. When there is only one independent variable in the linear regression model, the model is generally termed as a simple linear regression model. When there are more than one independent variables in the model, then the linear model is termed as the multiple linear regression model. The linear model Consider a simple linear regression model yX01 where y is termed as the dependent or study variable and X is termed as the independent or explanatory variable. The terms 0 and 1 are the parameters of the model. The parameter 0 is termed as an intercept term, and the parameter 1 is termed as the slope parameter. These parameters are usually called as regression coefficients. The unobservable error component accounts for the failure of data to lie on the straight line and represents the difference between the true and observed realization of y . There can be several reasons for such difference, e.g., the effect of all deleted variables in the model, variables may be qualitative, inherent randomness in the observations etc. We assume that is observed as independent and identically distributed random variable with mean zero and constant variance 2 . Later, we will additionally assume that is normally distributed. The independent variables are viewed as controlled by the experimenter, so it is considered as non-stochastic whereas y is viewed as a random variable with Ey()01 X and Var() y 2 . Sometimes X can also be a random variable. -

Regression Analysis
Regression Analysis Terminology Independent (Exogenous) Variable – Our X value(s), they are variables that are used to explain our y variable. They are not linearly dependent upon other variables in our model to get their value. X1 is not a function of Y nor is it a linear function of any of the other X variables. 2 Note, this does not exclude X2=X1 as another independent variable as X2 and X1 are not linear combinations of each other. Dependent (Endogenous) Variable – Our Y value, it is the value we are trying to explain as, hypothetically, a function of the other variables. Its value is determined by or dependent upon the values of other variables. Error Term – Our ε, they are the portion of the dependent variable that is random, unexplained by any independent variable. Intercept Term – Our α, from the equation of a line, it is the y-value where the best-fit line intercepts the y-axis. It is the estimated value of the dependent variable given the independent variable(s) has(have) a value of zero. Coefficient(s) – Our β(s), this is the number in front of the independent variable(s) in the model below that relates how much a one unit change in the independent variable is estimated to change the value of the dependent variable. Standard Error – This number is an estimate of the standard deviation of the coefficient. Essentially, it measures the variability in our estimate of the coefficient. Lower standard errors lead to more confidence of the estimate because the lower the standard error, the closer to the estimated coefficient is the true coefficient. -

Testing for Heteroskedastic Mixture of Ordinary Least 5
TESTING FOR HETEROSKEDASTIC MIXTURE OF ORDINARY LEAST 5. SQUARES ERRORS Chamil W SENARATHNE1 Wei JIANGUO2 Abstract There is no procedure available in the existing literature to test for heteroskedastic mixture of distributions of residuals drawn from ordinary least squares regressions. This is the first paper that designs a simple test procedure for detecting heteroskedastic mixture of ordinary least squares residuals. The assumption that residuals must be drawn from a homoscedastic mixture of distributions is tested in addition to detecting heteroskedasticity. The test procedure has been designed to account for mixture of distributions properties of the regression residuals when the regressor is drawn with reference to an active market. To retain efficiency of the test, an unbiased maximum likelihood estimator for the true (population) variance was drawn from a log-normal normal family. The results show that there are significant disagreements between the heteroskedasticity detection results of the two auxiliary regression models due to the effect of heteroskedastic mixture of residual distributions. Forecasting exercise shows that there is a significant difference between the two auxiliary regression models in market level regressions than non-market level regressions that supports the new model proposed. Monte Carlo simulation results show significant improvements in the model performance for finite samples with less size distortion. The findings of this study encourage future scholars explore possibility of testing heteroskedastic mixture effect of residuals drawn from multiple regressions and test heteroskedastic mixture in other developed and emerging markets under different market conditions (e.g. crisis) to see the generalisatbility of the model. It also encourages developing other types of tests such as F-test that also suits data generating process. -

Spatial Autocorrelation and Red Herrings in Geographical Ecology
UC Irvine UC Irvine Previously Published Works Title Spatial autocorrelation and red herrings in geographical ecology Permalink https://escholarship.org/uc/item/6jg661wx Journal Global Ecology and Biogeography, 12(1) ISSN 0960-7447 Authors Diniz, JAF Bini, L M Hawkins, Bradford A. Publication Date 2003 Peer reviewed eScholarship.org Powered by the California Digital Library University of California Global Ecology & Biogeography (2003) 12, 53–64 RESEARCH PAPER SpatialBlackwell Science, Ltd autocorrelation and red herrings in geographical ecology JOSÉ ALEXANDRE FELIZOLA DINIZ-FILHO*, LUIS MAURICIO BINI* and BRADFORD A. HAWKINS† *Departamento de Biologia Geral, ICB, Universidade Federal de Goiás, CP 131, 74 001–970, Goiânia, GO, Brazil; and †Department of Ecol- ogy and Evolutionary Biology, University of California, Irvine, CA 92697, U.S.A., E-mail: [email protected]; [email protected] ABSTRACT Results Bird richness is characterized by a quadratic north– south gradient. Spatial correlograms usually had positive Aim Spatial autocorrelation in ecological data can inflate autocorrelation up to c. 1600 km. Including the environmen- Type I errors in statistical analyses. There has also been a tal variables successively in the OLS model reduced spatial recent claim that spatial autocorrelation generates ‘red autocorrelation in the residuals to non-detectable levels, herrings’, such that virtually all past analyses are flawed. We indicating that the variables explained all spatial structure in consider the origins of this phenomenon, the implications of the data. In principle, if residuals are not autocorrelated then spatial autocorrelation for macro-scale patterns of species OLS is a special case of GLS. However, our comparison diversity and set out a clarification of the statistical problems between OLS and GLS models including all environmental generated by its presence. -

Bayesian Inference
Bayesian Inference Thomas Nichols With thanks Lee Harrison Bayesian segmentation Spatial priors Posterior probability Dynamic Causal and normalisation on activation extent maps (PPMs) Modelling Attention to Motion Paradigm Results SPC V3A V5+ Attention – No attention Büchel & Friston 1997, Cereb. Cortex Büchel et al. 1998, Brain - fixation only - observe static dots + photic V1 - observe moving dots + motion V5 - task on moving dots + attention V5 + parietal cortex Attention to Motion Paradigm Dynamic Causal Models Model 1 (forward): Model 2 (backward): attentional modulation attentional modulation of V1→V5: forward of SPC→V5: backward Photic SPC Attention Photic SPC V1 V1 - fixation only V5 - observe static dots V5 - observe moving dots Motion Motion - task on moving dots Attention Bayesian model selection: Which model is optimal? Responses to Uncertainty Long term memory Short term memory Responses to Uncertainty Paradigm Stimuli sequence of randomly sampled discrete events Model simple computational model of an observers response to uncertainty based on the number of past events (extent of memory) 1 2 3 4 Question which regions are best explained by short / long term memory model? … 1 2 40 trials ? ? Overview • Introductory remarks • Some probability densities/distributions • Probabilistic (generative) models • Bayesian inference • A simple example – Bayesian linear regression • SPM applications – Segmentation – Dynamic causal modeling – Spatial models of fMRI time series Probability distributions and densities k=2 Probability distributions -

Note 4: Statistical Properties of the OLS Estimators
ECONOMICS 351* -- NOTE 4 M.G. Abbott ECON 351* -- NOTE 4 Statistical Properties of the OLS Coefficient Estimators 1. Introduction ˆ We derived in Note 2 the OLS (Ordinary Least Squares) estimators β j (j = 0, 1) of the regression coefficients βj (j = 0, 1) in the simple linear regression model given by the population regression equation, or PRE Yi = β0 + β1Xi + ui (i = 1, …, N) (1) where ui is an iid random error term. The OLS sample regression equation (SRE) corresponding to PRE (1) is ˆ ˆ Yi = β0 + β1Xi + uˆ i (i = 1, …, N) (2) ˆ ˆ where β0 and β1 are the OLS coefficient estimators given by the formulas ˆ ∑i xi yi β1 = 2 (3) ∑i xi ˆ ˆ β0 = Y − β1X (4) xXii≡−X, yYii≡−Y, X= ∑ iiXN, and YY= ∑ iiN. Why Use the OLS Coefficient Estimators? The reason we use these OLS coefficient estimators is that, under assumptions A1- A8 of the classical linear regression model, they have several desirable statistical properties. This note examines these desirable statistical properties of the OLS ˆ coefficient estimators primarily in terms of the OLS slope coefficient estimator β1 ; ˆ the same properties apply to the intercept coefficient estimator β0 . ECON 351* -- Note 4: Statistical Properties of OLS Estimators ... Page 1 of 12 pages ECONOMICS 351* -- NOTE 4 M.G. Abbott 2. Statistical Properties of the OLS Slope Coefficient Estimator ˆ ¾ PROPERTY 1: Linearity of β1 ˆ The OLS coefficient estimator β1 can be written as a linear function of the sample values of Y, the Yi (i = 1, ..., N). -

R-Squared for Bayesian Regression Models⇤
R-squared for Bayesian regression models⇤ Andrew Gelman† Ben Goodrich‡ Jonah Gabry‡ Aki Vehtari§ 4 Nov 2018 Abstract The usual definition of R2 (variance of the predicted values divided by the variance of the data) has a problem for Bayesian fits, as the numerator can be larger than the denominator. We propose an alternative definition similar to one that has appeared in the survival analysis literature: the variance of the predicted values divided by the variance of predicted values plus the expected variance of the errors. 1. The problem Consider a regression model of outcomes y and predictors X with predicted values E(y X, ✓), fit | to data (X, y)n,n=1,...,N. Ordinary least squares yields an estimated parameter vector ✓ˆ with predicted valuesy ˆ =E(y X , ✓ˆ) and residual variance V N yˆ , where we are using the notation, n | n n=1 n N 1 V N z = (z z¯)2, for any vector z. n=1 n N 1 n − n=1 − X The proportion of variance explained, N 2 Vn=1 yˆn classical R = N , (1) Vn=1 yn is a commonly used measure of model fit, and there is a long literature on interpreting it, adjusting it for degrees of freedom used in fitting the model, and generalizing it to other settings such as hierarchical models; see, for example, Xu (2003) and Gelman and Pardoe (2006). Two challenges arise in defining R2 in a Bayesian context. The first is the desire to reflect posterior uncertainty in the coefficients, which should remove or at least reduce the overfitting problem of least squares. -

Chapter 11 Autocorrelation
Chapter 11 Autocorrelation One of the basic assumptions in the linear regression model is that the random error components or disturbances are identically and independently distributed. So in the model y Xu , it is assumed that 2 u ifs 0 Eu(,tts u ) 0 if0s i.e., the correlation between the successive disturbances is zero. 2 In this assumption, when Eu(,tts u ) u , s 0 is violated, i.e., the variance of disturbance term does not remain constant, then the problem of heteroskedasticity arises. When Eu(,tts u ) 0, s 0 is violated, i.e., the variance of disturbance term remains constant though the successive disturbance terms are correlated, then such problem is termed as the problem of autocorrelation. When autocorrelation is present, some or all off-diagonal elements in E(')uu are nonzero. Sometimes the study and explanatory variables have a natural sequence order over time, i.e., the data is collected with respect to time. Such data is termed as time-series data. The disturbance terms in time series data are serially correlated. The autocovariance at lag s is defined as sttsEu( , u ); s 0, 1, 2,... At zero lag, we have constant variance, i.e., 22 0 Eu()t . The autocorrelation coefficient at lag s is defined as Euu()tts s s ;s 0,1,2,... Var() utts Var ( u ) 0 Assume s and s are symmetrical in s , i.e., these coefficients are constant over time and depend only on the length of lag s . The autocorrelation between the successive terms (and)uu21, (and),....uu32 (and)uunn1 gives the autocorrelation of order one, i.e., 1 .