DOCSLIB.ORG

Chapter 11 Autocorrelation

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter 11 Autocorrelation Chapter 11 Autocorrelation One of the basic assumptions in the linear regression model is that the random error components or disturbances are identically and independently distributed. So in the model y Xu , it is assumed that 2 u ifs 0 Eu(,tts u ) 0 if0s i.e., the correlation between the successive disturbances is zero. 2 In this assumption, when Eu(,tts u ) u , s 0 is violated, i.e., the variance of disturbance term does not remain constant, then the problem of heteroskedasticity arises. When Eu(,tts u ) 0, s 0 is violated, i.e., the variance of disturbance term remains constant though the successive disturbance terms are correlated, then such problem is termed as the problem of autocorrelation. When autocorrelation is present, some or all off-diagonal elements in E(')uu are nonzero. Sometimes the study and explanatory variables have a natural sequence order over time, i.e., the data is collected with respect to time. Such data is termed as time-series data. The disturbance terms in time series data are serially correlated. The autocovariance at lag s is defined as sttsEu( , u ); s 0, 1, 2,... At zero lag, we have constant variance, i.e., 22 0 Eu()t . The autocorrelation coefficient at lag s is defined as Euu()tts s s ;s 0,1,2,... Var() utts Var ( u ) 0 Assume s and s are symmetrical in s , i.e., these coefficients are constant over time and depend only on the length of lag s . The autocorrelation between the successive terms (and)uu21, (and),....uu32 (and)uunn1 gives the autocorrelation of order one, i.e., 1 . Similarly, the autocorrelation between the successive terms (uuuuuu3142 and ),( and )...(nn and 2 ) provides the autocorrelation with of order two, i.e., 2 . Regression Analysis | Chapter 11 | Autocorrelation | Shalabh, IIT Kanpur 1 Source of autocorrelation Some of the possible reasons for the introduction of autocorrelation in the data are as follows: 1. Carryover of effect, at least in part, is an important source of autocorrelation. For example, the monthly data on expenditure on the household is influenced by the expenditure of the preceding month. The autocorrelation is present in cross-section data as well as time-series data. In the cross- section data, the neighbouring units tend to be similar with respect to the characteristic under study. In time-series data, time is the factor that produces autocorrelation. Whenever some ordering of sampling units is present, the autocorrelation may arise. 2. Another source of autocorrelation is the effect of deletion of some variables. In regression modeling, it is not possible to include all the variables in the model. There can be various reasons for this, e.g., some variable may be qualitative, sometimes direct observations may not be available on the variable etc. The joint effect of such deleted variables gives rise to autocorrelation in the data. 3. The misspecification of the form of relationship can also introduce autocorrelation in the data. It is assumed that the form of relationship between study and explanatory variables is linear. If there are log or exponential terms present in the model so that the linearity of the model is questionable, then this also gives rise to autocorrelation in the data. 4. The difference between the observed and true values of the variable is called measurement error or errors–in-variable. The presence of measurement errors on the dependent variable may also introduce the autocorrelation in the data. Regression Analysis | Chapter 11 | Autocorrelation | Shalabh, IIT Kanpur 2 Structure of disturbance term: Consider the situation where the disturbances are autocorrelated, 01 n 1 E(') 10n 2 nn12 0 1 11 n 1 12n 0 nn12 1 1 11 n 1 2 12n . u nn12 1 2 Observe that now there are ()nk parameters- 12, ,...,ku , , 12 , ,..., n 1 . These ()nk parameters are to be estimated on the basis of available n observations. Since the number of parameters are more than the number of observations, so the situation is not good from the statistical point of view. In order to handle the situation, some special form and the structure of the disturbance term is needed to be assumed so that the number of parameters in the covariance matrix of disturbance term can be reduced. The following structures are popular in autocorrelation: 1. Autoregressive (AR) process. 2. Moving average (MA) process. 3. Joint autoregression moving average (ARMA) process. Estimation under the first order autoregressive process: Consider a simple linear regression model yXutnttt01 ,1,2,...,. Assume usi ' follow a first-order autoregressive scheme defined as uuttt 1 where 1,E (t ) 0, Regression Analysis | Chapter 11 | Autocorrelation | Shalabh, IIT Kanpur 3 2 ifs 0 E(,tts ) 0if0s for all tn1,2,..., where is the first-order autocorrelation between ut and utt1,1,2,...,. n Now uuttt 1 ()utt21 t 2 tt12 t ... r tr r0 Eu()t 0 222242 Eu(tt ) E ( ) E ( t12 ) E ( t ) ... 24 2' (1 ....) (t s are seriallyindependent) 2 Eu()22 forall. i tu1 2 Euu( ) E22 ... ... tt112123 t t t t t t E ttt 12 ... tt 12 ... E ... 2 tt12 2 u . Similarly, 22 Euu()tt2 u . In general, s 2 Euu()tts u 1 21 n 1 n2 . Euu(') 2 231 n u nn123 n 1 Note that the distribution terms are no more independent and E(')uu 2 I . The disturbance are nonspherical. Regression Analysis | Chapter 11 | Autocorrelation | Shalabh, IIT Kanpur 4 Consequences of autocorrelated disturbances: Consider the model with first-order autoregressive disturbances yX u n1 nk k1 n1 uuttt1 ,1,2,..., t n with assumptions Eu() 0,( Euu ') 2 ifs 0 EE()ttts 0,( ) 0ifs 0 where is a positive definite matrix. The ordinary least squares estimator of is bXXXy (')1 ' (')X XXXu1 '( ) bXXXu (')1 ' Eb()0. So OLSE remains unbiased under autocorrelated disturbances. The covariance matrix of b is Vb()()()' Eb b (')X XXEuuXXX11 '(')(') (')XXXXXX11 ' (') 21 u (').XX The residual vector is e y Xb Hy Hu ee'' yHy uHu ' 1 E(')ee Euu (') E u '(') X X X X ' u 21 ntrXXXX u (') ' . ee' Since s2 , so n 1 2 1 E()strXXXX21u (') ' , nn11 so s2 is a biased estimator of 2 . In fact, s2 has a downward bias. Regression Analysis | Chapter 11 | Autocorrelation | Shalabh, IIT Kanpur 5 Application of OLS fails in case of autocorrelation in the data and leads to serious consequences as an overly optimistic view from R2. narrow confidence interval. usual t -ratio and F ratio tests provide misleading results. the prediction may have large variances. Since disturbances are nonspherical, so generalized least squares estimate of yields more efficient estimates than OLSE. The GLSE of is ˆ ('X 11XX ) ' 1 y E()ˆ ˆ 211 VXX()u ( ' ). The GLSE is best linear unbiased estimator of . Durbin Watson test: The Durbin-Watson (D-W) test is used for testing the hypothesis of lack of the first-order autocorrelation in the disturbance term. The null hypothesis is H0 :0 Use OLS to estimate in y Xu and obtain the residual vector eyXbHy where bXXXyHIXXXX(')11 ', (') '. The D-W test statistic is n 2 eett 1 t2 d n 2 et t1 nn n 2 eett11 ee tt tt22 t 2 nn 2. n 22 2 eett e t tt11 t 1 Regression Analysis | Chapter 11 | Autocorrelation | Shalabh, IIT Kanpur 6 For large n, dr112 dr 2(1 ) where r is the sample autocorrelation coefficient from residuals based on OLSE and can be regarded as the regression coefficient of et on et1 . Here positive autocorrelation of et ’s d 2 negative autocorrelation of et ’s d 2 zero autocorrelation of et ’s d 2 As 11,r so if 1rd 0, then 2 4 and if 0rd 1, then 0 2. So d lies between 0 and 4. Since e depends on X , so for different data sets, different values of d are obtained. So the sampling distribution of d depends on X . Consequently, exact critical values of d cannot be tabulated owing to their dependence on X. Durbin and Watson, therefore, obtained two statistics d and d such that ddd and their sampling distributions do not depend upon X. Considering the distribution of d and d , they tabulated the critical values as dL and dU respectively. They prepared the tables of critical values for 15 nk 100 and 5. Now tables are available for 6n 200 and k 10. The test procedure is as follows: H0 :0 Nature of H1 Reject H0 when Retain H0 when The test is inconclusive when H1 :0 dd L dd U dddL U H1 :0 dd(4L ) dd (4 U ) (4)ddUL (4) d H1 :0 dd L or ddUU (4 d ) dddLU dd(4L ) or (4ddUL ) (4 d ) Values of dL and dU are obtained from tables. Regression Analysis | Chapter 11 | Autocorrelation | Shalabh, IIT Kanpur 7 Limitations of D-W test 1. If d falls in the inconclusive zone, then no conclusive inference can be drawn. This zone becomes fairly larger for low degrees of freedom. One solution is to reject H0 if the test is inconclusive. A better solution is to modify the test as Reject H0 when dd U . Accept H0 when dd U . This test gives a satisfactory solution when values of xi ’s change slowly, e.g., price, expenditure etc. 2. The D-W test is not applicable when the intercept term is absent in the model. In such a case, one can use another critical value, say dM in place of dL . The tables for critical values dM are available. 3. The test is not valid when lagged dependent variables appear as explanatory variables.
Load more

Recommended publications
  • Power Comparisons of Five Most Commonly Used Autocorrelation Tests
    Pak.j.stat.oper.res. Vol.16 No. 1 2020 pp119-130 DOI: http://dx.doi.org/10.18187/pjsor.v16i1.2691 Pakistan Journal of Statistics and Operation Research Power Comparisons of Five Most Commonly Used Autocorrelation Tests Stanislaus S. Uyanto School of Economics and Business, Atma Jaya Catholic University of Indonesia, [email protected] Abstract In regression analysis, autocorrelation of the error terms violates the ordinary least squares assumption that the error terms are uncorrelated. The consequence is that the estimates of coefficients and their standard errors will be wrong if the autocorrelation is ignored. There are many tests for autocorrelation, we want to know which test is more powerful. We use Monte Carlo methods to compare the power of five most commonly used tests for autocorrelation, namely Durbin-Watson, Breusch-Godfrey, Box–Pierce, Ljung Box, and Runs tests in two different linear regression models. The results indicate the Durbin-Watson test performs better in the regression model without lagged dependent variable, although the advantage over the other tests reduce with increasing autocorrelation and sample sizes. For the model with lagged dependent variable, the Breusch-Godfrey test is generally superior to the other tests. Key Words: Correlated error terms; Ordinary least squares assumption; Residuals; Regression diagnostic; Lagged dependent variable. Mathematical Subject Classification: 62J05; 62J20. 1. Introduction An important assumption of the classical linear regression model states that there is no autocorrelation in the error terms. Autocorrelation of the error terms violates the ordinary least squares assumption that the error terms are uncorrelated, meaning that the Gauss Markov theorem (Plackett, 1949, 1950; Greene, 2018) does not apply, and that ordinary least squares estimators are no longer the best linear unbiased estimators.
    [Show full text]
  • Understanding Linear and Logistic Regression Analyses
    EDUCATION • ÉDUCATION METHODOLOGY Understanding linear and logistic regression analyses Andrew Worster, MD, MSc;*† Jerome Fan, MD;* Afisi Ismaila, MSc† SEE RELATED ARTICLE PAGE 105 egression analysis, also termed regression modeling, come). For example, a researcher could evaluate the poten- Ris an increasingly common statistical method used to tial for injury severity score (ISS) to predict ED length-of- describe and quantify the relation between a clinical out- stay by first producing a scatter plot of ISS graphed against come of interest and one or more other variables. In this ED length-of-stay to determine whether an apparent linear issue of CJEM, Cummings and Mayes used linear and lo- relation exists, and then by deriving the best fit straight line gistic regression to determine whether the type of trauma for the data set using linear regression carried out by statis- team leader (TTL) impacts emergency department (ED) tical software. The mathematical formula for this relation length-of-stay or survival.1 The purpose of this educa- would be: ED length-of-stay = k(ISS) + c. In this equation, tional primer is to provide an easily understood overview k (the slope of the line) indicates the factor by which of these methods of statistical analysis. We hope that this length-of-stay changes as ISS changes and c (the “con- primer will not only help readers interpret the Cummings stant”) is the value of length-of-stay when ISS equals zero and Mayes study, but also other research that uses similar and crosses the vertical axis.2 In this hypothetical scenario, methodology.
    [Show full text]
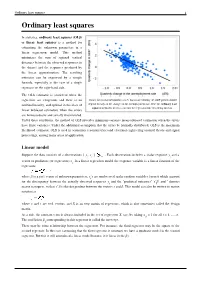
  • Ordinary Least Squares 1 Ordinary Least Squares
    Ordinary least squares 1 Ordinary least squares In statistics, ordinary least squares (OLS) or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear approximation. The resulting estimator can be expressed by a simple formula, especially in the case of a single regressor on the right-hand side. The OLS estimator is consistent when the regressors are exogenous and there is no Okun's law in macroeconomics states that in an economy the GDP growth should multicollinearity, and optimal in the class of depend linearly on the changes in the unemployment rate. Here the ordinary least squares method is used to construct the regression line describing this law. linear unbiased estimators when the errors are homoscedastic and serially uncorrelated. Under these conditions, the method of OLS provides minimum-variance mean-unbiased estimation when the errors have finite variances. Under the additional assumption that the errors be normally distributed, OLS is the maximum likelihood estimator. OLS is used in economics (econometrics) and electrical engineering (control theory and signal processing), among many areas of application. Linear model Suppose the data consists of n observations { y , x } . Each observation includes a scalar response y and a i i i vector of predictors (or regressors) x . In a linear regression model the response variable is a linear function of the i regressors: where β is a p×1 vector of unknown parameters; ε 's are unobserved scalar random variables (errors) which account i for the discrepancy between the actually observed responses y and the "predicted outcomes" x′ β; and ′ denotes i i matrix transpose, so that x′ β is the dot product between the vectors x and β.
    [Show full text]
  • LECTURES 2 - 3 : Stochastic Processes, Autocorrelation Function
    LECTURES 2 - 3 : Stochastic Processes, Autocorrelation function. Stationarity. Important points of Lecture 1: A time series fXtg is a series of observations taken sequentially over time: xt is an observation recorded at a specific time t. Characteristics of times series data: observations are dependent, become available at equally spaced time points and are time-ordered. This is a discrete time series. The purposes of time series analysis are to model and to predict or forecast future values of a series based on the history of that series. 2.2 Some descriptive techniques. (Based on [BD] x1.3 and x1.4) ......................................................................................... Take a step backwards: how do we describe a r.v. or a random vector? ² for a r.v. X: 2 d.f. FX (x) := P (X · x), mean ¹ = EX and variance σ = V ar(X). ² for a r.vector (X1;X2): joint d.f. FX1;X2 (x1; x2) := P (X1 · x1;X2 · x2), marginal d.f.FX1 (x1) := P (X1 · x1) ´ FX1;X2 (x1; 1) 2 2 mean vector (¹1; ¹2) = (EX1; EX2), variances σ1 = V ar(X1); σ2 = V ar(X2), and covariance Cov(X1;X2) = E(X1 ¡ ¹1)(X2 ¡ ¹2) ´ E(X1X2) ¡ ¹1¹2. Often we use correlation = normalized covariance: Cor(X1;X2) = Cov(X1;X2)=fσ1σ2g ......................................................................................... To describe a process X1;X2;::: we define (i) Def. Distribution function: (fi-di) d.f. Ft1:::tn (x1; : : : ; xn) = P (Xt1 · x1;:::;Xtn · xn); i.e. this is the joint d.f. for the vector (Xt1 ;:::;Xtn ). (ii) First- and Second-order moments. ² Mean: ¹X (t) = EXt 2 2 2 2 ² Variance: σX (t) = E(Xt ¡ ¹X (t)) ´ EXt ¡ ¹X (t) 1 ² Autocovariance function: γX (t; s) = Cov(Xt;Xs) = E[(Xt ¡ ¹X (t))(Xs ¡ ¹X (s))] ´ E(XtXs) ¡ ¹X (t)¹X (s) (Note: this is an infinite matrix).
    [Show full text]
  • Alternative Tests for Time Series Dependence Based on Autocorrelation Coefficients
    Alternative Tests for Time Series Dependence Based on Autocorrelation Coefficients Richard M. Levich and Rosario C. Rizzo * Current Draft: December 1998 Abstract: When autocorrelation is small, existing statistical techniques may not be powerful enough to reject the hypothesis that a series is free of autocorrelation. We propose two new and simple statistical tests (RHO and PHI) based on the unweighted sum of autocorrelation and partial autocorrelation coefficients. We analyze a set of simulated data to show the higher power of RHO and PHI in comparison to conventional tests for autocorrelation, especially in the presence of small but persistent autocorrelation. We show an application of our tests to data on currency futures to demonstrate their practical use. Finally, we indicate how our methodology could be used for a new class of time series models (the Generalized Autoregressive, or GAR models) that take into account the presence of small but persistent autocorrelation. _______________________________________________________________ An earlier version of this paper was presented at the Symposium on Global Integration and Competition, sponsored by the Center for Japan-U.S. Business and Economic Studies, Stern School of Business, New York University, March 27-28, 1997. We thank Paul Samuelson and the other participants at that conference for useful comments. * Stern School of Business, New York University and Research Department, Bank of Italy, respectively. 1 1. Introduction Economic time series are often characterized by positive
    [Show full text]
  • 3 Autocorrelation
    3 Autocorrelation Autocorrelation refers to the correlation of a time series with its own past and future values. Autocorrelation is also sometimes called “lagged correlation” or “serial correlation”, which refers to the correlation between members of a series of numbers arranged in time. Positive autocorrelation might be considered a specific form of “persistence”, a tendency for a system to remain in the same state from one observation to the next. For example, the likelihood of tomorrow being rainy is greater if today is rainy than if today is dry. Geophysical time series are frequently autocorrelated because of inertia or carryover processes in the physical system. For example, the slowly evolving and moving low pressure systems in the atmosphere might impart persistence to daily rainfall. Or the slow drainage of groundwater reserves might impart correlation to successive annual flows of a river. Or stored photosynthates might impart correlation to successive annual values of tree-ring indices. Autocorrelation complicates the application of statistical tests by reducing the effective sample size. Autocorrelation can also complicate the identification of significant covariance or correlation between time series (e.g., precipitation with a tree-ring series). Autocorrelation implies that a time series is predictable, probabilistically, as future values are correlated with current and past values. Three tools for assessing the autocorrelation of a time series are (1) the time series plot, (2) the lagged scatterplot, and (3) the autocorrelation function. 3.1 Time series plot Positively autocorrelated series are sometimes referred to as persistent because positive departures from the mean tend to be followed by positive depatures from the mean, and negative departures from the mean tend to be followed by negative departures (Figure 3.1).
    [Show full text]
  • Spatial Autocorrelation: Covariance and Semivariance Semivariance
    Spatial Autocorrelation: Covariance and Semivariancence Lily Housese ­P eters GEOG 593 November 10, 2009 Quantitative Terrain Descriptorsrs Covariance and Semivariogram areare numericc methods used to describe the character of the terrain (ex. Terrain roughness, irregularity) Terrain character has important implications for: 1. the type of sampling strategy chosen 2. estimating DTM accuracy (after sampling and reconstruction) Spatial Autocorrelationon The First Law of Geography ““ Everything is related to everything else, but near things are moo re related than distant things.” (Waldo Tobler) The value of a variable at one point in space is related to the value of that same variable in a nearby location Ex. Moranan ’s I, Gearyary ’s C, LISA Positive Spatial Autocorrelation (Neighbors are similar) Negative Spatial Autocorrelation (Neighbors are dissimilar) R(d) = correlation coefficient of all the points with horizontal interval (d) Covariance The degree of similarity between pairs of surface points The value of similarity is an indicator of the complexity of the terrain surface Smaller the similarity = more complex the terrain surface V = Variance calculated from all N points Cov (d) = Covariance of all points with horizontal interval d Z i = Height of point i M = average height of all points Z i+d = elevation of the point with an interval of d from i Semivariancee Expresses the degree of relationship between points on a surface Equal to half the variance of the differences between all possible points spaced a constant distance apart
    [Show full text]
  • Ordinary Least Squares: the Univariate Case
    Introduction The OLS method The linear causal model A simulation & applications Conclusion and exercises Ordinary Least Squares: the univariate case Clément de Chaisemartin Majeure Economie September 2011 Clément de Chaisemartin Ordinary Least Squares Introduction The OLS method The linear causal model A simulation & applications Conclusion and exercises 1 Introduction 2 The OLS method Objective and principles of OLS Deriving the OLS estimates Do OLS keep their promises ? 3 The linear causal model Assumptions Identification and estimation Limits 4 A simulation & applications OLS do not always yield good estimates... But things can be improved... Empirical applications 5 Conclusion and exercises Clément de Chaisemartin Ordinary Least Squares Introduction The OLS method The linear causal model A simulation & applications Conclusion and exercises Objectives Objective 1 : to make the best possible guess on a variable Y based on X . Find a function of X which yields good predictions for Y . Given cigarette prices, what will be cigarettes sales in September 2010 in France ? Objective 2 : to determine the causal mechanism by which X influences Y . Cetebus paribus type of analysis. Everything else being equal, how a change in X affects Y ? By how much one more year of education increases an individual’s wage ? By how much the hiring of 1 000 more policemen would decrease the crime rate in Paris ? The tool we use = a data set, in which we have the wages and number of years of education of N individuals. Clément de Chaisemartin Ordinary Least Squares Introduction The OLS method The linear causal model A simulation & applications Conclusion and exercises Objective and principles of OLS What we have and what we want For each individual in our data set we observe his wage and his number of years of education.
    [Show full text]
  • Modeling and Generating Multivariate Time Series with Arbitrary Marginals Using a Vector Autoregressive Technique
    Modeling and Generating Multivariate Time Series with Arbitrary Marginals Using a Vector Autoregressive Technique Bahar Deler Barry L. Nelson Dept. of IE & MS, Northwestern University September 2000 Abstract We present a model for representing stationary multivariate time series with arbitrary mar- ginal distributions and autocorrelation structures and describe how to generate data quickly and accurately to drive computer simulations. The central idea is to transform a Gaussian vector autoregressive process into the desired multivariate time-series input process that we presume as having a VARTA (Vector-Autoregressive-To-Anything) distribution. We manipulate the correlation structure of the Gaussian vector autoregressive process so that we achieve the desired correlation structure for the simulation input process. For the purpose of computational efficiency, we provide a numerical method, which incorporates a numerical-search procedure and a numerical-integration technique, for solving this correlation-matching problem. Keywords: Computer simulation, vector autoregressive process, vector time series, multivariate input mod- eling, numerical integration. 1 1 Introduction Representing the uncertainty or randomness in a simulated system by an input model is one of the challenging problems in the practical application of computer simulation. There are an abundance of examples, from manufacturing to service applications, where input modeling is critical; e.g., modeling the time to failure for a machining process, the demand per unit time for inventory of a product, or the times between arrivals of calls to a call center. Further, building a large- scale discrete-event stochastic simulation model may require the development of a large number of, possibly multivariate, input models. Development of these models is facilitated by accurate and automated (or nearly automated) input modeling support.
    [Show full text]
  • Simple Linear Regression with Least Square Estimation: an Overview
    Aditya N More et al, / (IJCSIT) International Journal of Computer Science and Information Technologies, Vol. 7 (6) , 2016, 2394-2396 Simple Linear Regression with Least Square Estimation: An Overview Aditya N More#1, Puneet S Kohli*2, Kshitija H Kulkarni#3 #1-2Information Technology Department,#3 Electronics and Communication Department College of Engineering Pune Shivajinagar, Pune – 411005, Maharashtra, India Abstract— Linear Regression involves modelling a relationship amongst dependent and independent variables in the form of a (2.1) linear equation. Least Square Estimation is a method to determine the constants in a Linear model in the most accurate way without much complexity of solving. Metrics where such as Coefficient of Determination and Mean Square Error is the ith value of the sample data point determine how good the estimation is. Statistical Packages is the ith value of y on the predicted regression such as R and Microsoft Excel have built in tools to perform Least Square Estimation over a given data set. line The above equation can be geometrically depicted by Keywords— Linear Regression, Machine Learning, Least Squares Estimation, R programming figure 2.1. If we draw a square at each point whose length is equal to the absolute difference between the sample data point and the predicted value as shown, each of the square would then represent the residual error in placing the I. INTRODUCTION regression line. The aim of the least square method would Linear Regression involves establishing linear be to place the regression line so as to minimize the sum of relationships between dependent and independent variables.
    [Show full text]
  • Chapter 2: Ordinary Least Squares Regression
    Chapter 2: Ordinary Least Squares In this chapter: 1. Running a simple regression for weight/height example (UE 2.1.4) 2. Contents of the EViews equation window 3. Creating a workfile for the demand for beef example (UE, Table 2.2, p. 45) 4. Importing data from a spreadsheet file named Beef 2.xls 5. Using EViews to estimate a multiple regression model of beef demand (UE 2.2.3) 6. Exercises Ordinary Least Squares (OLS) regression is the core of econometric analysis. While it is important to calculate estimated regression coefficients without the aid of a regression program one time in order to better understand how OLS works (see UE, Table 2.1, p.41), easy access to regression programs makes it unnecessary for everyday analysis.1 In this chapter, we will estimate simple and multivariate regression models in order to pinpoint where the regression statistics discussed throughout the text are found in the EViews program output. Begin by opening the EViews program and opening the workfile named htwt1.wf1 (this is the file of student height and weight that was created and saved in Chapter 1). Running a simple regression for weight/height example (UE 2.1.4): Regression estimation in EViews is performed using the equation object. To create an equation object in EViews, follow these steps: Step 1. Open the EViews workfile named htwt1.wf1 by selecting File/Open/Workfile on the main menu bar and click on the file name. Step 2. Select Objects/New Object/Equation from the workfile menu.2 Step 3.
    [Show full text]
  • Application of General Linear Models (GLM) to Assess Nodule Abundance Based on a Photographic Survey (Case Study from IOM Area, Pacific Ocean)
    minerals Article Application of General Linear Models (GLM) to Assess Nodule Abundance Based on a Photographic Survey (Case Study from IOM Area, Pacific Ocean) Monika Wasilewska-Błaszczyk * and Jacek Mucha Department of Geology of Mineral Deposits and Mining Geology, Faculty of Geology, Geophysics and Environmental Protection, AGH University of Science and Technology, 30-059 Cracow, Poland; [email protected] * Correspondence: [email protected] Abstract: The success of the future exploitation of the Pacific polymetallic nodule deposits depends on an accurate estimation of their resources, especially in small batches, scheduled for extraction in the short term. The estimation based only on the results of direct seafloor sampling using box corers is burdened with a large error due to the long sampling interval and high variability of the nodule abundance. Therefore, estimations should take into account the results of bottom photograph analyses performed systematically and in large numbers along the course of a research vessel. For photographs taken at the direct sampling sites, the relationship linking the nodule abundance with the independent variables (the percentage of seafloor nodule coverage, the genetic types of nodules in the context of their fraction distribution, and the degree of sediment coverage of nodules) was determined using the general linear model (GLM). Compared to the estimates obtained with a simple Citation: Wasilewska-Błaszczyk, M.; linear model linking this parameter only with the seafloor nodule coverage, a significant decrease Mucha, J. Application of General in the standard prediction error, from 4.2 to 2.5 kg/m2, was found. The use of the GLM for the Linear Models (GLM) to Assess assessment of nodule abundance in individual sites covered by bottom photographs, outside of Nodule Abundance Based on a direct sampling sites, should contribute to a significant increase in the accuracy of the estimation of Photographic Survey (Case Study nodule resources.
    [Show full text]