DOCSLIB.ORG

Chapter 2 Simple Linear Regression Analysis the Simple

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter 2 Simple Linear Regression Analysis the Simple Chapter 2 Simple Linear Regression Analysis The simple linear regression model We consider the modelling between the dependent and one independent variable. When there is only one independent variable in the linear regression model, the model is generally termed as a simple linear regression model. When there are more than one independent variables in the model, then the linear model is termed as the multiple linear regression model. The linear model Consider a simple linear regression model yX01 where y is termed as the dependent or study variable and X is termed as the independent or explanatory variable. The terms 0 and 1 are the parameters of the model. The parameter 0 is termed as an intercept term, and the parameter 1 is termed as the slope parameter. These parameters are usually called as regression coefficients. The unobservable error component accounts for the failure of data to lie on the straight line and represents the difference between the true and observed realization of y . There can be several reasons for such difference, e.g., the effect of all deleted variables in the model, variables may be qualitative, inherent randomness in the observations etc. We assume that is observed as independent and identically distributed random variable with mean zero and constant variance 2 . Later, we will additionally assume that is normally distributed. The independent variables are viewed as controlled by the experimenter, so it is considered as non-stochastic whereas y is viewed as a random variable with Ey()01 X and Var() y 2 . Sometimes X can also be a random variable. In such a case, instead of the sample mean and sample variance of y , we consider the conditional mean of y given X x as E(|)yx01 x Regression Analysis | Chapter 2 | Simple Linear Regression Analysis | Shalabh, IIT Kanpur 1 and the conditional variance of y given Xx as Var(|) y x 2 . 2 When the values of 01,and are known, the model is completely described. The parameters 01, and 2 are generally unknown in practice and is unobserved. The determination of the statistical model 2 yX01 depends on the determination (i.e., estimation ) of 01, and . In order to know the values of these parameters, n pairs of observations (xii ,yi )( 1,..., n ) on ( Xy , ) are observed/collected and are used to determine these unknown parameters. Various methods of estimation can be used to determine the estimates of the parameters. Among them, the methods of least squares and maximum likelihood are the popular methods of estimation. Least squares estimation Suppose a sample of n sets of paired observations (xii ,yi ) ( 1,2,..., n ) is available. These observations are assumed to satisfy the simple linear regression model, and so we can write yxiniii01 (1,2,...,). The principle of least squares estimates the parameters 01and by minimizing the sum of squares of the difference between the observations and the line in the scatter diagram. Such an idea is viewed from different perspectives. When the vertical difference between the observations and the line in the scatter diagram is considered, and its sum of squares is minimized to obtain the estimates of 01and , the method is known as direct regression. yi (xi, Y 01 X (X , i xi Direct regression Regression Analysis | Chapter 2 | Simple Linear Regression Analysis | Shalabh, IIT Kanpur 2 Alternatively, the sum of squares of the difference between the observations and the line in the horizontal direction in the scatter diagram can be minimized to obtain the estimates of 01and . This is known as a reverse (or inverse) regression method. yi YX 01 (xi, yi) (Xi, Yi) xi, Reverse regression method Instead of horizontal or vertical errors, if the sum of squares of perpendicular distances between the observations and the line in the scatter diagram is minimized to obtain the estimates of 01and , the method is known as orthogonal regression or major axis regression method. yi (xi YX 01 (Xi ) xi Major axis regression method Regression Analysis | Chapter 2 | Simple Linear Regression Analysis | Shalabh, IIT Kanpur 3 Instead of minimizing the distance, the area can also be minimized. The reduced major axis regression method minimizes the sum of the areas of rectangles defined between the observed data points and the nearest point on the line in the scatter diagram to obtain the estimates of regression coefficients. This is shown in the following figure: yi (xi yi) YX 01 (Xi, Yi) xi Reduced major axis method The method of least absolute deviation regression considers the sum of the absolute deviation of the observations from the line in the vertical direction in the scatter diagram as in the case of direct regression to obtain the estimates of 01and . No assumption is required about the form of the probability distribution of i in deriving the least squares estimates. For the purpose of deriving the statistical inferences only, we assume that i 's are random 2 variable with E()ii 0,()Var and Cov (, ij )0forall i j(, i j 1,2,...,). n This assumption is needed to find the mean, variance and other properties of the least-squares estimates. The assumption that i 's are normally distributed is utilized while constructing the tests of hypotheses and confidence intervals of the parameters. Based on these approaches, different estimates of 01and are obtained which have different statistical properties. Among them, the direct regression approach is more popular. Generally, the direct regression estimates are referred to as the least-squares estimates or ordinary least squares estimates. Regression Analysis | Chapter 2 | Simple Linear Regression Analysis | Shalabh, IIT Kanpur 4 Direct regression method This method is also known as the ordinary least squares estimation. Assuming that a set of n paired observations on (xii ,yi ), 1,2,..., n are available which satisfy the linear regression model yX01 . So we can write the model for each observation as yxiii 01, (in 1,2,..., ) . The direct regression approach minimizes the sum of squares nn 22 S(,)01 ii (y 0 1x i ) ii11 with respect to 01and . The partial derivatives of S(,)01 with respect to 0 is n S(,)01 2( yxti 01 ) 0 i1 and the partial derivative of S(,)01 with respect to 1 is n S(,)01 2( yxxiii 01 ). 1 i1 The solutions of 01and are obtained by setting S(,) 01 0 0 S(,) 01 0. 1 The solutions of these two equations are called the direct regression estimators, or usually called as the ordinary least squares (OLS) estimators of 01and . This gives the ordinary least squares estimates bb0011of and of as bybx01 sxy b1 sxx where nnnn 2 11 sxy()(),(),xxyy i i s xx xx i x xy i , y i . iiii1111nn Regression Analysis | Chapter 2 | Simple Linear Regression Analysis | Shalabh, IIT Kanpur 5 Further, we have 2S(,) n 012(1)2, n 2 0 i1 2S(,) n 01 2 x2 2 i 1 i1 2 n S(,)01 22. xt nx 01 i1 The Hessian matrix which is the matrix of second-order partial derivatives, in this case, is given as 22 SS(,)01 (,) 01 2 H* 001 22SS(,) (,) 01 01 2 01 1 nnx 2n 2 nx xi i1 ' 2, x x ' where (1,1,...,1)' is a n -vector of elements unity and x (xx1 ,...,n )' is a n -vector of observations on X . The matrix H * is positive definite if its determinant and the element in the first row and column of H * are positive. The determinant of H * is given by n 222 H *4nxnx i i1 n 2 4(nxx i ) i1 0. n 2 The case when ()0xxi is not interesting because all the observations, in this case, are identical, i.e. i1 xi c (some constant). In such a case, there is no relationship between x and y in the context of regression n 2 analysis. Since ()0,xxi therefore H 0. So H is positive definite for any (,)01 , therefore, i1 S(,)01 has a global minimum at (,).bb01 Regression Analysis | Chapter 2 | Simple Linear Regression Analysis | Shalabh, IIT Kanpur 6 The fitted line or the fitted linear regression model is yb01 bx. The predicted values are ybbxiˆii01(1,2,...,). n The difference between the observed value yi and the fitted (or predicted) value yˆi is called a residual. The ith residual is defined as eyyiiii~ˆ ( 1,2,..., n ) yyiiˆ ybbxii().01 Properties of the direct regression estimators: Unbiased property: sxy Note that bbybx101and are the linear combinations of yii (1,...,). n sxx Therefore n bky1 ii i1 nn wherekxxsii ( ) / xx . Note that k i 0 and kx ii 1, so ii11 n Eb()1 kEyii () i1 n kxii(01 ) . i1 1. This b1 is an unbiased estimator of 1 . Next Eb()01 E y bx E01xbx 1 01xx 1 0. Thus b0 is an unbiased estimator of 0 . Regression Analysis | Chapter 2 | Simple Linear Regression Analysis | Shalabh, IIT Kanpur 7 Variances: Using the assumption that ysi ' are independently distributed, the variance of b1 is n 2 Var() b1 kii Var () y k ijij k Cov (, y y ) iiji1 2 ()xxi 2 i (Cov ( y , y ) 0 as y ,..., y are independent) s2 ij1 n xx 2 sxx = 2 sxx 2 = . sxx The variance of b0 is 2 Var() b011 Var ()y xVarb ()2 xCov (,).y b First, we find that Cov(, y b111 ) E y E () y b E () b Ecy() ii 1 i 1 Eccxc()(ii01 iiiii ) 1 n iiii i 1 0000 n 0 So 2 2 1 x Var() b0 . nsxx Covariance: The covariance between b0 and b1 is Cov(,) b01 b Cov (,) y b 1 xVar () b 1 x 2.
Load more

Recommended publications
  • A Generalized Linear Model for Principal Component Analysis of Binary Data
    A Generalized Linear Model for Principal Component Analysis of Binary Data Andrew I. Schein Lawrence K. Saul Lyle H. Ungar Department of Computer and Information Science University of Pennsylvania Moore School Building 200 South 33rd Street Philadelphia, PA 19104-6389 {ais,lsaul,ungar}@cis.upenn.edu Abstract they are not generally appropriate for other data types. Recently, Collins et al.[5] derived generalized criteria We investigate a generalized linear model for for dimensionality reduction by appealing to proper- dimensionality reduction of binary data. The ties of distributions in the exponential family. In their model is related to principal component anal- framework, the conventional PCA of real-valued data ysis (PCA) in the same way that logistic re- emerges naturally from assuming a Gaussian distribu- gression is related to linear regression. Thus tion over a set of observations, while generalized ver- we refer to the model as logistic PCA. In this sions of PCA for binary and nonnegative data emerge paper, we derive an alternating least squares respectively by substituting the Bernoulli and Pois- method to estimate the basis vectors and gen- son distributions for the Gaussian. For binary data, eralized linear coefficients of the logistic PCA the generalized model's relationship to PCA is anal- model. The resulting updates have a simple ogous to the relationship between logistic and linear closed form and are guaranteed at each iter- regression[12]. In particular, the model exploits the ation to improve the model's likelihood. We log-odds as the natural parameter of the Bernoulli dis- evaluate the performance of logistic PCA|as tribution and the logistic function as its canonical link.
    [Show full text]
  • Goodness of Fit: What Do We Really Want to Know? I
    PHYSTAT2003, SLAC, Stanford, California, September 8-11, 2003 Goodness of Fit: What Do We Really Want to Know? I. Narsky California Institute of Technology, Pasadena, CA 91125, USA Definitions of the goodness-of-fit problem are discussed. A new method for estimation of the goodness of fit using distance to nearest neighbor is described. Performance of several goodness-of-fit methods is studied for time-dependent CP asymmetry measurements of sin(2β). 1. INTRODUCTION of the test is then defined as the probability of ac- cepting the null hypothesis given it is true, and the The goodness-of-fit problem has recently attracted power of the test, 1 − αII , is defined as the probabil- attention from the particle physics community. In ity of rejecting the null hypothesis given the alterna- modern particle experiments, one often performs an tive is true. Above, αI and αII denote Type I and unbinned likelihood fit to data. The experimenter Type II errors, respectively. An ideal hypothesis test then needs to estimate how accurately the fit function is uniformly most powerful (UMP) because it gives approximates the observed distribution. A number of the highest power among all possible tests at the fixed methods have been used to solve this problem in the confidence level. In most realistic problems, it is not past [1], and a number of methods have been recently possible to find a UMP test and one has to consider proposed [2, 3] in the physics literature. various tests with acceptable power functions. For binned data, one typically applies a χ2 statistic There is a long-standing controversy about the con- to estimate the fit quality.
    [Show full text]
  • A Simple Censored Median Regression Estimator
    Statistica Sinica 16(2006), 1043-1058 A SIMPLE CENSORED MEDIAN REGRESSION ESTIMATOR Lingzhi Zhou The Hong Kong University of Science and Technology Abstract: Ying, Jung and Wei (1995) proposed an estimation procedure for the censored median regression model that regresses the median of the survival time, or its transform, on the covariates. The procedure requires solving complicated nonlinear equations and thus can be very difficult to implement in practice, es- pecially when there are multiple covariates. Moreover, the asymptotic covariance matrix of the estimator involves the density of the errors that cannot be esti- mated reliably. In this paper, we propose a new estimator for the censored median regression model. Our estimation procedure involves solving some convex min- imization problems and can be easily implemented through linear programming (Koenker and D'Orey (1987)). In addition, a resampling method is presented for estimating the covariance matrix of the new estimator. Numerical studies indi- cate the superiority of the finite sample performance of our estimator over that in Ying, Jung and Wei (1995). Key words and phrases: Censoring, convexity, LAD, resampling. 1. Introduction The accelerated failure time (AFT) model, which relates the logarithm of the survival time to covariates, is an attractive alternative to the popular Cox (1972) proportional hazards model due to its ease of interpretation. The model assumes that the failure time T , or some monotonic transformation of it, is linearly related to the covariate vector Z 0 Ti = β0Zi + "i; i = 1; : : : ; n: (1.1) Under censoring, we only observe Yi = min(Ti; Ci), where Ci are censoring times, and Ti and Ci are independent conditional on Zi.
    [Show full text]
  • Understanding Linear and Logistic Regression Analyses
    EDUCATION • ÉDUCATION METHODOLOGY Understanding linear and logistic regression analyses Andrew Worster, MD, MSc;*† Jerome Fan, MD;* Afisi Ismaila, MSc† SEE RELATED ARTICLE PAGE 105 egression analysis, also termed regression modeling, come). For example, a researcher could evaluate the poten- Ris an increasingly common statistical method used to tial for injury severity score (ISS) to predict ED length-of- describe and quantify the relation between a clinical out- stay by first producing a scatter plot of ISS graphed against come of interest and one or more other variables. In this ED length-of-stay to determine whether an apparent linear issue of CJEM, Cummings and Mayes used linear and lo- relation exists, and then by deriving the best fit straight line gistic regression to determine whether the type of trauma for the data set using linear regression carried out by statis- team leader (TTL) impacts emergency department (ED) tical software. The mathematical formula for this relation length-of-stay or survival.1 The purpose of this educa- would be: ED length-of-stay = k(ISS) + c. In this equation, tional primer is to provide an easily understood overview k (the slope of the line) indicates the factor by which of these methods of statistical analysis. We hope that this length-of-stay changes as ISS changes and c (the “con- primer will not only help readers interpret the Cummings stant”) is the value of length-of-stay when ISS equals zero and Mayes study, but also other research that uses similar and crosses the vertical axis.2 In this hypothetical scenario, methodology.
    [Show full text]
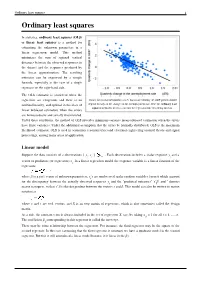
  • Ordinary Least Squares 1 Ordinary Least Squares
    Ordinary least squares 1 Ordinary least squares In statistics, ordinary least squares (OLS) or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear approximation. The resulting estimator can be expressed by a simple formula, especially in the case of a single regressor on the right-hand side. The OLS estimator is consistent when the regressors are exogenous and there is no Okun's law in macroeconomics states that in an economy the GDP growth should multicollinearity, and optimal in the class of depend linearly on the changes in the unemployment rate. Here the ordinary least squares method is used to construct the regression line describing this law. linear unbiased estimators when the errors are homoscedastic and serially uncorrelated. Under these conditions, the method of OLS provides minimum-variance mean-unbiased estimation when the errors have finite variances. Under the additional assumption that the errors be normally distributed, OLS is the maximum likelihood estimator. OLS is used in economics (econometrics) and electrical engineering (control theory and signal processing), among many areas of application. Linear model Suppose the data consists of n observations { y , x } . Each observation includes a scalar response y and a i i i vector of predictors (or regressors) x . In a linear regression model the response variable is a linear function of the i regressors: where β is a p×1 vector of unknown parameters; ε 's are unobserved scalar random variables (errors) which account i for the discrepancy between the actually observed responses y and the "predicted outcomes" x′ β; and ′ denotes i i matrix transpose, so that x′ β is the dot product between the vectors x and β.
    [Show full text]
  • Cluster Analysis, a Powerful Tool for Data Analysis in Education
    International Statistical Institute, 56th Session, 2007: Rita Vasconcelos, Mßrcia Baptista Cluster Analysis, a powerful tool for data analysis in Education Vasconcelos, Rita Universidade da Madeira, Department of Mathematics and Engeneering Caminho da Penteada 9000-390 Funchal, Portugal E-mail: [email protected] Baptista, Márcia Direcção Regional de Saúde Pública Rua das Pretas 9000 Funchal, Portugal E-mail: [email protected] 1. Introduction A database was created after an inquiry to 14-15 - year old students, which was developed with the purpose of identifying the factors that could socially and pedagogically frame the results in Mathematics. The data was collected in eight schools in Funchal (Madeira Island), and we performed a Cluster Analysis as a first multivariate statistical approach to this database. We also developed a logistic regression analysis, as the study was carried out as a contribution to explain the success/failure in Mathematics. As a final step, the responses of both statistical analysis were studied. 2. Cluster Analysis approach The questions that arise when we try to frame socially and pedagogically the results in Mathematics of 14-15 - year old students, are concerned with the types of decisive factors in those results. It is somehow underlying our objectives to classify the students according to the factors understood by us as being decisive in students’ results. This is exactly the aim of Cluster Analysis. The hierarchical solution that can be observed in the dendogram presented in the next page, suggests that we should consider the 3 following clusters, since the distances increase substantially after it: Variables in Cluster1: mother qualifications; father qualifications; student’s results in Mathematics as classified by the school teacher; student’s results in the exam of Mathematics; time spent studying.
    [Show full text]
  • The Detection of Heteroscedasticity in Regression Models for Psychological Data
    Psychological Test and Assessment Modeling, Volume 58, 2016 (4), 567-592 The detection of heteroscedasticity in regression models for psychological data Andreas G. Klein1, Carla Gerhard2, Rebecca D. Büchner2, Stefan Diestel3 & Karin Schermelleh-Engel2 Abstract One assumption of multiple regression analysis is homoscedasticity of errors. Heteroscedasticity, as often found in psychological or behavioral data, may result from misspecification due to overlooked nonlinear predictor terms or to unobserved predictors not included in the model. Although methods exist to test for heteroscedasticity, they require a parametric model for specifying the structure of heteroscedasticity. The aim of this article is to propose a simple measure of heteroscedasticity, which does not need a parametric model and is able to detect omitted nonlinear terms. This measure utilizes the dispersion of the squared regression residuals. Simulation studies show that the measure performs satisfactorily with regard to Type I error rates and power when sample size and effect size are large enough. It outperforms the Breusch-Pagan test when a nonlinear term is omitted in the analysis model. We also demonstrate the performance of the measure using a data set from industrial psychology. Keywords: Heteroscedasticity, Monte Carlo study, regression, interaction effect, quadratic effect 1Correspondence concerning this article should be addressed to: Prof. Dr. Andreas G. Klein, Department of Psychology, Goethe University Frankfurt, Theodor-W.-Adorno-Platz 6, 60629 Frankfurt; email: [email protected] 2Goethe University Frankfurt 3International School of Management Dortmund Leipniz-Research Centre for Working Environment and Human Factors 568 A. G. Klein, C. Gerhard, R. D. Büchner, S. Diestel & K. Schermelleh-Engel Introduction One of the standard assumptions underlying a linear model is that the errors are inde- pendently identically distributed (i.i.d.).
    [Show full text]
  • Ordinary Least Squares: the Univariate Case
    Introduction The OLS method The linear causal model A simulation & applications Conclusion and exercises Ordinary Least Squares: the univariate case Clément de Chaisemartin Majeure Economie September 2011 Clément de Chaisemartin Ordinary Least Squares Introduction The OLS method The linear causal model A simulation & applications Conclusion and exercises 1 Introduction 2 The OLS method Objective and principles of OLS Deriving the OLS estimates Do OLS keep their promises ? 3 The linear causal model Assumptions Identification and estimation Limits 4 A simulation & applications OLS do not always yield good estimates... But things can be improved... Empirical applications 5 Conclusion and exercises Clément de Chaisemartin Ordinary Least Squares Introduction The OLS method The linear causal model A simulation & applications Conclusion and exercises Objectives Objective 1 : to make the best possible guess on a variable Y based on X . Find a function of X which yields good predictions for Y . Given cigarette prices, what will be cigarettes sales in September 2010 in France ? Objective 2 : to determine the causal mechanism by which X influences Y . Cetebus paribus type of analysis. Everything else being equal, how a change in X affects Y ? By how much one more year of education increases an individual’s wage ? By how much the hiring of 1 000 more policemen would decrease the crime rate in Paris ? The tool we use = a data set, in which we have the wages and number of years of education of N individuals. Clément de Chaisemartin Ordinary Least Squares Introduction The OLS method The linear causal model A simulation & applications Conclusion and exercises Objective and principles of OLS What we have and what we want For each individual in our data set we observe his wage and his number of years of education.
    [Show full text]
  • Linear, Ridge Regression, and Principal Component Analysis
    Linear, Ridge Regression, and Principal Component Analysis Linear, Ridge Regression, and Principal Component Analysis Jia Li Department of Statistics The Pennsylvania State University Email: [email protected] http://www.stat.psu.edu/∼jiali Jia Li http://www.stat.psu.edu/∼jiali Linear, Ridge Regression, and Principal Component Analysis Introduction to Regression I Input vector: X = (X1, X2, ..., Xp). I Output Y is real-valued. I Predict Y from X by f (X ) so that the expected loss function E(L(Y , f (X ))) is minimized. I Square loss: L(Y , f (X )) = (Y − f (X ))2 . I The optimal predictor ∗ 2 f (X ) = argminf (X )E(Y − f (X )) = E(Y | X ) . I The function E(Y | X ) is the regression function. Jia Li http://www.stat.psu.edu/∼jiali Linear, Ridge Regression, and Principal Component Analysis Example The number of active physicians in a Standard Metropolitan Statistical Area (SMSA), denoted by Y , is expected to be related to total population (X1, measured in thousands), land area (X2, measured in square miles), and total personal income (X3, measured in millions of dollars). Data are collected for 141 SMSAs, as shown in the following table. i : 1 2 3 ... 139 140 141 X1 9387 7031 7017 ... 233 232 231 X2 1348 4069 3719 ... 1011 813 654 X3 72100 52737 54542 ... 1337 1589 1148 Y 25627 15389 13326 ... 264 371 140 Goal: Predict Y from X1, X2, and X3. Jia Li http://www.stat.psu.edu/∼jiali Linear, Ridge Regression, and Principal Component Analysis Linear Methods I The linear regression model p X f (X ) = β0 + Xj βj .
    [Show full text]
  • Simple Linear Regression with Least Square Estimation: an Overview
    Aditya N More et al, / (IJCSIT) International Journal of Computer Science and Information Technologies, Vol. 7 (6) , 2016, 2394-2396 Simple Linear Regression with Least Square Estimation: An Overview Aditya N More#1, Puneet S Kohli*2, Kshitija H Kulkarni#3 #1-2Information Technology Department,#3 Electronics and Communication Department College of Engineering Pune Shivajinagar, Pune – 411005, Maharashtra, India Abstract— Linear Regression involves modelling a relationship amongst dependent and independent variables in the form of a (2.1) linear equation. Least Square Estimation is a method to determine the constants in a Linear model in the most accurate way without much complexity of solving. Metrics where such as Coefficient of Determination and Mean Square Error is the ith value of the sample data point determine how good the estimation is. Statistical Packages is the ith value of y on the predicted regression such as R and Microsoft Excel have built in tools to perform Least Square Estimation over a given data set. line The above equation can be geometrically depicted by Keywords— Linear Regression, Machine Learning, Least Squares Estimation, R programming figure 2.1. If we draw a square at each point whose length is equal to the absolute difference between the sample data point and the predicted value as shown, each of the square would then represent the residual error in placing the I. INTRODUCTION regression line. The aim of the least square method would Linear Regression involves establishing linear be to place the regression line so as to minimize the sum of relationships between dependent and independent variables.
    [Show full text]
  • Chapter 2: Ordinary Least Squares Regression
    Chapter 2: Ordinary Least Squares In this chapter: 1. Running a simple regression for weight/height example (UE 2.1.4) 2. Contents of the EViews equation window 3. Creating a workfile for the demand for beef example (UE, Table 2.2, p. 45) 4. Importing data from a spreadsheet file named Beef 2.xls 5. Using EViews to estimate a multiple regression model of beef demand (UE 2.2.3) 6. Exercises Ordinary Least Squares (OLS) regression is the core of econometric analysis. While it is important to calculate estimated regression coefficients without the aid of a regression program one time in order to better understand how OLS works (see UE, Table 2.1, p.41), easy access to regression programs makes it unnecessary for everyday analysis.1 In this chapter, we will estimate simple and multivariate regression models in order to pinpoint where the regression statistics discussed throughout the text are found in the EViews program output. Begin by opening the EViews program and opening the workfile named htwt1.wf1 (this is the file of student height and weight that was created and saved in Chapter 1). Running a simple regression for weight/height example (UE 2.1.4): Regression estimation in EViews is performed using the equation object. To create an equation object in EViews, follow these steps: Step 1. Open the EViews workfile named htwt1.wf1 by selecting File/Open/Workfile on the main menu bar and click on the file name. Step 2. Select Objects/New Object/Equation from the workfile menu.2 Step 3.
    [Show full text]
  • Application of General Linear Models (GLM) to Assess Nodule Abundance Based on a Photographic Survey (Case Study from IOM Area, Pacific Ocean)
    minerals Article Application of General Linear Models (GLM) to Assess Nodule Abundance Based on a Photographic Survey (Case Study from IOM Area, Pacific Ocean) Monika Wasilewska-Błaszczyk * and Jacek Mucha Department of Geology of Mineral Deposits and Mining Geology, Faculty of Geology, Geophysics and Environmental Protection, AGH University of Science and Technology, 30-059 Cracow, Poland; [email protected] * Correspondence: [email protected] Abstract: The success of the future exploitation of the Pacific polymetallic nodule deposits depends on an accurate estimation of their resources, especially in small batches, scheduled for extraction in the short term. The estimation based only on the results of direct seafloor sampling using box corers is burdened with a large error due to the long sampling interval and high variability of the nodule abundance. Therefore, estimations should take into account the results of bottom photograph analyses performed systematically and in large numbers along the course of a research vessel. For photographs taken at the direct sampling sites, the relationship linking the nodule abundance with the independent variables (the percentage of seafloor nodule coverage, the genetic types of nodules in the context of their fraction distribution, and the degree of sediment coverage of nodules) was determined using the general linear model (GLM). Compared to the estimates obtained with a simple Citation: Wasilewska-Błaszczyk, M.; linear model linking this parameter only with the seafloor nodule coverage, a significant decrease Mucha, J. Application of General in the standard prediction error, from 4.2 to 2.5 kg/m2, was found. The use of the GLM for the Linear Models (GLM) to Assess assessment of nodule abundance in individual sites covered by bottom photographs, outside of Nodule Abundance Based on a direct sampling sites, should contribute to a significant increase in the accuracy of the estimation of Photographic Survey (Case Study nodule resources.
    [Show full text]