DOCSLIB.ORG

Chemistry 163B Refrigerators and Generalization of Ideal Gas Carnot

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chemistry 163B Refrigerators and Generalization of Ideal Gas Carnot Chemistry 163B Winter 2020 Refrigerators and Generalization of Carnot Cycle statements of the Second Law of Thermodynamics Lecture 10 1. Macroscopic properties of an isolated system eventually assume Chemistry 163B constant values (e.g. pressure in two bulbs of gas becomes constant; two block of metal reach same T) [Andrews. p37] Refrigerators and 2. It is impossible to construct a device that operates in cycles and that converts heat into work without producing some other change Generalization of in the surroundings. Kelvin’s Statement [Raff p 157]; Carnot Cycle 3. It is impossible to have a natural process which produces no other Ideal Gas Carnot effect than absorption of heat from a colder body and discharge of heat to a warmer body. Clausius’s Statement, refrigerator (four steps to exactitude) 4. In the neighborhood of any prescribed initial state there are states which cannot be reached by any adiabatic process E&R pp 125-129, 132-139 Raff pp. 159-164 4th ~ Caratheodory’s statement [Andrews p. 58] E&R3rd pp 86-91, 109-111 1 2 perpetual motion of the first kind (produce work with no heat input) perpetual motion and the 1st and 2nd Laws of thermodynamics Escher “Waterfall” cyclic machines: cyclic machine 1st Law U=0 q=-w =w (water ‘flows downhill’ sys surr to pillar on left; ‘round and ‘round) no energy input nd 2 Law qin > wsurr work on surroundings It is impossible to construct a device that operates in cycles and that converts heat into work without VIOLATES 1st LAW producing some other change in the surroundings. Kelvin’s Statement [Raff p 157]; Carnot Cycle 3 4 perpetual motion of the second kind (produce work extracting heat remember Carnot engine from cooler source to run machine at warmer temperature) Brownian Ratchet • does net work on surroundings BUT • extracts heat from surroundings at TU qU(I) < 0 • gives off heat to surroundings at TL qL(III) > 0 get work only if T1 > T2 https://en.wikipedia.org/wiki/Brownian_ratchet. 5 6 1 Chemistry 163B Winter 2020 Refrigerators and Generalization of Carnot Cycle roadmap for second law goals for lecture[s] 1. Phenomenological statements (what is ALWAYS observed) • Carnot in reverse: refrigerators and heat pumps 2. Ideal gas Carnot [reversible] cycle efficiency of heat → work (Carnot cycle transfers heat only at TU and TL ) • Show that εideal gas rev Carnot εany other machine otherwise one of 3. Any cyclic engine operating between TU and TL must have an the phenomenological statements violated equal or lower efficiency than Carnot OR VIOLATE one of the phenomenological statements (observations) • Not only for ideal gas but εideal gas rev Carnot = εany other rev Carnot 4. Generalize Carnot to any reversible cycle (E&R fig 5.4) 5. Show that for this REVERSIBLE cycle dq dq • dSreversible dS reversible 0 qqUL0 (dq inexact differential) TT but and Sis STATE FUNCTION q q dq UrevL 0( something special about ) TTUL T 6. S, entropy and spontaneous changes 7 8 remember Carnot engine Carnot engine arithmetic (for below table see handout) • does net work on surroundings and • net heat qU(I) + qL(III) = -wtotal 9 10 refrigerators and heat pumps: running the Carnot cycle in REVERSE heat pumps and refrigerators (fig. 5.20 E&R4th) 5.17 ER3rd Figure 5.20 Application • it only makes ‘sense’ to talk about of the principle of a reverse Carnot heat running a process in REVERSE for engine to refrigeration and household heating. (q ) <0 reversible processes (on a PV The reverse Carnot heat revcarnot U engine can be used to diagram there is no ‘reverse’ process induce heat flow from a wrevcarnot>0 cold reservoir to a hot (qrevcarnot)L>0 for irreversible expansion against reservoir with the input w <0 i.e. w of work. The hot surr in constant Pext) reservoir in both (a) and (b) is a room. The cold reservoir can be configured as the inside • however the Carnot cycle is a of a refrigerator or outside ambient air, combination of reversible processes earth, or water for a heat pump refrigerator heat pump 11 12 2 Chemistry 163B Winter 2020 Refrigerators and Generalization of Carnot Cycle Carnot refrigerator arithmetic (just negatives of Carnot engine) reverse Carnot cycle: a refrigerator for below table see handout wsys=-wsurr > 0 qU < 0 heat out at TU work done ON system qL >0 heat in at TL cyclic process IV adiabatic expansion III isothermal expansion q Coefficient of performance surr_ III qTIII L II adiabatic compression C of refrigerator: rR I isothermal compression wwTTtotal total U L 13 eqn 5.69 ER4th 5.45 E&R3rd 14 reverse Carnot cycle: a heat pump “goodness of performance” w =-w > 0 sys surr Since refrigerators and heat pumps are just Carnot machines qU < 0 heat out at TU work done ON system in reverse, the relationship for =-wtotal/qI = (TU-TL)/TU holds for these cycles. However only for “engines” does it represent the efficiency or “goodness of performance” (worktotal out/heat in). For a refrigerator performance is (heatin at TL/worktotal) q from freezer qTIII L C eqn 5.69 ER4th 5.45 E&R3rd rR wwTT total total U L † HW5 #28 (E&R4th P5.33) For a heat pump performance is (heat /work ) qL >0 heat in at TL cyclic process out at TU total IV adiabatic expansion q q T C given off to room I U ( > 1) III isothermal expansion hp HP wwTTtotal total U L II adiabatic compression eqn 5.68 ER4th 5.44 E&R3rd I isothermal compression 15 16 one more important FACTOID about Carnot machine one more important FACTOID about Carnot machine for complete reversible Carnot cycle: P nRT ln 1 dq U P constant TTrev 2 ∮ dU= U = 0? U T I T U ∮ dH= H = 0? dq adibatic rev 0 ∮ dq =q = ?0 T dqrev rev II 0 ∮ dw =w = ?0 ? rev P1 nRTL ln T dq P cycle constant TTrev 2 BUT ALSO LET’S LOOK AT: L T III T L dq adibatic rev 0 T dqrev IV have we uncovered a new state function entropy (S) ?? T dq cycle SdS rev does it just apply T to ideal gas Carnot cycle ??? 17 18 3 Chemistry 163B Winter 2020 Refrigerators and Generalization of Carnot Cycle Generalization of Ideal Gas Carnot Cycle Carnot machine Our work on the (reversible) Carnot Cycle using an ideal 1. gas as the ‘working substance” lead to the relationship Carnot machine: cyclic, reversible, machine exchanging heat with environment at only -wtotal T U - T L == two temperatures TU, TL qTUU However, the second law applies to machines with any ‘working substance’ and general cycles. Carnot engine: ‘forward’ Carnot cycle 2. The following presentation shows that a (reversible) Carnot machine Carnot heat pump: ‘reverse’ Carnot cycle with ‘any working substance’ cannot have rev any ws > carnot ideal gas . 3. REVERSING the directions of the ideal gas and ‘any rev Carnot’ (e.g. Raff, pp 160-162) shows that = T w rev any ws carnot ideal gas 1 L =total applies to both forward and TqUU 4. One can also show (E&R4th Fig 5.15 Fig 5.433rd , Raff 162-164 ) that any Carnot machine has ∮ dqrev /T =0 and that any reversible reverse Carnot cycles machine cycle can be expressed as a sum of Carnot cycles. 19 20 can x > c for any Carnot machine X vs ideal gas Carnot machine C ??? CAN εx> εCarnot : worksheet for numerical example (all wx goes into wCarnot ) (generalizing εrev=1-TL/TU that was derived for reversible ideal gas Carnot cycle) machine X: any ‘working substance” (not necessarily ideal gas) TRY: εx=0.6 > εcarnot =0.5 ; specify heat into x (qu)x=100 J and all (wout)x= (win)carnot exchanges heat at only two temperatures TU and TL x=0.6 +100J (wt)x=-60J -120J nd heat pump engine heat pump engine viol0.6ation of 2 Law 0.5 -40J -60J +60J +60J (qu)C=-120J C=0.5 the machine X operates as a Carnot engine doing work, while the machine C operates as a reverse Carnot ideal gas engine -w wtotal=0 acting as a heat pump. t -w t q=U Clausius In this example the work done by X, (wt)x is totally used by C: ε (q ) = -20J (into T ) ε= U=qUt +qL +w =0 U total u (wt)c = (wt)x q w=-tU q ε U (qL)total=+20J (out of TL) 21 22 for each of the cyclic processes CAN εx> εCarnot : worksheet for numerical example (all wx goes into wCarnot ) Clausius Statement of Second Law (numerical example) TRY: εx=0.6 > εcarnot =0.5 ; specify heat into x (qu)x=100 J and all (wout)x= (win)carnot we assumed an εx > εCig for ideal gas Carnot and calculated wtotal=0 +100J -120J (qL)total=+20J (into ‘combo engine’ out of cold reservoir at Tlower) 0.6 0.5 (qU)total=-20J (out of ‘combo engine’ into heat reservoir at Tupper) -40J -60J +60J +60J BUT: It is impossible to have a natural process which produces no other effect than absorption of heat from a colder body and discharge of heat to a warmer body. Clausius’s Statement -w t wtotal=0 -w t q=U ε= ε U=qUt +qL +w =0 (qU)total= -20J (into Tu) specific example showed: q w=-tU q ε if second law holds > cannot be true U (qL)total=+20J (out of TL) x cig nd 23 for x= any Carnot ideal gas or not 24 for each of the cyclic processes violation of 2 Law 4 Chemistry 163B Winter 2020 Refrigerators and Generalization of Carnot Cycle general proof: can x > c for Carnot machine X vs ideal gas Carnot machine C ??? general proof: can x > c for Carnot machine X vs ideal gas Carnot machine C ??? So (qU)total < 0 and (qL)total = - (qU)total > 0 (q ) < 0 (q ) > 0 Uc Ux with wtotal=(wt)x + (wt)c=0 -(w ) (w ) -(w ) tc tx tx ε c == ε x = so w hat’s the problem ??? (qUc ) (q Uc ) (qUx ) (wtx ) = (q Uc ) ε c (wtx ) = -(q Ux ) ε x q transferred TL → TU with no net work (qLc ) + (q Uc ) + (w tc ) = 0 (qLx ) + (q Ux ) + (w tx ) = 0 violates Clausius statement of second law so w hat’s the solution ??? -(qUx ) εεCx to give -(w)=(w),tx tC , and (q) UC (q) U x (qUC ) εε x C x > c is not a condition consistent with the Second Law ε (q ) (q ) (q ) (q )1 x w h ic h w ill be < 0 , fo r ε > ε Utotal Ux UC UxxC so any Carnot machine, ideal gas or not ε C (q ) (q ) (q ) -(q ) - (w ) + -(q ) + (w ) (q ) Ltotal L x LC U x tx UC tx U total 25 26 any carnot carnot ideal gasTTT U L U so far setup for (HW prob #23) ε efficiency greater than Carnot HW#4 Prob.
Load more

Recommended publications
  • Arxiv:2008.06405V1 [Physics.Ed-Ph] 14 Aug 2020 Fig.1 Shows Four Classical Cycles: (A) Carnot Cycle, (B) Stirling Cycle, (C) Otto Cycle and (D) Diesel Cycle
    Investigating student understanding of heat engine: a case study of Stirling engine Lilin Zhu1 and Gang Xiang1, ∗ 1Department of Physics, Sichuan University, Chengdu 610064, China (Dated: August 17, 2020) We report on the study of student difficulties regarding heat engine in the context of Stirling cycle within upper-division undergraduate thermal physics course. An in-class test about a Stirling engine with a regenerator was taken by three classes, and the students were asked to perform one of the most basic activities—calculate the efficiency of the heat engine. Our data suggest that quite a few students have not developed a robust conceptual understanding of basic engineering knowledge of the heat engine, including the function of the regenerator and the influence of piston movements on the heat and work involved in the engine. Most notably, although the science error ratios of the three classes were similar (∼10%), the engineering error ratios of the three classes were high (above 50%), and the class that was given a simple tutorial of engineering knowledge of heat engine exhibited significantly smaller engineering error ratio by about 20% than the other two classes. In addition, both the written answers and post-test interviews show that most of the students can only associate Carnot’s theorem with Carnot cycle, but not with other reversible cycles working between two heat reservoirs, probably because no enough cycles except Carnot cycle were covered in the traditional Thermodynamics textbook. Our results suggest that both scientific and engineering knowledge are important and should be included in instructional approaches, especially in the Thermodynamics course taught in the countries and regions with a tradition of not paying much attention to experimental education or engineering training.
    [Show full text]
  • The Carnot Cycle, Reversibility and Entropy
    entropy Article The Carnot Cycle, Reversibility and Entropy David Sands Department of Physics and Mathematics, University of Hull, Hull HU6 7RX, UK; [email protected] Abstract: The Carnot cycle and the attendant notions of reversibility and entropy are examined. It is shown how the modern view of these concepts still corresponds to the ideas Clausius laid down in the nineteenth century. As such, they reflect the outmoded idea, current at the time, that heat is motion. It is shown how this view of heat led Clausius to develop the entropy of a body based on the work that could be performed in a reversible process rather than the work that is actually performed in an irreversible process. In consequence, Clausius built into entropy a conflict with energy conservation, which is concerned with actual changes in energy. In this paper, reversibility and irreversibility are investigated by means of a macroscopic formulation of internal mechanisms of damping based on rate equations for the distribution of energy within a gas. It is shown that work processes involving a step change in external pressure, however small, are intrinsically irreversible. However, under idealised conditions of zero damping the gas inside a piston expands and traces out a trajectory through the space of equilibrium states. Therefore, the entropy change due to heat flow from the reservoir matches the entropy change of the equilibrium states. This trajectory can be traced out in reverse as the piston reverses direction, but if the external conditions are adjusted appropriately, the gas can be made to trace out a Carnot cycle in P-V space.
    [Show full text]
  • The Carnot Cycle Ray Fu
    The Carnot Cycle Ray Fu The Carnot Cycle We will investigate some properties of the Carnot cycle and explore the subtleties of Carnot's theorem. 1. Recall that the Carnot cycle consists of the following four reversible steps, in order: (a) isothermal expansion at TH (b) isentropic expansion at Smax (c) isothermal compression at TC (d) isentropic compression at Smin TH and TC represent the temperatures of the hot and cold thermal reservoirs; Smin and Smax represent the minimum and maximum entropy reached by the working fluid in the Carnot cycle. Draw the Carnot cycle on a TS plot and label each step of the cycle, as well as TH , TC , Smin, and Smax. 2. On the same plot, sketch the cycle that results when steps (a) and (c) are respectively replaced with irreversible isothermal expansion and compression, assuming that the resulting cycle operates between the same two entropies Smin and Smax. We will prove geometrically that the Carnot cycle is the most efficient thermodynamic cycle working between the range of temperatures bounded by TH and TC . To this end, consider an arbitrary reversible thermody- namic cycle C with working fluid having maximum and minimum temperatures TH and TC , and maximum and minimum entropies Smax and Smin. It is sufficient to consider reversible cycles, for irreversible cycles must have lower efficiencies by Clausius's inequality. 3. Define two areas A and B on the corresponding TS plot for C. A is the area enclosed by C, whereas B is the area bounded above by the bottom of C, bounded below by the S-axis, and bounded to left and right by the lines S = Smin and S = Smax.
    [Show full text]
  • Thermodynamics Cycle Analysis and Numerical Modeling of Thermoelastic Cooling Systems
    international journal of refrigeration 56 (2015) 65e80 Available online at www.sciencedirect.com ScienceDirect www.iifiir.org journal homepage: www.elsevier.com/locate/ijrefrig Thermodynamics cycle analysis and numerical modeling of thermoelastic cooling systems Suxin Qian, Jiazhen Ling, Yunho Hwang*, Reinhard Radermacher, Ichiro Takeuchi Center for Environmental Energy Engineering, Department of Mechanical Engineering, University of Maryland, 4164 Glenn L. Martin Hall Bldg., College Park, MD 20742, USA article info abstract Article history: To avoid global warming potential gases emission from vapor compression air- Received 3 October 2014 conditioners and water chillers, alternative cooling technologies have recently garnered Received in revised form more and more attentions. Thermoelastic cooling is among one of the alternative candi- 3 March 2015 dates, and have demonstrated promising performance improvement potential on the Accepted 2 April 2015 material level. However, a thermoelastic cooling system integrated with heat transfer fluid Available online 14 April 2015 loops have not been studied yet. This paper intends to bridge such a gap by introducing the single-stage cycle design options at the beginning. An analytical coefficient of performance Keywords: (COP) equation was then derived for one of the options using reverse Brayton cycle design. Shape memory alloy The equation provides physical insights on how the system performance behaves under Elastocaloric different conditions. The performance of the same thermoelastic cooling cycle using NiTi Efficiency alloy was then evaluated based on a dynamic model developed in this study. It was found Nitinol that the system COP was 1.7 for a baseline case considering both driving motor and Solid-state cooling parasitic pump power consumptions, while COP ranged from 5.2 to 7.7 when estimated with future improvements.
    [Show full text]
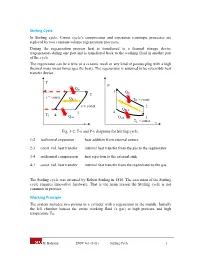
  • Stirling Cycle Working Principle
    Stirling Cycle In Stirling cycle, Carnot cycle’s compression and expansion isentropic processes are replaced by two constant-volume regeneration processes. During the regeneration process heat is transferred to a thermal storage device (regenerator) during one part and is transferred back to the working fluid in another part of the cycle. The regenerator can be a wire or a ceramic mesh or any kind of porous plug with a high thermal mass (mass times specific heat). The regenerator is assumed to be reversible heat transfer device. T P Qin TH 1 1 Q 2 in v = const. Q Reg. TH = const. v = const. 2 QReg. 3 4 TL 4 Qout Qout 3 T = const. s L v Fig. 3-2: T-s and P-v diagrams for Stirling cycle. 1-2 isothermal expansion heat addition from external source 2-3 const. vol. heat transfer internal heat transfer from the gas to the regenerator 3-4 isothermal compression heat rejection to the external sink 4-1 const. vol. heat transfer internal heat transfer from the regenerator to the gas The Stirling cycle was invented by Robert Stirling in 1816. The execution of the Stirling cycle requires innovative hardware. That is the main reason the Stirling cycle is not common in practice. Working Principle The system includes two pistons in a cylinder with a regenerator in the middle. Initially the left chamber houses the entire working fluid (a gas) at high pressure and high temperature TH. M. Bahrami ENSC 461 (S 11) Stirling Cycle 1 TH TL QH State 1 Regenerator Fig 3-3a: 1-2, isothermal heat transfer to the gas at TH from external source.
    [Show full text]
  • Removing the Mystery of Entropy and Thermodynamics – Part IV Harvey S
    Removing the Mystery of Entropy and Thermodynamics – Part IV Harvey S. Leff, Reed College, Portland, ORa,b In Part IV of this five-part series,1–3 reversibility and irreversibility are discussed. The question-answer format of Part I is continued and Key Points 4.1–4.3 are enumerated.. Questions and Answers T < TA. That energy enters through a surface, heats the matter • What is a reversible process? Recall that a near that surface to a temperature greater than T, and subse- reversible process is specified in the Clausius algorithm, quently energy spreads to other parts of the system at lower dS = đQrev /T. To appreciate this subtlety, it is important to un- temperature. The system’s temperature is nonuniform during derstand the significance of reversible processes in thermody- the ensuing energy-spreading process, nonequilibrium ther- namics. Although they are idealized processes that can only be modynamic states are reached, and the process is irreversible. approximated in real life, they are extremely useful. A revers- To approximate reversible heating, say, at constant pres- ible process is typically infinitely slow and sequential, based on sure, one can put a system in contact with many successively a large number of small steps that can be reversed in principle. hotter reservoirs. In Fig. 1 this idea is illustrated using only In the limit of an infinite number of vanishingly small steps, all initial, final, and three intermediate reservoirs, each separated thermodynamic states encountered for all subsystems and sur- by a finite temperature change. Step 1 takes the system from roundings are equilibrium states, and the process is reversible.
    [Show full text]
  • Physics 3700 Carnot Cycle. Heat Engines. Refrigerators. Relevant Sections in Text
    Carnot Cycle. Heat Engines. Refrigerators. Physics 3700 Carnot Cycle. Heat Engines. Refrigerators. Relevant sections in text: x4.1, 4.2 Heat Engines A heat engine is any device which, through a cyclic process, absorbs energy via heat from some external source and converts (some of) this energy to work. Many real world \engines" (e.g., automobile engines, steam engines) can be modeled as heat engines. There are some fundamental thermodynamic features and limitations of heat engines which arise irrespective of the details of how the engines work. Here I will briefly examine some of these since they are useful, instructive, and even interesting. The principal piece of information which thermodynamics gives us about this simple | but rather general | model of an engine is a limitation on the possible efficiency of the engine. The efficiency of a heat engine is defined as the ratio of work performed W to the energy absorbed as heat Qh: W e = : Qh Let me comment on notation and conventions. First of all, note that I use a slightly different symbol for work here. Following standard conventions (including the text's) for discussions of engines (and refrigerators), we deal with the work done by the engine on its environment. So, in the context of heat engines if W > 0 then energy is leaving the thermodynamic system in the form of work. Secondly, the subscript \h" on Qh does not signify \heat", but \hot". The idea here is that in order for energy to flow from the environment into the system the source of that energy must be at a higher temperature than the engine.
    [Show full text]
  • , Equilibrium Composition
    Index absolute activity , 301 benezene, tables and T -$ chart, 158- 9, absolute azeotropy , 379 165 absolute entropy , 411 , 444 , 451 Bernoulli 's equation, 35 absorption refrigeration , 240 - 2 blower, Roots, 214- 16 acentric factor , 468 - 72 boiler , feed-water heating, 273- 8 acid -base equilibrium , 426 - 7 boiling point , see vapour pressure acidity constant , 426 - - , elevation of, 320 activity , 307 Boltzmann's constant, xiii - , absolute , 301 Boltzmann's distribution law, 438, 467 - coefficient , 307 - 18 , 324 , 326 - 8 Boyle's law, see gas, perfect - - , mean 327 , 430 - 1 Boyle temperature, 138 - - , single -ion 326 - 7 Brayton refrigeration cycle, 252- 3 adiabatic compressibility , 151 B -$ chart, 112 - efficiency , 200 , 229 bubble point , 346ft - process , 6 Bunsen coefficient, 323 - - , in a perfect gas, 86 , 193- 4 - reaction , 416 - 20 calorie, thermochemical, 413 adsorption , 331 - 4 calorimetry, 38- 45 advancement , see reaction , extent of carbon dioxide, properties of, 451 affinity , 395 - 6 - - , solid, 246 air , cooling of , 253 Carnot cycle, 56ft, 232ft - , equilibrium composition, 455 - heat engine, 56ft - , liquefaction of , 256 - heat pump, 60- 1 - , separation of , 367 - principle , 62- 5 alcohol , distillation of , 378 - 9 , 386 - refrigerator , 60- 1 allotropy , 343 - 5 cascadeliquefier, 264- 7 alloys , 381 - 2 - refrigeration cycles, 248- 50 Arnagat 's law , 295 - 6, 302 centrifugal compressor, 23, 219, 225- 7 ammonia , heat capacity of , 89- 90, 168 characteristic equations, see fundamental - absorption
    [Show full text]
  • Carnot Cycle
    Summary of heat engines so far - A thermodynamic system in a process Reversible Heat Source connecting state A to state B ∆Q Th RHS T-dynamic - In this process, the system can do work and system emit/absorb heat ∆WRWS - What processes maximize work done by the system? Rev Work Source - We have proven that reversible processes (processes that do not change the total entropy of the system and its environment) maximize Process A →B work done by the system in the process A→B of the system Notes Cyclic Engine -To continuously generate work , a heat engine should go through a Heat source Heat sink cyclic process . ∆Q ∆Q Th h c Tc - Such an engine needs to have a heat source and a heat sink at different temperatures. ∆WRWS Working body - The net result of each cycle is to e. g. rubber band extract heat from the heat source and distribute it between the heat Rev Work Source transferred to the sink and useful work. Notes Carnot cycle As an example, we will consider a particular cycle consisting of two isotherms and two adiabats called the Carnot cycle applied to a rubber band engine. As we will see, Carnot cycle is reversible Here T and S are temperature and entropy of the working body Heat source Heat sink T AB ∆ ∆ T Th Qh Qc Tc h ∆WRWS Working body Tc e. g. rubber band D C Rev Work Source S SA SB Notes 1. Carnot Cycle: Isothermal Contraction (A) (B) T ∆ = 0 h U Th ∆Qsource LB LA Heat source Heat source T h Th T A B Force= Γ Th 2 2 D C cBT (L − L0 ) (L − L0 ) A→B h A B Tc ∆WRWS = ∆Qsource = Th∆S = − S 2 S S L0 L0 A B Notes 2.
    [Show full text]
  • Heat Engines ∆=+E QW Thermo Processes Int • Adiabatic – No Heat Exchanged
    Chapter 19 Heat Engines ∆=+E QW Thermo Processes int • Adiabatic – No heat exchanged – Q = 0 and ∆Eint = W • Isobaric – Constant pressure – W = P (Vf – Vi) and ∆Eint = Q + W • Isochoric – Constant Volume – W = 0 and ∆Eint = Q • Isothermal – Constant temperature V W= nRT ln i ∆Eint = 0 and Q = -W Vf C and C P V Note that for all ideal gases: where R = 8.31 J/mol K is the universal gas constant. Slide 17-80 Heat Engines Refrigerators Important Concepts 2nd Law: Perfect Heat Engine Can NOT exist! No energy is expelled to the cold reservoir It takes in some amount of energy and does an equal amount of work e = 100% It is an impossible engine No Free Lunch! Limit of efficiency is a Carnot Engine Reversible and Irreversible Processes The reversible process is an idealization. All real processes on Earth are irreversible. Example of an approximate reversible process: The gas is compressed isothermally The gas is in contact with an energy reservoir Continually transfer just enough energy to keep the temperature constant The change in entropy is equal to zero for a reversible process and increases for irreversible processes. Section 22.3 The Maximum Efficiency Qc TTcc =andec = 1 − QThh Th Qc Tc Qh Th COPC = = COPH = = W TThc− W TThc− Heat Engines . In a steam turbine of a modern power plant, expanding steam does work by spinning the turbine. The steam is then condensed to liquid water and pumped back to the boiler to start the process again. First heat is transferred to the water in the boiler to create steam, and later heat is transferred out of the water to an external cold reservoir, in the condenser.
    [Show full text]
  • Physics 301 28-Oct-1999 13-1 Superfluid Helium As We Mentioned Last Time, the Transition of 4He at 2.17 K at 1 Atm Is Believed T
    Physics 301 28-Oct-1999 13-1 Superfluid Helium As we mentioned last time, the transition of 4He at 2.17 K at 1 atm is believed to be the condensation of most of the helium atoms into the ground state—a Bose-Einstein condensation. That this does not occur at the calculated temperature of 3.1 K is believed to be due to the fact that there are interactions among helium atoms so that helium cannot really be described as a non-interacting boson gas! Above the transition temperature, helium is refered to as He I and below the transition, it’s called He II. K&K present several reasons why thinking of liquid helium as a non-interacting gas is not totally off the wall. You should read them and also study the phase diagrams for both 4He and 3He (K&K figures 7.14 and 7.15). The fact that something happens at 2.17 K is shown by the heat capacity versus tem- perature curve (figure 7.12 in K&K) which is similar to the heat capacity curve for a phase transition and also not all that different from the curve you’re going to calculate for the Bose-Einstein condensate in the homework problem (despite what the textbook problem actually says about a marked difference in the curves!). In addition to the heat capacity, the mechanical properties of 4He are markedly different below the transition temperature. The liquid helium becomes a superfluid which means it flows without viscosity (that is, friction). The existence of a Bose-Einstein condensate does not necessarily imply the existence of superfluidity.
    [Show full text]
  • Carnot Cycle and Heat Engine Fundamentals and Applications • Michel Feidt Carnot Cycle and Heat Engine Fundamentals and Applications
    Carnot and Cycle Heat Engine Fundamentals and Applications • Michel Feidt Carnot Cycle and Heat Engine Fundamentals and Applications Edited by Michel Feidt Printed Edition of the Special Issue Published in Entropy www.mdpi.com/journal/entropy Carnot Cycle and Heat Engine Fundamentals and Applications Carnot Cycle and Heat Engine Fundamentals and Applications Special Issue Editor Michel Feidt MDPI • Basel • Beijing • Wuhan • Barcelona • Belgrade • Manchester • Tokyo • Cluj • Tianjin Special Issue Editor Michel Feidt Universite´ de Lorraine France Editorial Office MDPI St. Alban-Anlage 66 4052 Basel, Switzerland This is a reprint of articles from the Special Issue published online in the open access journal Entropy (ISSN 1099-4300) (available at: https://www.mdpi.com/journal/entropy/special issues/ carnot cycle). For citation purposes, cite each article independently as indicated on the article page online and as indicated below: LastName, A.A.; LastName, B.B.; LastName, C.C. Article Title. Journal Name Year, Article Number, Page Range. ISBN 978-3-03928-845-8 (Pbk) ISBN 978-3-03928-846-5 (PDF) c 2020 by the authors. Articles in this book are Open Access and distributed under the Creative Commons Attribution (CC BY) license, which allows users to download, copy and build upon published articles, as long as the author and publisher are properly credited, which ensures maximum dissemination and a wider impact of our publications. The book as a whole is distributed by MDPI under the terms and conditions of the Creative Commons license CC BY-NC-ND. Contents About the Special Issue Editor ...................................... vii Michel Feidt Carnot Cycle and Heat Engine: Fundamentals and Applications Reprinted from: Entropy 2020, 22, 348, doi:10.3390/e2203034855 ..................
    [Show full text]