DOCSLIB.ORG

Thermodynamics Cycle Analysis and Numerical Modeling of Thermoelastic Cooling Systems

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Thermodynamics Cycle Analysis and Numerical Modeling of Thermoelastic Cooling Systems international journal of refrigeration 56 (2015) 65e80 Available online at www.sciencedirect.com ScienceDirect www.iifiir.org journal homepage: www.elsevier.com/locate/ijrefrig Thermodynamics cycle analysis and numerical modeling of thermoelastic cooling systems Suxin Qian, Jiazhen Ling, Yunho Hwang*, Reinhard Radermacher, Ichiro Takeuchi Center for Environmental Energy Engineering, Department of Mechanical Engineering, University of Maryland, 4164 Glenn L. Martin Hall Bldg., College Park, MD 20742, USA article info abstract Article history: To avoid global warming potential gases emission from vapor compression air- Received 3 October 2014 conditioners and water chillers, alternative cooling technologies have recently garnered Received in revised form more and more attentions. Thermoelastic cooling is among one of the alternative candi- 3 March 2015 dates, and have demonstrated promising performance improvement potential on the Accepted 2 April 2015 material level. However, a thermoelastic cooling system integrated with heat transfer fluid Available online 14 April 2015 loops have not been studied yet. This paper intends to bridge such a gap by introducing the single-stage cycle design options at the beginning. An analytical coefficient of performance Keywords: (COP) equation was then derived for one of the options using reverse Brayton cycle design. Shape memory alloy The equation provides physical insights on how the system performance behaves under Elastocaloric different conditions. The performance of the same thermoelastic cooling cycle using NiTi Efficiency alloy was then evaluated based on a dynamic model developed in this study. It was found Nitinol that the system COP was 1.7 for a baseline case considering both driving motor and Solid-state cooling parasitic pump power consumptions, while COP ranged from 5.2 to 7.7 when estimated with future improvements. © 2015 Elsevier Ltd and IIR. All rights reserved. Analyse de cycle thermodynamique et modelisation numerique des systemes de refroidissement thermoelastique Mots-cles : Alliage am emoire de forme ; Elastocalorique ; Efficacite ; Nitinol ; Refroidissement al 'etat solide (Sharp et al., 2006), magnetic cooling (Sarlah et al., 2006; Vasile 1. Introduction and Muller, 2006; Zimm et al., 2006; Jacobs et al., 2014), elec- trocaloric cooling (Gu et al., 2013; Jia and Yu, 2012), thermoa- Solid-state cooling technologies have been developed rapidly coustic cooling (Reid et al., 1998; Swift et al., 1999; Yazaki et al., during the past few decades, including thermoelectric cooling 2002), and most recently, thermoelastic cooling (Cui et al., * Corresponding author. Tel.: 1 301 405 5247; fax: 1 301 405 2025. þ þ E-mail address: [email protected] (Y. Hwang). http://dx.doi.org/10.1016/j.ijrefrig.2015.04.001 0140-7007/© 2015 Elsevier Ltd and IIR. All rights reserved. 66 international journal of refrigeration 56 (2015) 65e80 1 Nomenclature u fluid mean velocity [m sÀ ] 1 u* internal energy [J gÀ ] 3 1 Symbols V_ volumetric flow rate [m sÀ ] A material constant related to hysteresis energy W work [J] 1 [J gÀ ] W_ work rate [W] 1 Bi Biot number w specific work [J gÀ ] COP coefficient of performance VCC vapor compression cycle 1 1 2 1 cp specific heat [J gÀ KÀ ] a thermal diffusivity [m sÀ ] D mechanical efficiency loss factor d equivalent thickness [m] e strain ε effectiveness 1 e_ strain change rate [sÀ ] s stress [MPa] F cyclic loss factor g non-dimensional latent heat GWP global warming potential h efficiency 3 g000 generation term in energy equation [W mÀ ] k thermal mass factor 3 HR heat recovery r density [kg mÀ ] HTF heat transfer fluid x martensite phase fraction 1 1 Dh latent heat [J gÀ ] x_ martensite phase fraction change rate [sÀ ] 2 1 h heat transfer coefficient [W mÀ KÀ ] D material constant related to strain [ ] À ID internal diameter [m] Subscripts K material constant related to elasticity [MPa] 1 1 ad adiabatic k thermal conductivity [W mÀ KÀ ] AM austenite to martensite L length [m] cyc cycle m mass [kg] 1 f fluid m_ mass flow rate [kg sÀ ] HT heat transfer OD outside diameter [m] init initial Q heat transferred [J] mat material Q_ capacity [W] 1 mot motor q capacity per unit mass [J gÀ ] MA martensite to austenite RHS right hand side 1 1 rec recovery s specific entropy [J gÀ KÀ ] s solid, solid heat exchanger or bed SMA shape memory alloy sat saturation sec second trsm transmission T temperature [C] loading DT adiabatic temperature span [K] þ ad unloading t time, or duration [s] À t* heat recovery coefficient 2012) (a.k.a. elastocaloric cooling). These solid-state cooling the useful cooling/heating effect is the result of the associated systems offer us alternatives to eliminate the emission of latent heat released during the stress-induced martensitic traditional high global warming potential (GWP) halogenated phase change process, which makes the material transits refrigerants used in the vapor compression cycle (VCC) sys- between the martensite phase and austenite phase. As shown tems. Compared with other alternative cooling methods, in Fig. 1 (a), when the SMA is subjected to an external stress elastocaloric effect has a higher adiabatic temperature span, exceeding the phase change stress ssat, austenite crystal and therefore, it's possible to use a single stage cycle for starts to transform to martensite crystal, and meanwhile re- typical air-conditioning and refrigeration applications. A more leases the latent heat to raise SMA's temperature at the same sophisticated ranking of solid-state materials also indicates time. The cooling effect takes place when the external system that thermoelastic cooling materials are better than materials stress is less than the ssat. As the stress decreases below the used for magnetic cooling (Qian et al., 2015) in terms of the threshold, the material transits back to the “parent” state, the material level performance. Therefore, from thermodynamics austenite state, and absorbs ambient heat. The SMA was perspective, thermoelastic cooling can be easily applied to famous for its unique mechanical property that it “re- cooling systems as compared to its competitive technologies. members” an original “trained” shape, and can return to this Thermoelastic cooling technology uses shape memory pre-deformed shape upon heating above a transitional tem- alloy (SMA), which is a group of metal alloys with significant perature. NiTi alloy and copper based alloys are most widely elastocaloric effect. They can be used for power cycle, or used as engineering functional materials for a variety of ap- applied reversely for thermoelastic cooling/heat pump cycles. plications, including automotive, aerospace, mini actuators In a power cycle, the driving potential is the temperature and sensors, biomedical, and orthopedic surgery (Jani et al., difference. While in a heat pump cycle, the applied stress in- 2014). As the market of SMA grows, the cost of SMA reduces duces the cooling and heating. In a cooling/heat pump cycle, and it is now possible to use them for power generation and international journal of refrigeration 56 (2015) 65e80 67 Fig. 1 e Illustration of martensitic phase change processes. cooling/heat pump systems. Significant theoretical in- models and finite element or finite volume methods have vestigations for SMA heat engines have been carried out (Tong been carried out in the past decade. and Wayman, 1974; Ahler, 1975; Wayman and Tong, 1975; There are two concerns for the current literature of SMA Delaey and Lepeleire, 1976; Cunningham and Ashbee, 1977; heat engines. First, most of the simple equilibrium analysis and Ziolkowski, 1993), and a few prototypes were built (Sato the sophisticated dynamic model used the homogeneity et al., 2008; Kanada, 2008; Kaneko and Enomoto, 2009; assumption, which is in fact quite common in continuum Wakjira, 2001; Schiller, 2002) and simulated (Gil and Planell, mechanics and thermodynamics. However, applying such 1999; Liu, 2004; Zhu et al., 2001a, 2001b) in the past few de- simplification to complicated shape memory alloy phase cades. Existing SMA heat engines were either wire based change could deviate from reality to a significant amount under wheels (Sato et al., 2008; Kanada, 2008; Kaneko and Enomoto, some circumstances (Furst et al., 2012). To avoid complexity in 2009; Wakjira, 2001), or spring-based on twin crank design calculation of the work needed to drive the cooling/heat pump (Schiller, 2002). A common design of SMA heat engine's heat cycle, experimental data were used to fit in a simple one- source is a hot water bath, with an air cooled heat sink, dimensional constitutive model, in order to evaluate the therefore no complicated fluid lines are necessary. The simple loading/unloading energy related to the coefficient of perfor- design reduced the structural complexity, but left no room for mance (COP) for this study. Such a decoupling of stressestrain applying heat regeneration between the cold SMA wire going relation from temperature allows for better understanding of into the hot water bath, and hot SMA wire leaving hot water the system level performance, rather than focusing on all the bath, as indicated by Fig. 2. Besides heat transfer, the work details of the material level performance. This practice will not production is another essential part when it comes to evaluate lose much accuracy on the material level as long as real the power generation efficiency. Early works on deriving the experimental loading/unloading data are applied. analytical efficiency relies on simple equilibrium stresse- Second, for simplicity consideration, neither the previous strain model (Tong and Wayman, 1974; Ahler, 1975; Wayman analytical approach nor the simulation in the literature and Tong, 1975; Delaey and Lepeleire, 1976; Cunningham and considered heat recovery/regeneration process to improve the Ashbee, 1977), where only a single stress-saturation temper- efficiency. Besides, the control volume of the system they ature is needed and the computation of work is simple. Recent considered is only the SMA itself, excluding any heat transfer computation using analytical approach (Ziolkowski, 1993) fluid loops and associated losses.
Load more

Recommended publications
  • Arxiv:2008.06405V1 [Physics.Ed-Ph] 14 Aug 2020 Fig.1 Shows Four Classical Cycles: (A) Carnot Cycle, (B) Stirling Cycle, (C) Otto Cycle and (D) Diesel Cycle
    Investigating student understanding of heat engine: a case study of Stirling engine Lilin Zhu1 and Gang Xiang1, ∗ 1Department of Physics, Sichuan University, Chengdu 610064, China (Dated: August 17, 2020) We report on the study of student difficulties regarding heat engine in the context of Stirling cycle within upper-division undergraduate thermal physics course. An in-class test about a Stirling engine with a regenerator was taken by three classes, and the students were asked to perform one of the most basic activities—calculate the efficiency of the heat engine. Our data suggest that quite a few students have not developed a robust conceptual understanding of basic engineering knowledge of the heat engine, including the function of the regenerator and the influence of piston movements on the heat and work involved in the engine. Most notably, although the science error ratios of the three classes were similar (∼10%), the engineering error ratios of the three classes were high (above 50%), and the class that was given a simple tutorial of engineering knowledge of heat engine exhibited significantly smaller engineering error ratio by about 20% than the other two classes. In addition, both the written answers and post-test interviews show that most of the students can only associate Carnot’s theorem with Carnot cycle, but not with other reversible cycles working between two heat reservoirs, probably because no enough cycles except Carnot cycle were covered in the traditional Thermodynamics textbook. Our results suggest that both scientific and engineering knowledge are important and should be included in instructional approaches, especially in the Thermodynamics course taught in the countries and regions with a tradition of not paying much attention to experimental education or engineering training.
    [Show full text]
  • Equilibrium Thermodynamics
    Equilibrium Thermodynamics Instructor: - Clare Yu (e-mail [email protected], phone: 824-6216) - office hours: Wed from 2:30 pm to 3:30 pm in Rowland Hall 210E Textbooks: - primary: Herbert Callen “Thermodynamics and an Introduction to Thermostatistics” - secondary: Frederick Reif “Statistical and Thermal Physics” - secondary: Kittel and Kroemer “Thermal Physics” - secondary: Enrico Fermi “Thermodynamics” Grading: - weekly homework: 25% - discussion problems: 10% - midterm exam: 30% - final exam: 35% Equilibrium Thermodynamics Material Covered: Equilibrium thermodynamics, phase transitions, critical phenomena (~ 10 first chapters of Callen’s textbook) Homework: - Homework assignments posted on course website Exams: - One midterm, 80 minutes, Tuesday, May 8 - Final, 2 hours, Tuesday, June 12, 10:30 am - 12:20 pm - All exams are in this room 210M RH Course website is at http://eiffel.ps.uci.edu/cyu/p115B/class.html The Subject of Thermodynamics Thermodynamics describes average properties of macroscopic matter in equilibrium. - Macroscopic matter: large objects that consist of many atoms and molecules. - Average properties: properties (such as volume, pressure, temperature etc) that do not depend on the detailed positions and velocities of atoms and molecules of macroscopic matter. Such quantities are called thermodynamic coordinates, variables or parameters. - Equilibrium: state of a macroscopic system in which all average properties do not change with time. (System is not driven by external driving force.) Why Study Thermodynamics ? - Thermodynamics predicts that the average macroscopic properties of a system in equilibrium are not independent from each other. Therefore, if we measure a subset of these properties, we can calculate the rest of them using thermodynamic relations. - Thermodynamics not only gives the exact description of the state of equilibrium but also provides an approximate description (to a very high degree of precision!) of relatively slow processes.
    [Show full text]
  • Statistical Thermodynamics - Fall 2009
    1 Statistical Thermodynamics - Fall 2009 Professor Dmitry Garanin Thermodynamics September 9, 2012 I. PREFACE The course of Statistical Thermodynamics consist of two parts: Thermodynamics and Statistical Physics. These both branches of physics deal with systems of a large number of particles (atoms, molecules, etc.) at equilibrium. 3 19 One cm of an ideal gas under normal conditions contains NL =2.69 10 atoms, the so-called Loschmidt number. Although one may describe the motion of the atoms with the help of× Newton’s equations, direct solution of such a large number of differential equations is impossible. On the other hand, one does not need the too detailed information about the motion of the individual particles, the microscopic behavior of the system. One is rather interested in the macroscopic quantities, such as the pressure P . Pressure in gases is due to the bombardment of the walls of the container by the flying atoms of the contained gas. It does not exist if there are only a few gas molecules. Macroscopic quantities such as pressure arise only in systems of a large number of particles. Both thermodynamics and statistical physics study macroscopic quantities and relations between them. Some macroscopics quantities, such as temperature and entropy, are non-mechanical. Equilibruim, or thermodynamic equilibrium, is the state of the system that is achieved after some time after time-dependent forces acting on the system have been switched off. One can say that the system approaches the equilibrium, if undisturbed. Again, thermodynamic equilibrium arises solely in macroscopic systems. There is no thermodynamic equilibrium in a system of a few particles that are moving according to the Newton’s law.
    [Show full text]
  • Szilard-1929.Pdf
    In memory of Leo Szilard, who passed away on May 30,1964, we present an English translation of his classical paper ober die Enfropieuerminderung in einem thermodynamischen System bei Eingrifen intelligenter Wesen, which appeared in the Zeitschrift fur Physik, 1929,53,840-856. The publica- tion in this journal of this translation was approved by Dr. Szilard before he died, but he never saw the copy. At Mrs. Szilard’s request, Dr. Carl Eckart revised the translation. This is one of the earliest, if not the earliest paper, in which the relations of physical entropy to information (in the sense of modem mathematical theory of communication) were rigorously demonstrated and in which Max- well’s famous demon was successfully exorcised: a milestone in the integra- tion of physical and cognitive concepts. ON THE DECREASE OF ENTROPY IN A THERMODYNAMIC SYSTEM BY THE INTERVENTION OF INTELLIGENT BEINGS by Leo Szilard Translated by Anatol Rapoport and Mechthilde Knoller from the original article “Uber die Entropiever- minderung in einem thermodynamischen System bei Eingriffen intelligenter Wesen.” Zeitschrift fur Physik, 1929, 65, 840-866. 0*3 resulting quantity of entropy. We find that The objective of the investigation is to it is exactly as great as is necessary for full find the conditions which apparently allow compensation. The actual production of the construction of a perpetual-motion ma- entropy in connection with the measure- chine of the second kind, if one permits an ment, therefore, need not be greater than intelligent being to intervene in a thermo- Equation (1) requires. dynamic system. When such beings make F(J measurements, they make the system behave in a manner distinctly different from the way HERE is an objection, already historical, a mechanical system behaves when left to Tagainst the universal validity of the itself.
    [Show full text]
  • Thermodynamic Processes: the Limits of Possible
    Thermodynamic Processes: The Limits of Possible Thermodynamics put severe restrictions on what processes involving a change of the thermodynamic state of a system (U,V,N,…) are possible. In a quasi-static process system moves from one equilibrium state to another via a series of other equilibrium states . All quasi-static processes fall into two main classes: reversible and irreversible processes . Processes with decreasing total entropy of a thermodynamic system and its environment are prohibited by Postulate II Notes Graphic representation of a single thermodynamic system Phase space of extensive coordinates The fundamental relation S(1) =S(U (1) , X (1) ) of a thermodynamic system defines a hypersurface in the coordinate space S(1) S(1) U(1) U(1) X(1) X(1) S(1) – entropy of system 1 (1) (1) (1) (1) (1) U – energy of system 1 X = V , N 1 , …N m – coordinates of system 1 Notes Graphic representation of a composite thermodynamic system Phase space of extensive coordinates The fundamental relation of a composite thermodynamic system S = S (1) (U (1 ), X (1) ) + S (2) (U-U(1) ,X (2) ) (system 1 and system 2). defines a hyper-surface in the coordinate space of the composite system S(1+2) S(1+2) U (1,2) X = V, N 1, …N m – coordinates U of subsystems (1 and 2) X(1,2) (1,2) S – entropy of a composite system X U – energy of a composite system Notes Irreversible and reversible processes If we change constraints on some of the composite system coordinates, (e.g.
    [Show full text]
  • The Carnot Cycle, Reversibility and Entropy
    entropy Article The Carnot Cycle, Reversibility and Entropy David Sands Department of Physics and Mathematics, University of Hull, Hull HU6 7RX, UK; [email protected] Abstract: The Carnot cycle and the attendant notions of reversibility and entropy are examined. It is shown how the modern view of these concepts still corresponds to the ideas Clausius laid down in the nineteenth century. As such, they reflect the outmoded idea, current at the time, that heat is motion. It is shown how this view of heat led Clausius to develop the entropy of a body based on the work that could be performed in a reversible process rather than the work that is actually performed in an irreversible process. In consequence, Clausius built into entropy a conflict with energy conservation, which is concerned with actual changes in energy. In this paper, reversibility and irreversibility are investigated by means of a macroscopic formulation of internal mechanisms of damping based on rate equations for the distribution of energy within a gas. It is shown that work processes involving a step change in external pressure, however small, are intrinsically irreversible. However, under idealised conditions of zero damping the gas inside a piston expands and traces out a trajectory through the space of equilibrium states. Therefore, the entropy change due to heat flow from the reservoir matches the entropy change of the equilibrium states. This trajectory can be traced out in reverse as the piston reverses direction, but if the external conditions are adjusted appropriately, the gas can be made to trace out a Carnot cycle in P-V space.
    [Show full text]
  • INTRODUCTION to Thermodynamic Properties Introduction to Thermodynamic Properties
    INTRODUCTION TO Thermodynamic Properties Introduction to Thermodynamic Properties © 1998–2018 COMSOL Protected by patents listed on www.comsol.com/patents, and U.S. Patents 7,519,518; 7,596,474; 7,623,991; 8,219,373; 8,457,932; 8,954,302; 9,098,106; 9,146,652; 9,323,503; 9,372,673; and 9,454,625. Patents pending. This Documentation and the Programs described herein are furnished under the COMSOL Software License Agreement (www.comsol.com/comsol-license-agreement) and may be used or copied only under the terms of the license agreement. COMSOL, the COMSOL logo, COMSOL Multiphysics, COMSOL Desktop, COMSOL Server, and LiveLink are either registered trademarks or trademarks of COMSOL AB. All other trademarks are the property of their respective owners, and COMSOL AB and its subsidiaries and products are not affiliated with, endorsed by, sponsored by, or supported by those trademark owners. For a list of such trademark owners, see www.comsol.com/trademarks. Version: COMSOL 5.4 Contact Information Visit the Contact COMSOL page at www.comsol.com/contact to submit general inquiries, contact Technical Support, or search for an address and phone number. You can also visit the Worldwide Sales Offices page at www.comsol.com/contact/offices for address and contact information. If you need to contact Support, an online request form is located at the COMSOL Access page at www.comsol.com/support/case. Other useful links include: • Support Center: www.comsol.com/support • Product Download: www.comsol.com/product-download • Product Updates: www.comsol.com/support/updates •COMSOL Blog: www.comsol.com/blogs • Discussion Forum: www.comsol.com/community •Events: www.comsol.com/events • COMSOL Video Gallery: www.comsol.com/video • Support Knowledge Base: www.comsol.com/support/knowledgebase Part number: CM021603 Contents The Thermodynamic Properties Data Base .
    [Show full text]
  • The Carnot Cycle Ray Fu
    The Carnot Cycle Ray Fu The Carnot Cycle We will investigate some properties of the Carnot cycle and explore the subtleties of Carnot's theorem. 1. Recall that the Carnot cycle consists of the following four reversible steps, in order: (a) isothermal expansion at TH (b) isentropic expansion at Smax (c) isothermal compression at TC (d) isentropic compression at Smin TH and TC represent the temperatures of the hot and cold thermal reservoirs; Smin and Smax represent the minimum and maximum entropy reached by the working fluid in the Carnot cycle. Draw the Carnot cycle on a TS plot and label each step of the cycle, as well as TH , TC , Smin, and Smax. 2. On the same plot, sketch the cycle that results when steps (a) and (c) are respectively replaced with irreversible isothermal expansion and compression, assuming that the resulting cycle operates between the same two entropies Smin and Smax. We will prove geometrically that the Carnot cycle is the most efficient thermodynamic cycle working between the range of temperatures bounded by TH and TC . To this end, consider an arbitrary reversible thermody- namic cycle C with working fluid having maximum and minimum temperatures TH and TC , and maximum and minimum entropies Smax and Smin. It is sufficient to consider reversible cycles, for irreversible cycles must have lower efficiencies by Clausius's inequality. 3. Define two areas A and B on the corresponding TS plot for C. A is the area enclosed by C, whereas B is the area bounded above by the bottom of C, bounded below by the S-axis, and bounded to left and right by the lines S = Smin and S = Smax.
    [Show full text]
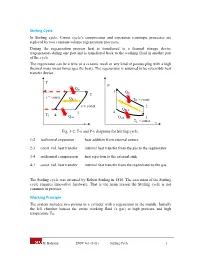
  • Stirling Cycle Working Principle
    Stirling Cycle In Stirling cycle, Carnot cycle’s compression and expansion isentropic processes are replaced by two constant-volume regeneration processes. During the regeneration process heat is transferred to a thermal storage device (regenerator) during one part and is transferred back to the working fluid in another part of the cycle. The regenerator can be a wire or a ceramic mesh or any kind of porous plug with a high thermal mass (mass times specific heat). The regenerator is assumed to be reversible heat transfer device. T P Qin TH 1 1 Q 2 in v = const. Q Reg. TH = const. v = const. 2 QReg. 3 4 TL 4 Qout Qout 3 T = const. s L v Fig. 3-2: T-s and P-v diagrams for Stirling cycle. 1-2 isothermal expansion heat addition from external source 2-3 const. vol. heat transfer internal heat transfer from the gas to the regenerator 3-4 isothermal compression heat rejection to the external sink 4-1 const. vol. heat transfer internal heat transfer from the regenerator to the gas The Stirling cycle was invented by Robert Stirling in 1816. The execution of the Stirling cycle requires innovative hardware. That is the main reason the Stirling cycle is not common in practice. Working Principle The system includes two pistons in a cylinder with a regenerator in the middle. Initially the left chamber houses the entire working fluid (a gas) at high pressure and high temperature TH. M. Bahrami ENSC 461 (S 11) Stirling Cycle 1 TH TL QH State 1 Regenerator Fig 3-3a: 1-2, isothermal heat transfer to the gas at TH from external source.
    [Show full text]
  • 12/8 and 12/10/2010
    PY105 C1 1. Help for Final exam has been posted on WebAssign. 2. The Final exam will be on Wednesday December 15th from 6-8 pm. First Law of Thermodynamics 3. You will take the exam in multiple rooms, divided as follows: SCI 107: Abbasi to Fasullo, as well as Khajah PHO 203: Flynn to Okuda, except for Khajah SCI B58: Ordonez to Zhang 1 2 Heat and Work done by a Gas Thermodynamics Initial: Consider a cylinder of ideal Thermodynamics is the study of systems involving gas at room temperature. Suppose the piston on top of energy in the form of heat and work. the cylinder is free to move vertically without friction. When the cylinder is placed in a container of hot water, heat Equilibrium: is transferred into the cylinder. Where does the heat energy go? Why does the volume increase? 3 4 The First Law of Thermodynamics The First Law of Thermodynamics The First Law is often written as: Some of the heat energy goes into raising the temperature of the gas (which is equivalent to raising the internal energy of the gas). The rest of it does work by raising the piston. ΔEQWint =− Conservation of energy leads to: QEW=Δ + int (the first law of thermodynamics) This form of the First Law says that the change in internal energy of a system is Q is the heat added to a system (or removed if it is negative) equal to the heat supplied to the system Eint is the internal energy of the system (the energy minus the work done by the system (usually associated with the motion of the atoms and/or molecules).
    [Show full text]
  • Removing the Mystery of Entropy and Thermodynamics – Part IV Harvey S
    Removing the Mystery of Entropy and Thermodynamics – Part IV Harvey S. Leff, Reed College, Portland, ORa,b In Part IV of this five-part series,1–3 reversibility and irreversibility are discussed. The question-answer format of Part I is continued and Key Points 4.1–4.3 are enumerated.. Questions and Answers T < TA. That energy enters through a surface, heats the matter • What is a reversible process? Recall that a near that surface to a temperature greater than T, and subse- reversible process is specified in the Clausius algorithm, quently energy spreads to other parts of the system at lower dS = đQrev /T. To appreciate this subtlety, it is important to un- temperature. The system’s temperature is nonuniform during derstand the significance of reversible processes in thermody- the ensuing energy-spreading process, nonequilibrium ther- namics. Although they are idealized processes that can only be modynamic states are reached, and the process is irreversible. approximated in real life, they are extremely useful. A revers- To approximate reversible heating, say, at constant pres- ible process is typically infinitely slow and sequential, based on sure, one can put a system in contact with many successively a large number of small steps that can be reversed in principle. hotter reservoirs. In Fig. 1 this idea is illustrated using only In the limit of an infinite number of vanishingly small steps, all initial, final, and three intermediate reservoirs, each separated thermodynamic states encountered for all subsystems and sur- by a finite temperature change. Step 1 takes the system from roundings are equilibrium states, and the process is reversible.
    [Show full text]
  • 16. the First Law of Thermodynamics
    16. The First Law of Thermodynamics Introduction and Summary The First Law of Thermodynamics is basically a statement of Conservation of Energy. The total energy of a thermodynamic system is called the Internal Energy U. A system can have its Internal Energy changed (DU) in two major ways: (1) Heat Q can flow into the system from the surroundings and (2) the system can do work W on the surroundings. The concept of Heat Energy Q has been discussed previously in connection with Specific Heat c and the Latent Heats of fusion and vaporization at phase transitions. Here, we will focus on the Heat Q absorbed or given off by an ideal gas. Also, the Work W done by an ideal gas will be calculated. Both heat and work are energy, and it is important to understand the difference between the heat Q and the work W. Thermodynamic Work W Previously, we understood the concept of Mechanical Work in connection with Newton's Laws of Motion. There the focus was work done ON THE SYSTEM. For example, the work done on a mass M in raising it up a height h against gravity is W=Mgh. Thermodynamic Work is similar to Mechanical Work BUT in Thermodynamic Work the focus is on the work done BY THE SYSTEM. Historically, Thermodynamics was developed in order to understand the work done BY heat engines like the steam engine. So when a system (like a heat engine) does work ON its surroundings, then the Thermodynamic Work is POSITIVE. (This is the opposite for Mechanical Work.) If work is done on the heat engine, the Thermodynamic Work is NEGATIVE.
    [Show full text]