Choice of Optimal Shift Parameter for the Intruder State Removal Techniques in Multireference Perturbation Theory Shu-Wei Chang and Henryk A
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Supporting Information
Electronic Supplementary Material (ESI) for RSC Advances. This journal is © The Royal Society of Chemistry 2020 Supporting Information How to Select Ionic Liquids as Extracting Agent Systematically? Special Case Study for Extractive Denitrification Process Shurong Gaoa,b,c,*, Jiaxin Jina,b, Masroor Abroc, Ruozhen Songc, Miao Hed, Xiaochun Chenc,* a State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Beijing, 102206, China b Research Center of Engineering Thermophysics, North China Electric Power University, Beijing, 102206, China c Beijing Key Laboratory of Membrane Science and Technology & College of Chemical Engineering, Beijing University of Chemical Technology, Beijing 100029, PR China d Office of Laboratory Safety Administration, Beijing University of Technology, Beijing 100124, China * Corresponding author, Tel./Fax: +86-10-6443-3570, E-mail: [email protected], [email protected] 1 COSMO-RS Computation COSMOtherm allows for simple and efficient processing of large numbers of compounds, i.e., a database of molecular COSMO files; e.g. the COSMObase database. COSMObase is a database of molecular COSMO files available from COSMOlogic GmbH & Co KG. Currently COSMObase consists of over 2000 compounds including a large number of industrial solvents plus a wide variety of common organic compounds. All compounds in COSMObase are indexed by their Chemical Abstracts / Registry Number (CAS/RN), by a trivial name and additionally by their sum formula and molecular weight, allowing a simple identification of the compounds. We obtained the anions and cations of different ILs and the molecular structure of typical N-compounds directly from the COSMObase database in this manuscript. -

GROMACS: Fast, Flexible, and Free
GROMACS: Fast, Flexible, and Free DAVID VAN DER SPOEL,1 ERIK LINDAHL,2 BERK HESS,3 GERRIT GROENHOF,4 ALAN E. MARK,4 HERMAN J. C. BERENDSEN4 1Department of Cell and Molecular Biology, Uppsala University, Husargatan 3, Box 596, S-75124 Uppsala, Sweden 2Stockholm Bioinformatics Center, SCFAB, Stockholm University, SE-10691 Stockholm, Sweden 3Max-Planck Institut fu¨r Polymerforschung, Ackermannweg 10, D-55128 Mainz, Germany 4Groningen Biomolecular Sciences and Biotechnology Institute, University of Groningen, Nijenborgh 4, NL-9747 AG Groningen, The Netherlands Received 12 February 2005; Accepted 18 March 2005 DOI 10.1002/jcc.20291 Published online in Wiley InterScience (www.interscience.wiley.com). Abstract: This article describes the software suite GROMACS (Groningen MAchine for Chemical Simulation) that was developed at the University of Groningen, The Netherlands, in the early 1990s. The software, written in ANSI C, originates from a parallel hardware project, and is well suited for parallelization on processor clusters. By careful optimization of neighbor searching and of inner loop performance, GROMACS is a very fast program for molecular dynamics simulation. It does not have a force field of its own, but is compatible with GROMOS, OPLS, AMBER, and ENCAD force fields. In addition, it can handle polarizable shell models and flexible constraints. The program is versatile, as force routines can be added by the user, tabulated functions can be specified, and analyses can be easily customized. Nonequilibrium dynamics and free energy determinations are incorporated. Interfaces with popular quantum-chemical packages (MOPAC, GAMES-UK, GAUSSIAN) are provided to perform mixed MM/QM simula- tions. The package includes about 100 utility and analysis programs. -

Chem Compute Quickstart
Chem Compute Quickstart Chem Compute is maintained by Mark Perri at Sonoma State University and hosted on Jetstream at Indiana University. The Chem Compute URL is https://chemcompute.org/. We will use Chem Compute as the frontend for running electronic structure calculations with The General Atomic and Molecular Electronic Structure System, GAMESS (http://www.msg.ameslab.gov/gamess/). Chem Compute also provides access to other computational chemistry resources including PSI4 and the molecular dynamics packages TINKER and NAMD, though we will not be using those resource at this time. Follow this link, https://chemcompute.org/gamess/submit, to directly access the Chem Compute GAMESS guided submission interface. If you are a returning Chem Computer user, please log in now. If your University is part of the InCommon Federation you can log in without registering by clicking Login then "Log In with Google or your University" – select your University from the dropdown list. Otherwise if this is your first time working with Chem Compute, please register as a Chem Compute user by clicking the “Register” link in the top-right corner of the page. This gives you access to all of the computational resources available at ChemCompute.org and will allow you to maintain copies of your calculations in your user “Dashboard” that you can refer to later. Registering also helps track usage and obtain the resources needed to continue providing its service. When logged in with the GAMESS-Submit tabs selected, an instruction section appears on the left side of the page with instructions for several different kinds of calculations. -

Popular GPU-Accelerated Applications
LIFE & MATERIALS SCIENCES GPU-ACCELERATED APPLICATIONS | CATALOG | AUG 12 LIFE & MATERIALS SCIENCES APPLICATIONS CATALOG Application Description Supported Features Expected Multi-GPU Release Status Speed Up* Support Bioinformatics BarraCUDA Sequence mapping software Alignment of short sequencing 6-10x Yes Available now reads Version 0.6.2 CUDASW++ Open source software for Smith-Waterman Parallel search of Smith- 10-50x Yes Available now protein database searches on GPUs Waterman database Version 2.0.8 CUSHAW Parallelized short read aligner Parallel, accurate long read 10x Yes Available now aligner - gapped alignments to Version 1.0.40 large genomes CATALOG GPU-BLAST Local search with fast k-tuple heuristic Protein alignment according to 3-4x Single Only Available now blastp, multi cpu threads Version 2.2.26 GPU-HMMER Parallelized local and global search with Parallel local and global search 60-100x Yes Available now profile Hidden Markov models of Hidden Markov Models Version 2.3.2 mCUDA-MEME Ultrafast scalable motif discovery algorithm Scalable motif discovery 4-10x Yes Available now based on MEME algorithm based on MEME Version 3.0.12 MUMmerGPU A high-throughput DNA sequence alignment Aligns multiple query sequences 3-10x Yes Available now LIFE & MATERIALS& LIFE SCIENCES APPLICATIONS program against reference sequence in Version 2 parallel SeqNFind A GPU Accelerated Sequence Analysis Toolset HW & SW for reference 400x Yes Available now assembly, blast, SW, HMM, de novo assembly UGENE Opensource Smith-Waterman for SSE/CUDA, Fast short -

Starting SCF Calculations by Superposition of Atomic Densities
Starting SCF Calculations by Superposition of Atomic Densities J. H. VAN LENTHE,1 R. ZWAANS,1 H. J. J. VAN DAM,2 M. F. GUEST2 1Theoretical Chemistry Group (Associated with the Department of Organic Chemistry and Catalysis), Debye Institute, Utrecht University, Padualaan 8, 3584 CH Utrecht, The Netherlands 2CCLRC Daresbury Laboratory, Daresbury WA4 4AD, United Kingdom Received 5 July 2005; Accepted 20 December 2005 DOI 10.1002/jcc.20393 Published online in Wiley InterScience (www.interscience.wiley.com). Abstract: We describe the procedure to start an SCF calculation of the general type from a sum of atomic electron densities, as implemented in GAMESS-UK. Although the procedure is well known for closed-shell calculations and was already suggested when the Direct SCF procedure was proposed, the general procedure is less obvious. For instance, there is no need to converge the corresponding closed-shell Hartree–Fock calculation when dealing with an open-shell species. We describe the various choices and illustrate them with test calculations, showing that the procedure is easier, and on average better, than starting from a converged minimal basis calculation and much better than using a bare nucleus Hamiltonian. © 2006 Wiley Periodicals, Inc. J Comput Chem 27: 926–932, 2006 Key words: SCF calculations; atomic densities Introduction hrstuhl fur Theoretische Chemie, University of Kahrlsruhe, Tur- bomole; http://www.chem-bio.uni-karlsruhe.de/TheoChem/turbo- Any quantum chemical calculation requires properly defined one- mole/),12 GAMESS(US) (Gordon Research Group, GAMESS, electron orbitals. These orbitals are in general determined through http://www.msg.ameslab.gov/GAMESS/GAMESS.html, 2005),13 an iterative Hartree–Fock (HF) or Density Functional (DFT) pro- Spartan (Wavefunction Inc., SPARTAN: http://www.wavefun. -

Parameterizing a Novel Residue
University of Illinois at Urbana-Champaign Luthey-Schulten Group, Department of Chemistry Theoretical and Computational Biophysics Group Computational Biophysics Workshop Parameterizing a Novel Residue Rommie Amaro Brijeet Dhaliwal Zaida Luthey-Schulten Current Editors: Christopher Mayne Po-Chao Wen February 2012 CONTENTS 2 Contents 1 Biological Background and Chemical Mechanism 4 2 HisH System Setup 7 3 Testing out your new residue 9 4 The CHARMM Force Field 12 5 Developing Topology and Parameter Files 13 5.1 An Introduction to a CHARMM Topology File . 13 5.2 An Introduction to a CHARMM Parameter File . 16 5.3 Assigning Initial Values for Unknown Parameters . 18 5.4 A Closer Look at Dihedral Parameters . 18 6 Parameter generation using SPARTAN (Optional) 20 7 Minimization with new parameters 32 CONTENTS 3 Introduction Molecular dynamics (MD) simulations are a powerful scientific tool used to study a wide variety of systems in atomic detail. From a standard protein simulation, to the use of steered molecular dynamics (SMD), to modelling DNA-protein interactions, there are many useful applications. With the advent of massively parallel simulation programs such as NAMD2, the limits of computational anal- ysis are being pushed even further. Inevitably there comes a time in any molecular modelling scientist’s career when the need to simulate an entirely new molecule or ligand arises. The tech- nique of determining new force field parameters to describe these novel system components therefore becomes an invaluable skill. Determining the correct sys- tem parameters to use in conjunction with the chosen force field is only one important aspect of the process. -
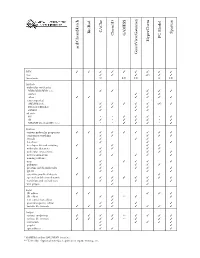
D:\Doc\Workshops\2005 Molecular Modeling\Notebook Pages\Software Comparison\Summary.Wpd
CAChe BioRad Spartan GAMESS Chem3D PC Model HyperChem acd/ChemSketch GaussView/Gaussian WIN TTTT T T T T T mac T T T (T) T T linux/unix U LU LU L LU Methods molecular mechanics MM2/MM3/MM+/etc. T T T T T Amber T T T other TT T T T T semi-empirical AM1/PM3/etc. T T T T T (T) T Extended Hückel T T T T ZINDO T T T ab initio HF * * T T T * T dft T * T T T * T MP2/MP4/G1/G2/CBS-?/etc. * * T T T * T Features various molecular properties T T T T T T T T T conformer searching T T T T T crystals T T T data base T T T developer kit and scripting T T T T molecular dynamics T T T T molecular interactions T T T T movies/animations T T T T T naming software T nmr T T T T T polymers T T T T proteins and biomolecules T T T T T QSAR T T T T scientific graphical objects T T spectral and thermodynamic T T T T T T T T transition and excited state T T T T T web plugin T T Input 2D editor T T T T T 3D editor T T ** T T text conversion editor T protein/sequence editor T T T T various file formats T T T T T T T T Output various renderings T T T T ** T T T T various file formats T T T T ** T T T animation T T T T T graphs T T spreadsheet T T T * GAMESS and/or GAUSSIAN interface ** Text only. -

Kepler Gpus and NVIDIA's Life and Material Science
LIFE AND MATERIAL SCIENCES Mark Berger; [email protected] Founded 1993 Invented GPU 1999 – Computer Graphics Visual Computing, Supercomputing, Cloud & Mobile Computing NVIDIA - Core Technologies and Brands GPU Mobile Cloud ® ® GeForce Tegra GRID Quadro® , Tesla® Accelerated Computing Multi-core plus Many-cores GPU Accelerator CPU Optimized for Many Optimized for Parallel Tasks Serial Tasks 3-10X+ Comp Thruput 7X Memory Bandwidth 5x Energy Efficiency How GPU Acceleration Works Application Code Compute-Intensive Functions Rest of Sequential 5% of Code CPU Code GPU CPU + GPUs : Two Year Heart Beat 32 Volta Stacked DRAM 16 Maxwell Unified Virtual Memory 8 Kepler Dynamic Parallelism 4 Fermi 2 FP64 DP GFLOPS GFLOPS per DP Watt 1 Tesla 0.5 CUDA 2008 2010 2012 2014 Kepler Features Make GPU Coding Easier Hyper-Q Dynamic Parallelism Speedup Legacy MPI Apps Less Back-Forth, Simpler Code FERMI 1 Work Queue CPU Fermi GPU CPU Kepler GPU KEPLER 32 Concurrent Work Queues Developer Momentum Continues to Grow 100M 430M CUDA –Capable GPUs CUDA-Capable GPUs 150K 1.6M CUDA Downloads CUDA Downloads 1 50 Supercomputer Supercomputers 60 640 University Courses University Courses 4,000 37,000 Academic Papers Academic Papers 2008 2013 Explosive Growth of GPU Accelerated Apps # of Apps Top Scientific Apps 200 61% Increase Molecular AMBER LAMMPS CHARMM NAMD Dynamics GROMACS DL_POLY 150 Quantum QMCPACK Gaussian 40% Increase Quantum Espresso NWChem Chemistry GAMESS-US VASP CAM-SE 100 Climate & COSMO NIM GEOS-5 Weather WRF Chroma GTS 50 Physics Denovo ENZO GTC MILC ANSYS Mechanical ANSYS Fluent 0 CAE MSC Nastran OpenFOAM 2010 2011 2012 SIMULIA Abaqus LS-DYNA Accelerated, In Development NVIDIA GPU Life Science Focus Molecular Dynamics: All codes are available AMBER, CHARMM, DESMOND, DL_POLY, GROMACS, LAMMPS, NAMD Great multi-GPU performance GPU codes: ACEMD, HOOMD-Blue Focus: scaling to large numbers of GPUs Quantum Chemistry: key codes ported or optimizing Active GPU acceleration projects: VASP, NWChem, Gaussian, GAMESS, ABINIT, Quantum Espresso, BigDFT, CP2K, GPAW, etc. -
![Modern Quantum Chemistry with [Open]Molcas](https://docslib.b-cdn.net/cover/4742/modern-quantum-chemistry-with-open-molcas-744742.webp)
Modern Quantum Chemistry with [Open]Molcas
Modern quantum chemistry with [Open]Molcas Cite as: J. Chem. Phys. 152, 214117 (2020); https://doi.org/10.1063/5.0004835 Submitted: 17 February 2020 . Accepted: 11 May 2020 . Published Online: 05 June 2020 Francesco Aquilante , Jochen Autschbach , Alberto Baiardi , Stefano Battaglia , Veniamin A. Borin , Liviu F. Chibotaru , Irene Conti , Luca De Vico , Mickaël Delcey , Ignacio Fdez. Galván , Nicolas Ferré , Leon Freitag , Marco Garavelli , Xuejun Gong , Stefan Knecht , Ernst D. Larsson , Roland Lindh , Marcus Lundberg , Per Åke Malmqvist , Artur Nenov , Jesper Norell , Michael Odelius , Massimo Olivucci , Thomas B. Pedersen , Laura Pedraza-González , Quan M. Phung , Kristine Pierloot , Markus Reiher , Igor Schapiro , Javier Segarra-Martí , Francesco Segatta , Luis Seijo , Saumik Sen , Dumitru-Claudiu Sergentu , Christopher J. Stein , Liviu Ungur , Morgane Vacher , Alessio Valentini , and Valera Veryazov J. Chem. Phys. 152, 214117 (2020); https://doi.org/10.1063/5.0004835 152, 214117 © 2020 Author(s). The Journal ARTICLE of Chemical Physics scitation.org/journal/jcp Modern quantum chemistry with [Open]Molcas Cite as: J. Chem. Phys. 152, 214117 (2020); doi: 10.1063/5.0004835 Submitted: 17 February 2020 • Accepted: 11 May 2020 • Published Online: 5 June 2020 Francesco Aquilante,1,a) Jochen Autschbach,2,b) Alberto Baiardi,3,c) Stefano Battaglia,4,d) Veniamin A. Borin,5,e) Liviu F. Chibotaru,6,f) Irene Conti,7,g) Luca De Vico,8,h) Mickaël Delcey,9,i) Ignacio Fdez. Galván,4,j) Nicolas Ferré,10,k) Leon Freitag,3,l) Marco Garavelli,7,m) Xuejun Gong,11,n) Stefan Knecht,3,o) Ernst D. Larsson,12,p) Roland Lindh,4,q) Marcus Lundberg,9,r) Per Åke Malmqvist,12,s) Artur Nenov,7,t) Jesper Norell,13,u) Michael Odelius,13,v) Massimo Olivucci,8,14,w) Thomas B. -

Benchmarking and Application of Density Functional Methods In
BENCHMARKING AND APPLICATION OF DENSITY FUNCTIONAL METHODS IN COMPUTATIONAL CHEMISTRY by BRIAN N. PAPAS (Under Direction the of Henry F. Schaefer III) ABSTRACT Density Functional methods were applied to systems of chemical interest. First, the effects of integration grid quadrature choice upon energy precision were documented. This was done through application of DFT theory as implemented in five standard computational chemistry programs to a subset of the G2/97 test set of molecules. Subsequently, the neutral hydrogen-loss radicals of naphthalene, anthracene, tetracene, and pentacene and their anions where characterized using five standard DFT treatments. The global and local electron affinities were computed for the twelve radicals. The results for the 1- naphthalenyl and 2-naphthalenyl radicals were compared to experiment, and it was found that B3LYP appears to be the most reliable functional for this type of system. For the larger systems the predicted site specific adiabatic electron affinities of the radicals are 1.51 eV (1-anthracenyl), 1.46 eV (2-anthracenyl), 1.68 eV (9-anthracenyl); 1.61 eV (1-tetracenyl), 1.56 eV (2-tetracenyl), 1.82 eV (12-tetracenyl); 1.93 eV (14-pentacenyl), 2.01 eV (13-pentacenyl), 1.68 eV (1-pentacenyl), and 1.63 eV (2-pentacenyl). The global minimum for each radical does not have the same hydrogen removed as the global minimum for the analogous anion. With this in mind, the global (or most preferred site) adiabatic electron affinities are 1.37 eV (naphthalenyl), 1.64 eV (anthracenyl), 1.81 eV (tetracenyl), and 1.97 eV (pentacenyl). In later work, ten (scandium through zinc) homonuclear transition metal trimers were studied using one DFT 2 functional. -
![Arxiv:1911.06836V1 [Physics.Chem-Ph] 8 Aug 2019 A](https://docslib.b-cdn.net/cover/0105/arxiv-1911-06836v1-physics-chem-ph-8-aug-2019-a-950105.webp)
Arxiv:1911.06836V1 [Physics.Chem-Ph] 8 Aug 2019 A
Multireference electron correlation methods: Journeys along potential energy surfaces Jae Woo Park,1, ∗ Rachael Al-Saadon,2 Matthew K. MacLeod,3 Toru Shiozaki,2, 4 and Bess Vlaisavljevich5, y 1Department of Chemistry, Chungbuk National University, Chungdae-ro 1, Cheongju 28644, Korea. 2Department of Chemistry, Northwestern University, 2145 Sheridan Rd., Evanston, IL 60208, USA. 3Workday, 4900 Pearl Circle East, Suite 100, Boulder, CO 80301, USA. 4Quantum Simulation Technologies, Inc., 625 Massachusetts Ave., Cambridge, MA 02139, USA. 5Department of Chemistry, University of South Dakota, 414 E. Clark Street, Vermillion, SD 57069, USA. (Dated: November 19, 2019) Multireference electron correlation methods describe static and dynamical electron correlation in a balanced way, and therefore, can yield accurate and predictive results even when single-reference methods or multicon- figurational self-consistent field (MCSCF) theory fails. One of their most prominent applications in quantum chemistry is the exploration of potential energy surfaces (PES). This includes the optimization of molecular ge- ometries, such as equilibrium geometries and conical intersections, and on-the-fly photodynamics simulations; both depend heavily on the ability of the method to properly explore the PES. Since such applications require the nuclear gradients and derivative couplings, the availability of analytical nuclear gradients greatly improves the utility of quantum chemical methods. This review focuses on the developments and advances made in the past two decades. To motivate the readers, we first summarize the notable applications of multireference elec- tron correlation methods to mainstream chemistry, including geometry optimizations and on-the-fly dynamics. Subsequently, we review the analytical nuclear gradient and derivative coupling theories for these methods, and the software infrastructure that allows one to make use of these quantities in applications. -

Jaguar 5.5 User Manual Copyright © 2003 Schrödinger, L.L.C
Jaguar 5.5 User Manual Copyright © 2003 Schrödinger, L.L.C. All rights reserved. Schrödinger, FirstDiscovery, Glide, Impact, Jaguar, Liaison, LigPrep, Maestro, Prime, QSite, and QikProp are trademarks of Schrödinger, L.L.C. MacroModel is a registered trademark of Schrödinger, L.L.C. To the maximum extent permitted by applicable law, this publication is provided “as is” without warranty of any kind. This publication may contain trademarks of other companies. October 2003 Contents Chapter 1: Introduction.......................................................................................1 1.1 Conventions Used in This Manual.......................................................................2 1.2 Citing Jaguar in Publications ...............................................................................3 Chapter 2: The Maestro Graphical User Interface...........................................5 2.1 Starting Maestro...................................................................................................5 2.2 The Maestro Main Window .................................................................................7 2.3 Maestro Projects ..................................................................................................7 2.4 Building a Structure.............................................................................................9 2.5 Atom Selection ..................................................................................................10 2.6 Toolbar Controls ................................................................................................11