COMBINATIONAL CIRCUITS I (Adders, Decoders, Multiplexers)
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Comparison of Parallel and Pipelined CORDIC Algorithm Using RCA and CSA
Comparison of Parallel and Pipelined CORDIC algorithm using RCA and CSA Diego Barragan´ Guerrero Lu´ıs Geraldo P. Meloni FEEC - UNICAMP FEEC - UNICAMP Campinas, Sao˜ Paulo, Brazil, 13083-852 Campinas, Sao˜ Paulo, Brazil, 13083-852 +5519 9308-9952 +5519 9778-1523 [email protected] [email protected] Abstract— This paper presents an implementation of the algorithm has two modes of operation: the rotational mode CORDIC algorithm in digital hardware using two types of (RM) where the vector (xi; yi) is rotated by an angle θ to algebraic adders: Ripple-Carry Adder (RCA) and Carry-Select obtain a new vector (x ; y ), and the vectoring mode (VM) Adder (CSA), both in parallel and pipelined architectures. Anal- N N ysis of time performance and resources utilization was carried in which the algorithm computes the modulus R and phase α out by changing the algorithm number of iterations. These results from the x-axis of the vector (x0; y0). The basic principle of demonstrate the efficiency in operating frequency of the pipelined the algorithm is shown in Figure 1. architecture with respect to the parallel architecture. Also it is shown that the use of CSA reduce the timing processing without significantly increasing the slice use. The code was synthesized us- ing FPGA development tools for the Xilinx Spartan-3E xc3s500e ' ' E N y family. N E N Index Terms— CORDIC, pipelined, parallel, RCA, CSA, y N trigonometrics functions. Rotação Pseudo-rotação R N I. INTRODUCTION E i In Digital Signal Processing with FPGA, trigonometric y i R i functions are used in many signal algorithms, for instance N synchronization and equalization [12]. -

Basics of Logic Design Arithmetic Logic Unit (ALU) Today's Lecture
Basics of Logic Design Arithmetic Logic Unit (ALU) CPS 104 Lecture 9 Today’s Lecture • Homework #3 Assigned Due March 3 • Project Groups assigned & posted to blackboard. • Project Specification is on Web Due April 19 • Building the building blocks… Outline • Review • Digital building blocks • An Arithmetic Logic Unit (ALU) Reading Appendix B, Chapter 3 © Alvin R. Lebeck CPS 104 2 Review: Digital Design • Logic Design, Switching Circuits, Digital Logic Recall: Everything is built from transistors • A transistor is a switch • It is either on or off • On or off can represent True or False Given a bunch of bits (0 or 1)… • Is this instruction a lw or a beq? • What register do I read? • How do I add two numbers? • Need a method to reason about complex expressions © Alvin R. Lebeck CPS 104 3 Review: Boolean Functions • Boolean functions have arguments that take two values ({T,F} or {0,1}) and they return a single or a set of ({T,F} or {0,1}) value(s). • Boolean functions can always be represented by a table called a “Truth Table” • Example: F: {0,1}3 -> {0,1}2 a b c f1f2 0 0 0 0 1 0 0 1 1 1 0 1 0 1 0 0 1 1 0 0 1 0 0 1 0 1 1 0 0 1 1 1 1 1 1 © Alvin R. Lebeck CPS 104 4 Review: Boolean Functions and Expressions F(A, B, C) = (A * B) + (~A * C) ABCF 0000 0011 0100 0111 1000 1010 1101 1111 © Alvin R. Lebeck CPS 104 5 Review: Boolean Gates • Gates are electronics devices that implement simple Boolean functions Examples a a AND(a,b) OR(a,b) a NOT(a) b b a XOR(a,b) a NAND(a,b) b b a NOR(a,b) a XNOR(a,b) b b © Alvin R. -

Implementation of Carry Tree Adders and Compare with RCA and CSLA
International Journal of Emerging Engineering Research and Technology Volume 4, Issue 1, January 2016, PP 1-11 ISSN 2349-4395 (Print) & ISSN 2349-4409 (Online) Implementation of Carry Tree Adders and Compare with RCA and CSLA 1 2 G. Venkatanaga Kumar , C.H Pushpalatha Department of ECE, GONNA INSTITUTE OF TECHNOLOGY, Vishakhapatnam, India (PG Scholar) Department of ECE, GONNA INSTITUTE OF TECHNOLOGY, Vishakhapatnam, India (Associate Professor) ABSTRACT The binary adder is the critical element in most digital circuit designs including digital signal processors (DSP) and microprocessor data path units. As such, extensive research continues to be focused on improving the power delay performance of the adder. In VLSI implementations, parallel-prefix adders are known to have the best performance. Binary adders are one of the most essential logic elements within a digital system. In addition, binary adders are also helpful in units other than Arithmetic Logic Units (ALU), such as multipliers, dividers and memory addressing. Therefore, binary addition is essential that any improvement in binary addition can result in a performance boost for any computing system and, hence, help improve the performance of the entire system. Parallel-prefix adders (also known as carry-tree adders) are known to have the best performance in VLSI designs. This paper investigates three types of carry-tree adders (the Kogge- Stone, sparse Kogge-Stone, Ladner-Fischer and spanning tree adder) and compares them to the simple Ripple Carry Adder (RCA) and Carry Skip Adder (CSA). In this project Xilinx-ISE tool is used for simulation, logical verification, and further synthesizing. This algorithm is implemented in Xilinx 13.2 version and verified using Spartan 3e kit. -
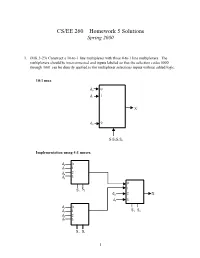
CS/EE 260 – Homework 5 Solutions Spring 2000
CS/EE 260 – Homework 5 Solutions Spring 2000 1. (MK 3-23) Construct a 10-to-1 line multiplexer with three 4-to-1 line multiplexers. The multiplexers should be interconnected and inputs labeled so that the selection codes 0000 through 1001 can be directly applied to the multiplexer selections inputs without added logic. 10:1 mux d0 0 1 d1 1 X d9 9 S3S2S1S0 Implementation using 4:1 muxes. d0 0 d2 1 d4 2 d6 3 0 S 1 S2 1 d8 2 X d9 3 d 0 1 S S d3 1 3 0 d5 2 d7 3 S2 S1 1 2. (MK 3-27) Implement a binary full adder with a dual 4-to-1 line multiplexer and a single inverter. AB Ci S Co 00 0 0 0 C 0 00 1 1 i 0 01 0 1 0 C ´ C 01 1 0 i 1 i 10 0 1 0 10 1 0Ci´ 1 Ci 11 0 0 1 C 1 11 1 1 i 1 0 C 1 i 4:1 2 S 3 mux S1 S0 A B 0 0 1 4:1 Co 2 mux 1 3 S1S0 2 3. (MK 3-34) Design a combinational circuit that forms the 2-bit binary sum S1S0 of two 2-bit numbers A1A0 and B1B0 and has both input C0 and a carry output C2. Do not use half adders or full adders, but instead use a two-level circuit plus inverters for the input variables, as needed. Design the circuit by starting with the following equations for each of the two bits of the adder. -

UNIT 8B a Full Adder
UNIT 8B Computer Organization: Levels of Abstraction 15110 Principles of Computing, 1 Carnegie Mellon University - CORTINA A Full Adder C ABCin Cout S in 0 0 0 A 0 0 1 0 1 0 B 0 1 1 1 0 0 1 0 1 C S out 1 1 0 1 1 1 15110 Principles of Computing, 2 Carnegie Mellon University - CORTINA 1 A Full Adder C ABCin Cout S in 0 0 0 0 0 A 0 0 1 0 1 0 1 0 0 1 B 0 1 1 1 0 1 0 0 0 1 1 0 1 1 0 C S out 1 1 0 1 0 1 1 1 1 1 ⊕ ⊕ S = A B Cin ⊕ ∧ ∨ ∧ Cout = ((A B) C) (A B) 15110 Principles of Computing, 3 Carnegie Mellon University - CORTINA Full Adder (FA) AB 1-bit Cout Full Cin Adder S 15110 Principles of Computing, 4 Carnegie Mellon University - CORTINA 2 Another Full Adder (FA) http://students.cs.tamu.edu/wanglei/csce350/handout/lab6.html AB 1-bit Cout Full Cin Adder S 15110 Principles of Computing, 5 Carnegie Mellon University - CORTINA 8-bit Full Adder A7 B7 A2 B2 A1 B1 A0 B0 1-bit 1-bit 1-bit 1-bit ... Cout Full Full Full Full Cin Adder Adder Adder Adder S7 S2 S1 S0 AB 8 ⁄ ⁄ 8 C 8-bit C out FA in ⁄ 8 S 15110 Principles of Computing, 6 Carnegie Mellon University - CORTINA 3 Multiplexer (MUX) • A multiplexer chooses between a set of inputs. D1 D 2 MUX F D3 D ABF 4 0 0 D1 AB 0 1 D2 1 0 D3 1 1 D4 http://www.cise.ufl.edu/~mssz/CompOrg/CDAintro.html 15110 Principles of Computing, 7 Carnegie Mellon University - CORTINA Arithmetic Logic Unit (ALU) OP 1OP 0 Carry In & OP OP 0 OP 1 F 0 0 A ∧ B 0 1 A ∨ B 1 0 A 1 1 A + B http://cs-alb-pc3.massey.ac.nz/notes/59304/l4.html 15110 Principles of Computing, 8 Carnegie Mellon University - CORTINA 4 Flip Flop • A flip flop is a sequential circuit that is able to maintain (save) a state. -

Design of High Speed and Low Power Six Transistor Full Adder Using Two Transistor Xor Gate
International Journal of Electronics, Communication & Instrumentation Engineering Research and Development (IJECIERD) ISSN 2249-684X Vol. 3, Issue 1, Mar 2013, 87-96 © TJPRC Pvt. Ltd. DESIGN OF HIGH SPEED AND LOW POWER SIX TRANSISTOR FULL ADDER USING TWO TRANSISTOR XOR GATE B. DILLI KUMAR, K. CHARAN KUMAR & T. NAVEEN KUMAR M. Tech (VLSI), Department of ECE, Sree Vidyanikethan Engineering College (Autonomous), Tirupati, India ABSTRACT Full adder is one of the major components in the design of many sophisticated hardware circuits. In this paper the full adder has been designed by using a new efficient design with less number of transistors. A 2 transistor XOR gate has been proposed with the help of two PMOS (Positive Metal Oxide Semiconductor) transistors. By using this 2T XOR gate the size of the full adder has been decreased to a large extent which can be implemented with only 6 transistors. The proposed full adder has a significant improvement in silicon area and power delay product when compared to the previous 8T full adder circuits. Further the proposed adder requires less area to perform a required logic function. Further, the proposed full adder has less power dissipation which makes it suitable for many of the low power applications and because of less area requirement the proposed design can be used in many of the portable applications also . KEYWORDS: Full Adder, XOR, Less Area, Speed, Low Power, Delay, Less Transistor Count, Low Power VLSI INTRODUCTION Full adder is one of the basic building blocks of many of the digital VLSI circuits. Several refinements has been made regarding its structure since its invention. -

Half Adder, Which Finds the Sum of Two Bits
CMSC 313 COMPUTER ORGANIZATION & ASSEMBLY LANGUAGE PROGRAMMING LECTURE 21, SPRING 2013 TOPICS TODAY • Circuits for Addition • Standard Logic Components • Logisim Demo CIRCUITS FOR ADDITION 3.5 Combinational Circuits • Combinational logic circuits give us many useful devices. • One of the simplest is the half adder, which finds the sum of two bits. • We can gain some insight as to the construction of a half adder by looking at its truth table, shown at the right. 30 Half Adder • Inputs: A and B • Outputs: S = lower bit of A + B, cout = carry bit A B S cout 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 • Using Sum-of-Products: S = AB + AB, cout = AB. • Alternatively, we could use XOR: S = A ⊕ B. ! ! ! ! 1 3.5 Combinational Circuits • As we see, the sum can be found using the XOR operation and the carry using the AND operation. 31 3.5 Combinational Circuits • We can change our half adder into to a full adder by including gates for processing the carry bit. • The truth table for a full adder is shown at the right. 32 Full Adder • Inputs: A, B and cin • Outputs: S = lower bit of A + B, cout = carry bit A B cin S cout 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 1 1 0 1 1 0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 1 1 1 1 • S = A BC + ABC + AB C + ABC = A ⊕ B ⊕ C. -

Lecture 4 Adders
Lecture 4 Adders Computer Systems Laboratory Stanford University [email protected] Copyright © 2006 Mark Horowitz Some figures from High-Performance Microprocessor Design © IEEE M Horowitz EE 371 Lecture 4 1 Overview • Readings • Today’s topics – Fast adders generally use a tree structure for parallelism – We will cover basic tree terminology and structures – Look at a few example adder architectures – Examples will spill into next lecture as well M Horowitz EE 371 Lecture 4 2 Adders • Task of an adder is conceptually simple – Sum[n:0]=A[n:0]+B[n:0]+C0 – Subtractors also very simple: -B = ~B+1, so invert B and set C0=1 • Per bit formulas –Sumi = Ai XOR Bi XOR Ci – Couti = Ci+1 = majority(Ai,Bi,Ci) • Fundamental problem is calculating the carry to the nth bit – All carry terms are dependent on all previous terms – So LSB input has a fanout of n • And an absolute minimum of log4n FO4 delays without any logic M Horowitz EE 371 Lecture 4 3 Single-Bit Adders • Adders are chock-full of XORs, which make them interesting – One of the few circuits where pass-gate logic is attractive – A complicated differential passgate logic (DPL) block from the text Lousy way to draw a pair of inverters M Horowitz EE 371 Lecture 4 4 G and P and K, Oh My! • Most fast adders “G”enerate, “P”ropagate, or “K”ill the carry – Usually only G and P are used; K only appears in some carry chains • When does a bit Generate a carry out? –Gi = Ai AND Bi – If Gi is true, then Couti = Ci+1 is forced to be true • When does a bit Propagate a carry in to the carry out? –Pi -

On the Design and Analysis of Quaternary Serial and Parallel Adders
On the Design and Analysis of Quaternary Serial and Parallel Adders Anindya Das1, Ifat Jahangir2 Masud Hasan Department of Electrical and Electronic Engineering Department of Computer Science and Engineering Bangladesh University of Engineering and Technology Bangladesh University of Engineering and Technology Dhaka, Bangladesh Dhaka, Bangladesh [email protected], [email protected] [email protected] Abstract— Optimization techniques for decreasing the time and the operators and the associated algebra to design different area of adder circuits have been extensively studied for years kinds of adders. We have presented the expressions for half mostly in binary logic system. In this paper, we provide the adder and full adder in quaternary logic system in section IV. necessary equations required to design a full adder in quaternary The expressions for propagate and generate values of each logic system. We develop the equations for single-stage parallel qudit are also presented and a complete design of single-stage adder which works as a carry look-ahead adder. We also provide carry look-ahead adder in quaternary logic is demonstrated. the design of a logarithmic stage parallel adder which can Then we have proposed a design of logarithmic stage carry- compute the carries within log2(n) time delay for n qudits. At last, tree adder which has time delay of log2(n) due to its tree we compare the designs and finally propose a hybrid adder which structure and optimal fan-in. In section V we have discussed combines the advantages of serial and parallel adder. the comparative performance of our proposed adders Keywords- Quaternary fast adder, Logarithmic time adder, thoroughly with respect to different significant criteria at the Sparse adder, Hybrid adder. -

Computer Arithmetic
Computer Arithmetic MIPS Integer Representation Logical, Integer Addition & Subtraction 32-bit signed integers, e.g., for numeric operations Chapter 3.1-3.3 • 2’s complement: one representationrepresentation for zero, balanced, allows add/subtract to be treated uniformly EEC170 FQ 2005 32-bit unsigned integers, e.g., for address operations • Address considered 32-bit unsigned integer Provides distinct instructions for signed/unsigned: • ADD, ADDI: add signed register, add signed immediate à causes exception on overflow • ADDU, ADDIU: add unsigned register, add unsigned immediate à no exception on overflow OP Rs Rt Rd 0 ADD/U ADDI/U Rs Rt immediate data Layout of a full adder cell 1 2 Comparison Sign Extension Distinct instructions for comparison of Sign of immediate data extended to form 32-bit signed/unsigned integers representation: • Which is larger: 1111...1111 or 0000...0000 ? Depends of type, signed or unsigned 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 0 1 0 1 0 1 0 1 0 1 0 0 Two versions of slt for signed/unsigned: • slt, sltu: set less than signed, unsigned 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 0 OP Rs Rt Rd 0 SLT/U Thus, ALU always uses 32-bit operands Two versions of immediate comparison also provided: • slti, sltiu: set less than immediate signed, unsigned Extension occurs for signed and unsigned arithmetic SLTI/U Rs Rt immediate data 3 4 Overflow Computer System, Top Level View MIPS has no flag (status) register • complicates pipeline (see Chapter 6) Compiler Overflow (underflow): • Occurs if operands are same sign, result is different sign. -

Adders: Efficient Multiple Input
EFFICIENT MULTI-INPUT ADDITION (CARRY-SAVE) Building Efficient Multiple-input Adders 1. Figure out: algorithm, format conversion if needed, word alignment, sign extension, rounding, etc. 2. Draw “dot diagram” of inputs (one dot per bit) 3. Cover with carry-save adder blocks as appropriate 4. Repeat step #3 until there are two output terms 5. Calculate final result with CPA (carry-propagate adder) 6. Things to check (as a reminder) – Output width sufficient – Inputs sign extended if necessary – Only calculate necessary output bits © B. Baas 88 3:2 Adder Row • Compresses 3 words (4-bit a, b, c in this example) to two words a b c c s © B. Baas 89 3:2 Adder Row • No “sideways” carry signals to a neighboring 3:2 adder even though it would be correct logically (it would cause a slow ripple) • Having said that, it is ok if limited to a small number of ripples in special cases x c s © B. Baas 90 4:2 Adder Row • Compresses 4 words (4-bit a, b, c, d in this example) to two words a b co c d © B. Baas 91 4:2 Adder Row • Remember ci and co signals on the ends of the row of 4:2 adders co ci © B. Baas 92 Carry-save Adder Building Blocks • Notice that to eliminate or “compress” one dot requires approximately 1 “Full adder of hardware” – A 4:2 adder can be made with two full adders 4:2 (really 5:3) 3:2 or Full adder • 4 dots 2 dots • 3 dots 2 dots (actually 5 dots 3 dots) • Compresses 1 dot • Compresses 2 dots • “1 FA” hardware © B. -

Comparative Study on Transistor Based Full Adder Designs
Available online at www.worldscientificnews.com WSN 53(3) (2016) 404-416 EISSN 2392-2192 Comparative study on transistor based full adder designs R. Anitha School of Electronics Engineering, VIT University, Vellore, Tamil Nadu, India E-mail address: [email protected] ABSTRACT Recently in the generic systems the load on the processor is much heavy. The ability and the challenging process have ended with larger core operations are in the core processor. This paper is basically given special importance on different methodologies having been proposed for Adder, which is the basic operation of the Arithmetic unit. The wide research on the digital adders has been covered so many applications like designs of ALU, RISC, CISC processors, DSP used for data path arithmetic, low power CMOS, optical computing, Nanotechnology and so on. This paper gives greater knowledge and understanding about the various techniques that have amply used of Adder from the earlier years. In this paper we analyzed the implementation of different types of full Adders implemented using CMOS logic (Static CMOS and Dynamic CMOS), CMOS Transmission Gates, Pass Transistor Gates (CPL and DPL). Keywords: Full Adder; CPL; DPL; CMOS; Transmission gates; Arithmetic Unit 1. INTRODUCTION In the ALU, the most important arithmetic is the Full Adder block. Full adder is the basic unit in almost all computational circuits. Low power techniques applied on Full Adder block can reduce the computational power consumption. Several full adder circuits have been proposed targeting on design accents such as power, delay, speed and area [1]. World Scientific News 53(3) (2016) 404-416 Digital Logic Circuit implementation can be done by using so many various designs Techniques.