DOCSLIB.ORG

Multi‐Bit Adder/Subtractor with Overflow

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Multi‐Bit Adder/Subtractor with Overflow L07: Circuit Building Blocks I CSE369, Winter 2017 Intro to Digital Design Circuit Building Blocks I Instructor: Justin Hsia L07: Circuit Building Blocks I CSE369, Winter 2017 Practice: String Recognizer FSM Recognize the string 101 with the following behavior . Input: 1 0 0 1 0 1 0 1 1 0 0 1 0 . Output: 0 0 0 0 0 1 0 1 0 0 0 0 0 State diagram to implementation: 2 L07: Circuit Building Blocks I CSE369, Winter 2017 Administrivia Lab 7 – Useful Components . Modifying Lab 6 game to implement common circuit elements • Counter, Shift Registers covered later in lecture . Build a tunable computer opponent . Bonus points for smaller resource usage Quiz 2 is next week in lecture . First 25 minutes, worth 11% of your course grade . On Lectures 4‐6: Sequential Logic, Timing, FSMs, and Verilog . Au16 Quiz 2 (+ solutions) on website: Files Quizzes 3 L07: Circuit Building Blocks I CSE369, Winter 2017 Motivating Example Problem: Implement a simple pocket calculator Need: . Display: Seven segment displays . Inputs: Switches . Math: Arithmetic & Logic Unit (ALU) 4 L07: Circuit Building Blocks I CSE369, Winter 2017 Data Multiplexor Multiplexor (“MUX”) is a selector . Direct one of many ( = s) ‐bit wide inputs onto output . Called a ‐bit, ‐to‐1 MUX Example: ‐bit 2‐to‐1 MUX . Input S ( bits wide) selects between two inputs of bits each This input is passed to output if selector bits inputs match shown value 5 L07: Circuit Building Blocks I CSE369, Winter 2017 Review: Implementing a 1‐bit 2‐to‐1 MUX Schematic: Boolean Algebra: sabc Truth Table: 0 0 00 0 0 10 Circuit Diagram: 0 1 01 0 1 11 100 0 101 1 110 0 111 1 6 L07: Circuit Building Blocks I CSE369, Winter 2017 1‐bit 4‐to‐1 MUX Schematic: Truth Table: How many rows? 26 Boolean Expression: e = s1’s0’a + s1’s0b + s1s0’c + s1s0d 7 L07: Circuit Building Blocks I CSE369, Winter 2017 1‐bit 4‐to‐1 MUX Can we leverage what we’ve previously built? . Alternative hierarchical approach: 8 L07: Circuit Building Blocks I CSE369, Winter 2017 Multiplexers in General Logic Implement with a 8:1 MUX 0 1 2 3 4 8:1 5 MUX 6 7 S0 S1 S2 9 L07: Circuit Building Blocks I CSE369, Winter 2017 Review: Unsigned Integers Unsigned values follow the standard base 2 system . In bits, represent integers to Add and subtract using the normal “carry” and “borrow” rules, just in binary 63 00111111 64 01000000 +8 +00001000 -8 -00001000 71 01000111 56 00111000 10 L07: Circuit Building Blocks I CSE369, Winter 2017 Review: Two’s Complement (Signed) b has weight 2 , other bits have usual weights 2 bw‐1 bw‐2 . b0 Properties: . In bits, represent integers to . Positive number encodings match –1 + 0 unsigned numbers –2 1111 0000 + 1 –3 1110 0001 + 2 . Single zero (encoding = all zeros) 1101 0010 –4 + 3 1100 0011 Negation procedure: Two’s Complement . Take the bitwise complement –5 1011 0100 + 4 and then add one 1010 0101 –6 + 5 ( ~x + 1 == -x ) 1001 0110 –7 1000 0111 + 6 –8 + 7 11 L07: Circuit Building Blocks I CSE369, Winter 2017 Addition and Subtraction in Hardware The same bit manipulations work for both unsigned and two’s complement numbers! . Perform subtraction via adding the negated 2nd operand: 4‐bit examples: Two’s Un Two’s Un 0010 +2 2 1000 -8 8 +1100 -412 +0100 +4 4 0110 +6 6 1111 -115 -0010 +2 2 -1110 -214 12 L07: Circuit Building Blocks I CSE369, Winter 2017 Half Adder (1 bit) Carry Sum Carry‐out bit a0 b0 c1 s0 0000 0101 1001 1110 13 L07: Circuit Building Blocks I CSE369, Winter 2017 Full Adder (1 bit) Possible carry‐in c1 Carry‐in Carry‐out ci ai bi ci+1 si 00000 00101 01001 01110 10001 10110 11010 11111 14 L07: Circuit Building Blocks I CSE369, Winter 2017 Multi‐Bit Adder ( bits) Chain 1‐bit adders by connecting CarryOuti to CarryIni1: b0 + + + 15 L07: Circuit Building Blocks I CSE369, Winter 2017 Subtraction? Can we use our multi‐bit adder to do subtraction? . Flip the bits and add 1? • X⊕1X • CarryIn0 (using full adder in all positions) b0 + + + 16 L07: Circuit Building Blocks I CSE369, Winter 2017 Multi‐bit Adder/Subtractor ⊕1̅ Add 1 (flips the bits) +++ This signal is only high when you perform subtraction 17 L07: Circuit Building Blocks I CSE369, Winter 2017 Detecting Arithmetic Overflow Overflow: When a calculation produces a result that can’t be represented in the current encoding scheme . Integer range limited by fixed width . Can occur in both the positive and negative directions Signed Overflow . Result of add/sub is > TMax or < TMin . ( ) + ( ) = ( ) or ( ) + ( ) = ( ) 18 L07: Circuit Building Blocks I CSE369, Winter 2017 Signed Overflow Examples Two’s Two’s 0101 +5 1001 -7 +0011 +3 +1110 -2 Two’s Two’s 0101 +5 1101 -3 +0010 +2 +1011 -5 19 L07: Circuit Building Blocks I CSE369, Winter 2017 Multi‐bit Adder/Subtractor with Overflow +++ 20 L07: Circuit Building Blocks I CSE369, Winter 2017 Arithmetic and Logic Unit (ALU) Most processors contain a special logic block called the “Arithmetic and Logic Unit” (ALU) . Here’s an easy one that does ADD, SUB, bitwise AND, and bitwise OR (for 32‐bit numbers) Schematic: when S=00, R = A+B when S=01, R = A–B when S=10, R = A&B when S=11, R = A|B L07: Circuit Building Blocks I CSE369, Winter 2017 Simple ALU Schematic Notice that 3 values are ALWAYS calculated in parallel, but only 1 makes it to the Result L07: Circuit Building Blocks I CSE369, Winter 2017 1‐bit Adders in Verilog What’s wrong with this? module halfadd1 (s, a, b); output reg s; . Truncation! input a, b; always @(*) begin s = a + b; end endmodule Fixed: module halfadd2 (c, s, a, b); output reg c, s; . Use of {sig, …, sig} input a, b; for concatenation always @(*) begin {c, s} = a + b; end endmodule 23 L07: Circuit Building Blocks I CSE369, Winter 2017 Ripple‐Carry Adder in Verilog module fulladd (cout, s, cin, a, b); output reg cout, s; input cin, a, b; always @(*) begin {cout, s} = cin + a + b; end endmodule Chain full adders? module add2 (cout, s, cin, a, b); output cout; output [1:0] s; input cin; input [1:0] a, b; wire c1; fulladder b1 (cout, s[1], c1, a[1], b[1]); fulladder b0 (c1, s[0], cin, a[0], b[0]); endmodule 24 L07: Circuit Building Blocks I CSE369, Winter 2017 Add/Sub in Verilog (parameterized) Variable‐width add/sub (with overflow, carry) module addN #(parameter N=32) (OF, CF, S, sub, A, B); output reg OF, CF; output reg [N-1:0] S; input sub; input [N-1:0] A, B; reg [N-1:0] D; // possibly flipped B always @(*) begin D = B ^ {N{sub}}; // replication operator {CF, S} = A + D + sub; OF = CF ^ S[N-1]; end endmodule . Here using OF = overflow flag, CF = carry flag • From condition flags in x86‐64 processors . {n{m}} is replication operator – repeats value m, n times 25 L07: Circuit Building Blocks I CSE369, Winter 2017 Add/Sub in Verilog (parameterized) module addN_testbench (); parameter N = 4; reg sub; reg [N-1:0] A, B; wire OF, CF; wire [N-1:0] S; addN #(.N(N)) dut (.OF, .CF, .S, .sub, .A, .B); initial begin #100; sub = 0; A = 4'b0101; B = 4'b0010; // 5 + 2 #100; sub = 0; A = 4'b1101; B = 4'b1011; // -3 + -5 #100; sub = 0; A = 4'b0101; B = 4'b0011; // 5 + 3 #100; sub = 0; A = 4'b1001; B = 4'b1110; // -7 + -2 #100; sub = 1; A = 4'b0101; B = 4'b1110; // 5 -(-2) #100; sub = 1; A = 4'b1101; B = 4'b0101; // -3 - 5 #100; sub = 1; A = 4'b0101; B = 4'b1101; // 5 -(-3) #100; sub = 1; A = 4'b1001; B = 4'b0010; // -7 - 2 #100; end endmodule 26.
Load more

Recommended publications
  • Comparison of Parallel and Pipelined CORDIC Algorithm Using RCA and CSA
    Comparison of Parallel and Pipelined CORDIC algorithm using RCA and CSA Diego Barragan´ Guerrero Lu´ıs Geraldo P. Meloni FEEC - UNICAMP FEEC - UNICAMP Campinas, Sao˜ Paulo, Brazil, 13083-852 Campinas, Sao˜ Paulo, Brazil, 13083-852 +5519 9308-9952 +5519 9778-1523 [email protected] [email protected] Abstract— This paper presents an implementation of the algorithm has two modes of operation: the rotational mode CORDIC algorithm in digital hardware using two types of (RM) where the vector (xi; yi) is rotated by an angle θ to algebraic adders: Ripple-Carry Adder (RCA) and Carry-Select obtain a new vector (x ; y ), and the vectoring mode (VM) Adder (CSA), both in parallel and pipelined architectures. Anal- N N ysis of time performance and resources utilization was carried in which the algorithm computes the modulus R and phase α out by changing the algorithm number of iterations. These results from the x-axis of the vector (x0; y0). The basic principle of demonstrate the efficiency in operating frequency of the pipelined the algorithm is shown in Figure 1. architecture with respect to the parallel architecture. Also it is shown that the use of CSA reduce the timing processing without significantly increasing the slice use. The code was synthesized us- ing FPGA development tools for the Xilinx Spartan-3E xc3s500e ' ' E N y family. N E N Index Terms— CORDIC, pipelined, parallel, RCA, CSA, y N trigonometrics functions. Rotação Pseudo-rotação R N I. INTRODUCTION E i In Digital Signal Processing with FPGA, trigonometric y i R i functions are used in many signal algorithms, for instance N synchronization and equalization [12].
    [Show full text]
  • Basics of Logic Design Arithmetic Logic Unit (ALU) Today's Lecture
    Basics of Logic Design Arithmetic Logic Unit (ALU) CPS 104 Lecture 9 Today’s Lecture • Homework #3 Assigned Due March 3 • Project Groups assigned & posted to blackboard. • Project Specification is on Web Due April 19 • Building the building blocks… Outline • Review • Digital building blocks • An Arithmetic Logic Unit (ALU) Reading Appendix B, Chapter 3 © Alvin R. Lebeck CPS 104 2 Review: Digital Design • Logic Design, Switching Circuits, Digital Logic Recall: Everything is built from transistors • A transistor is a switch • It is either on or off • On or off can represent True or False Given a bunch of bits (0 or 1)… • Is this instruction a lw or a beq? • What register do I read? • How do I add two numbers? • Need a method to reason about complex expressions © Alvin R. Lebeck CPS 104 3 Review: Boolean Functions • Boolean functions have arguments that take two values ({T,F} or {0,1}) and they return a single or a set of ({T,F} or {0,1}) value(s). • Boolean functions can always be represented by a table called a “Truth Table” • Example: F: {0,1}3 -> {0,1}2 a b c f1f2 0 0 0 0 1 0 0 1 1 1 0 1 0 1 0 0 1 1 0 0 1 0 0 1 0 1 1 0 0 1 1 1 1 1 1 © Alvin R. Lebeck CPS 104 4 Review: Boolean Functions and Expressions F(A, B, C) = (A * B) + (~A * C) ABCF 0000 0011 0100 0111 1000 1010 1101 1111 © Alvin R. Lebeck CPS 104 5 Review: Boolean Gates • Gates are electronics devices that implement simple Boolean functions Examples a a AND(a,b) OR(a,b) a NOT(a) b b a XOR(a,b) a NAND(a,b) b b a NOR(a,b) a XNOR(a,b) b b © Alvin R.
    [Show full text]
  • Digital Electronic Circuits
    DIGITAL ELECTRONIC CIRCUITS SUBJECT CODE: PEI4I103 B.Tech, Fourth Semester Prepared By Dr. Kanhu Charan Bhuyan Asst. Professor Instrumentation and Electronics Engineering COLLEGE OF ENGINEERING AND TECHNOLOGY BHUBANESWAR B.Tech (E&IE/AE&I) detail Syllabus for Admission Batch 2015-16 PEI4I103- DIGITAL ELECTRONICS University level 80% MODULE – I (12 Hours)1. Number System: Introduction to various number systems and their Conversion. Arithmetic Operation using 1’s and 2`s Compliments, Signed Binary and Floating Point Number Representation Introduction to Binary codes and their applications. (5 Hours) 2. Boolean Algebra and Logic Gates: Boolean algebra and identities, Complete Logic set, logic gates and truth tables. Universal logic gates, Algebraic Reduction and realization using logic gates (3 Hours) 3. Combinational Logic Design: Specifying the Problem, Canonical Logic Forms, Extracting Canonical Forms, EX-OR Equivalence Operations, Logic Array, K-Maps: Two, Three and Four variable K-maps, NAND and NOR Logic Implementations. (4 Hours) MODULE – II (14 Hours) 4. Logic Components: Concept of Digital Components, Binary Adders, Subtraction and Multiplication, An Equality Detector and comparator, Line Decoder, encoders, Multiplexers and De-multiplexers. (5 Hours) 5. Synchronous Sequential logic Design: sequential circuits, storage elements: Latches (SR,D), Storage elements: Flip-Flops inclusion of Master-Slave, characteristics equation and state diagram of each FFs and Conversion of Flip-Flops. Analysis of Clocked Sequential circuits and Mealy and Moore Models of Finite State Machines (6 Hours) 6. Binary Counters: Introduction, Principle and design of synchronous and asynchronous counters, Design of MOD-N counters, Ring counters. Decade counters, State Diagram of binary counters (4 hours) MODULE – III (12 hours) 7.
    [Show full text]
  • Design and Analysis of Power Efficient PTL Half Subtractor Using 120Nm Technology
    International Journal of Computer Trends and Technology (IJCTT) – volume 7 number 4– Jan 2014 Design and Analysis of Power Efficient PTL Half Subtractor Using 120nm Technology 1 2 Pranshu Sharma , Anjali Sharma 1(Department of Electronics & Communication Engineering, APG Shimla University, India) 2(Department of Electronics & Communication Engineering, APG Shimla University, India) ABSTRACT : In the designing of any VLSI System, There are a number of logic styles by which a circuit can arithmetic circuits play a vital role, subtractor circuit is be implemented some of them used in this paper are one among them. In this paper a Power efficient Half- CMOS, TG, PTL. CMOS logic styles are robust against Subtractor has been designed using the PTL technique. voltage scaling and transistor sizing and thus provide a Subtractor circuit using this technique consumes less reliable operation at low voltages and arbitrary transistor power in comparison to the CMOS and TG techniques. sizes. In CMOS style input signals are connected to The proposed Half-Subtractor circuit using the PTL transistor gates only, which facilitate the usage and technique consists of 6 NMOS and 4 PMOS. The characterization of logic cells. Due to the complementary proposed PTL Half-Subtractor is designed and simulated transistor pairs the layout of CMOS gates is not much using DSCH 3.1 and Microwind 3.1 on 120nm. The complicated and is power efficient. The large number of power estimation and simulation of layout has been done PMOS transistors used in complementary CMOS logic for the proposed PTL half-Subtractor design. Power style is one of its major disadvantages and it results in comparison on BSIM-4 and LEVEL-3 has been high input loads [3].
    [Show full text]
  • Implementation of Carry Tree Adders and Compare with RCA and CSLA
    International Journal of Emerging Engineering Research and Technology Volume 4, Issue 1, January 2016, PP 1-11 ISSN 2349-4395 (Print) & ISSN 2349-4409 (Online) Implementation of Carry Tree Adders and Compare with RCA and CSLA 1 2 G. Venkatanaga Kumar , C.H Pushpalatha Department of ECE, GONNA INSTITUTE OF TECHNOLOGY, Vishakhapatnam, India (PG Scholar) Department of ECE, GONNA INSTITUTE OF TECHNOLOGY, Vishakhapatnam, India (Associate Professor) ABSTRACT The binary adder is the critical element in most digital circuit designs including digital signal processors (DSP) and microprocessor data path units. As such, extensive research continues to be focused on improving the power delay performance of the adder. In VLSI implementations, parallel-prefix adders are known to have the best performance. Binary adders are one of the most essential logic elements within a digital system. In addition, binary adders are also helpful in units other than Arithmetic Logic Units (ALU), such as multipliers, dividers and memory addressing. Therefore, binary addition is essential that any improvement in binary addition can result in a performance boost for any computing system and, hence, help improve the performance of the entire system. Parallel-prefix adders (also known as carry-tree adders) are known to have the best performance in VLSI designs. This paper investigates three types of carry-tree adders (the Kogge- Stone, sparse Kogge-Stone, Ladner-Fischer and spanning tree adder) and compares them to the simple Ripple Carry Adder (RCA) and Carry Skip Adder (CSA). In this project Xilinx-ISE tool is used for simulation, logical verification, and further synthesizing. This algorithm is implemented in Xilinx 13.2 version and verified using Spartan 3e kit.
    [Show full text]
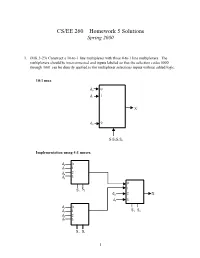
  • CS/EE 260 – Homework 5 Solutions Spring 2000
    CS/EE 260 – Homework 5 Solutions Spring 2000 1. (MK 3-23) Construct a 10-to-1 line multiplexer with three 4-to-1 line multiplexers. The multiplexers should be interconnected and inputs labeled so that the selection codes 0000 through 1001 can be directly applied to the multiplexer selections inputs without added logic. 10:1 mux d0 0 1 d1 1 X d9 9 S3S2S1S0 Implementation using 4:1 muxes. d0 0 d2 1 d4 2 d6 3 0 S 1 S2 1 d8 2 X d9 3 d 0 1 S S d3 1 3 0 d5 2 d7 3 S2 S1 1 2. (MK 3-27) Implement a binary full adder with a dual 4-to-1 line multiplexer and a single inverter. AB Ci S Co 00 0 0 0 C 0 00 1 1 i 0 01 0 1 0 C ´ C 01 1 0 i 1 i 10 0 1 0 10 1 0Ci´ 1 Ci 11 0 0 1 C 1 11 1 1 i 1 0 C 1 i 4:1 2 S 3 mux S1 S0 A B 0 0 1 4:1 Co 2 mux 1 3 S1S0 2 3. (MK 3-34) Design a combinational circuit that forms the 2-bit binary sum S1S0 of two 2-bit numbers A1A0 and B1B0 and has both input C0 and a carry output C2. Do not use half adders or full adders, but instead use a two-level circuit plus inverters for the input variables, as needed. Design the circuit by starting with the following equations for each of the two bits of the adder.
    [Show full text]
  • UNIT 8B a Full Adder
    UNIT 8B Computer Organization: Levels of Abstraction 15110 Principles of Computing, 1 Carnegie Mellon University - CORTINA A Full Adder C ABCin Cout S in 0 0 0 A 0 0 1 0 1 0 B 0 1 1 1 0 0 1 0 1 C S out 1 1 0 1 1 1 15110 Principles of Computing, 2 Carnegie Mellon University - CORTINA 1 A Full Adder C ABCin Cout S in 0 0 0 0 0 A 0 0 1 0 1 0 1 0 0 1 B 0 1 1 1 0 1 0 0 0 1 1 0 1 1 0 C S out 1 1 0 1 0 1 1 1 1 1 ⊕ ⊕ S = A B Cin ⊕ ∧ ∨ ∧ Cout = ((A B) C) (A B) 15110 Principles of Computing, 3 Carnegie Mellon University - CORTINA Full Adder (FA) AB 1-bit Cout Full Cin Adder S 15110 Principles of Computing, 4 Carnegie Mellon University - CORTINA 2 Another Full Adder (FA) http://students.cs.tamu.edu/wanglei/csce350/handout/lab6.html AB 1-bit Cout Full Cin Adder S 15110 Principles of Computing, 5 Carnegie Mellon University - CORTINA 8-bit Full Adder A7 B7 A2 B2 A1 B1 A0 B0 1-bit 1-bit 1-bit 1-bit ... Cout Full Full Full Full Cin Adder Adder Adder Adder S7 S2 S1 S0 AB 8 ⁄ ⁄ 8 C 8-bit C out FA in ⁄ 8 S 15110 Principles of Computing, 6 Carnegie Mellon University - CORTINA 3 Multiplexer (MUX) • A multiplexer chooses between a set of inputs. D1 D 2 MUX F D3 D ABF 4 0 0 D1 AB 0 1 D2 1 0 D3 1 1 D4 http://www.cise.ufl.edu/~mssz/CompOrg/CDAintro.html 15110 Principles of Computing, 7 Carnegie Mellon University - CORTINA Arithmetic Logic Unit (ALU) OP 1OP 0 Carry In & OP OP 0 OP 1 F 0 0 A ∧ B 0 1 A ∨ B 1 0 A 1 1 A + B http://cs-alb-pc3.massey.ac.nz/notes/59304/l4.html 15110 Principles of Computing, 8 Carnegie Mellon University - CORTINA 4 Flip Flop • A flip flop is a sequential circuit that is able to maintain (save) a state.
    [Show full text]
  • Design of Adder / Subtractor Circuits Based On
    ISSN (Print) : 2320 – 3765 ISSN (Online): 2278 – 8875 International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering (An ISO 3297: 2007 Certified Organization) Vol. 2, Issue 8, August 2013 DESIGN OF ADDER / SUBTRACTOR CIRCUITS BASED ON REVERSIBLE GATES V.Kamalakannan1, Shilpakala.V2, Ravi.H.N3 Lecturer, Department of ECE, R.L.Jalappa Institute of Technology, Doddaballapur, Karnataka, India 1 Asst. Professor & HOD, Department of ECE, R.L.Jalappa Institute of Technology, Doddaballapur, Karnataka, India2 Lab Assistant, Dept. of ECE, U.V.C.E, Bangalore Karnataka, India3 ABSTRACT: Reversible logic has extensive applications in quantum computing, it is a unconventional form of computing where the computational process is reversible, i.e., time-invertible. The main motivation behind the study of this technology is aimed at implementing reversible computing where they offer what is predicted to be the only potential way to improve the energy efficiency of computers beyond von Neumann-Landauer limit. It is relatively new and emerging area in the field of computing that taught us to think physically about computation Quantum Computing will be a total change in how the computer will operate and function. The reversible arithmetic circuits are efficient in terms of number of reversible gates, garbage output and quantum cost. In this paper design Reversible Binary Adder- Subtractor- Mux, Adder-Subtractor- TR Gate., Adder-Subtractor- Hybrid are proposed. In all the three design approaches, the Adder and Subtractor are realized in a single unit as compared to only full adder/subtractor in the existing design. The performance analysis is verified using number reversible gates, Garbage input/outputs and Quantum Cost.The reversible 4-bit full adder/ subtractor design unit is compared with conventional ripple carry adder, carry look ahead adder, carry skip adder, Manchester carry adder based on their performance with respect to area, timing and power.
    [Show full text]
  • Area and Power Optimized D-Flip Flop and Subtractor
    IT in Industry, Vol. 9, No.1, 2021 Published Online 28-02-2021 AREA AND POWER OPTIMIZED D-FLIP FLOP AND SUBTRACTOR T. Subhashini1, M. Kamaraju2, K. Babulu3 1,2 Department of ECE, Gudlavalleru Engineering College, India 3Department of ECE, UCOE, JNTUK, Kakinada, India Abstract: Low power is essential in today’s technology. It LITERATURE SURVEY is most significant with high speed, small size and stability. So, power reduction is most important in modern In the era of microelectronics, power dissipation is technology using VLSI design techniques. Today most of limiting factor. In any CMOS technology, provides the market necessities require low power, long run time very low Static power dissipation. Due to the and market which also deserve small size and high speed. discharge of capacitance, during the switching In this paper several logic circuits DFF with 5 transistors operation, that cause a power dissipation. Which and sub tractor circuit using powerless XOR gate and increases with the clock frequency. Using Groundless XNOR gates are implemented. In the proposed Transmission Gate Technique Such unnecessary DFF, the area can be decreased by 62% & substarctor discharging can be prevented. Due to the resistance of circuit, area decreased by 80% and power consumption of switches, impartial losses may be occurred for any DFF and subtractor circuit are 15.4µW and 13.76µW logic operation. respectively, but these are very less as compared to existing techniques. To avoid these minor losses keep clock frequency to be small than the technological limit. There are Keyword: D FF, NMOS, PMOS, VLSI, P-XOR, G-XNOR different types of Transmission Gate logic families.
    [Show full text]
  • Design of High Speed and Low Power Six Transistor Full Adder Using Two Transistor Xor Gate
    International Journal of Electronics, Communication & Instrumentation Engineering Research and Development (IJECIERD) ISSN 2249-684X Vol. 3, Issue 1, Mar 2013, 87-96 © TJPRC Pvt. Ltd. DESIGN OF HIGH SPEED AND LOW POWER SIX TRANSISTOR FULL ADDER USING TWO TRANSISTOR XOR GATE B. DILLI KUMAR, K. CHARAN KUMAR & T. NAVEEN KUMAR M. Tech (VLSI), Department of ECE, Sree Vidyanikethan Engineering College (Autonomous), Tirupati, India ABSTRACT Full adder is one of the major components in the design of many sophisticated hardware circuits. In this paper the full adder has been designed by using a new efficient design with less number of transistors. A 2 transistor XOR gate has been proposed with the help of two PMOS (Positive Metal Oxide Semiconductor) transistors. By using this 2T XOR gate the size of the full adder has been decreased to a large extent which can be implemented with only 6 transistors. The proposed full adder has a significant improvement in silicon area and power delay product when compared to the previous 8T full adder circuits. Further the proposed adder requires less area to perform a required logic function. Further, the proposed full adder has less power dissipation which makes it suitable for many of the low power applications and because of less area requirement the proposed design can be used in many of the portable applications also . KEYWORDS: Full Adder, XOR, Less Area, Speed, Low Power, Delay, Less Transistor Count, Low Power VLSI INTRODUCTION Full adder is one of the basic building blocks of many of the digital VLSI circuits. Several refinements has been made regarding its structure since its invention.
    [Show full text]
  • High Performance Full Subtractor Using Floating-Gate MOSFET
    Microelectronic Engineering 162 (2016) 75–78 Contents lists available at ScienceDirect Microelectronic Engineering journal homepage: www.elsevier.com/locate/mee Accelerated publication High performance full subtractor using floating-gate MOSFET Roshani Gupta, Rockey Gupta, Susheel Sharma Department of Physics and Electronics, University of Jammu, Jammu 180006, India article info abstract Article history: Low power consumption has become one of the primary requirements in the design of digital VLSI circuits in re- Received 18 March 2016 cent years. With scaling down of device dimensions, the supply voltage also needs to be scaled down for reliable Received in revised form 10 May 2016 operation. The speed of conventional digital integrated circuits is degrading on reducing the supply voltage for a Accepted 11 May 2016 given technology. Moreover, the threshold voltage of MOSFET does not scale down proportionally with its di- Available online 13 May 2016 mensions, thus putting a limitation on its suitability for low voltage operation. Therefore, there is a need to ex- Keywords: plore new methodology for the design of digital circuits well suited for low voltage operation and low power Full subtractor consumption. Floating-gate MOS (FGMOS) technology is one of the design techniques with its attractive features FGMOS of reduced circuit complexity and threshold voltage programmability. It can be operated below the conventional TG threshold voltage of MOSFET leading to wider output signal swing at low supply voltage and dissipates less CPL power as compared to CMOS circuits without much compromise on the device performance. This paper presents GDI the design of full subtractor using FGMOS technique whose performance has been compared with full subtractor Power delay product circuits employing CMOS, transmission gates (TG), complementary pass transistor logic (CPL) and gate diffusion input (GDI).
    [Show full text]
  • Design and Implementation of Adder/Subtractor and Multiplication Units for Floating-Point Arithmetic
    International Journal of Electronics Engineering, 2(1), 2010, pp. 197-203 Design and Implementation of Adder/Subtractor and Multiplication Units for Floating-Point Arithmetic Dhiraj Sangwan1 & Mahesh K. Yadav2 1MITS University, Laxmangarh, Rajasthan, India 2BRCM College of Engg. & Tech., Bahal, M D University, Rohtak, Haryana, India Abstract: Computers were originally built as fast, reliable and accurate computing machines. It does not matter how large computers get, one of their main tasks will be to always perform computation. Most of these computations need real numbers as an essential category in any real world calculations. Real numbers are not finite; therefore no finite, representation method is capable of representing all real numbers, even within a small range. Thus, most real values will have to be represented in an approximate manner. The scope of this paper includes study and implementation of Adder/Subtractor and multiplication functional units using HDL for computing arithmetic operations and functions suited for hardware implementation. The algorithms are coded in VHDL and validated through extensive simulation. These are structured so that they provide the required performance i.e. speed and gate count. This VHDL code is then synthesized by Synopsys tool to generate the gate level net list that can be implemented on the FPGA using Xilinx FPGA Compiler. Keywords: Algorithm, ALU, Adder/Subtractor, Arithmetic Computation, Floating Point, IEEE 754 Standard, Multiplication, RTL, Significand, Simulation, Synthesis, VHDL. 1. INTRODUCTION normalized floating-point numbers as if they were The Arithmetic logic unit or ALU is the brain of the computer, integers)[9]. the device that performs the arithmetic operations like addition and subtraction or logical operations like AND and 1.2.
    [Show full text]